техники и Дальнейшее изложение понятий дискриминантного анализа мы будем иллюстрировать примерами из психолого-педагогического изучения, одной из задач которого была классификация преподавателей на группы.
Для исполнения этого изучения были организованы две группы испытуемых. Первую группу, названную «рядовые» составили педагоги, чьи опытные показатели не превышали среднего уровня (85 человек). Во вторую, названную «элита» (45 человек), вошли педагоги, каковые, согласно точки зрения специалистов, были лучшими представителями собственной профессии (отметим, что ДА относится к задачам группировки испытуемых на заданные группы либо, что то же самое, к методам распознавания образов «с преподавателем»).
В следствии тестирования испытуемых было получено более 40 показателей (переменных)[1], характеризующих каждого из них. Задача пребывала в выработке решающего правила (уравнения) для отнесения каждого испытуемого к собственной группе (классу). В ДА предполагается, что в случае, если процент верных классификаций окажется высоким, то это значит, что «преподаватель» справился со своей задачей, и мы можем пользоваться отысканным уравнением для классификации малоизвестных испытуемых.
Ответственным есть вопрос, все ли переменные, обрисовывающие испытуемых, необходимо включать в обработку посредством ДА? направляться иметь в виду, что переменные, каковые не дают значимых межгрупповых различий, из ДА направляться исключить. В отечественном примере для определения переменных, подлежащих исключению, было совершено сравнение групп по каждой переменной посредством t-критерия Стьюдента. Оказалось, что статистически значимо группы различаются лишь по 8 из более чем 40 переменных. Конкретно к этим переменным и была применена процедура ДА.
Процедуру и технику ДА будем обсуждать в соответствии с последовательными этапами реализации компьютерной программы ДА в пакете STATGRAF .
Процедуры интерпретации
Первый вопрос, что направляться обсудить, связан с способами интерпретации. Задача интерпретации связана с определением значимости и числа канонических дискриминантных функцийи с выяснением их значений для объяснения различий между классами.
Каноническая дискриминантная функция есть линейной комбинацией дискриминантных переменных. Ее уравнение, именуемое дискриминантным, имеет следующий вид:
Fkm = U0+U1X1km+U2X2km+ … +UpXikm
где Fkm – значение канонической дискриминантной функции для m-го объекта в группе K; Xikm – значение дискриминантной переменной Xi для m-го объекта в группе K; Ui – коэффициенты, снабжающие исполнение требуемых условий.
Коэффициенты для Fkm подбираются так, дабы ее средние значения для разных классов как возможно больше отличались друг от друга.
STATGRAF рассчитывает стандартизированные и нестандартизованные коэффициенты канонической дискриминантной функции. Отличие между ними содержится в следующем: нестандартизованные коэффициенты – в отличие от стандартизованных – рассчитываются на основании матрицы, содержащей исходные значения наблюдений, каковые не приведены к стандартной форме.
Нестандартизованные коэффициенты канонической дискриминантной функции нужны для определения положения наблюдений (объектов) в дискриминантом пространстве (табл. 4.1).
Таблица 4.1
Нестандартизованные коэффициенты канонической дискриминантной
функции
| В | М | Q1 | Q4 | АSОл | МРСл | 0-D | E-D | Const. |
| 0,03 | 0,16 | 0,04 | 0,14 | 0,01 | 0,24 | 0,23 | -0,18 | -3,5 |
Конкретно они являются коэффициентами при переменных в дискриминантном уравнении
F = 0,03´В + 0,16´Мк + 0,04´Q1 + 0,14´Q4 + 0,01´ASOл 4 + 0,2´МРСл + 0,23´OD — 0,17´ED — 3,5
Значение функции интерпретируется как координата объекта (преподавателя) в пространстве данной функции. Пространство канонической дискрининантной функции задается совокупностью объектов наблюдения, в отечественной случае это координаты 130 преподавателей (85 рядовых — гр. I и 45 элитных — гр. 2).
Значение дискриминантной функции измеряется в единицах стандартного отклонения, другими словами значение F для данного преподавателя воображает число стандартных отклонений точки от главного центроида либо, иначе говоря положение точки на оси, где нулевая точка — основной центроид.
Центроид — это мнимая точка, координаты которой имеется среднее значение переменных в данной группе. Основной центроид – это точка пространства, в которой все дискриминантные переменные принимают средние (по всем наблюдениям) значения. Иначе говоря это центральное положение всех точек, воображающих наблюдения. При графическом изображении дискриминантных функций в главном центроиде помещается начало координат, поскольку в этом случае разглядываемые объекты и группы соотносятся с центром совокупности.
У нас имеется две группы — значит — два центроида: Ц1 = -0,43, Ц2 = +0,81 (эти значения кроме этого рассчитываются программой ДА STATGRAFа). Центроиды возможно применять для изучения различий между группами, поскольку они занимают положение обычных представителей соответствующей группы.
Число канонических дискриминантных функций не может быть больше числа групп минус 1. Значит при наличии двух групп вероятна лишь одна функция. При таких условиях точки, соответствующие объектам, находятся на протяжении некоей прямой.
Возможно выстроить график-гистограмму распределения объектов довольно данной оси. Как пример мы нанесли на график значения канонической дискриминантной функции для 10 первых участников из каждой группы (рис. 1).
Расположив групповые гистограммы одну над второй, легко сравнивать относительное положение групп. График говорит о том, что группы в полной мере различимы. Центроиды отлично отделимы друг от друга.
По значению канонической дискриминатной функции, вычисленной для конкретного человека, возможно сделать заключение о том, как типично положение данного человека среди участников группы. Возможность эта появляется по причине того, что дискриминантные значения выражены в единицах стандартного отклонения, другими словами имеют единый масштаб. К примеру, значения канонической дискриминантной функции для преподавателей с условными номерами 86, 89 и 92 равны соответственно 1,8; 0,7 и -0,3. № 89 находится рядом с центроидом группы (Ц2 = +0,  и может принимать во внимание обычным ее представителем. № 86 и № 92 отклоняются от собственного центроида более чем на стандартное отклонение. Как мы знаем, что в пределах стандартного отклонения лежит 68% всех наблюдений, значит № 89 и № 92 входят в оставшиеся 32%, другими словами находятся на границах собственной группы.
и может принимать во внимание обычным ее представителем. № 86 и № 92 отклоняются от собственного центроида более чем на стандартное отклонение. Как мы знаем, что в пределах стандартного отклонения лежит 68% всех наблюдений, значит № 89 и № 92 входят в оставшиеся 32%, другими словами находятся на границах собственной группы.
Рис. 4.1 Распределение значений канонической дискриминантной функции для десяти произвольно забранных участников из каждой группы. Ось абсцисс есть канонической дискриминантной функцией, измеренной в единицах стандартного отклонения.
+ ++
++ ++ + + +
Гр.1 (рядовые) —* * * * *
-1 ц1 0 ц2 +1
-0,43 0,81
++
+ + +++ ++ +
Гр.2 (элита) —* * * * * * *
-1 ц1 0 ц2 +1
-0,43 -03 0,81 1,8
Стандартизованные коэффициенты показывают вклад переменной в значение функции. Их полезно использовать для обнаружения тех переменных, каковые означают больше вторых для чёрта изучаемой области действительности. Полная величина коэффициента анализируется в стандартной форме: чем она больше, тем больше вклад данной переменной. Для отечественной функции велик вклад переменной 0D, после этого по убывающей следуют шкалы ED, Мк, МРСл, Q4, Q1, В, asoл. Данный ранжир показывает на особенную значимость для профессии педагога изюминок поведения в конфликтных обстановках, каковые измеряются шкалами 0D и ED из методики Розенцвейга. Причем, значимость переменной ОД (большой вклад) в 8,3 раза превосходит значимость переменной ASOл (минимальный вклад).
Таблица 4.2
Стандартизованные коэффициенты канонической дискриминантной функции
| B | M | Q1 | Q4 | ASOл | MPCл | O-D | E-D |
| 0.09 | 0.34 | 0.11 | 0.28 | 0.06 | 0.29 | 0.5 | -0.39 |
Процедуры классификации
Следующий вопрос, что мы обсудим, знакомясь с дискриминантным анализом, связан с способами классификации.
Классификация – это особенный вид деятельности исследователя, в котором или дискриминантные переменные, или канонические дискриминантные функции употребляются для предсказания класса, к которому более возможно в собственности некий объект. Существует пара процедур классификации, но все они сравнивают положение объекта с каждым из центроидов классов, требуют определения понятия «расстояния» между каждым центроидом и объектом группы, дабы возможно было приписать объект к «ближайшей» группе. Классификация проводится посредством линейной комбинации дискриминантных переменных. Ищется такая комбинация, которая максимизирует различия между группами, но минимизирует дисперсию в групп. Особенная линейная комбинация для каждой группы именуется классифицирующая функция[2]. Она имеет форму:
Нк = Вк0 +Вк1Х1 + Вк2 Х2 +… + Вкn Хn
Где Нк – значение функции для группы К, а Вк – коэффициенты несложной классифицирующей функции. STATGRAF (и все другие компьютерные программы ДА) рассчитывают эти коэффициенты. В нашем случае имеется две группы, значит две классифицирующие функции:
Таблица 4.3
Коэффициенты несложной классифицирующей функции
| В | МК | Q1 | Q4 | ASOЛ | МРСл | OD | ED | const | |
| Н1 | 0.2 | 0.7 | 0.36 | 1.2 | 0.37 | 5.54 | 1.68 | 3.1 | 47.6 |
| Н2 | 0.24 | 0.88 | 0.41 | 1.33 | 0.36 | 5.83 | 1.97 | 2.84 | 52.16 |
HI = 0,2´В + 0,7´МК + 0,36´Q1 + 1,2´Q4 — 0,37´ASOл +5,54´МРСл +
+ 1,68´OD + 3,1´ED — 47,6
Н2 = 0,24´В + 0,88´МК + 0,41´Q1 + 1,33´Q4 — 0,36´АSОл +
+ 5,83´МРСл +1,97´00 + 2,84´ED — 52,16
Классификация производится следующим образом: подсчитываются значения HI и Н2; объект относится к той группе, у которой значения Н больше.
Совершим для примера классификацию трех человек из элитной группы под условными номерами 1, 2, 3.
Таблица 4.4
| № 1 | № 2 | № 3 | |
| HI | 42,9 | 35,8 | |
| H2 | 37,1 |
У всех трех значение Н2 больше, значит их направляться отнести к элитной группе. Тут мы продемонстрировали, как трудится функция, классифицируя известных преподавателей (тех, принадлежность которых к одной из групп известна заблаговременно). Именно на этих преподавателях строилась классифицирующая функция, происходило обучение совокупности. Сейчас в уравнения возможно подставлять значения переменных малоизвестных людей (к примеру, абитуриентов) и относить их к возможно успешным либо к таким, у кого потенциал успешности под вопросом.
Обобщенную меру «расстояния» между каждым центроидом и объектом группы внес предложение индийский статистик Махаланобис – расстояние Махаланобиса D2, по окончании вычисления которого для каждого класса объект классифицируется в группу с мельчайшим D2. Это класс, чей обычный профиль по дискриминантным переменным больше похож на профиль этого объекта. В случае, если расстояние до ближайшего класса громадно, то согласие между профилями будет нехорошим, но если сравнивать с любым вторым классом – хорошим.
Оказалось, что статистика D2 владеет теми же особенностями, что и статистика c2. Расстояние, так, измеряется в «c2-единицах». Исходя из этого, в соответствии с закономерностями c2-распределения, мы можем ожидать, что большая часть объектов будет группироваться вблизи центроида, и их плотность будет убывать по мере удаления от центроида. Зная расстояние от центроида, возможно сообщить, какая часть класса находится ближе к центроиду, а какая – дальше от него. Следовательно, возможно оценить возможность того, что объект, так-то удаленный от центроида, принадлежит к классу. Эта возможность рассчитывается компьютерными программами ДА.
К классификации в большинстве случаев обращаются как к средству предсказания принадлежности к группе малоизвестных объектов, но возможно применять ее кроме этого для проверки точности процедуры классификации. Для этого берутся узнаваемые объекты и к ним используются правила классификации.
Часть верно классифицированных объектов говорит о точности процедуры и косвенно подтверждает степень разделения классов. Итог описывается в классификационной матрице.
Таблица 4.5
Итоговая классификация
| «обучающая» несколько | Верный прогноз | Ошибочный прогноз | всего | |||
| частота | процент | частота | процент | частота | процент | |
| 76,47 | 23,53 | |||||
| 73,33 | 26,67 |
В первой группе всего 85 человек. Из них классифицировано верно (отнесено к первой группе) 65 человек либо 76 %, неправильно (отнесено ко второй группе) 20 человек, другими словами допущено 24% неточностей. Подобно из 45 человек второй группы правильно классифицировано 33 человека либо 73%.
Всего правильно классифицировано 65 + 33 = 98 человек из 130. Так, точность предсказания равна 98:130 = 0,75 либо 75% Процентное содержание как мера точности предсказания считается самая подходящей мерой дискриминантной информации.
ТЕМА 5.МАТЕМАТИКО-СТАТИСТИЧЕСКИЙ СПОСОБ
КЛАССИФИКАЦИИ В ПСИХОЛОГИИ:
ВАРИАНТЫ МОДЕЛИ КЛАСТЕРНОГО АНАЛИЗА
Назначение
Кластерный анализ решает задачу построения классификации, другими словами разделения исходного множества объектов на группы (классы, кластеры). Наряду с этим предполагается, что у исследователя нет исходных допущений ни о составе классов, ни об их отличии друг от друга. Приступая к кластерному анализу, исследователь располагает только информацией о чертях (показателях) для объектов, разрешающей делать выводы о сходстве (различии) объектов, или лишь данными об их попарном сходстве (различии). В литературе довольно часто видятся синонимы кластерного анализа: автоматическая классификация, таксономический анализ, анализ образов (без обучения).
Не обращая внимания на то, что кластерный анализ известен довольно в далеком прошлом, распространение эта rpyппаметодов взяла значительно позднее, чем другие многомерные способы, такие, как факторный анализ. Только по окончании публикации книги «Начала численной таксономии» биологами Р. Сокэл и П. Снит в первой половине 60-ых годов XX века начинают оказаться первые изучения с применением этого способа. Однако, до сих пор в психологии известны только единичные случаи успешного применения кластерного анализа, не обращая внимания на его необыкновенную простоту. Приводит к удивлению настойчивость, с которой психологи применяют для ответа несложной задачи классификации (объектов, показателей) таковой сложный способ, как факторный анализ. Вместе с тем кластерный анализ не только значительно несложнее и нагляднее решает эту задачу, но и имеет несомненное преимущество: итог его применения не связан с утратой кроме того части исходной информации о различиях объектов либо корреляции показателей.
Варианты кластерного анализа – это множество несложных вычислительных процедур, применяемых для классификации объектов. Классификация объектов – это группирование их в классы так, дабы объекты в каждом классе были более похожи, чем на объекты из вторых классов. Более совершенно верно, кластерный анализ– это процедура упорядочивания объектов в относительно однородные классы на базе попарного сравнения этих объектов по предварительно определенным и измеренным параметрам.
Существует множество вариантов кластерного анализа, но самый активно применяются способы, объединенные неспециализированным заглавием иерархический кластерный анализ{Hierarchical Cluster Analysis). В будущем под кластерным анализом мы будем подразумевать конкретно эту группу способов. Разглядим фундаментальной принцип иерархического кластерного анализа на примере.
Пример
Предположим, 10 студентам внесли предложение оценить совершённое с ними занятие по двум параметрам: увлекательность (Pref) и полезность (Use). Для оценки употреблялась 10-балльная шкала. Полученные эти (2 переменные для 10 студентов – табл. 5.1) легко представить в виде графика двумерного рассеивания (рис. 5.1).
Таблица 5.1
| Pref | ||||||||||
| Use |
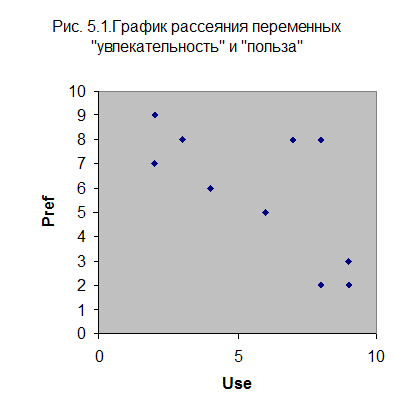
Само собой разумеется, классификация объектов по итогам измерения всего двух переменных не требует применения кластерного анализа: группировки и без того возможно выделить методом визуального анализа. Так, в этом случае наблюдаются четыре группировки: 9, 2, 3 –- занятие нужное, но не увлекательное; 1, 10, 8 – занятие увлекательное, но ненужное; 5,7 – занятие и нужное и увлекательное; 4, 6 – занятие умеренно увлекательное и умеренно нужное. Кроме того для трех переменных возможно обойтись и без кластерного анализа, поскольку компьютерные программы разрешают строить трехмерные графики. Но для 4 и более переменных визуальный анализ данных фактически неосуществим. Однако, неспециализированный принцип классификации объектов при помощи кластерного анализа не зависит от количества измеренных показателей, поскольку яркой информацией для этого способа являются различия между классифицируемыми объектами.
Кластерный анализ объектов, для которых заданы значения количественных показателей начинается с расчета различий для всех пар объектов. В качестве меры различия выбирается расстояние между объектами в P-мерном пространстве показателей, значительно чаще – евклидово расстояние либо его квадрат. В этом случае Р= 2 и евклидово расстояние между объектами i и j определяется формулой:
dv= (xl -xj)2+(yl -yj)2 ,
где х – это значения одного, а у – другого показателя.
На первом шаге кластерного анализа методом перебора всех пар объектов определяется пара (либо пары) самый родных объектов, каковые объединяются в первичные кластеры. Потом на каждом шаге к каждому первичному кластеру присоединяется объект (кластер), что к нему ближе. Данный процесс повторяется , пока все объекты не будут объединены в один кластер. Критерий объединения объектов (кластеров) возможно различным и определяется способом кластерного анализа. Главным результатом применения иерархического кластерного анализа есть дендрограмма – графическое изображение последовательности объединения объектов в кластеры. Для данного примера дендрограмма приведена на рис.2
C A S E 0 5 10 15 20 25
Label Num +———+———+———+———+———+
3 oo
9 oooooooooooooooooooooooooooooooooooooooooooooooooo
2 o? o
8 ouoo o
10 o? uoooooooooooooooooo o
1 ooo? uooooooooooooooooooooooooooo?
5 ouoooooooooooo o
7 o? uooooooo?
4 ooooouooooooo?
6 ooooo?
Рис 5. 2. Дендрограмма для 10 студентов (способ средней связи)
На дендрограмме номера объектов следуют по вертикали. По горизонтали отмечены расстояния (в условных единицах), на которых происходит объединение объектов в кластеры. На первых шагах происходит образование кластеров: (3,9, 2) и (5,7). Потом образуется кластер (8,10, 1) – расстояния между этими объектами больше, чем между теми, каковые были объединены на прошлых шагах. Следующий кластер – (4, 6). Потом в один кластер объединяются кластеры (5, 7) и (4, 6), и т. д. Процесс заканчивается объединением всех объектов в один кластер. Количество кластеров определяет по дендрограмме сам исследователь. Так, если судить по дендрограмме, в этом случае возможно выделить три либо четыре кластера.
Как видно из примера, кластерный анализ – это комбинаторная процедура, имеющая несложный и наглядный итог. Широта вероятного применения кластерного анализа очевидна так же, как очевиден и его суть. Классифицирование либо разделение исходного множества объектов на различающиеся группы – в любой момент первый ход в любой умственной деятельности, предваряющий поиск обстоятельств найденных различий.
Возможно указать последовательность задач, при ответе которых кластерный анализ есть более действенным, чем другие многомерные способы:
§ разбиение совокупности испытуемых на группы по измеренным показателям с целью предстоящей проверки обстоятельств межгрупповых различий по внешним параметрам, к примеру, проверка догадок о том, проявляются ли типологические различия между испытуемыми по измеренным показателям;
§ использование кластерного анализа как намного более несложного и наглядного аналога факторного анализа, в то время, когда ставится лишь задача группировки показателей на базе их корреляции;
§ классификация объектов на базе ярких оценок различий между ними (к примеру, изучение социальной структуры коллектива согласно данным социометрии – по распознанным межличностным предпочтениям).
Не обращая внимания на различие целей проведения кластерного анализа, возможно выделить неспециализированную его последовательность как последовательность довольно независимых шагов, играющих значительную роль в прикладном изучении:
1. Отбор объектов для кластеризации. Объектами смогут быть, в зависимости от цели изучения: а) испытуемые; б) объекты, каковые оцениваются испытуемыми; в) показатели, измеренные на выборке испытуемых.
2. Определение множества переменных, по которым будут различаться объекты кластеризации. Для испытуемых – это комплект измеренных показателей, для оцениваемых объектов – субъекты оценки, для показателей – испытуемые. В случае, если в качестве данных предполагается использовать результаты попарного сравнения объектов, нужно четко выяснить критерии этого сравнения испытуемыми (специалистами).
3. Определение меры различия между объектами кластеризации. Это первая неприятность, которая есть специфичной для способов анализа различий: многомерного шкалирования и кластерного анализа. Используемые требования и меры различия к ним детально обсуждаются в теме, посвященной многомерному шкалированию.
4. применение и Выбор способа классификации для групп сходных объектов. Это вторая и центральная неприятность кластерного анализа. Ее весомость связана с тем, что различные способы кластеризации порождают различные группировки для одних и тех же данных. Не смотря на то, что анализ и содержится в обнаружении структуры, на деле в ходе кластеризации структура привносится в эти, и эта привнесенная структура может не совпадать с настоящей.
5. Проверка достоверности разбиения на классы.
Последний этап не всегда нужен, к примеру, при обнаружении социальной структуры группы. Однако, направляться не забывать, что кластерный анализ постоянно разобьёт совокупность объектов на классы, независимо от того, существуют ли они в действительности. Исходя из этого безтолку обосновывать существенность разбиения на классы, к примеру, на основании достоверности различий между классами по показателям, включенным в анализ. В большинстве случаев контролируют устойчивость группировки – на повторной аналогичной выборке объектов. Значимость разбиения контролируют по внешним параметрам – показателям, не вошедшим в анализ.
Способы кластерного анализа
Яркими данными для применения любого способа кластеризации есть матрица различий между всеми парами объектов. Определение либо задание меры различия есть первым и нужным шагом кластерного анализа.
Из всего множества способов кластеризации самый распространены так именуемые иерархические агломеративные способы. Наименование показывает на то, что классификация осуществляется методом последовательного объединения (агломерации) объектов в группы, выясняющиеся в следствии иерархически орга-низованными. Эти способы – весьма простые комбинаторные процедуры, отличающиеся критерием объединения объектов в кластеры.
Критерий объединения многократно используется ко всей матрице попарных расстояний между объектами. На первых шагах объединяются самый родные объекты, находящиеся на одном уровне сходства. После этого поочередно присоединяются остальные объекты, пока все они не объединятся в один громадный кластер. Итог работы способа представляется графически в виде дендрограммы– ветвистого древовидного графика.
Существуют разные способы иерархического кластерного анализа, например, в программе SPSS предлагается 7 способов. Любой способ дает собственные результаты кластеризации, но три из них являются самые типичными. Исходя из этого разглядим результаты применения этих способов к одним и тем же данным из отечественного примера.
Способ одиночной связи(Single Linkage) – самый понятный способ, что довольно часто именуют способом «ближайшего соседа» (Nearest Neighbor). Метод начинается с поиска двух самый родных объектов, пара которых образует первичный кластер. Любой последующий объект присоединяется к тому кластеру, к одному из объектов которого он ближе.
На рис 3. приведен итог применения способа. Сопоставляя эту ден-дрограмму с рис. 1, возможно подметить, что объект 4 присоединяется к кластеру (8, 10, 1) и на том же расстоянии – к объекту 6 в связи с тем, что расстояние от объекта 4 до объекта 6 такое же, что и до объекта 1.
C A S E 0 5 10 15 20 25
Label Num +———+———+———+———+———+
3 oo
9 oooooooooooooooooooooooooooooooooooooooooooooooooo
2 o? o
5 ouoooooooooooooooooooooooooooooooooooo o
7 o? o o
8 oooooo uooooooooooo?
10 ooooouoooooooooooo o
1 ooooo? uooooooooooooooooooo?
4 ooooooooooooooooou
6 ooooooooooooooooo?
Рис 5. 3. Дендрограмма для 10 студентов (способ одиночной связи)
Из рисунка видно, что способ имеет тенденцию к образованию долгих кластеров «цепочного» вида. Так, способ имеет тенденцию образовывать маленькое число больших кластеров. К изюминкам способа возможно отнести да и то, что результаты его применения довольно часто не дают возможности выяснить, как много кластеров находится в данных.
Способ полной связи(Complete Linkage) довольно часто именуют способом «дальнего соседа» (Furthest Neighbor). Правило объединения этого способа подразумевает, что новый объект присоединяется к тому кластеру, самый далекий элемент которого находится ближе к новому объекту, чем самые далекие элементы вторых кластеров. Это правило есть противоположным прошлому и более твёрдым. Исходя из этого тут отмечается тенденция к выделению большего числа компактных кластеров, складывающихся из самые похожих элементов.
Сравним итог применения способа полной связи (рис. 19.4), способа одиночной связи (рис. 19.3) и фактическую конфигурацию объектов (рис. 19.2). Различия в работе способов проявляются в первую очередь в отношении объектов 4 и 6. Способ полной связи объединяет их в отдельный кластер и соединяет с кластером (5, 7) раньше, чем с кластером (8, 10, 1) – в отличие от способа одиночной связи.
C A S E 0 5 10 15 20 25
Label Num +———+———+———+———+———+
3 oo
9 oooooooooooooooooooooooooooooooooooooooooooooooooo
2 o? o
5 ouoooooooooooooooooooooooooooooooooooo o
7 o? o o
8 oooooo uooooooooooo?
10 ooooouoooooooooooo o
1 ooooo? uooooooooooooooooooo?
4 ooooooooooooooooou
6 ooooooooooooooooo?
Рис. 5. 4. Дендрограмма для 10 студентов (способ полной связи)
Объект 4 присоединяется сперва к объекту 6, в силу того, что данный последний к нему ближе, чем самый дальний объект кластера (8, 10,1). На этом же основании кластер (4, 6) присоединяется к кластеру (5, 7), в силу того, что самый дальний объект 6 кластера (4, 6) ближе к самому дальнему объекту 7 кластера (5, 7), чем к самому дальнему объекту 8 кластера (8, 10, 1).
Способ средней связи(Average Linkage) либо межгрупповой связи {Between Groups Linkage) занимает промежуточное положение относительно крайностей способов одиночной и полной связи. На каждом шаге вычисляется среднее арифметическое расстояние между каждым объектом из одного кластера и каждым объектом из другого кластера. Объект присоединяется к данному кластеру, в случае, если это среднее расстояние меньше, чем среднее расстояние до любого другого кластера. По собственному принципу данный способ обязан давать более правильные результаты классификации, чем остальные способы. То, что объединение кластеров в способе средней связи происходит при расстоянии большем, чем в способе одиночной связи, но меньшем, чем в способе полной связи, и растолковывает промежуточное положение этого способа. Итог применения способа изображен на рис.2. Потому, что объектов в отечественном примере мало, результаты применения способов полной и средней связи различаются незначительно.
В настоящих изучениях в большинстве случаев имеются десятки классифицируемых объектов, и использование каждого из указанных способов дает значительно различные результаты для одних и тех же данных. литературные данные и Опыт свидетельствуют, что самый близкий к настоящей группировке итог дает возможность приобрести способ средней связи. Но это не свидетельствует бесполезность применения двух вторых способов. Способ одиночной связи «сжимает» пространство, образуя предельное количество громадных кластеров. Способ полной связи «расширяет» пространство, образуя предельное количество компактных кластеров. Любой из трех способов привносит в настоящее соотношение объектов собственную структуру и представляет собой как бы собственную точку зрения на действительность. Исследователь, в зависимости от стоящей перед ним задачи, вправе выбрать тот способ, что ему больше подходит.
Численность классовявляется отдельной проблемой в кластерном анализе. Сложность содержится в том, что не существует формальных параметров разрешающих выяснить оптимальное число классов. В конечном счете это определяется самим исследователем исходя из содержательных мыслей. Но для предварительного определения числа классов исследователь может обратиться к таблице последовательности агломерации {Agglomeration schedule). Эта таблица разрешает проследить динамику повышения различий по шагам кластеризации и выяснить ход, на котором отмечается резкое возрастание различий. Оптимальному числу классов соответствует разность между числом объектов и порядкового номера шага, на котором найден перепад различий. Более детально порядок оценки численности классов рассмотрен на примере компьютерной обработки.