Задачадинамического программирования – многошаговый процесс принятия ответов. На каждом шаге определяется экстремум функции лишь одной переменной.
Задача о распределении капитальных вложений. Указано n пунктов, где требуется выстроить либо реконструировать предприятия одной отрасли, для чего выделено b рублей. – прирост мощности на i-том предприятии, если оно возьмёт капитальных вложений. Требуется отыскать распределение
Максимизирующее суммарный прирост мощности/прибыли.
Данные:
Таблица 1.Данные
Формулировка задачи:
Производственное объединение состоит их четырех фирм (n=4). Общая сумма капитальных вложений образовывает 700 тыс. руб. (b=700), выделяемые фирмам суммы кратны 100 тыс. руб. Значения функций приведены в таблице 1. К примеру, число 49 в первой строке свидетельствует, что в случае, если третье предприятие возьмёт 600 тыс. руб., капитальных вложений, то прирост прибыли на этом предприятии составит 49 тыс. руб. и т.д.
Отыскать таковой вариант распределения средств капитальных вложений, дабы прирост прибыли был велик.
Математическая модель задачи
Примем следующие обозначения:
- n – количество пунктов, где требуется выстроить либо реконструировать предприятия одной отрасли;
- b – общая сумма выделенных средств;
- – количество капитальных вложений, взятых i-тым предприятием;
- – прирост мощности прибыли на i-том предприятии, если оно возьмёт i-e предприятие;
- – прирост мощности (прибыли)
Требуется отыскать такое распределение капитальных вложений между фирмами, которое максимизирует прирост мощности либо прибыли:
(1.1.)
при ограничении по неспециализированной сумме капитальных вложений
,
наряду с этим будем вычислять, что все переменные принимают лишь целые неотрицательные значения.
Ответ
Введем параметр состояния – количество средств, выделяемых нескольким фирмам, и определим функцию состояния – большую прибыль на первых k фирмах, если они совместно приобретают руб.
В случае, если из рублей k-е предприятие возьмёт рублей, то каково бы ни было это значение, оставшиеся ( рублей направляться распределить между фирмами от первого до k-го так, дабы была взята большая прибыль . Тогда прибыль k фирм будет равна . Необходимо выбрать такое значение между 0 и дабы эта сумма была большой, и мы переходим к рекуррентному соотношению:
для k = 2, 3, 4, …, n. В случае, если же k = 1, то .
Первым этапом ответа задачи есть составление таблицы 2. Значения складываются со значениями и на каждой северо-западной диагонали отмечается большое значение:
Таблица 2.Второе предприятие
| 20* | |||||||||
| 33* | |||||||||
| 45* | |||||||||
| 57* | |||||||||
| 67* | |||||||||
| 75* | |||||||||
| 81* | |||||||||
Отмеченными значениями заполняется таблица 3 и указываются соответствующие значения :
Таблица 3.Второе предприятие
Следующий этап – табулирование функции , (таблица 4) и составление таблицы 5:
Таблица 4.Третье предприятие
| 20* | 33* | 45* | 57* | 67* | 75* | ||||
| 81* | |||||||||
Таблица 5.Третье предприятие
В таблице 6 заполняется лишь диагональ для значения . Большое значение на данной диагонали следовательно четвертому предприятию должно быть выделено
200 тыс. руб.
Таблица 6. Четвертое предприятие
| 103* | |||||||||
На долю остальных фирм остается 700 – 200 = 500 тыс. руб. В соответствии с таблице 5 третьему предприятию должно быть выделено:
0 тыс. руб.
Подобно находим значение для второго предприятия:
тыс.руб.
На долю первого предприятия остается:
тыс. руб.
Так, наилучшим есть следующее распределение капитальных вложений по фирмам:
.
Большой прирост прибыли составит (в соответствии с таблице 1):
тыс. руб.
10. Оптимизация замысла распределения ресурсов между производственными подразделениями посредством двойственных оценок при двухуровневой совокупности управления.
Данные:
В – количество ресурсов:
А – нормы затрат на единицу продукции каждого вида:
С – удельная прибыль по каждому виду продукции:
Формулировка задачи:
Предприятие имеет три филиала, любой из которых создаёт по два вида продукции, требующей одних и тех же видов ресурсов. Любая фабрика располагает двумя видами ресурсов (матрицы , суммарные количества которых равны 242 ед. и 185 ед. соответственно.
Известны нормы затрат для каждого вида продукции раздельно по филиалам (матрицы ), и удельная прибыль по каждому виду продукции по филиалам (матрицы ).
Требуется перераспределить ресурсы между филиалами так, дабы суммарная прибыль по предприятию была большой.
Модель задачи:
Найтивекторы (распределение ресурсов между филиалами) и оптимальный замысел:
)
Максимизирующий целевые функции:
Соответственно, и суммарную прибыль L , при следующих ограничениях:
`
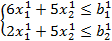
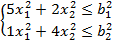
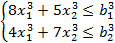И при условии неотриательности переменных:
Ответ задачи:
Составляем локальные задачи:
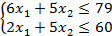(4.1.) 
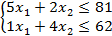(4.2.) 
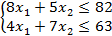` (4.3.)
Ответ задач (4.1.) – (4.3.) посредством Excel:
Таблица 4.1. Ответ локальной задачи (1)
| Изделия | Изд1 | Изд2 | Целевая функция/количество продаж |
| Цена за единицу | |||
| Замысел выпуска |
Двойственные оценки
Таблица 4.2.Ответ локальной задачи (2)
| Изделия | Изд1 | Изд2 | Целевая функция/количество продаж |
| Цена за единицу | |||
| Замысел выпуска | 13,4 | 720,4 |
Двойственные оценки:
Таблица 4.3.Ответ локальный задачи (3)
| Изделия | Изд1 | Изд2 | Целевая функция/количество продаж |
| Цена за единицу | |||
| Замысел выпуска | 5,25 | 433,5 |
Двойственные оценки
Взяты следующие оптимальные замыслы по филиалам:
Большие доходы по каждому филиалу:
Неспециализированная прибыль по предприятию:
Двойственные оценки по фирмам:
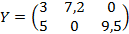
Отличие между двойственными оценками:
- Для первой пары филиалов образовывает 9,2 ед.;
- Для второй пары филиалов образовывает 16,7 ед.
Отличие для второй пары максимально, следовательно, второй и третий филиалы выбираются для перераспределения.
Модель объединенной задачи (задача (2) + задача (3)):
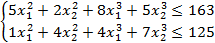(4.4.)
Ответ задачи (4.4.) в Excel
Таблица 4.4. Ответ объединенной задачи (4.4.) (2) +(3)
| Изделия | Изд1 | Изд2 | Изд3 | Изд4 | Целевая функция |
| Цена за единицу | |||||
| Замысел выпуска | 18,6 | 11,2 | 1344,4 |
Двойственные оценки:
Получено ответ:
Переменная , что свидетельствует, что первое изделие в третьем филиале производить не нужно.
Двойственные оценки для объединенной задачи:
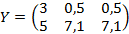
Распределение ресурсов принимает следующие значения:
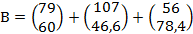
Количество ресурсов в первом филиале остается неизменным.
Прибыль по всему предприятию увеличилась и образовывает L = 1344,5 + 550 = 1894,5 д. ед.
Следующий этап – распределение ресурсов между первым и вторым филиалами, для которых отличие между двойственными оценками образовывает 4,6. Объединенная задача для этих филиалов будет иметь вид:
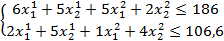(4.5.)
Ответ задачи (4.5.) в Excel
Таблица 4.5. Ответ объединенной задачи (4.5.) (1) +(2)
| Изделия | Изд1 | Изд2 | Изд3 | Изд4 | Целевая функция |
| Цена за единицу | |||||
| Замысел выпуска | 25,04 | 18,39 | 1666,082 |
Двойственные оценки
Получено ответ:
Переменные что свидетельствует, что в первом филиал производить продукцию второго вида не нужно.
Двойственные оценки для объединенной задачи:
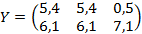
Отличие между двойственными оценками между вторым и третьим предприятием образовывает 4,9.
Распределение ресурсов принимает следующий вид:
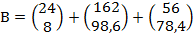
Количество ресурсов в третьем филиале остается неизменным.
Прибыль по всему предприятию увеличилась и образовывает L = 1666,08 + 436,8 = 2103,6д. ед..
Согласно решению двух объединенных задач, неспециализированная прибыль по предприятию возросла на 399,6 единиц. Выполняя последовательные шаги оптимизации, мы будем увеличивать суммарную прибыль ход за шагом. Процесс длится , пока двойственные оценки задачи не станут приблизительно однообразными.
11. Использование способа динамического программирования для оптимального управления производством и запасами.
В лекциях не было!!! Давал слово не давать!
12. Модель рентабельных размеров заказываемых партий (модель ЭВРП). Формула Уилсона, характеристическое свойство оптимального размера партии.
В лекциях не было!!! Давал слово не давать!
13. Задача формирования оптимального портфеля ценных бумаг. Математическая модель задачи, её анализ и решение.
В лекциях не было!!! Давал слово не давать!