Сборник содержит две контрольных работы для студентов-заочников 1 курса всех направлений, по которым ведется обучение в Волгодонском инженерно-техническом университете — филиале НИЯУ МИФИ. Эти контрольные работы охватывают все разделы, представленные в федеральных национальных образовательных стандартах, и составлены в соответствии с соответствующими рабочими и унифицированными планами программами подготовки бакалавров всех направлений филиала.
Предусмотрен следующий порядок исполнения контрольных работ:
| Семестр | I | II |
| Номера контрольных работ |
Выбор варианта производится по последней цифре номера зачетной книжки.
Контрольная работа № 1.
Элементы линейной аналитической геометрии и алгебры. производная и Предел функции одной переменной.
Задание 1.Дана совокупность линейных уравнений
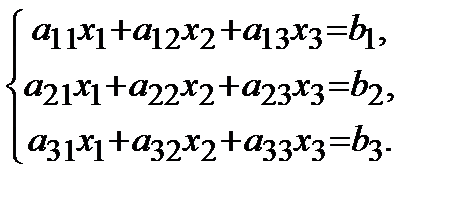
Решить двумя методами: 1) способом Крамера; 2) способом матричного исчисления.
| 1. | 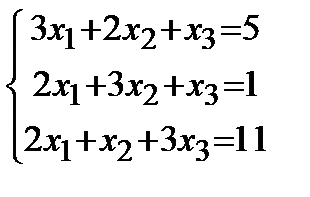
|
2. | 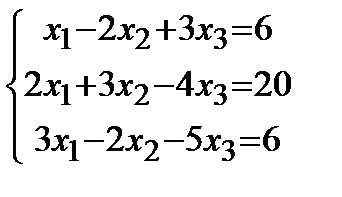
|
| 3. | 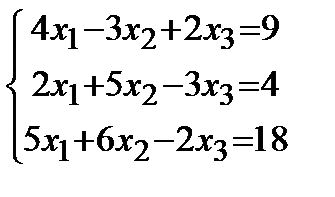
|
4. | 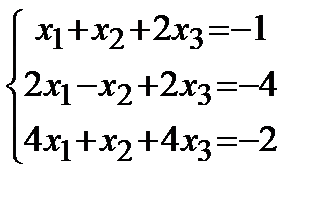
|
| 5. | 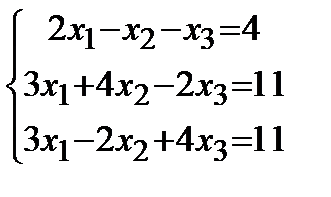
|
6. | 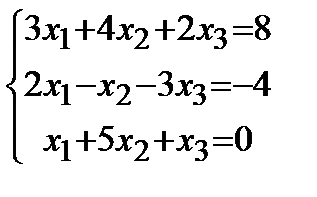
|
| 7. | 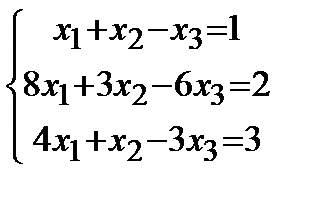
|
8. | 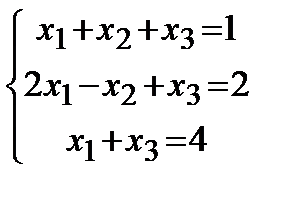
|
| 9. | 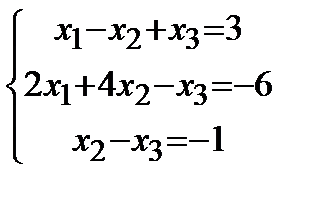
|
10. | 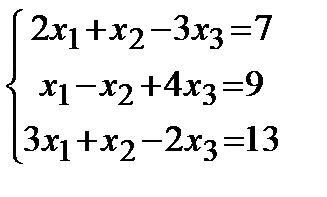
|
Задание 2.Даны координаты вершин пирамиды 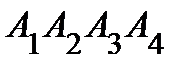 . Отыскать:
. Отыскать:
1) длину ребра 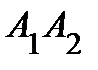 ;
;
2) угол между ребрами 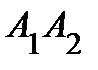 и
и 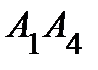 ;
;
3) площадь грани 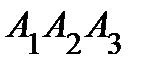 ;
;
4) количество пирамиды 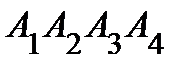 ;
;
5) уравнение прямой 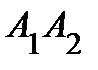 ;
;
6) уравнение плоскости 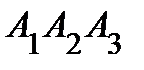 ;
;
| Вариант | 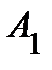
|
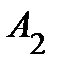
|
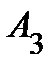
|
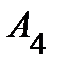
|
| 1. | 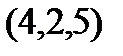
|
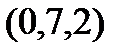
|
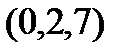
|
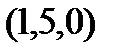
|
| 2. | 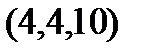
|
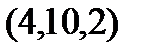
|
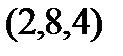
|
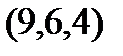
|
| 3. | 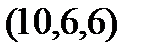
|
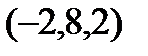
|
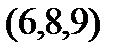
|
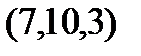
|
| 4. | 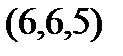
|
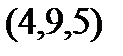
|
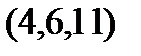
|
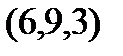
|
| 5. | 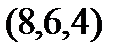
|
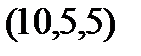
|
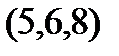
|
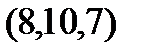
|
| 6. | 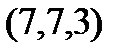
|
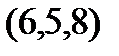
|
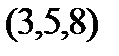
|
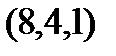
|
| 7. | 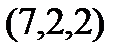
|
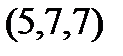
|
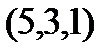
|
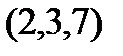
|
| 8. | 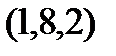
|
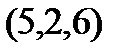
|
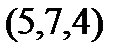
|
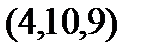
|
| 9. | 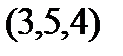
|
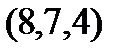
|
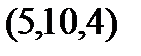
|
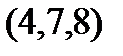
|
| 10. | 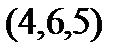
|
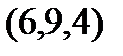
|
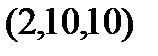
|
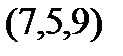
|
Задание 3.Отыскать пределы функций, не пользуясь правилом Лопиталя.
БИБЛИОГРАФИЧЕСКИЙ ПЕРЕЧЕНЬ.
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Т.2.-M.: Наука, 1985.- 560с.
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1976.- 200с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Т.1.-M.: Наука, 1985.- 456с.
4. Бермант А.Ф., Араманович И.Г. Краткий курс матанализа для втузов — СПб.: Изд-во “Лань”, 2003. – 736c.
Контрольная работа № 2.
Приложение производной. Интегралы.
Задание 1.Вычислить пределы по правилу Лопиталя.
1.a) 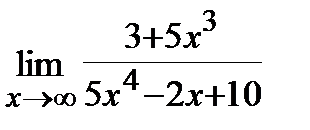 , б)
, б) 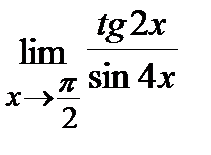 .
.
2. a) 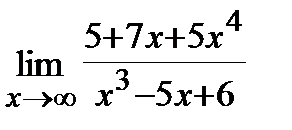 , б)
, б) 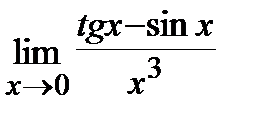 .
.
3. a) 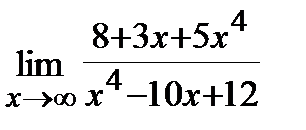 , б)
, б) 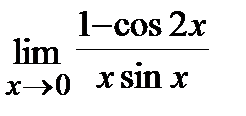 .
.
4. a) 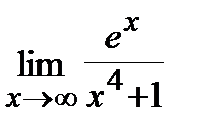 , б)
, б) 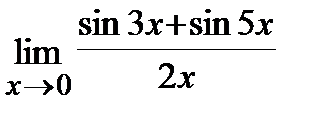 .
.
5. a) 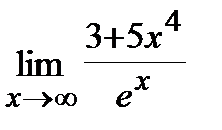 , б)
, б) 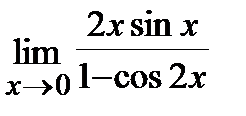 .
.
6. a) 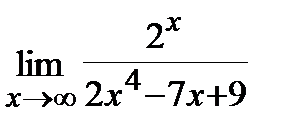 , б)
, б) 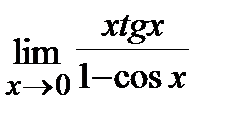 .
.
7. a) 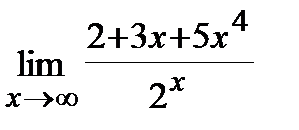 , б)
, б) 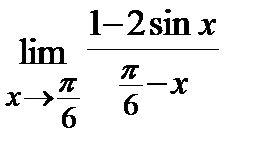 .
.
8. a) 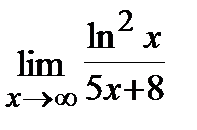 , б)
, б) 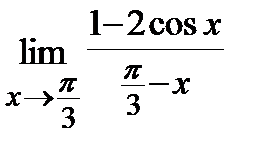 .
.
9. a) 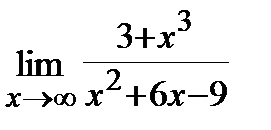 , б)
, б) 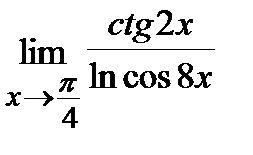 .
.
10. a) 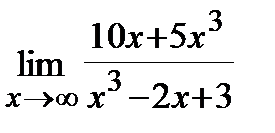 , б)
, б) 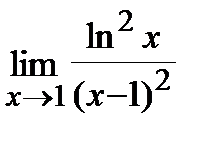 .
.
Задание 2.Отыскать громаднейшее и мельчайшее значения функции 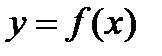 на отрезке
на отрезке 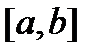 .
.
1. 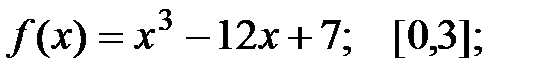
2. 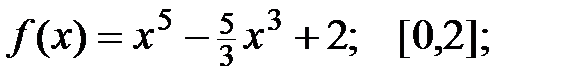
3. 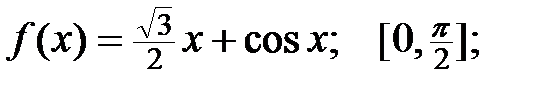
4. 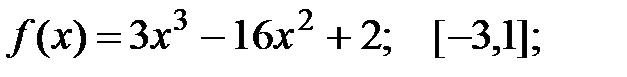
5. 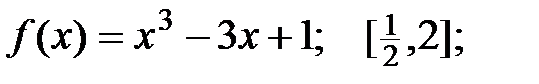
6. 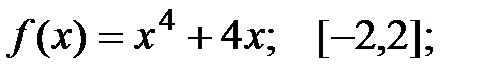
7. 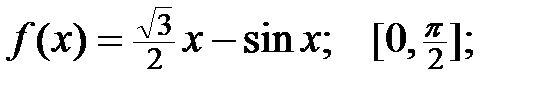
8. 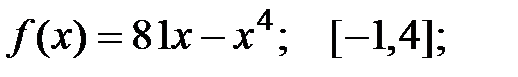
9. 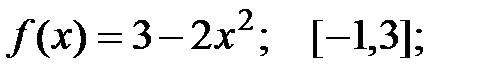
10. 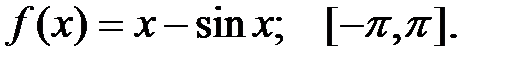
Задание 3.Изучить способами дифференциального исчисления функцию 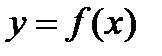 и, применяя результаты изучения, выстроить ее график.
и, применяя результаты изучения, выстроить ее график.
| 1. | 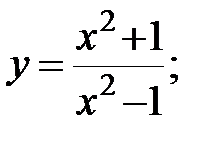
|
2. | 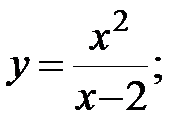
|
| 3. | 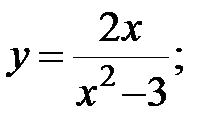
|
4. | 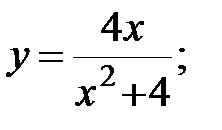
|
| 5. | 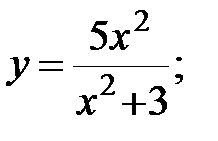
|
6. | 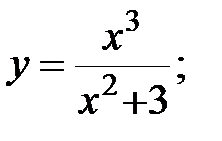
|
| 7. | 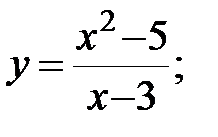
|
8. | 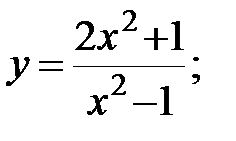
|
| 9. | 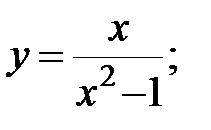
|
10. | 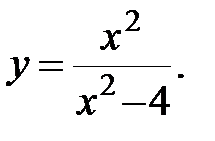
|
Задание 4.Вычислить неизвестные интегралы.
Задание 5.Вычислить площадь фигуры, ограниченной линиями, заданными в декартовых координатах. Сделать чертеж.
| 1. | 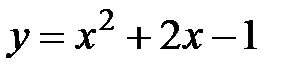 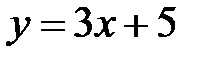
|
2. | 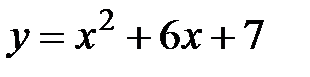 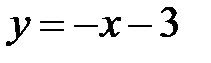
|
| 3. | 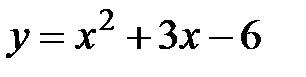 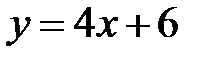
|
4. | 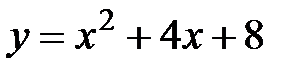 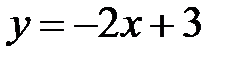
|
| 5. |
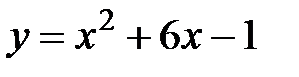 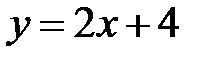
|
6. | 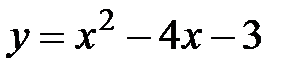 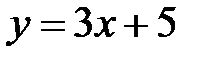
|
| 7. | 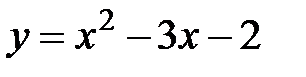 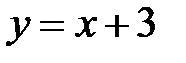
|
8. | 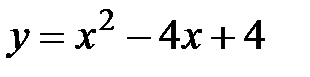 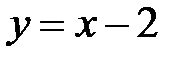
|
| 9. | 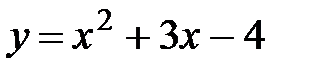 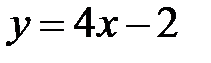
|
10. | 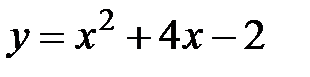 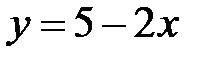
|
БИБЛИОГРАФИЧЕСКИЙ ПЕРЕЧЕНЬ.
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Т.1.-M.: Наука, 1985.- 456с.
2. Бермант А.Ф., Араманович И.Г. Краткий курс матанализа для втузов — СПб.: Изд-во “Лань”, 2003. – 736c.
Методические указания к исполнению контрольной их №1
приложения и работы Матрицы
Матрицей размера 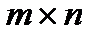 именуется прямоугольная таблица чисел
именуется прямоугольная таблица чисел
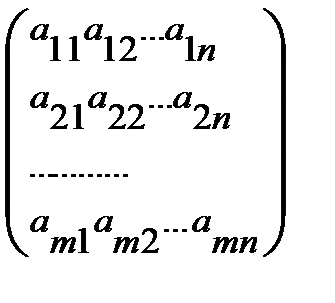 ,
,
имеющая 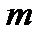 строчков (однообразной длины) и
строчков (однообразной длины) и 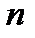 (однообразной длины) столбцов.
(однообразной длины) столбцов.
Элементы 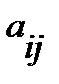 матрицы снабжаются двумя индексами, первый из которых обозначает номер строчка, второй — номер столбца, на пересечении которых стоит элемент
матрицы снабжаются двумя индексами, первый из которых обозначает номер строчка, второй — номер столбца, на пересечении которых стоит элемент 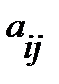 . В случае, если матрица имеет
. В случае, если матрица имеет 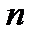 столбцов и
столбцов и 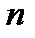 строк, то матрицу именуют квадратной.
строк, то матрицу именуют квадратной.
Матрицы однообразного размера возможно складывать. Наряду с этим суммой матриц 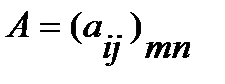 и
и 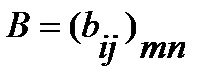 именуют матрицу
именуют матрицу 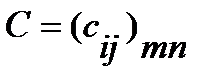 , для которой
, для которой 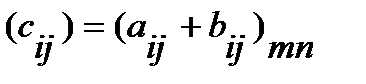 .
.
К примеру,
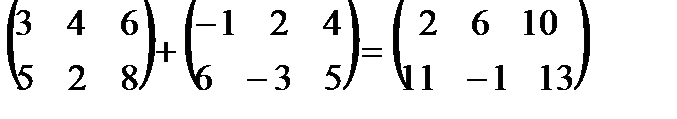 .
.
Произведением матрицы 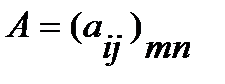 на число
на число 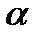 именуют матрицу
именуют матрицу 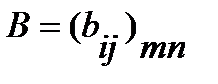 , любой элемент которой
, любой элемент которой 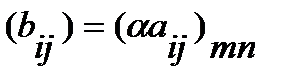 . К примеру,
. К примеру,
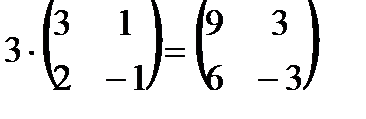 .
.
Задача. Даны матрицы 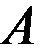 и
и 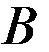 :
:
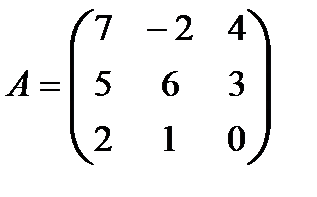 ;
; 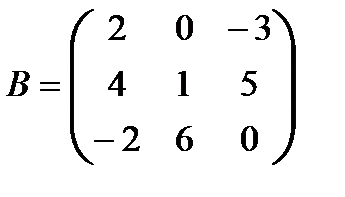 .
.
Отыскать матрицы: a) 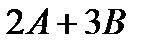 , б)
, б) 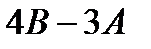 .
.
Ответ. а) 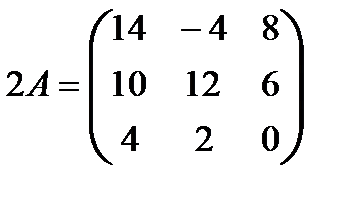 ;
; 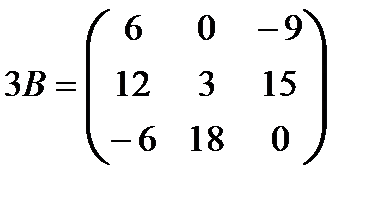 ;
;
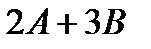
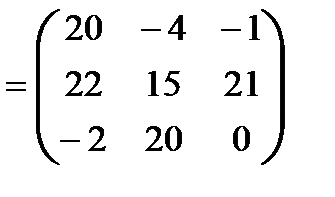 ;
;
б) 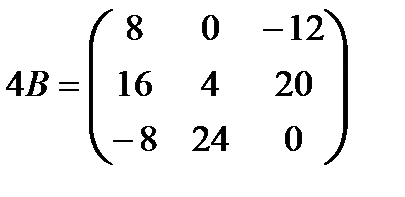 ;
; 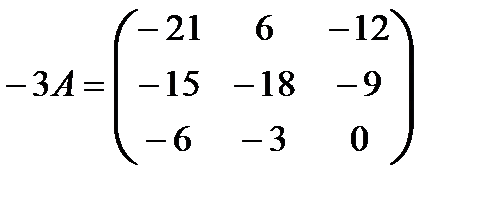 ;
;
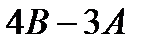
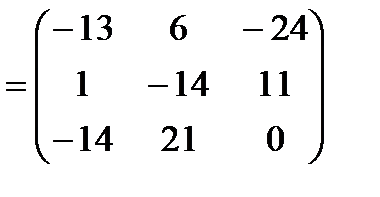 ;
;
Произведением 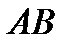 матрицы
матрицы 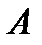 размером
размером 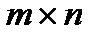 на матрицу
на матрицу 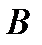 размером
размером 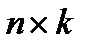 именуют матрицу C размером
именуют матрицу C размером 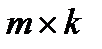 , любой элемент которой
, любой элемент которой
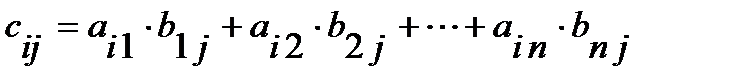 , где
, где 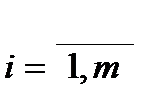 ;
; 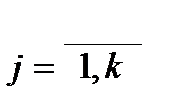 .
.
Другими словами элемент – ой строки и 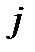 – го столбца матрицы произведения
– го столбца матрицы произведения 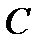 равен сумме произведений элементов – ой строки матрицы
равен сумме произведений элементов – ой строки матрицы 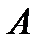 на соответствующие элементы
на соответствующие элементы 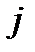 – го столбца матрицы
– го столбца матрицы 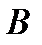 .
.
В случае, если выяснено произведение 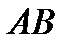 ,то это не означает, что выяснено произведение
,то это не означает, что выяснено произведение 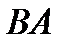 . Это произведение может не иметь смысла. В случае, если выполняется
. Это произведение может не иметь смысла. В случае, если выполняется 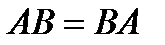 , то матрицы именуются перестановочными, либо коммутирующими. Отметим сразу же, что в большинстве случаев
, то матрицы именуются перестановочными, либо коммутирующими. Отметим сразу же, что в большинстве случаев 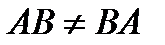 .
.
Задача. Даны матрицы 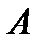 и
и 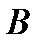 :
:
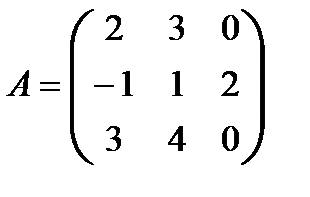 ;
; 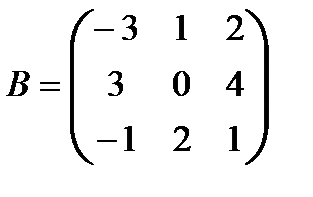 .
.
Отыскать матрицу 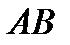 .
.
Ответ.
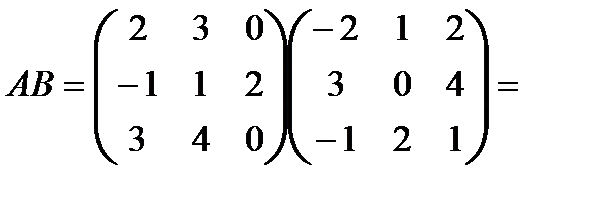
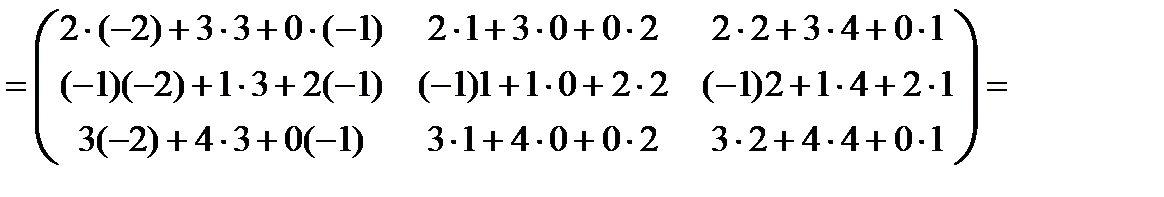
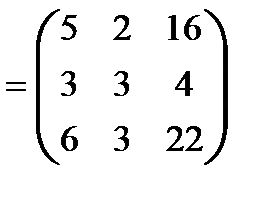 .
.
.
Обратные матрицы
Квадратная матрица 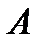 именуется обратимой, в случае, если существует матрица такая, что
именуется обратимой, в случае, если существует матрица такая, что 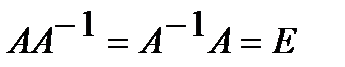 . Эту матрицу именуют обратной к матрице
. Эту матрицу именуют обратной к матрице 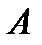 и обозначают
и обозначают 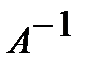 .
.
Каждой квадратной матрице 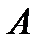 соответствует определитель
соответствует определитель 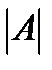 . Оказывается, что в случае, если
. Оказывается, что в случае, если 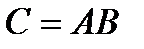 , то
, то 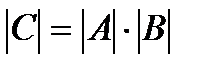 . Так как
. Так как 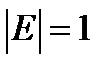 , то
, то 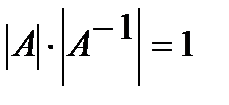 .
.
Нужным и достаточным условием существования обратной матрицы есть условие 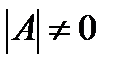 .
.
Алгебраическим дополнением 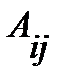 элемента
элемента 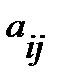 именуется произведение числа
именуется произведение числа 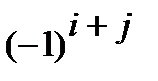 на определитель, получающийся при вычеркиванием -ой строки и
на определитель, получающийся при вычеркиванием -ой строки и 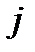 -го столбца. К примеру, определитель
-го столбца. К примеру, определитель
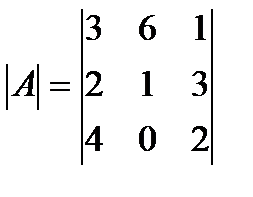
имеет следующие алгебраические дополнения:
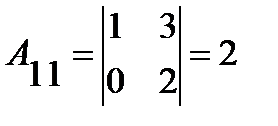 ;
; 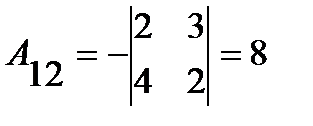 ;
; 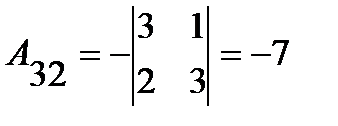 ;
; 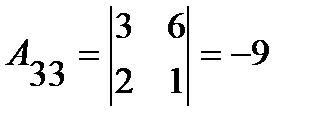 .
.
В случае, если определитель матрицы 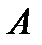 отличен от нуля
отличен от нуля 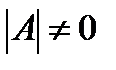 , то обратную матрицу строят следующим образом:
, то обратную матрицу строят следующим образом:
1) находят все алгебраические дополнения;
2) составляют матрицу алгебраических дополнений 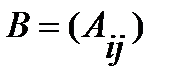 ;
;
3) транспонируют матрицу B и умножают на число 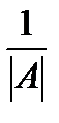 .
.
Полученная матрица 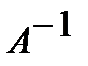 и будет обратной матрицей.
и будет обратной матрицей.
Задача. Решить матричным методом совокупность уравнений
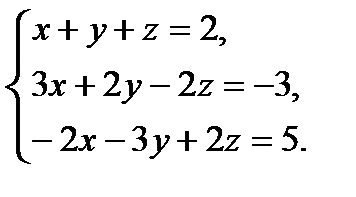
Ответ. Допустим, что
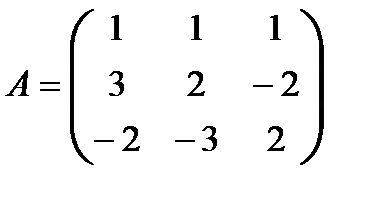 ;
; 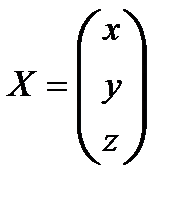 ;
; 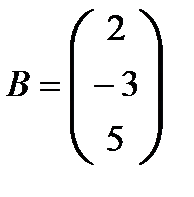 .
.
Тогда матричная запись разглядываемой совокупности уравнений будет иметь вид
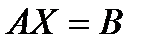 . (10)
. (10)
Отыщем определитель 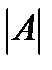 матрицы
матрицы 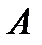 :
:
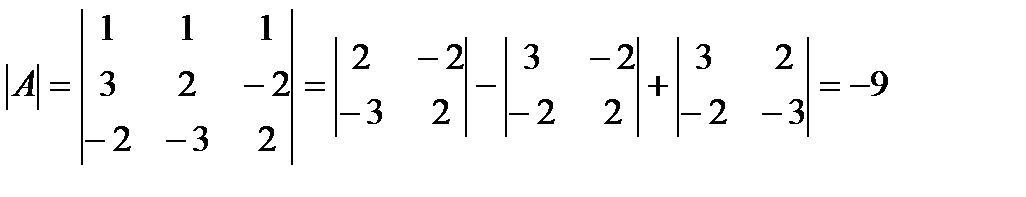 .
.
Так как 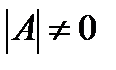 , то существует обратная матрица
, то существует обратная матрица 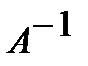 . Умножая слева на матрицу
. Умножая слева на матрицу 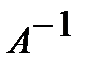 равенство (10), возьмём, что
равенство (10), возьмём, что 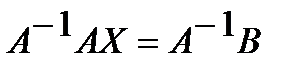 либо
либо 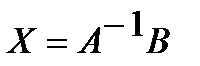 . Отыщем обратную матрицу
. Отыщем обратную матрицу 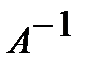 :
:
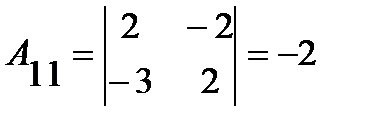 ;
; 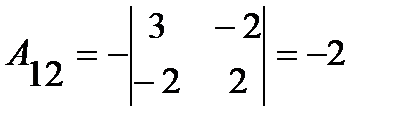 ;
; 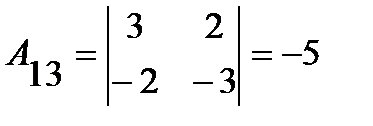 ;
;
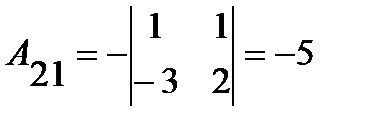 ;
; 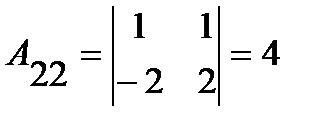 ;
; 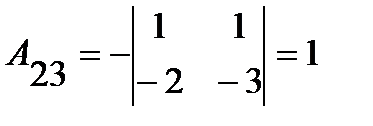 ;
;
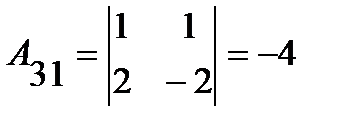 ;
; 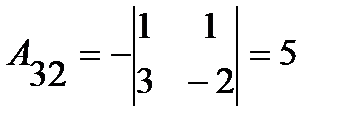 ;
; 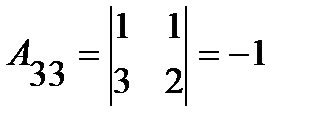 .
.
Обратная матрица 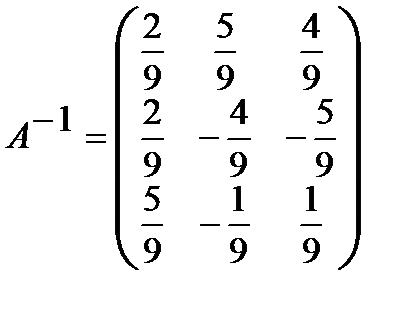 .
.
Но тогда 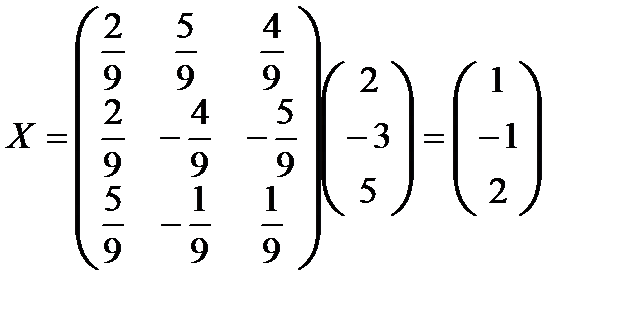 .
.
Ответ: 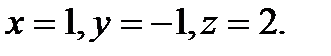
Элементы векторной алгебры
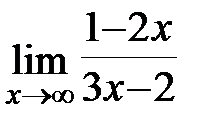 ; б)
; б) 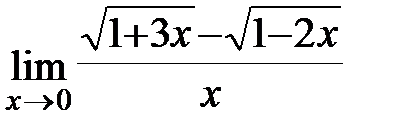 ; в)
; в) 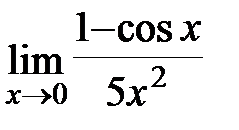 ; г)
; г) 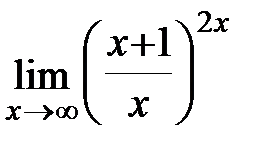 .
. 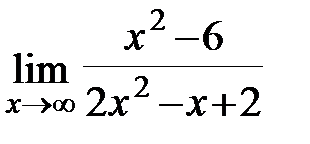 ; б)
; б) 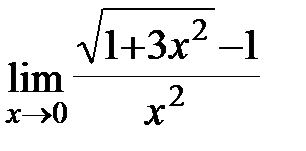 ; в)
; в) 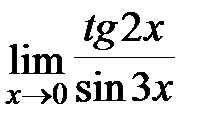 ; г)
; г) 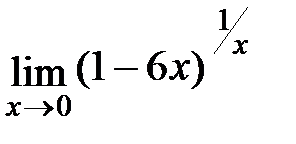 .
. 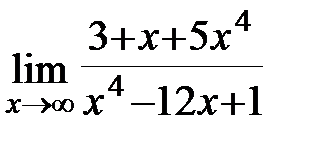 ;б)
;б) 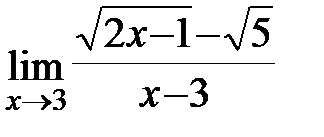 ;
; 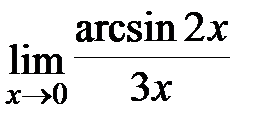 ; г)
; г) 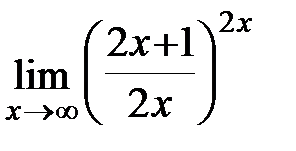 .
. 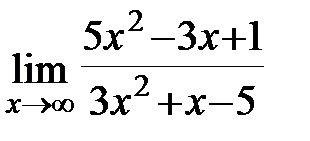 ;б)
;б) 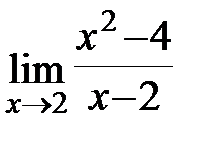 ; в)
; в) 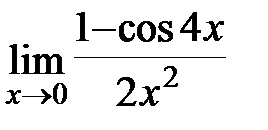 ; г)
; г) 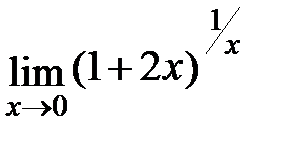 .
. 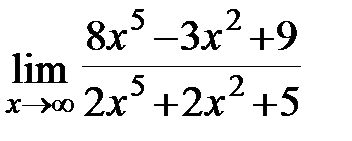 ;б)
;б) 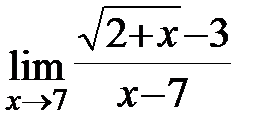 ; в)
; в) 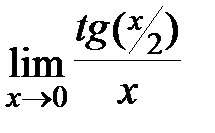 ; г)
; г) 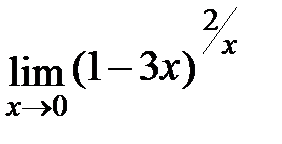 .
. 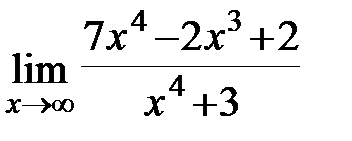 ;б)
;б) 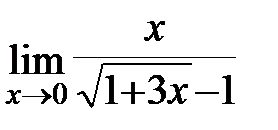 ; в)
; в) 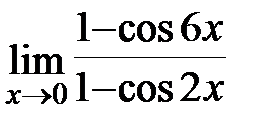 ; г)
; г) 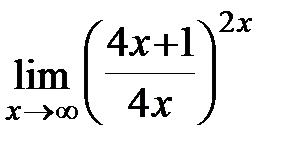 .
. 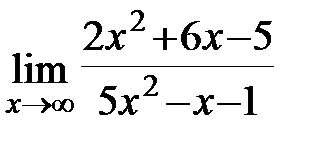 ;б)
;б) 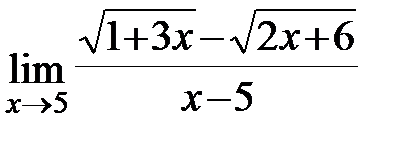 ; в)
; в) 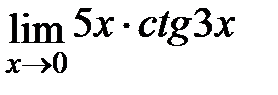 ; г)
; г) 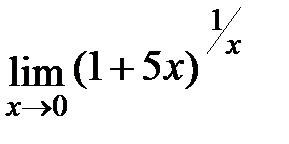 .
. 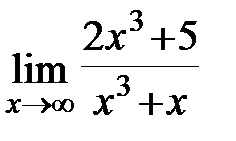 ;б)
;б) 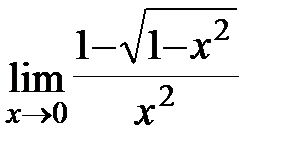 ; в)
; в) 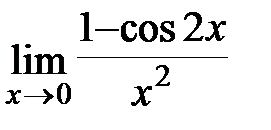 ; г)
; г) 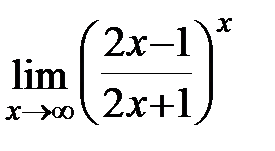 .
. 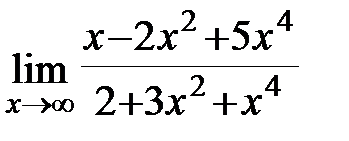 ;б)
;б) 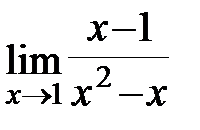 ; в)
; в) 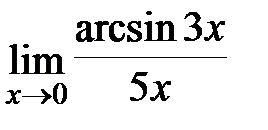 ; г)
; г) 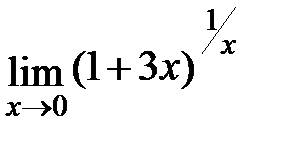 .
. 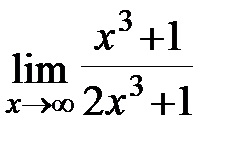 ;б)
;б) 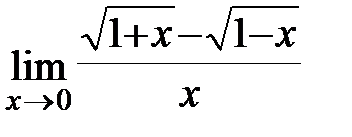 ; в)
; в) 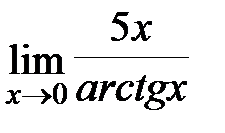 ; г)
; г) 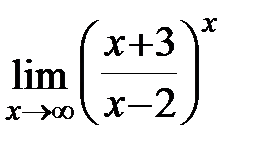 . Задание 4.Отыскать производные
. Задание 4.Отыскать производные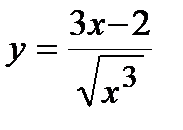 , б)
, б) 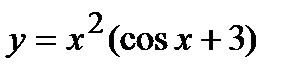 , в)
, в) 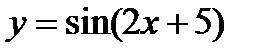 . 2. а)
. 2. а) 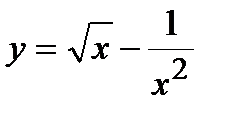 , б)
, б) 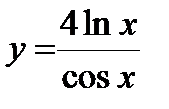 , в)
, в) 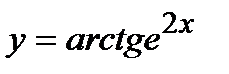 . 3. а)
. 3. а) 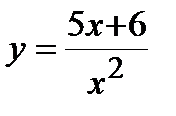 , б)
, б) 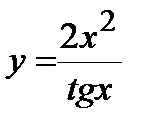 , в)
, в) 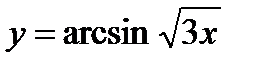 . 4. а)
. 4. а) 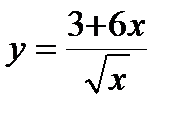 , б)
, б) 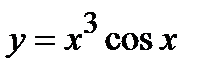 , в)
, в) 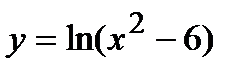 . 5. а)
. 5. а) 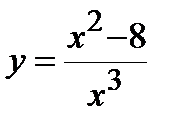 , б)
, б) 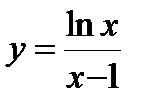 , в)
, в) 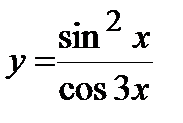 . 6. а)
. 6. а) 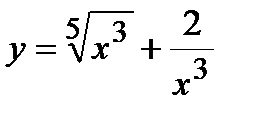 , б)
, б) 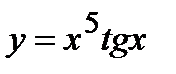 , в)
, в) 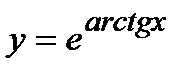 . 7. а)
. 7. а) 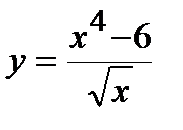 , б)
, б) 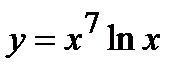 , в)
, в) 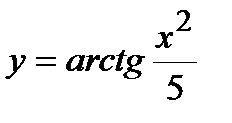 . 8. а)
. 8. а) 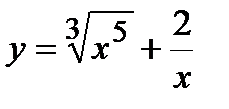 , б)
, б) 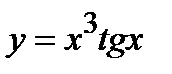 , в)
, в) 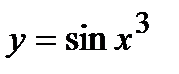 . 9. а)
. 9. а) 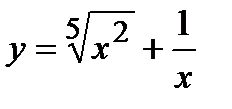 , б)
, б) 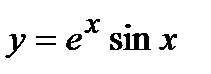 , в)
, в) 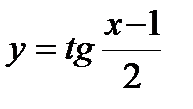 . 10. а)
. 10. а) 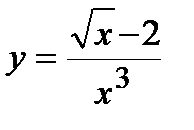 , б)
, б) 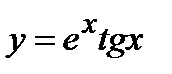 , в)
, в) 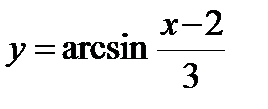 .
. 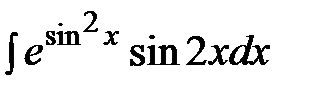 ; б)
; б) 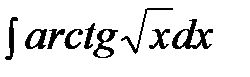 ; в)
; в) 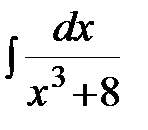 ; г)
; г) 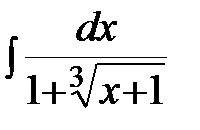 .
. 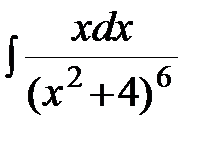 ; б)
; б) 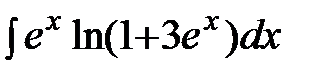 ; в)
; в) 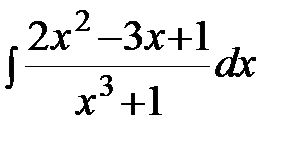 ; г)
; г) 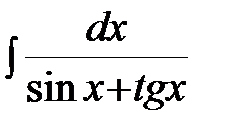 .
. 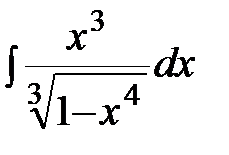 ; б)
; б) 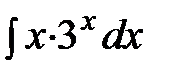 ;
; 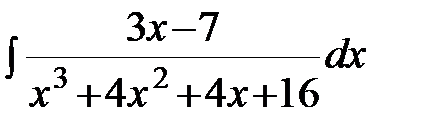 ; г)
; г) 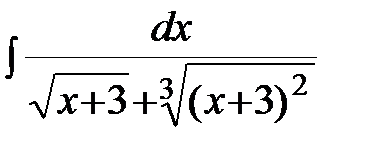 .
. 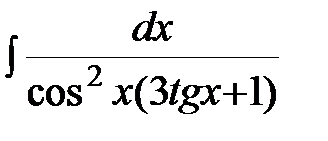 ; б)
; б) 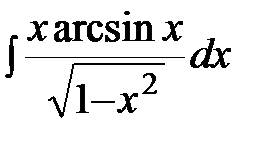 ; в)
; в) 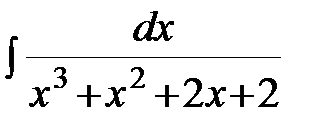 ; г)
; г) 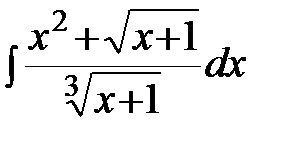 .
. 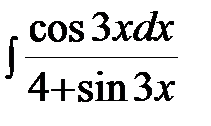 ; б)
; б) 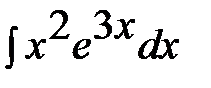 ;
; 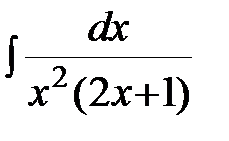 ; г)
; г) 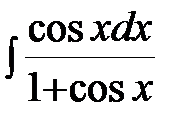 .
. 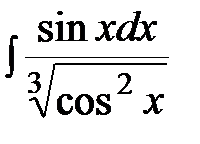 ; б)
; б) 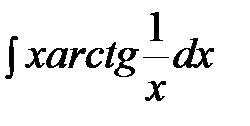 ; в)
; в) 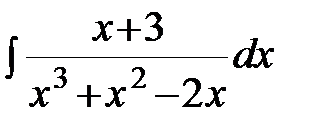 ; г)
; г) 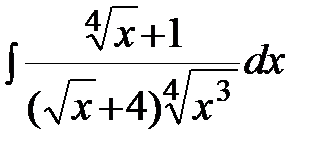 .
. 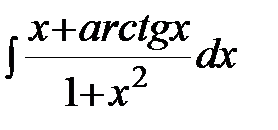 ; б)
; б) 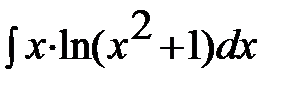 ; в)
; в) 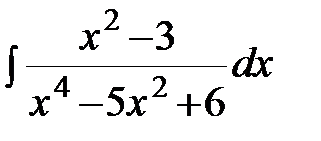 ; г)
; г) 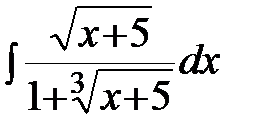 .
. 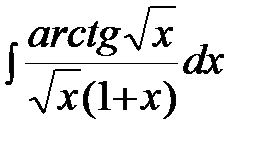 ; б)
; б) 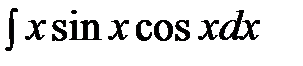 ; в)
; в) 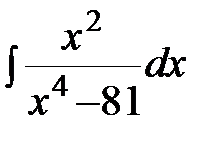 ; г)
; г) 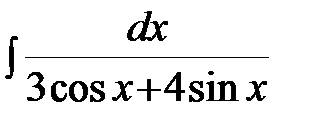 .
. 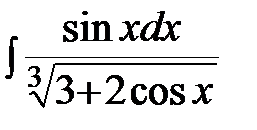 ; б)
; б) 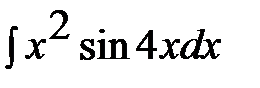 ; в)
; в) 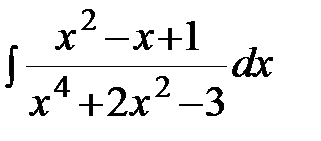 ; г)
; г) 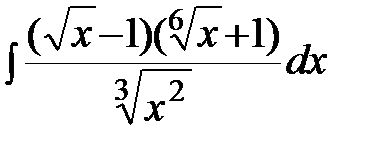 .
. 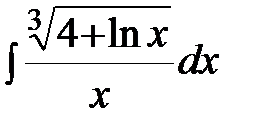 ; б)
; б) 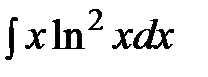 ; в)
; в) 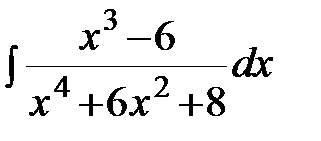 ; г)
; г) 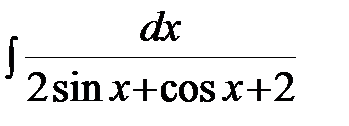 .
.