Подведение под знак дифференциала.

Задача 12. Вычислить .

Ответ. Подмечаем, что присутствует множитель , что есть производной от . А другая часть функции именно зависит лишь от . Исходя из этого возможно подвести под символ дифференциала: =

Используем замену : = .

Потом, = 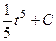, и по окончании обратной замены .

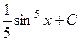Ответ. .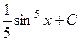

Задача 13.Вычислить интеграл .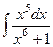

Ответ. = = = = =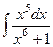

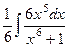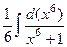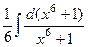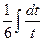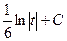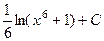= = . Учитывая тот факт, что , символ модуля не нужен.

Ответ. .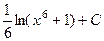

Задача 14. Вычислить .

Ответ. = = = = = .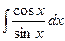

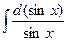Ответ. .

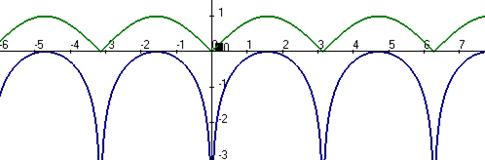
Для сведения, продемонстрируем, как выглядит график функции .

Зелёным цветом изображён график , синим .

Вертикальные асимптоты .

Задача 15. Вычислить интеграл .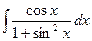

Ответ. = = = =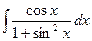

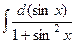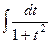. Ответ. .

Домашнее задание.

1.Вычислить интеграл . Ответ. .

2. Вычислить интеграл 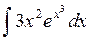. Ответ. .

3.Вычислить интеграл 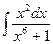. Ответ. .

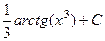4. Вычислить интеграл . Ответ. .

ПРАКТИКА № 2

Задача 1. Вычислить .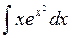

Ответ. = = = = = .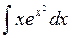

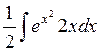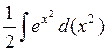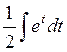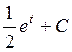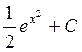Ответ. .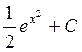

Задача 2. Вычислить .

Ответ. = = =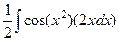

= = = .

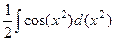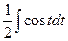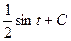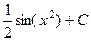Ответ. .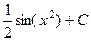

Задача 3. Вычислить .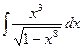

Ответ. = = = = = .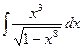

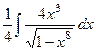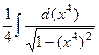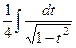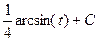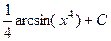Ответ. .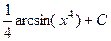

Задача 4. Вычислить .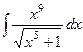

Ответ.В случае, если сходу подвести под символ дифференциала то, что имеется в числителе, то будет , но тогда в знаменателе окажется выражение . дабы не происходило для того чтобы усложнения и не показались положенные квадратные корни, нужно подводить отнюдь не весь числитель, а отделить тот множитель, что нам эргономичнее, дабы позже всё выражалось через .

= = =

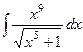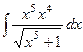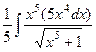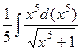
и сейчас, по окончании замены , окажется .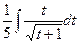

Потом, сделаем преобразование, котрое разрешит покинуть лишь однотипные корни:

= = =

=

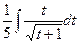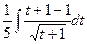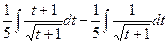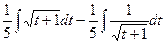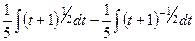
потом уже посредством простых действий со степенными функциями:

= .

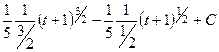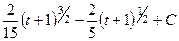По окончании обратной замены приобретаем ответ, наряду с этим кроме этого заодно обратно меняем дробные степени на корни.

Ответ. .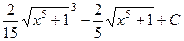

Задача 5. Вычислить .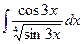

Ответ. = =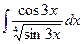

= = = =

= = .

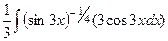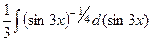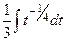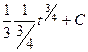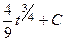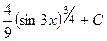Ответ. .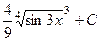

Задача 6. Вычислить .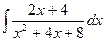

Ответ. Увидим, что в числителе производная того выражения, которое имеется в знаменателе. Тогда = = = = .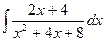

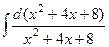Тут практически мы применили замену для упрощения выражения. Кстати, выделение полного квадрата в знаменателе это тут был бы тупиковый путь, поскольку в числителе не константа а многочлен, другими словами не удалось бы свести к виду .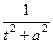

Ответ. .

Задача 7. Вычислить .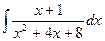

Ответ. Тут, в отличие от прошедшей задачи, в числителе уже произвольный многочлен, не соответствующий производной от знаменателя. Однако, возможно путём арифметических операций взять в том месте дифференциал знаменателя:

Домножим и поделим на 2, дабы исправился коэффициент при :

=

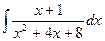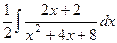
Сейчас осталось прибавить и забрать 2, и будет получено :

= =

= .

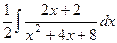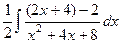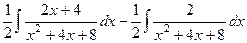В первом слагаемом делается ровно то же самое, что в прошедшей задаче, а во втором — выделить полный квадрат, и в итоге сводится к арктангенсу:

=

.

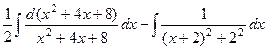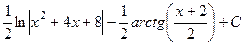Ответ. .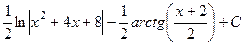

Задача 8. Вычислить .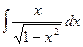

Ответ. Не обращая внимания на то, что интеграл похож на 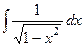, но, однако, в числителе имеется переменная , исходя из этого это не табличный интеграл, и ответ тут вовсе не арксинус. Увидим, что в числителе 1-я степень, а под корнем в знаменателе 2-я. Домножим и поделим так, дабы в числителе выяснилось то выражение, которое под корнем в знаменателе.

= =

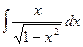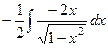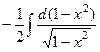
по окончании замены переменной, это возможно переписать так: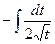

соответственно, и по окончании обратной замены:

Ответ. .

Задача 9. Вычислить .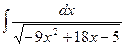

Ответ. = = = = .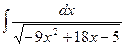

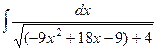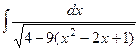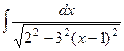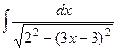Чтобы применить формулу,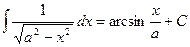

необходимо обозначить . Но сперва сделаем так, дабы и в числителе был не просто а :

= = .

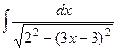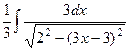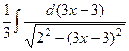Сейчас интеграл имеет форму 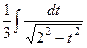, и равен .

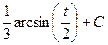По окончании обратной замены приобретаем ответ.

Ответ. .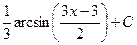

Задачи по теме «Интегрирование по частям»

Отыскать в памяти формулу .

Задача 10. Вычислить .

Ответ. Пускай , так нужно, дабы понизилась степень на следующем шаге. Составим таблицу:

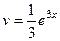
Тогда = = .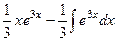

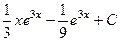Ответ. .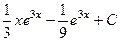

Домашние задачи.

1. 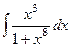Ответ. 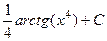. Указание. См. задачу № 3.

2. 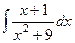Ответ. .

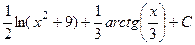Указание. См. задачу № 7.

3. 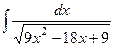. Ответ. 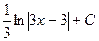. Указание. См. задачу № 9.

ПРАКТИКА № 3

Задача 1. Вычислить интеграл .

Ответ.

= = .

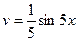
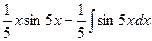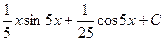Задача 2. Вычислить интеграл .

Ответ. Так как степени и 2-степенная функция, то эта задача решается в 2 шага. На первом шаге, обозначаем , .

Тогда = .

На 2-м шаге, обозначим , .

В скобке происходит вычисление как бы для нового примера, выполним это положенное воздействие:

= = .

Итак, ответ: .

Задача 3. Вычислить интеграл

Ответ. Пускай , второго множителя нет, но мы формально можем вычислять, что он имеется, лишь равен 1. Итак, .

Выстроим таблицу:

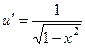
Тогда = =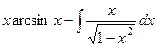

= =

= .

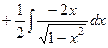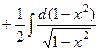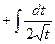Ответ: .

Задача 4.Вычислить интеграл

Производная арктангенса это рациональная дробь. И это мы используем, обозначая её при интегрировании по частям:

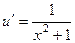
Тогда: = .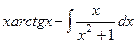

Второе слагаемое потом уже решается подведением под символ dx.

= =

= =

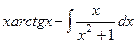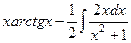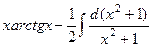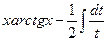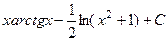. Символ модуля кроме того не нужен, т.к. .

Задача 5. Вычислить интеграл .

Ответ.На этом примере вы заметите, что время от времени полезно отойти от того, что мы, в большинстве случаев, степенную функцию обозначали через u.

Дело в том, что в случае, если так сделать, то при переходе от dv к v появляется целая новая задача, которая связана с поиском интеграла от арктангенса. Наоборот, в случае, если , то его производная состоит лишь из степенных, другими словами происходит большое упрощение. Конечно же тут нужно будет смириться с тем что усложняется, растёт его степень, т.е. перейдёт в 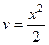, но арктангенс упрощается сильно. Итак, выстроим таблицу:

= = =

= =

= .

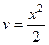
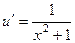
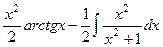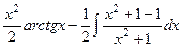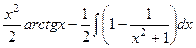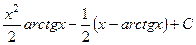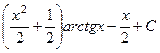Задача 6. Вычислить интеграл

Ответ.Пускай .

. На первом шаге, обозначаем , .

. = .

На 2-м шаге, в том интеграле, что оказался, обозначим подобным образом: , .

Получается = = .

Из равенства возможно выразить :

, .

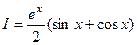Примечание. Интегралы вида и именуются «циклические интегралы», в силу того, что они решаются таким методом: через 2 цикла вычисления получается сведение к исходному интегралу.

Ответ. = .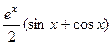

Задача 7. Вычислить .

Ответ.На первом шаге,

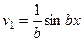
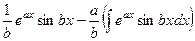= . Сейчас в скобках подобное выражение, применим к нему такие же преобразования.

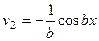
Продолжим преобразования:

=

.

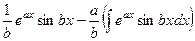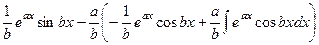По окончании двух действий, мы видим опять интеграл в конце строчка.

Возможно записать так, раскрыв скобки:

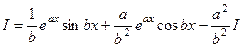. А сейчас возможно это арифметическим путём.

.

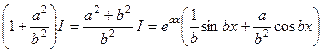
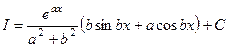Итак, = .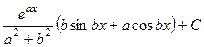

Задача 8. Взять формулу вычисления интегралов вида .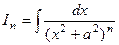

Ответ.Обозначим всю функцию через u и применим интегрирование по частям, и наряду с этим формально вычисляем второй множитель равным 1. Для удобства, временно применим отрицательные степени вместо дробей.

= = =

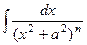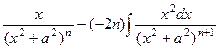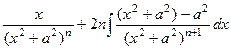
Сейчас можем разбить на две дроби, интеграл от первой сводится к , а второй к .

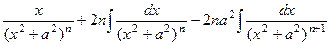= , другими словами

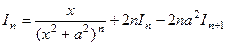, откуда выразим через :

,

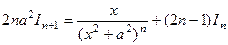вывели «рекурсивную» формулу 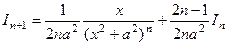, благодаря которой интеграл для того чтобы типа для большей степени сводится к меньшей степени, соответственно, все они последовательно сводятся к 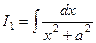, что равен .

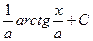Задача 9. Вычислить интеграл .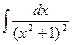

Ответ. Применим формулу, наряду с этим n+1 = 2 (n=2 было бы неправильно, поскольку в формуле та степень, которую высказываем, это n+1 а та, через которую, это n).

Наряду с этим n = 1. a = 1.

Формула получает таковой вид: .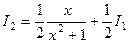

Ответ: = .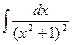

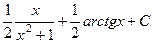Домашнее задание.

1. Вычислить . (как в задаче 6).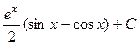

2. Вычислить . (как в 7).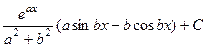

3.Вычислить 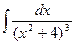либо 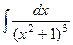(по рекурсивной формуле).

Поднесение под знак дифференциала

Интересные записи:

• Понедельник, 10 мая 2010 года
• По модулю 1. история зарубежной литературы
• Пользование устройствами алсн и контроля бдительности машиниста в пути следования
• Понятие бюджетного права, его источники