Рис. 15.1
3 ВОПРОС
В точке А (рис. 15.1, б) поперечного сечения оси вагона имеем:
ГЛАВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
При изучении прочности, устойчивости и жёсткости элементов конструкций в сопротивлении материалов применяют последовательность предпосылок (допущений), упрощающих расчеты. Эти предпосылки, как показывают опыты, и изучения, совершённые более строгими способами теории упругости, возможно применять при ответе большинства задач, разглядываемых в сопротивлении материалов. В некоторых случаях, намерено оговариваемых, часть допущений применять запрещено, поскольку это дало бы неправильные результаты.
Главные предпосылки в сопротивлении материалов следующие.
1. Материал конструкции есть однородным и целым, т. е. его свойства не зависят от размеров и формы тела и однообразны во всех его точках.
Это положение разрешает не учитывать дискретную, атомистическую структуру вещества и тем более перемещение отдельных молекул, составляющих тело. Оно используется кроме того при расчете конструкций из для того чтобы неоднородного материала, как бетон, складывающегося из щебня, связанного цементным раствором. Это возможно делать по причине того, что размеры отдельных частиц материала малы если сравнивать с размерами сечений элементов конструкции.
Эта предпосылка разрешает, разглядывая при теоретическом анализе бесконечно малый элемент конструкции, наделять его особенностями, которыми владеет количество тела настоящих размеров.
2. Материал конструкции изотропен, т. е. свойства его по всем направлениям однообразны.
Эта предпосылка употребляется при ответе большинства задач сопротивления материалов, не смотря на то, что для некоторых материалов она очень условна (к примеру, для дерева, свойства которого в направлениях на протяжении и поперек волокон разны). Такие материалы, свойства которых в разных направлениях разны, именуются анизотропными. При ответе некоторых задач нужно учитывать разные особенности материала в разных направлениях, т. е. его анизотропию.
3. Материал конструкции владеет свойством совершенной упругости, т. е. свойством абсолютно восстанавливать начальные размеры и форму тела по окончании устранения обстоятельств, позвавших его деформацию. Деформация идеально упругого тела в любой момент времени зависит лишь от нагрузок, действующих сейчас на тело, и не зависит от того, в какой последовательности нагрузки приложены.
Эта предпосылка честна только при напряжениях, не превышающих для данного материала определенной, постоянной величины, именуемой пределом упругости. При напряжениях, превышающих предел упругости, в материале появляются либо пластические (остаточные) деформации, не исчезающие по окончании снятия нагрузка, либо упруго-пластические — частично исчезающие.
Предпосылка об совершенной упругости материала употребляется при ответе большинства задач сопротивления материалов.
4. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в данной точке.
Эта предпосылка, в первый раз сформулированная Р. Гуком, именуется законом Гука.
Закон Гука честен для большинства материалов, но для каждого из них только при напряжениях, не превышающих некоей величины (предела пропорциональности). Данный закон употребляется при ответе большинства задач сопротивления материалов.
5. Деформации конструкции предполагаются так малыми, что возможно не учитывать их влияния на обоюдное размещение нагрузок и на расстояния от нагрузок до любых точек конструкции.
Вопрос о возможности применения данной предпосылки решается в каждом отдельном случае с учетом не только вида конструкции, вместе с тем величины и характера действующей на нее нагрузки. Так, к примеру, при расчете балки, изображенной на рис. 11.1, а, возможно не учитывать ее деформации (при определении упрочнений в ней), в случае, если прогиб (дельта) намного меньше высоты h поперечного сечения. При расчете же балки, продемонстрированной на рис. 11.1, б, ее деформацию возможно не учитывать кроме того тогда, в то время, когда прогиб больше высоты Н, при условии, что он мал если сравнивать с длиной бруса I.
6. Итог действия на конструкцию совокупности нагрузок равен сумме результатов действия каждой нагрузки в отдельности.
Это положение носит название принципа независимости действия сил. Его довольно часто именуют кроме этого принципом наложения. Он применим в тех случаях, в то время, когда смогут быть использованы закон Гука (см. выше — п. 4) и предпосылка о малости деформаций (см. п. 5), так как есть их следствием.
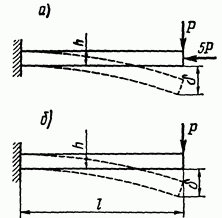
Рис. 11.1
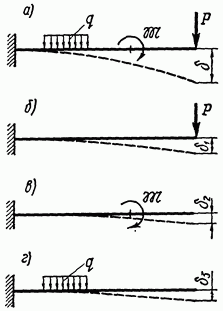
Рис. 12.1
Из принципа наложения направляться, что напряжения точек и перемещения конструкции в ней прямо пропорциональны величине нагрузки.
Разглядим брус, изображенный на рис. 12.1 , а, нагруженный силой Р, моментом и равномерно распределенной нагрузкой q. Из принципа независимости действия сил направляться, что, к примеру, прогиб б финиша бруса от нагрузок , равен сумме прогибов (рис. 12.1, б, в, г) от действия каждой нагрузки в отдельности, т. е.
Подобно возможно отыскать прогибы любых вторых точек бруса, внутренние упрочнения в его поперечных сечениях и напряжения.
Принцип независимости действия сил не распространяется на работу внешних и внутренних сил и на потенциальную энергию (см. § 6.2).
7. Поперечные сечения бруса, плоские до приложения к нему нагрузки, остаются плоскими и при действии нагрузки.
Эта предпосылка именуется догадкой плоских сечений, либо догадкой Бернулли. Она играется только ключевую роль в сопротивлении материалов и употребляется при выводе большинства формул для расчета брусьев