Дифференциальное уравнение первого порядка
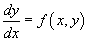именуется однородным, в случае, если правая часть удовлетворяет соотношению
для всех значений t. Иначе говоря правая часть обязана являться однородной функцией нулевого порядка по отношению к переменным x и y:
Однородное дифференциальное уравнение возможно кроме этого записать в виде
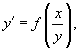либо через дифференциалы:
где P(x,y) и Q(x,y) ? однородные функции однообразного порядка.
Определение однородной функции
Функция P(x,y) именуется однородной функцией порядка n, в случае, если для всех t 0 справедливо следующее соотношение:
Ответ однородных дифференциальных уравнений
Однородное дифференциальное уравнение возможно решить посредством подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
Дифференциальное уравнение вида
преобразуется в уравнение с разделяющимися переменными при помощи переноса начала совокупности координат в точку пересечения прямых линий, заданных в уравнении. В случае, если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными методом замены переменной:
Пример 1
Решить дифференциальное уравнение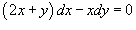 
.
Ответ. Нетрудно подметить, что многочлены P(x,y) и Q(x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Исходя из этого, данное дифференциальное уравнение кроме этого будет однородным.
Положим y = ux, где u ? некая новая функция, зависящая от x. Тогда
Подставляя это в дифференциальное уравнение, приобретаем
Следовательно,
Поделим обе части уравнения на x:
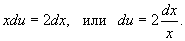Делая деление x, мы имели возможность утратить ответ x = 0. Прямая подстановка говорит о том, что x = 0 вправду есть одним из ответов отечественного уравнения.
Интегрируем последнее выражение:
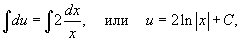где C ? постоянная интегрирования.
Возвращаясь к ветхой переменной y, возможно записать:
Так, уравнение имеет два решения:
Пример 2
Решить дифференциальное уравнение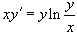 
.
Ответ. Увидим, что корень x = 0 не в собственности области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме:
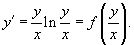Как видно, уравнение есть однородным.
Сделаем замену y = ux. Следовательно,
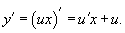
Подставляем полученное выражение в дифференциальное уравнение:
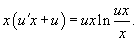
Поделим обе части на x ? 0:
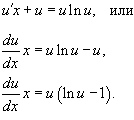
В следствии мы приобретаем уравнение с разделяющимися переменными:
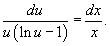
На следующем шаге проинтегрируем левую и правую части уравнения:
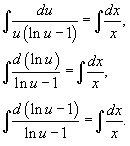
Следовательно,
Постоянную C тут возможно записать как ln C1 (C1 0). Тогда
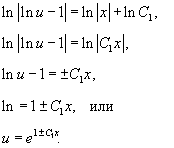
Так, мы взяли два решения:
В случае, если C1 = 0, то ответом есть функция y = xe. Легко убедиться, что эта функция будет кроме этого и ответом дифференциального уравнения. В действительности, подставляя
в дифференциальное уравнение, находим:
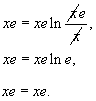
Так, все решения дифференциального уравнения возможно представить одной формулой:
где C ? произвольное настоящее число.
Решить дифференциальное уравнение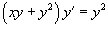 
.
Ответ. Тут мы опять видимся с однородным уравнением. В действительности, запишем его в виде:
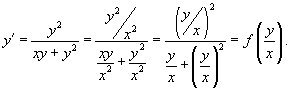
Сделаем подстановку y = ux. Тогда y’ = u’x + u. Подставляя y и y’ в исходное уравнение, приобретаем:
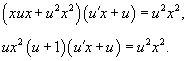
Поделим обе части уравнения на ux2. Увидим, что корень x =0 не есть ответом, но возможно убедиться, что корень u = 0 (либо y = 0) будет одним из ответов данного дифференциального уравнения.
В следствии приобретаем:
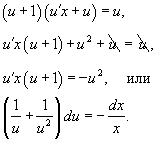
Интегрируя, находим неспециализированное ответ:
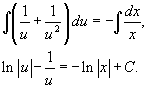
Учитывая, что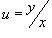 
, последнее выражение возможно записать в форме
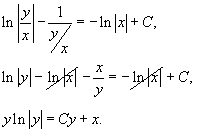
Обратная функция x(y) имеет явный вид:
Потому, что C ? произвольное число, символ минус перед данной константой возможно заменить на символ плюс. Тогда приобретаем:
Так, дифференциальное уравнение имеет решения:
Пример 4
Решить дифференциальное уравнение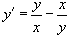 
.
Ответ. Из вида правой части уравнения направляться, что x ? 0 и y ? 0. Возможно сделать подстановку: y = ux, y’ = u’x + u, которая ведет к уравнению с разделяющимися переменными:
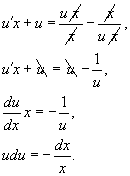
Интегрируя данное уравнение, приобретаем:
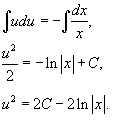
Переобозначим 2C легко как постоянную C. Следовательно,
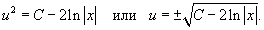
Итак, неспециализированное ответ записывается в виде:
Пример 5
Отыскать неспециализированное ответ дифференциального уравнения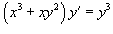 
.
Ответ. Как видно, данное уравнение есть однородным. Исходя из этого, воспользуемся подстановкой y = ux, y’ = u’x + u. В следствии уравнение преобразуется в уравнение с разделяющимися переменными:
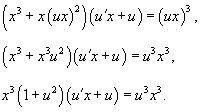
Поделим обе части на x3. (Увидим, что корень x = 0 не есть ответом).
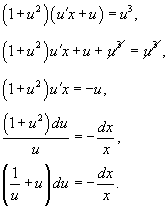
Сейчас возможно проинтегрировать последнее уравнение:
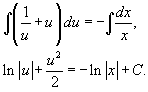
Так как u = y/x, то ответ записывается в виде:
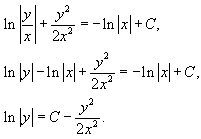
Из этого следует, что
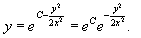
Переобозначим для краткости: eC = C1, (C1 0). Тогда ответ в неявной форме определяется уравнением:
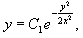
Пример 6
Решить уравнение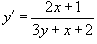 
.
Ответ. Видно, что знаменатель и числитель в правой части соответствуют пересекающимся прямым. Исходя из этого данное дифференциальное уравнение возможно преобразовать в однородное методом соответствующего преобразования координат. Пускай старые координаты и новые связаны соотношениями:
Константы ? и ? мы определим позднее. Подставляя указанные соотношения в уравнение, приобретаем:
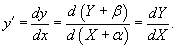
В новых координатах дифференциальное уравнение принимает вид:
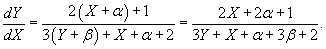
Данное уравнение будет однородным, в случае, если коэффициенты ? и ? будут удовлетворять совокупности уравнений
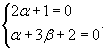
Решая данную совокупность уравнений довольно ? и ?, находим:
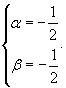
При указанных значениях ? и ? дифференциальное уравнение записывается следующим образом:
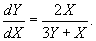
Мы взяли однородное уравнение. Потом делаем замену: Y = uX, где u ? некая функция X. Следовательн, dY = Xdu + udX. В итоге мы имеем:
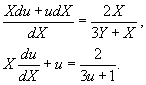
Поделим знаменатель и числитель в правой части на X. Возможно проверить, что X = 0 либо x = X + ? = ?1/2 не есть ответом дифференциального уравнения.
Простые преобразования приводят к следующему результату:
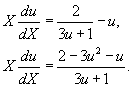
Разложим квадратичную функцию в числителе дроби в правой части на произведение одночленов:
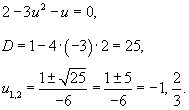
Следовательно,
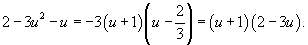
Тогда
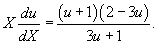
Разделяя переменные, возможно записать:
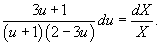
Интегрируем полученное уравнение:
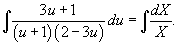
Сейчас преобразуем подынтегральное выражение в левой части. Воспользуемся способом неизвестных коэффициентов и разложим подынтегральное выражение на сумму рациональных дробей:
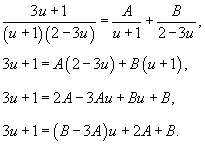Следовательно,
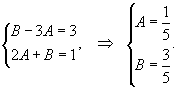
Так, дифференциальное уравнение записывается в следующем виде:
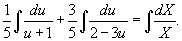
По окончании интегрирования обеих частей приобретаем:
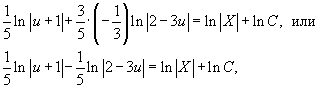
где постоянная C есть хорошим настоящим числом.
Перепишем ответ через переменные X и Y:
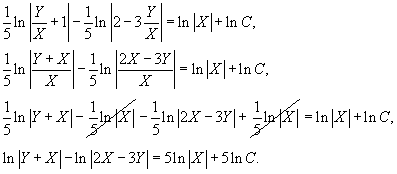
Потом комфортно обозначить: 5lnC = lnC1, где C1 ? произвольное положительное число. Так, ответ возможно записать в виде:
Сейчас мы можем возвратиться к начальным переменным x,y. Так как
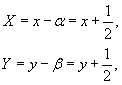то приобретаем:
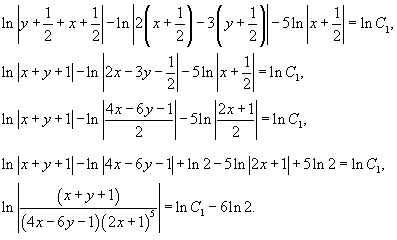
Правую часть возможно опять пара упростить:
Тогда окончательное неспециализированное ответ исходного дифференциального уравнения выражается следующей неявной формулой:
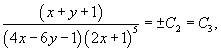где постоянная C3 ? любое число, не равное нулю.
Пример 7
Отыскать неспециализированное ответ дифференциального уравнения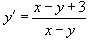 
.
Ответ. Возможно подметить, что уравнения прямых в знаменатель и числитель в правой части соответствуют параллельным прямым. Исходя из этого, сделаем следующую замену переменных:
В следствии дифференциальное уравнение принимает вид:
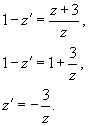
Как видно, мы взяли простое уравнение с разделяющимися переменными. Решая его, находим ответ:
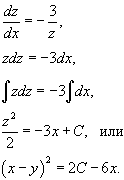
Из последнего выражения возможно вывести явную функцию y(x):
Так,
4. Линейные уравнения. Определение, способы ответов, примеры
Линейные уравнения.ДУ первого порядка именуется линейным, в случае, если малоизвестная функция y(x) и её производная входят в уравнение в первой степени
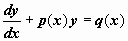(14)
Тут p(x), q(x) — постоянные функции.
Для решения уравнения (14) представим y(x) в виде произведения двух новых малоизвестных функций u(x) и v(x): y(x) = u(x) v(x). Тогда , и уравнение приводится к виду , либо . Это уравнение решаем в два этапа: сперва находим функцию v(x) как частное ответ уравнения с разделяющимися переменными ; после этого находим u(x) из уравнения . Итак,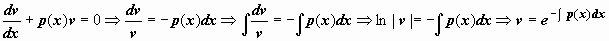 
(мы не вводим в это решение произвольную постоянную C, нам достаточно отыскать одну функцию v(x), обнуляющую слагаемое со скобками в уравнении ). Сейчас уравнение для u(x) запишется как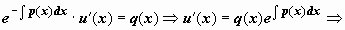 
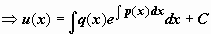. Неспециализированное ответ уравнения 
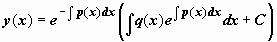. Запоминать эту формулу не нужно, лучше усвоить порядок действий и воспроизводить его при ответе каждой задачи.
Пример: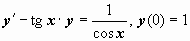 
.
Ответ: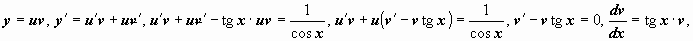 
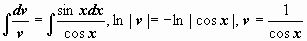. Сейчас для u(x) возьмём: 
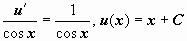, и неспециализированное ответ уравнения 
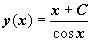. Для нахождения частного ответа, соответствующего начальным условиям задачи Коши, подставим в неспециализированное ответ 
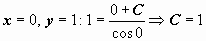. Ответ задачи: 
.
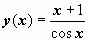Данный способ ответа линейных уравнений довольно часто реализуется по-второму — в форме вариации произвольной постоянной. Уравнение (14) именуется однородным, в случае, если q(x) = 0. Пускай дано неоднородное уравнение (14) . Оно, как и в прошлом случае, решается в два этапа. Обнулим правую часть, оказавшееся уравнение будем именовать однородным уравнением, соответствующим уравнению (14): . Решаем это уравнение: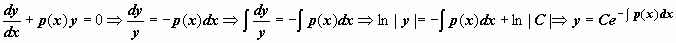 
(при делении на y теряется ответ y (x) = 0, но оно входит в неспециализированное ответ при C = 0). Сейчас ищем неспециализированное ответ уравнения (14) в виде 
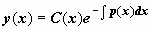, где — новая малоизвестная функция; находим производную 
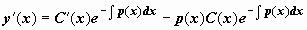и подставляем в (14) y и : 
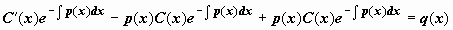, либо 
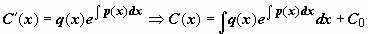, где . Сейчас 
.
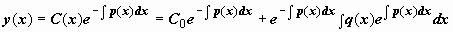Ясно, что обе реализации ответа имеют один суть (ответ однородного уравнения играет роль функции v(x), варьируемая постоянная C(x) — роль функции u(x)).
Отметим ещё одно ответственное событие. Переменные x и y, входящие в уравнение, равноправны, исходя из этого при определении типа уравнения нужно иметь в виду, что может оказаться предпочтительней искать ответ в виде x = x(y), а не в виде y = y(x).
Пример: (x + y2)dy = ydx. В случае, если мы представим это уравнение в виде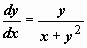 
, то решить его не сможем, поскольку оно не в собственности ни одному из рассмотренных типов. В случае, если же представить его в виде 
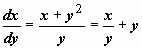, то относительно функции x = x(y) оно линейно. Решаем его способом вариации произвольной постоянной. Соответствующее однородное уравнение: 
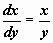. Его ответ: 
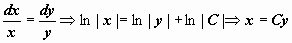. Ищем ответ данного уравнения в форме x = C(y) y. Тогда 
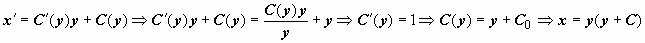(постоянная C0 переобозначена как ). Утерянное ответ — y = 0.
5. Уравнение Бернулли. Определение, способы ответов, примеры
Уравнение Бернулли. Так именуется уравнение
(15)
где (при m = 0 уравнение линейно, при m = 1 — с разделяющимися переменными). Это уравнение решается одним из следующих способов:
1. Уравнение Бернулли сводится к линейному подстановкой z = y1-m (при m1 возможно утрачено ответ y = 0). Вправду, ,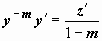 
; по окончании деления уравнения (15) на ym возьмём , либо 
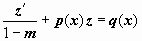— линейное уравнение.
Пример: (уравнение Бернулли, m = 2). Подстановка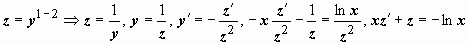 
. Решаем полученное линейное уравнение: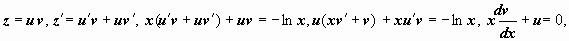 
.
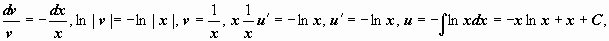
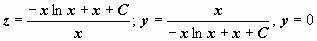2. Возможно сходу решать уравнение Бернулли способом, которым решаются линейные уравнения, т.е. заменой y(x) = u(x) v(x):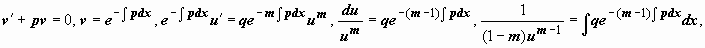 
из этого выражения находим u(x), и y(x) = u(x) v(x).
Пример: решить задачу Коши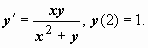 
Как и в прошлом примере, это уравнение не попадает ни под один из рассмотренных типов: оно не есть ни уравнением с разделяющимися переменными (наличие суммы x2 + y), ни уравнением с однородной правой частью (слагаемые различных порядков — первого и второго в данной сумме), ни линейным, ни Бернулли (вторая структура). Попытаемся снова представим это уравнение как уравнение довольно x = x(y): 
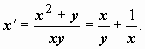Это уже уравнение Бернулли с m = -1. Начальное условие примет вид x(1) = 2. Решаем уравнение: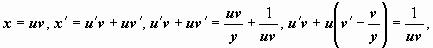 
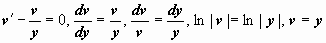. Тогда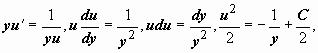 
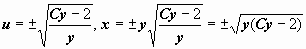. Это неспециализированное ответ уравнения (утерянное ответ y = 0 не удовлетворяет начальному условию). Ищем частное ответ, удовлетворяющее начальному условию: 
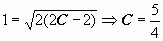; ответ задачи Коши: 
.
6. Уравнения в полных дифференциалах, способ ответа, примеры
Уравнение в полных дифференциалах. Так именуется уравнение вида
P(x, y) dx + Q(x, y) dy = 0. (16)
(P(x, y), Q(x, y) — непрерывно дифференцируемы) , если его левая часть есть полным дифференциалом некоей функции u(x, y), т.е. в случае, если существует такая функция u(x, y), что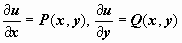 
. Нужным и достаточным условием существования таковой функции есть условие 
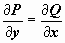. В случае, если (16) — уравнение в полных дифференциалах, то его правая часть равна 
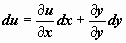, т.е. (16) принимает вид du(x, y) = 0. На ответе y(x) возьмём du(x, y(x)) = 0, следовательно, u(x, y(x)) = C, где C — произвольная постоянная. Соотношение u(x, y) = C и имеется неспециализированное ответ уравнения в полных дифференциалах.
Для нахождения функции u(x, y) решается совокупность уравнений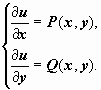 
Из первого уравнения данной совокупности находим с точностью до произвольной дифференцируемой по y функции (эта функция играет роль постоянной интегрирования; так как интегрирование ведётся по переменной x); после этого из второго уравнения определяется .
Пример: отыскать неспециализированное ответ уравнения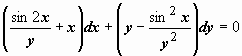 
. Убедимся, что это — уравнение в полных дифференциалах. Тут 
; 
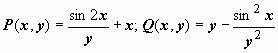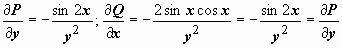, т.е. это вправду уравнение разглядываемого типа. Ищем функцию u(x, y) такую, что 
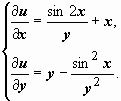Из первого уравнения 
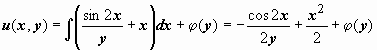. Дифференцируем эту функцию по y и приравниваем выражению, стоящему во втором уравнении совокупности: 
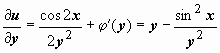. В случае, если мы верно решаем это уравнение (т.е. верно выяснили его тип и верно выполнили прошлые действия), то в взятом уравнении для должны остаться лишь члены, зависящие от y. Вправду, воображая как , возьмём 
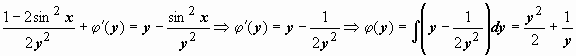. Следовательно, 
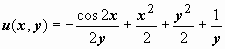, и неспециализированное ответ уравнения имеет форму 
.
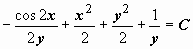14.3.6. особые решения и Особые точки уравнения первого порядка. В случае, если в окрестности точки (x0, y0) плоскости для уравнения выполняются единственности решения и условия существования задачи Коши (непрерывность f(x, y) и ), то через эту точку проходит единственная интегральная кривая. В случае, если эти условия нарушаются, точку (x0, y0) именуют особенной точкой дифференциального уравнения. Через особенную точку может не проходить ни одной интегральной кривой (т.е. задача , y(x0) = y0 не имеет решения); может проходить одна интегральная кривая; может проходить пара интегральных кривых. Особенные точки смогут образовать кривую, которая сама есть интегральной кривой уравнения. Ответ уравнения, в каждой точке которого нарушается его единственность, именуют особенным ответом. Для примера разглядим уравнение . Тут — постоянна в любой точке (x, y), но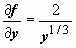 
— не имеет конечного предела при , т.е. в любой точке (x, y) при y = 0 нарушается условие существования постоянной производной . Следовательно, каждая точка (x, 0) есть особенной точкой уравнения. Прямая y = 0, разумеется, интегральная кривая уравнения (функция y = 0 удовлетворяет уравнению). Отыщем неспециализированное ответ этого уравнения: 
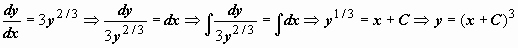. Пара таких функций приведено на рисунке справа вверху вместе с ответом y = 0. В любой точке (x, 0) нарушается единственность ответа, так, ответ y = 0 — особенное. В действительности через любую точку (x, 0)проходит нескончаемое количество интегральных кривых, поскольку каждая кривая, составленная из частей особенного и неособых ответов (одна такая кривая выделена красным пунктиром), кроме этого есть интегральной кривой.