Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 4.
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 15.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 5.
Главные определения
Отметим, что осевыми моментами инерции плоской фигуры довольно произвольных осей и именуются величины
; 
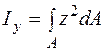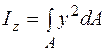. (5.13)
Центробежным моментом инерции есть величина
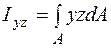. (5.14)
Оси именуются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты довольно этих осей равны нулю. Главными осями инерции фигуры именуются оси, довольно которых центробежный момент инерции равен нулю. В случае, если фигура имеет хотя бы одну ось симметрии, то эта ось есть основной осью.
Для вычисления моментов инерции относительно главных центральных осей нужно мочь обнаружить положение центра тяжести фигуры и знать, как изменяются моменты инерции при повороте осей и параллельном переносе. Напомним уже узнаваемые студенту формулы и приведем новые.
Определение центра тяжести фигуры производится по формулам
; 
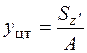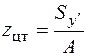, (5.15)
где запасные оси , , довольно которых вычисляются статические моменты, выбираются произвольно.
При параллельном переносе осей моменты инерции изменяются по следующим законам:
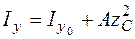; (5.16)
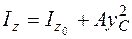; (5.17)
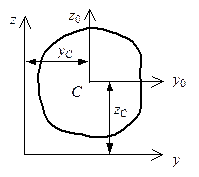 Рис. 5.13. Параллельный перенос осей |
. (5.18)
В формулах (5.16)–(5.18) , , – моменты инерции довольно центральных осей; , – координаты центра тяжести (точки на рис. 5.13) в совокупности осей , , параллельных центральным осям , (см. рис. 5.13). Увидим, что в случае, если при вычислении осевых моментов инерции символы координат не имеют значения, то при определении центробежного момента инерции символы координат , нужно непременно учитывать.
При повороте осей (рис. 5.14) координаты точки изменяются по известному закону
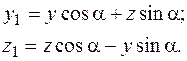(5.19)
Подставляя эти формулы в (5.13)–(5.14), возьмём, что моменты инерции изменяются следующим образом:
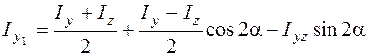; (5.20)
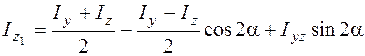; (5.21)
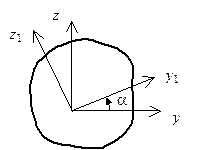 Рис. 5.14. Поворот осей |
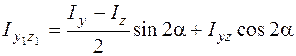. (5.22)
Угол в формулах (5.20)–(5.22), на что поворачиваются оси, считается хорошим, если он отсчитывается от хорошего направления оси к хорошему направлению оси . На рис. 5.14 угол .
Дабы отыскать, на какой угол нужно развернуть оси, дабы они стали главными осями инерции, положим в соответствии с определению основных осей центробежный момент инерции по (5.22) равным нулю. Тогда
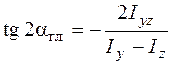. (5.23)
Подставляя отысканный угол в формулу (5.20), возможно взять формулу для определения моментов инерции относительно главных осей
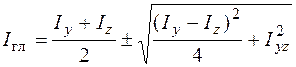. (5.24)
Моменты инерции относительно главных осей имеют экстремальные значения среди нескончаемого множества центральных осей: довольно одной оси момент инерции велик, довольно второй имеет минимальное значение. Дабы узнать, какой момент инерции: большой либо минимальный – имеет место для основной оси , развёрнутой на угол от оси , исследуем символ второй производной функции , определяемой формулой (5.20). Вычислим эту производную:
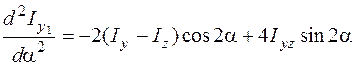. (5.25)
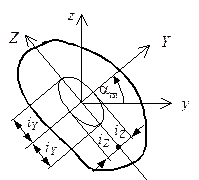 Рис. 5.15. Эллипс инерции |
В случае, если при вторая производная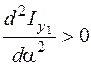 
, то относительно оси момент инерции минимален ( ), в случае, если 
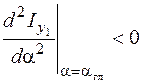, то .
По окончании определения моментов инерции относительно главных осей возможно выстроить эллипс инерции – эллипс, полуоси которого равны радиусам инерции относительно главных осей. Радиус инерции откладывается на протяжении основной оси , а – на протяжении оси (рис. 5.15). Построение эллипса инерции комфортно применять для анализа правильности определения моментов инерции. Эллипс инерции должен быть вытянут в том направлении, в котором вытянута фигура.
Подводя итог приведем кое-какие формулы для определения моментов несложных фигур довольно центральных осей. Для прямоугольника (рис. 5.16, а) оси , являются не только центральными, но и главными, моменты инерции довольно этих осей
; 
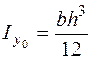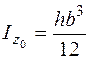; . (5.26)
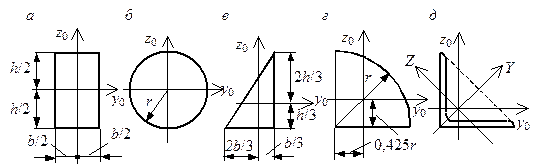 Рис. 5.16. К определению моментов инерций несложных фигур |
Для круга (рис. 5.16, б) каждая ось, проходящая через центр тяжести, есть основной и
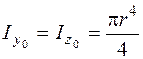; . (5.27)
У прямоугольного треугольника (рис. 5.16, в) оси , не являются главными, исходя из этого центробежный момент инерции довольно этих осей не равен нулю. Моменты инерции треугольника определяются по формулам
; 
; 
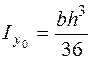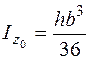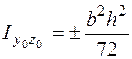. (5.28)
На рис. 5.16, г продемонстрирована фигура, воображающая собой четверть круга (квадрант круга). Для данной фигуры довольно центральных осей , моменты инерции
; 
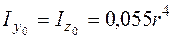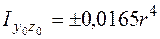. (5.29)
Дабы выяснить символ центробежного момента инерции треугольника либо квадранта круга, нужно применять следующее правило знаков: в случае, если гипотенуза треугольника (дуги квадранта) в совокупности координат , описывается возрастающей функцией, то центробежный момент инерции хорош. Для продемонстрированного на рис. 5.16, в треугольника , квадрант круга, изображенный на рис. 5.16, г, имеет отрицательный центробежный момент инерции.
При определении моментов инерции фигуры, складывающейся из прокатных профилей: двутавров, швеллеров, уголков (как в задаче № 31), осевые моменты инерции довольно собственных центральных осей двутавров, швеллеров, уголков берутся из таблиц прокатных профилей. Центробежные моменты швеллеров и инерции двутавров довольно собственных осей равны нулю. Центробежный момент инерции равнобоких уголков относительно осей , параллельных полкам, определяется по формуле
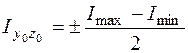, (5.29а)
где , – моменты инерции относительно главных центральных осей уголка (рис. 5.16, д) – находятся по таблице прокатных профилей. Выбор символа в формуле (5.29а) производится по аналогичной схеме, что и для треугольника либо квадранта круга: в случае, если линия, соединяющая крайние точки уголка (пунктир на рис. 5.16, д), описывается возрастающей функцией в совокупности координат , то . Для уголка на рис. 5.16, д центробежный момент инерции .
Примеры ответа задач
Пример 1. Определение моментов инерции сечения, имеющего одну ось симметрии
Условие задачи
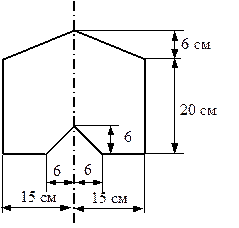 Рис. 5.17. Фигура с одной осью симметрии |
Сечение стержня воображающее собой фигуру, владеющую одной осью симметрии, продемонстрировано на рис. 5.17. Требуется отыскать моменты инерции данной фигуры относительно главных центральных осей.
Ответ
Ось – ось симметрии фигуры (рис. 5.18) – есть основной осью инерции. Отыщем положение второй основной центральной оси, выяснив положение центра тяжести фигуры. Разумеется, что центр тяжести лежит на оси симметрии, исходя из этого отыщем лишь координату по последней из формул (5.15). Разобьем сложную фигуру на составляющие простые: две пары прямоугольных треугольников I , III и прямоугольник II (см. рис. 5.18). Площадь фигуры
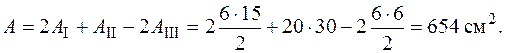
Для определения статического момента выберем запасного ось , проходящую через центр тяжести прямоугольника II. В этом случае статический момент фигуры II равен нулю. Дабы отыскать статические моменты треугольников, умножаем площадь фигуры на координату ее центра тяжести в совокупности :
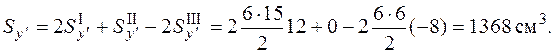
Тогда по (5.15)
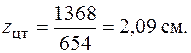
Откладываем эту координату и проводим через центр тяжести (точку С на рис. 5.18) основную центральную ось .
Отыщем моменты инерции всей фигуры относительно осей и , складывая (либо вычитая) моменты инерции составляющих фигур:
;
.
Для определения момента инерции каждой из фигур I, II и Ш используем формулы трансформации моментов инерций при параллельном переносе осей (5.16), (5.17). Моменты инерции прямоугольника II и треугольников I и Ш довольно собственных центральных осей (см. рис. 5.18) находим по формулам (5.26), (5.28). Тогда
 Рис. 5.18. К определению моментов инерции симметричной фигуры |
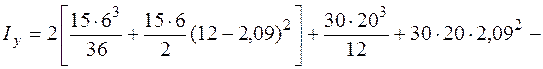
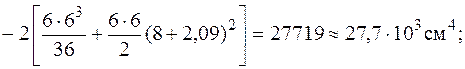
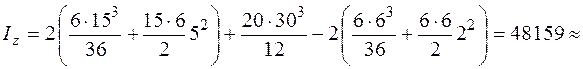
Подводя итог вычислим радиусы инерции относительно главных центральных осей по формулам (5.10) и выстроим эллипс инерции.
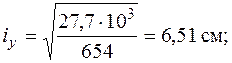
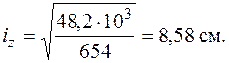
Эллипс инерции продемонстрирован на рис. 5.18.
Пример 2. Определение моментов инерции
Несимметричного сечения
Условие задачи
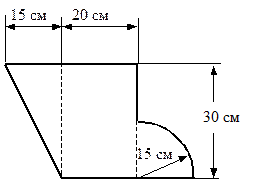 Рис. 5.19. Несимметричная фигура |
Сечение стержня представляет собой несимметричную фигуру, продемонстрированную на рис. 5.19. Требуется отыскать положение основных центральных осей инерции фигуры и моменты инерции довольно этих осей.
Ответ
Отыщем положение центра тяжести фигуры по формулам (5.15). Разобьем фигуру на три простые: треугольник I, прямоугольник II и квадрант круга Ш. Площадь всей фигуры
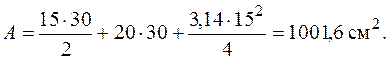
Для определения статических моментов выберем запасные оси , проходящие через центр тяжести прямоугольника II (рис. 5.20). Статический момент каждой фигуры равен площади фигуры, умноженной на координату центра тяжести данной фигуры в совокупности координат . Суммарные статические моменты
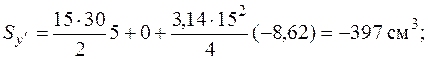
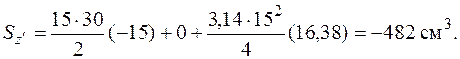
Координаты центра тяжести
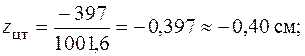
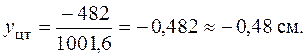
отложены на рис. 5.20.
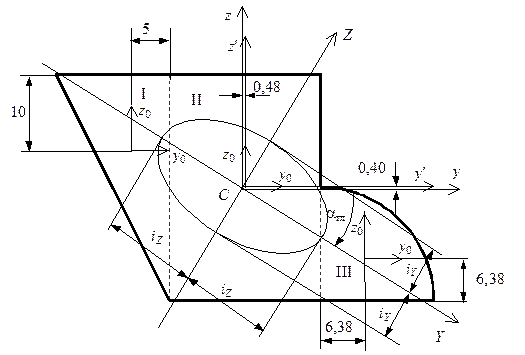 Рис. 5.20. К определению моментов инерции несимметричной фигуры |
Совершим через центр тяжести центральные оси (см. рис. 5.20) и отыщем моменты инерции довольно этих осей, как сумму моментов инерций несложных фигур, составляющих заданную фигуру. Для определения моментов инерции несложных фигур I, II и Ш используем формулы (5.16)–(5.18). Моменты инерции довольно собственных осей прямоугольника, квадранта и треугольника круга вычисляем по формулам (5.26), (5.28) и (5.29).
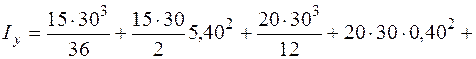
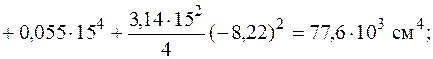
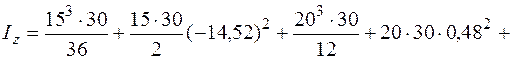
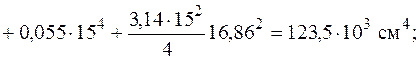
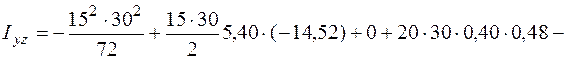
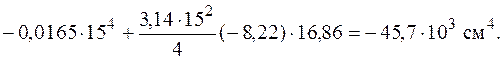
Сейчас отыщем положение основных осей инерции. Угол, на что нужно развернуть ось , дабы она стала основной осью, определяем по формуле (5.23):
;
; .
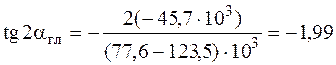В соответствии с правилом знаков откладываем отрицательный угол по часовой стрелке и проводим главные центральные оси инерции (см. рис. 5.20). Вычислим моменты инерции довольно этих осей по формуле (5.24):
; .
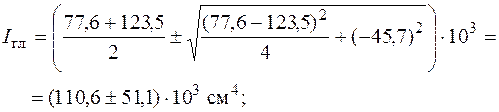
Для проверки вычислений комфортно применять следующее свойство: сумма моментов инерций довольно двух любых пар ортогональных осей имеется величина постоянная. Тогда должно быть
.
В отечественном примере .
Дабы узнать, какой момент инерции – большой либо минимальный – соответствует оси , исследуем символ второй производной функции по (5.25).
.
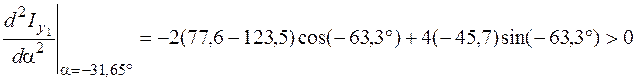Хороший символ второй производной свидетельствует, что оси соответствует минимальное значение момента инерции, т. е.
Отыщем радиусы инерции относительно главных центральных осей по (5.10) и выстроим эллипс инерции.
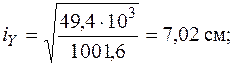
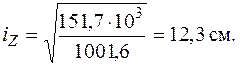
Эллипс инерции продемонстрирован на рис. 5.20. Видно, что эллипс вытянут в том направлении, в котором вытянута фигура.