ВВЕДЕНИЕ
Моделирование – это методика научной и практической деятельности людей, основанная на построении, использовании и исследовании моделей.
Моделирование решает исследования и задачи изучения объектов и совокупностей, предсказания их поведения и функционирования.
При управлении модели разрешают оценивать ненаблюдаемые переменные процесса функционирования совокупности, прогнозировать состояние процесса при имеющихся либо выбираемых управлениях и синтезировать стратегии и алгоритмы управления.
При эксплуатации и проектировании совокупностей появляются бессчётные задачи, требующие оценки количественных и качественных закономерностей процессов их функционирования, проведения структурного, алгоритмического и параметрического синтеза. Ответ этих неприятностей нереально без применения математического моделирования, что обусловлено изюминками громадных совокупностей, такими как сложность структур, стохастичность связей между внешней средой и элементами, неоднозначность методов поведения, много параметров и переменных, неполнота и недетерминированность исходной информации. Математическое моделирование разрешает значительно уменьшить время проектирования, во многих случаях разрешает отыскать оптимальное ответ, исключить способ натурных ошибок и проб, перейти к параллельному процессу проектирования.
Математическая модель представляет собой формализованное описание совокупности на некоем абстрактном языке, к примеру, в виде совокупности математических соотношений либо метода. Конкретно математические модели рассматриваются как главный инструмент оценки эффективности других ответов.
С развитием вычислительной техники самый эффективным и универсальным способом изучения совокупностей стало компьютерное (машинное) моделирование, сущность которого пребывает в проведении на ЭВМ опытов с моделью, являющейся программный комплекс, обрисовывающий формально и алгоритмически поведение элементов совокупности в ходе её функционирования, т.е. их сотрудничество между собой и внешней средой.
Краткое изложение баз теории моделирования есть главной задачей данного учебного пособия.
“Определите значения слов,
И вы избавите человечество
От половины его заблуждений”.
Р.Декарт
Правила подхода в моделировании совокупностей
В моделировании совокупностей употребляются хороший (индуктивный) и системный (дедуктивный) подходы [8].
Хороший подход разглядывает исследуемую совокупность с позиций делаемых функций (функциональный подход) и предполагает создание модели путём перехода от частного к неспециализированному слиянием её отдельных компонент, разрабатываемых раздельно.
Процесс синтеза модели на базе хорошего подхода схематично представлен на рис. 1.2 и включает следующие этапы:
1. Декомпозиция настоящей совокупности, подлежащей моделированию, на отдельные системы.
2. Выбор данных для моделирования, включающих:
– назначение;
– условия работы;
– окружающую среду;
– ограничения.
3. Постановка целей, отображающих отдельные стороны процесса моделирования совокупности.
4. Формирование на базе целей и данных компонент будущей модели.
5. Совокупность компонент объединяется в модель.
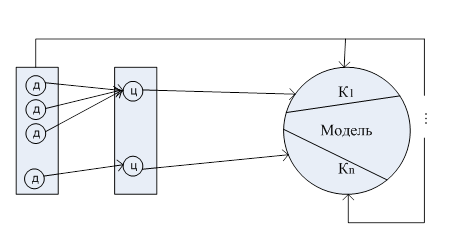
Рис. 1.2. Процесс синтеза модели на базе хорошего подхода:
Д – данные; Ц – цели; К – компонента модели
Так, разработка модели на базе хорошего подхода свидетельствует суммирование отдельных компонент в единую модель, причём любая из компонент решает собственные задачи и изолирована от вторых частей модели. Исходя из этого хороший подход возможно использован для реализации относительно несложных моделей, в которых допустимо разделение и взаимно свободное рассмотрение отдельных сторон функционирования настоящего объекта.
Системный подход разглядывает исследуемую совокупность в виде целенаправленного множества взаимосвязанных элементов (структурный подход) и предполагает создание модели путём перехода от общего к частному, в то время, когда в базе рассмотрения лежит цель, наряду с этим исследуемый объект выделяется из экологии.
Процесс синтеза модели на базе системного подхода схематично представлен на рис. 1.3 и включает следующие этапы:
1. На базе цели функционирования совокупности, которая определяется вопросами, на каковые исследователь желает узнать ответы посредством модели, и данных, включающих назначение модели, условия работы совокупности, окружающую среду для совокупности и накладываемые ограничения, формируются требования к модели совокупности.
2. Определение систем модели на базе организованных требований.
3. Подбор элементов систем модели на базе данных для их реализации.
4. Выбор составляющих элементов будущей модели на базе организованных параметров выбора.
5. Оказавшаяся так модель есть интегрированным целым.
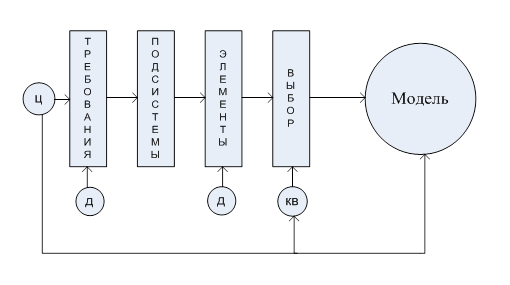
Рис. 1.3. Процесс синтеза модели на базе системного подхода:
Ц – цель моделирования; Д – данные; КВ – критерии выбора
Системный подход разрешает решить проблему построения модели сложной совокупности с учетом всех взаимосвязей и факторов, пропорциональности их значимости на построения модели исследования и всех этапах системы. Системный подход свидетельствует, что любая совокупность есть интегрированным целым кроме того тогда, в то время, когда она складывается из отдельных разобщённых систем.
Так, в базе системного подхода лежит рассмотрение совокупности как интегрированного целого, причём это рассмотрение при разработке начинается с главного: формулировки цели функционирования.
На данный момент при синтезе и анализе громадных совокупностей взял распространение системный подход, что разрешает учитывать сложные стохастические связи в совокупности и сотрудничество с внешней средой. Модель в этом случае создается под поставленную проблему, а моделирование содержится в ответе неприятности цели, неприятности построения модели, неприятности работы с моделью. Для верно выбранной модели характерным есть то, что она выявляет только те закономерности, каковые необходимы исследователю, и не рассматривает свойства совокупности, не значительные для данного изучения.
При имитационном моделировании в качестве имитационной модели выступает метод, воспроизводящий процесс функционирования исследуемой совокупности, наряду с этим имитируются элементарные явления составляющего процесса, с сохранением их последовательности протекания и логической структуры во времени, что разрешает по исходным разрешённым получить сведения о состояниях процесса в определённые моменты времени, дающие возможность оценить характеристики совокупности. Компьютер при имитационном моделировании является имитатором исследуемой совокупности
Главным преимуществом имитационного моделирования если сравнивать с аналитическим есть возможность ответа более непростых задач. Способ имитационного моделирования разрешает решать задачи анализа громадных совокупностей, включая задачи оценки: вариантов структуры совокупности, эффективности разных методов управления совокупностью, влияния трансформации параметров совокупности. Имитационное моделирование возможно положено кроме этого в базу структурного, алгоритмического и параметрического синтеза громадных совокупностей, в то время, когда требуется создать совокупность с заданными чертями при определённых ограничениях, которая есть оптимальной по выбранным параметрам оценки эффективности.
Комбинированное (аналитико-имитационное) моделирование при синтезе и анализе совокупностей разрешает объединить преимущества аналитического и имитационного моделирования. При построении комбинированных моделей проводится декомпозиция процесса функционирования объекта на составляющие подпроцессы, и для тех из них, где это быть может, употребляются аналитические модели, а для остальных подпроцессов строятся имитационные модели. Таковой комбинированный подход разрешает охватить как следует новые классы совокупностей, каковые не смогут быть изучены с применением лишь аналитического и имитационного моделирования в отдельности.
При настоящем моделировании употребляется возможность изучения разных черт или на настоящим объекте полностью, или на его части. Отличие опыта от настоящего протекания процесса содержится в том, что в нём смогут показаться отдельные критические обстановки. На протяжении опыта вводятся новые факторы и раздражающие действия в ходе функционирования объекта.
Настоящее моделирование подразделяется на натурное и физическое.
Натурным моделированием именуют проведение изучения на настоящем объекте с последующей обработкой результатов опыта на базе теории подобия. При функционировании объекта в соответствии с поставленной целью удаётся распознать закономерности протекания настоящего процесса. Разновидности натурного моделирования, как комплексные опробования, производственный и натурный эксперимент , владеют высокой степенью достоверности.
Физическое моделирование отличается от натурного тем, что изучение проводится на установках, каковые сохраняют природу явлений и владеют физическим подобием. В ходе физического моделирования задаются кое-какие характеристики окружающей среды и исследуется поведение или настоящего объекта, или его модели при заданных либо создаваемых искусственно действиях окружающей среды. Физическое моделирование может протекать в настоящем и нереальном (псевдореальном) масштабах времени, и может рассматриваться без учёта времени.
Настоящее моделирование есть самоё адекватным, но наряду с этим его возможности с учётом изюминок настоящих объектов ограничены.
С позиций математического описания объекта и в зависимости от его характера модели возможно поделить на модели аналоговые (постоянные), цифровые (дискретные) и аналого-цифровые (комбинированные). Под аналоговой моделью понимается модель, которая описывается уравнениями, связывающими постоянные размеры. Под цифровой понимается модель, которая описывается уравнениями, связывающими дискретные размеры, представленные в цифровом виде. Под аналого-цифровой понимается модель, которая возможно обрисована уравнениями, связывающими постоянные и дискретные размеры.
Особенный вид моделирования – кибернетическое моделирование, в котором отсутствует яркое подобие между моделью и реальным объектом. В этом случае стремятся отобразить только некую функцию и разглядывают настоящий объект как “тёмный ящик”, имеющий последовательность выходов и входов, и моделируются кое-какие связи между входами и выходами. Значительно чаще при применении кибернетических моделей выполняют анализ поведенческой стороны объекта при разных действиях окружающей среды. Так, в базе кибернетических моделей лежит отношение некоторых информационных процессов управления, что разрешает оценить поведение настоящего объекта.
“Высшее назначение математики —
Обнаружить порядок в хаосе,
Что нас окружает “.
Н.Винер
Т а б л и ц а 2.1
Таблица входов и переходов автомата Мили
| Входы xi | Состояния zk | |||||
| z0 | z1 | … | … | … | zk | |
| Переходы | ||||||
| x1 | ?(z0, x1) | ?(z1, x1) | … | … | … | ?(zk,x1) |
| x2 | ?(z0, x2) | ?(z1, x2) | … | … | … | ?(zk,x2) |
| …. | ….. | …. | …. | …. | …. | …. |
| Выходы | ||||||
| x1 | ?(z0, x1) | ?(z1, x1) | … | … | … | ?(zk,x1) |
| x2 | ?(z0, x2) | ?(z1, x2) | … | … | … | ?(zk,x2) |
| …. | ….. | …. | …. | …. | …. | …. |
Т а б л и ц а 2.2
Таблица входов и переходов автомата Мили с тремя состояниями (светло синий0, z1, z2), двумя входными (x1, x2) и двумя выходными (y1, y2) сигналами
| Входы xi | Состояния zk | ||
| z0 | z1 | z2 | |
| Переходы | |||
| x1 | z2 | z0 | z0 |
| x2 | z0 | z2 | z1 |
| Выходы | |||
| x1 | y1 | y1 | y2 |
| x2 | y1 | y2 | y1 |
Описание работы F–автоматов Мура иллюстрируется таблицей 2.3, а пример табличного метода задания F–автомата Мура с пятью состояниями (z0, z1, z2, z3, z4), двумя входными (x1, x2) и тремя выходными (y1, y2, y3) сигналами приведён в таблице 2.4.
Графический метод задания конечного автомата применяет понятие направленного графа. Граф автомата является набором вершин, соответствующих разным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем либо иным переходам автомата. В случае, если входной сигнал xk приводит к переходу из состояния zi в состояние zj, то на графе автомата дуга, соединяющая вершину zi с вершиной zj, обозначается xk. Чтобы задать функцию выходов, дуги графа нужно отметить соответствующими выходными сигналами.
Т а б л и ц а 2.3
Отмеченная таблица переходов автомата Мура
| Входы xi | Состояния zk | |||
| ?(z0) | ?(z1) | …. | ?(zk) | |
| z0 | z1 | …. | zk | |
| x1 | ?(z0, x1) | ?(z1, x1) | … | ?(zk,x1) |
| x2 | ?(z0, x2) | ?(z1, x2) | … | ?(zk,x2) |
| … | … | … | … | … |
Т а б л и ц а 2.4
Отмеченная таблица переходов автомата Мура с пятью состояниями (z0, z1, z2, z3, z4), двумя входными (x1, x2) и тремя выходными (y1, y2, y3) сигналами
| Входы xi | Состояния zk | ||||
| y1 | y1 | y3 | y2 | y3 | |
| z0 | z1 | z2 | z3 | z4 | |
| x1 | z1 | z4 | z4 | z2 | z2 |
| x2 | z3 | z1 | z1 | z0 | z0 |
Для автоматов Мили эта разметка производится так: в случае, если входной сигнал xk действует на состояние zi, то, в соответствии с сообщённому, получается дуга, исходящая из zi и помеченная xk; эту дугу дополнительно отмечают выходным знаком y = ?(zi, xk). На рис. 2.3 приведён заданный ранее таблицей 2.2 граф F–автомата Мили.
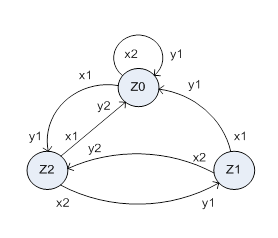
Рис. 2.3. Граф автомата Мили
Для автоматов Мура подобная разметка графа такова: в случае, если входной сигнал xk, действуя на некое состояние zi автомата, приводит к переходу в состояние zj, то дугу, направленную в zj и помеченную xk, дополнительно отмечают выходным знаком y = ?(zj, xk). На рис. 2.4 приведён заданный ранее таблицей 2.4 граф F–автомата Мура.
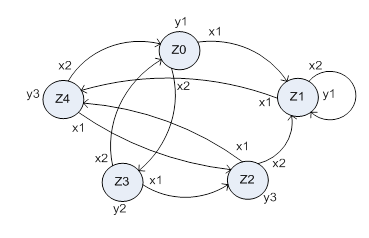
Рис. 2.4. Граф автомата Мура
Матричный метод задания конечного автомата довольно часто есть более эргономичной формой. Наряду с этим матрица соединений автомата имеется квадратная матрица C = [cij], строки которой соответствуют исходным состояниям, а столбцы – состояниям перехода.
При F–автомата Мили элемент cij = xk/ys, стоящий на пересечении i-ой строки и j-го столбца, соответствует входному сигналу xk, привёдшему к переходу из состояния zi в состояние zj, и выходному сигналу ys, выдаваемому наряду с этим переходе. Для автомата Мили, рассмотренного выше, матрица соединений имеет форму
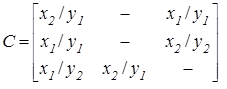 . (2.9)
. (2.9)
В случае, если переход из состояния zi в состояние zj происходит под действием нескольких сигналов, элемент матрицы cij является множеством пар «вход-выход» для этого перехода, соединённых знаком дизъюнкции.
Для F–автомата Мура элемент cij = xk/ys равен множеству входных сигналов на переходе (zi, zj), а выход описывается вектором выходов, i-я компонента которого – выходной сигнал, отмечающий состояние zi. Для автомата Мура, рассмотренного выше, вектор выходов и матрица соединений имеют вид
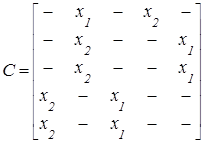 ;
; 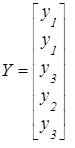 . (2.10)
. (2.10)
Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некоем состоянии, под действием любого входного сигнала не имеет возможности перейти более чем в одно состояние. Это указывает, что в графе автомата из любой вершины не смогут выходить две и более дуг, отмеченных одним и тем же входным знаком, а в матрице соединений в каждой строке входной сигнал не должен видеться более одного раза.
Разглядим граф и таблицу переходов асинхронного конечного автомата. Для F–автомата состояние zk именуется устойчивым, в случае, если для любого входа xi I X, для которого ?(zk, xi) = zk имеет место ?(zk, xi) = yk. Так, F–автомат именуется асинхронным, в случае, если каждое его состояние zk I Z устойчиво.
Ниже приведён пример асинхронного автомата Мура, заданного таблично (табл.2.5) и графически (рис.2.5).
Т а б л и ц а 2.5
Отмеченная таблица переходов асинхронного автомата Мура с тремя состояниями (z0, z1, z2), тремя входными (x1, x2, x3) и тремя выходными (1y, y2, y3) сигналами
| xi | yk | ||
| y1 | y3 | y2 | |
| z0 | z1 | z2 | |
| x1 | z2 | z2 | z2 |
| x2 | z1 | z1 | z2 |
| x3 | z0 | z1 | z0 |
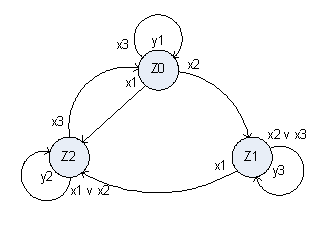
Рис. 2.5. Граф асинхронного автомата Мура
В таблице переходов асинхронного автомата некое состояние zk стоит на пересечении строчка xi и столбца zs (s ¹ k), и это состояние zk непременно должно встретиться в данной же строке в столбце zk. В графе асинхронного автомата, в случае, если в некое состояние имеются переходы из вторых состояний под действием каких-то сигналов, то в вершине zk должна быть петля, отмеченная знаками тех же входных сигналов.
Понятие F–автоматаявляется математической абстракцией, удобной для описания широкого класса процессов функционирования настоящих объектов, для которых характерно наличие дискретных состояний и дискретный темперамент работы во времени. Но широта применения не свидетельствует универсальности F–схем. Данный подход не пригоден для описания процессов в динамических совокупностях с наличием переходных процессов, для формализации которых употребляются решётчатые функции и разностные уравнения, Z–описание и преобразование в пространстве состояний [14].
2.3.3. Дискретно-стохастические модели (P–схемы)
Применение P–схем разрешает формализовать процесс функционирования дискретных совокупностей, проявляющих статистически закономерное случайное поведение.
Вероятностный автомат (англ. Probabilistic Automata) определяется как дискретный потактовый преобразователь информации с памятью, функционирование которого в каждом такте зависит лишь от состояния памяти в нём и возможно обрисовано статистически [8].
Использование схем вероятностных автоматов (P–схем) имеет серьёзное значение для разработки способов проектирования дискретных совокупностей, проявляющих статистически закономерное случайное поведение, для выяснения алгоритмических возможностей таких обоснования и систем границ целесообразности их применения, и для ответа задач синтеза по выбранному критерию дискретных стохастических совокупностей, удовлетворяющих заданным ограничениям.
Введём математическое понятие P–автомата, применяя понятия, введённые для F–автомата. Разглядим множество G, элементами которого являются всевозможные пары (xi, zs), где xi и zs – элементы входного множества X и множества состояний Z соответственно. В случае, если существуют две такие функции ? и ?, что с их помощью осуществляются отображения G®Z и G®Y, то говорят, что F = X, Y, Z, ?, ?, z0 определяет автомат детерминированного типа.
Введём в рассмотрение более неспециализированную математическую схему. Пускай Ф – множество всевозможных пар вида (zk, yj), где yj – элементы выходного множества Y. Потребуем, дабы любой элемент множества G индуцировал на множестве Ф некий закон распределения следующего вида:
| Элементы из Ф (xi, zs) | … … | (z1, y1) b11 | (z1, y2) b12 | … … | (zK, yJ-1) bK(J-1) | (zK, yJ) bKJ |
Наряду с этим 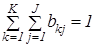 , где bkj – возможность перехода автомата в состояние zk и появления на выходе сигнала yj, если он был в состоянии zs, и на его вход сейчас времени поступил сигнал xi. Число таких распределений, представленных в виде таблиц, равно элементов множества G. Обозначим множество этих таблиц через B. Тогда четвёрка элементов P = X, Y, Z, B именуется вероятностным автоматом (P–автоматом).
, где bkj – возможность перехода автомата в состояние zk и появления на выходе сигнала yj, если он был в состоянии zs, и на его вход сейчас времени поступил сигнал xi. Число таких распределений, представленных в виде таблиц, равно элементов множества G. Обозначим множество этих таблиц через B. Тогда четвёрка элементов P = X, Y, Z, B именуется вероятностным автоматом (P–автоматом).
Пускай элементы множества G индуцируют кое-какие законы распределения на множествах Y и Z, что возможно представить соответственно в виде:
| Элементы из Y (xi, zs) | … … | y1 q1 | y2 q2 | … … | yJ-1 qJ-1 | yJ qJ |
| Элементы из Z (xi, zs) | … … | z1 z1 | z2 z2 | … … | zK-1 zK-1 | zK zK |
Наряду с этим 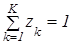 и
и 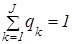 , где zk и qk – возможности перехода P–автомата в состояние zk и появление выходного сигнала yk при условии, что P–автомат был в состоянии zs и на его вход поступил входной сигнал xi.
, где zk и qk – возможности перехода P–автомата в состояние zk и появление выходного сигнала yk при условии, что P–автомат был в состоянии zs и на его вход поступил входной сигнал xi.
В случае, если для всех k и j имеет место соотношение qkzj = bkj, то таковой P–автомат именуется вероятностным автоматом Мили. Это требование свидетельствует исполнение условия независимости распределений для нового состояния P–его выходного и автомата сигнала.
Пускай сейчас определение выходного сигнала P–автомата зависит только от того состояния, в котором был автомат в данном такте работы. Иначе говоря пускай любой элемент выходного множества Y индуцирует распределения возможностей выходов, имеющих следующий вид:
| Элементы из Y zk | … … | y1 s1 | y2 s2 | … … | yK-1 sI-1 | yK sI |
Тут 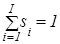 , где si – возможность появления выходного сигнала yi при условии, что P–автомат был в состоянии zk.
, где si – возможность появления выходного сигнала yi при условии, что P–автомат был в состоянии zk.
В случае, если для всех k и i имеет место соотношение zksi = bki, то таковой P–автомат именуется вероятностным автоматом Мура. Понятие P–автоматовМили и Мура введено по аналогии с детерминированным F–автоматом.
Частным случаем P–автомата, задаваемого как P = X, Y, Z, B , являются автоматы, у которых или переход в новое состояние, или выходной сигнал определяются детерминированно. В случае, если выходной сигнал P–автоматаопределяется детерминированно, то таковой автомат именуется Y–детерминированным вероятностным автоматом. Подобно, Z–детерминированным вероятностным автоматом именуется P–автомат, у которого выбор нового состояния есть детерминированным.
Методы задания работы P–автоматовтакие же, как и для F–автоматов.
Как пример разглядим Y–детерминированный вероятностный автомат, заданный таблицей переходов (табл. 2.6) и таблицей выходов (табл.2.7). До начала работы P–автоматвсегда будет в начальном состоянии z0 и в нулевой такт времени начинает изменять собственное состояние в соответствии с заданным распределением.
Т а б л и ц а 2.6
Таблица переходов Y–детерминированного вероятностного автомата
| zj zi . | zj | ||||
| z0 | z1 | z2 | z3 | z4 | |
| z0 z1 z2 z3 z4 | 0.5 | 0.75 0.4 | 0.5 0.25 0.6 |
Т а б л и ц а 2.7
Таблица выходов Y–детерминированного вероятностного автомата
| Z | z0 | z1 | z2 | z3 | z4 |
| Y |
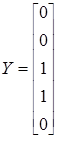
Для разглядываемого P–автомата вектор выходов и матрица соединений имеют вид
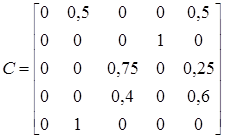 ;
;  . (2.11)
. (2.11)
В матрице соединений Y–детерминированного вероятностного автомата элемент cij = pij определяется возможностью перехода P–автомата в состояние zj из состояния zi при поступлении входного сигнала, а выход описывается вектором выходов, i-я компонента которого – выходной сигнал, отмечающий состояние zi.
Обрисованный Y–детерминированный P–автомат возможно задать в виде ориентированного графа (рис. 2.6), вершины которого сопоставляются состояниям автомата, а дуги – вероятным переходам из одного состояния в второе. Дуги имеют веса, соответствующие возможностям перехода pij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями.
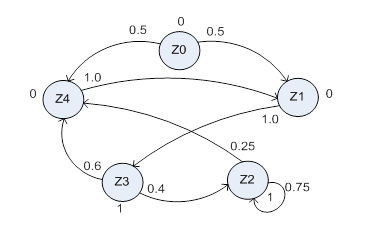
Рис. 2.6. Граф Y–детерминированного вероятностного автомата
Оценим суммарную финальную возможность нахождения этого P–автомата в состояниях z2 и z3. Наряду с этим начальное состояние z0 возможно не учитывать, поскольку начальное распределение не оказывает влияния на значения финальных возможностей. Тогда матрица возможностей перехода автомата будет иметь вид
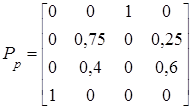 ,
,
откуда приобретаем совокупность уравнений, определяющих возможности финального нахождения автомата в состояниях pj ( )
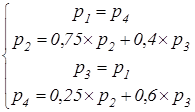 .
.
Добавим к этим уравнениям условие нормировки p1 + p2 + p3 + p4 = 1.
Тогда, решая совокупность уравнений, возьмём p1 = p3 = p4 = 5/23, p2 = 8/23. Так, p2 + p3 = 13/23 = 0,5652. Иначе говоря при нескончаемой работе заданного в этом примере Y–детерминированного вероятностного автомата на его выходе формируется бинарная последовательность с возможностью появления единицы, равной 0,5652.
Для оценки разных черт исследуемых совокупностей, представленных в виде P–схем, не считая рассмотренного случая аналитических моделей, возможно использовать и имитационные модели, реализуемые, к примеру, способом статистического моделирования.
2.3.4. Непрерывно-стохастические модели (Q–схемы)
Применение Q–схем разрешает формализовать процессы функционирования совокупностей, каковые, по собственной сути, являются процессами обслуживания.
Q–схемы используются в качестве типовых математических схем совокупностей массового обслуживания (англ. Queueing System) [8].
В качестве процесса обслуживания смогут быть представлены разные по собственной физической природе процессы функционирования экономических, производственных, технических и других систем, к примеру: потоки поставок продукции предприятию, потоки комплектующих и деталей изделий на сборочном конвейере цеха, заявки на обработку информации ЭВМ от удалённых терминалов и т.д. Характерным для работы аналогичных объектов есть стохастический темперамент процесса их функционирования, проявляющийся:
– в случайном появлении заявок (требований) на обслуживание;
– в завершении обслуживания в случайные моменты времени.
Разглядим главные понятия совокупностей массового обслуживания (СМО), нужные для применения Q–схем, как при аналитическом, так и при имитационном подходе.
Элементы СМО. В СМО фигурируют:
1. Средства обслуживания – обслуживающие аппараты (ОА) либо каналы обслуживания (К). Средства обслуживания являются статическими элементами Q–схем.
2. Обслуживаемые заявки – транзакты. Являются динамическими элементами Q–схем.
3. Очереди.
Состояние СМО характеризуется:
1. Состояниями всех обслуживающих аппаратов, любой из которых может быть в состоянии “занят” либо “свободен”.
2. Состояниями всех транзактов, любой из которых может быть в состоянии “обслуживание” либо “ожидание”.
3. Состояниями всех очередей к обслуживающим аппаратам, определяемыми числом находящихся в них транзактов.
Переменные СМО. Переменные размеры разделяются на свободные и системные.
Свободные размеры СМО характеризуются двумя случайными переменными:
а) промежуток прибытия – промежуток времени между последовательными моментами прибытия заявок в совокупность;
б) время обслуживания – время, требуемое обслуживающему аппарату для исполнения обслуживания.
Системные размеры СМО являются предметом изучения совокупности и назначаются исследователем, к примеру:
а) число заявок, прибывших на обслуживание за заданный временной отрезок;
б) число заявок, каковые попали на обслуживание сразу же по прибытии;
в) среднее время нахождения заявок в очереди;
г) средние длины очередей;
д) большая протяженность очереди;
е) нагрузка обслуживающего аппарата, являющаяся функцией времени, которое израсходовано ОА на обслуживание в течение заданного промежутка времени и т.д.
На рис. 2.7 приведён пример совокупности обслуживания одним очередью и обслуживающим аппаратом. Совокупность функционирует следующим образом. Заявка из источника заявок приходит на обслуживание. В случае, если обслуживающий аппарат свободен, то заявка занимает его, и начинается процесс обслуживания. В случае, если обслуживающий аппарат занят, то заявка поступает в очередь, где ожидает окончания обслуживания прошлой заявки. Обслуженная заявка освобождает обслуживающий аппарат и покидает совокупность. Заявки, приходящие на обслуживание, образуют поток заявок; заявки, поступающие на обслуживание, образуют поток обслуживания; а заявки, покидающие совокупность по окончании обслуживания, образуют выходной поток. Эти потоки характеризуются интенсивностью l прихода заявок на обслуживание, интенсивностью m обслуживания и интенсивностью h ухода заявок из совокупности.
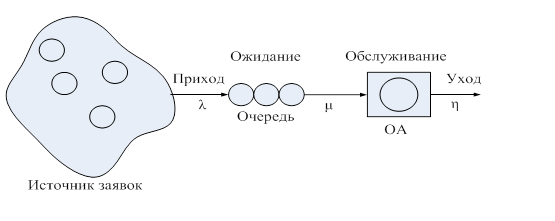
Рис. 2.7. Совокупность обслуживания одним очередью и обслуживающим аппаратом
Для графического изображения СМО введена символика Q–схем. Для начертания Q–схем употребляются следующие главные элементы.
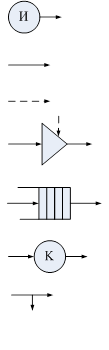 |
1. Источник заявок;
2. Материальные потоки (перемещение транзактов);
3. Информационные потоки (управляющие сигналы);
4. Клапан;
5. Накопитель;
6. Канал обслуживания;
7. Узел ? правило, в соответствии с которым
направляются транзакты.
Как пример графического изображения Q–схемы на рис. 2.8 приведена совокупность обслуживания со страховым заделом.
Перемещение заявок через Q–схему представляет собой материальные потоки. А для управления совокупности обслуживания употребляются информационные потоки.
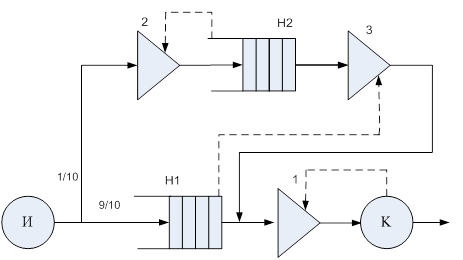
Рис. 2.8. Совокупность обслуживания со страховым заделом:
И – источник заявок; Н1 и Н2 – накопители; К – канал обслуживания;
1, 2, 3 – клапаны
Все трансформации, происходящие в совокупности, характеризуются событиями, каковые образуют потоки событий.
Потоком событий именуется последовательность событий, происходящих одно за вторым в случайные моменты времени. Различают следующие потоки событий [8].
Поток однородных событий – это поток, что характеризуется лишь моментами поступления этих событий (вызывающими моментами) и задаётся последовательностью {tn} = {0 ? t1 ? t2 ?…? tn ?…}, где – момент наступления n–го события – неотрицательное вещественное