Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: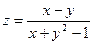 
.
Ответ. Разумеется, аналитическое выражение, задающее данную функцию, имеет суть тогда и лишь тогда, в то время, когда знаменатель дроби не равен нулю: . Уравнение задаёт на координатной плоскости параболу , вершина которой находится в точке , ветви направлены влево, а осью симметрии есть ось абсцисс. Так, областью определения данной функции являются все точки координатной плоскости, не считая тех, что лежат на параболе .
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1. .
Ответ.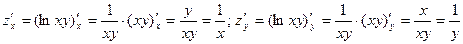 
.
2.2. .
Ответ. .
2.3. .
Ответ.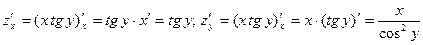 
.
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Ответ. Сперва отыщем частные производные первого порядка:
.
Сейчас находим производные второго порядка по переменным и :
.
Находим смешанные производные:
.
Задание 4. Отыскать производную функции в точке по направлению вектора .
Ответ. Производная функции по направлению вектора равна:
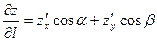, где направляющие косинусы вектора .
Находим частные производные данной функции:
.
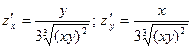Находим значения частных производных в точке :
.
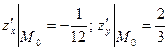Находим направляющие косинусы вектора :
.
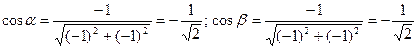Совсем возьмём:
.
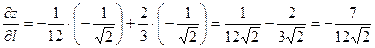Задание 5. Отыскать градиент функции в точке .
Ответ. Градиент функции двух переменных равен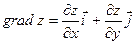 
.
Отыщем частные производные:
.
Определим значения частных производных в точке :
.
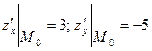Тогда градиент равен .
Задание 6. Изучить функцию на экстремумы.
Ответ. Областью определения данной функции есть вся числовая плоскость . Отыщем частные производные данной функции:
.
Производные первого порядка постоянны на всей области определения функции. Чтобы отыскать стационарные критические точки функции, решим совокупность уравнений:
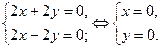
Взяли одну стационарную критическую точку . Чтобы узнать, есть ли она точкой экстремума, отыщем производные второго порядка.
.
Отыщем дискриминант: где .
В этом случае, . В данной точке экстремума нет.
Задание 7. Отыскать экстремум функции при условии .
Ответ. Областью определения данной функции есть вся числовая плоскость . Выразим из уравнения связи переменную : . Потом разглядим оба вероятных случая.
1) . Подставляя это выражение в исходную функцию, возьмём функцию одной переменной . Исследуем эту функцию на громаднейшее и мельчайшее значение при .
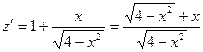. Разумеется, при любых значениях переменной , и исходя из этого громаднейшее и мельчайшее значение достигается в финишах отрезка.
.
2) . Подставляя это выражение в исходную функцию, возьмём функцию одной переменной . Исследуем эту функцию на громаднейшее и мельчайшее значение при .
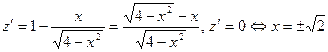. Взяли две стационарные критические точки. Определим значения функции в этих точках и на финишах отрезка.
.
Так, .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Ответ. В первую очередь, увидим, что эта функция постоянна в разглядываемой области. Отыщем стационарные критические точки функции, находящиеся в собствености указанной области. Частные производные первого порядка постоянны в данной области. Составим совокупность уравнений:
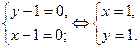
Взяли одну стационарную критическую точку . Определим значение функции в данной точке: . Потом, последовательно определим значения функции на всех границах области.
1) . Функция принимает вид . Тогда .
2) . Функция принимает вид . Тогда .
3) . Функция принимает вид . Тогда .
4) . Функция принимает вид . Тогда .
Взяли:
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения
Ответ. Воспользуемся приближённым равенством .
Из этого .
Разглядим функцию . Отыщем полный дифференциал данной функции:
.
Примем . Тогда возьмём:
. (Вычисление посредством микрокалькулятора даёт итог 7,916).
Вариант № 1
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: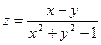 
.
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1. ; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции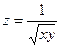 
в точке по направлению вектора .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения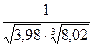 
.
Вариант № 2
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: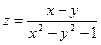 
.
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1. ; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции в точке по направлению вектора .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения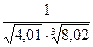 
.
Вариант № 3
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: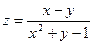 
.
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1. ; 2.2.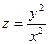 
; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции в точке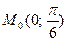 
по направлению вектора .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
Вариант № 4
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: .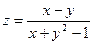
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1.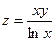 
; 2.2. 
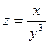; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции в точке по направлению вектора .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
Вариант № 5
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: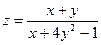 
.
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1. ; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции 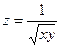в точке по направлению вектора .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения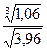 
.
Вариант № 6
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1.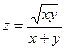 
; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции 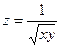в точке в направлении, составляющем с осью абсцисс угол .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
Вариант № 7
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1.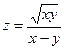 
; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции 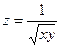в точке в направлении, составляющем с осью абсцисс угол .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
Вариант № 8
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1.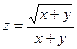 
; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции 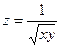в точке в направлении, составляющем с осью абсцисс угол .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
Вариант № 9
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1.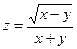 
; 2.2. ; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: .
Задание 4. Отыскать производную функции в точке в направлении, составляющем с осью абсцисс угол .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции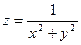 
в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
Вариант № 1.
Задание 1. Отыскать и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Отыскать частные производные первого порядка функций двух переменных:
2.1.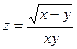 
; 2.2. 
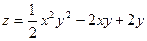; 2.3. .
Задание 3. Отыскать все частные производные второго порядка функции двух переменных: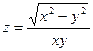 
.
Задание 4. Отыскать производную функции 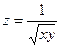в точке в направлении, составляющем с осью абсцисс угол .
Задание 5. Отыскать градиент функции в точке .
Задание 6. Изучить функцию на экстремумы.
Задание 7. Отыскать экстремум функции при условии .
Задание 8. Отыскать громаднейшее и мельчайшее значение функции в области .
Задание 9. Отыскать посредством полного дифференциала приближённое значение выражения .
ТИПОВОЙ РАСЧЁТ № 4
Теория возможностей