Многомерная матрица В=А-1 именуется обратной по отношению к гиперквадратной матрице А=(р,р), в случае, если выполняются следующие соотношения:
А(р,р)?В = В?А(р,р) = Е(р,р). (1.2)
Обратная многомерная матрица существует тогда и лишь тогда, в то время, когда определитель исходной гиперквадратной матрицы отличен от нуля. Численное обращение гиперквадратной матрицы может осуществляться методом плоского обращения ее двумерного табличного представления.
Псевдообратной многомерной матрицей В(g,p) = A+( g,p) по отношению к матрице А(р,g) именуется матрица В, удовлетворяющая следующим аналогам условий Мура-Пенроуза :
a) A(p,g)B(g,p)A(p,g) = A(p,g);
б) B(g,p)A(p,g)B(g,p) = B(g,p);
в)[B(g,p)A(p,g)]T = B(g,p)A(p,g);
г) [A(p,g)B(g,p)]T = A(p,g)B(g,p).
Псевдообратная матрица постоянно существует, и ее табличное представление сходится с результатом псевдообращения двумерного табличного представления исходной матрицы. Наряду с этим выполняется условие – в случае, если обратная матрица существует, то она сходится с псевдообратной: A+(p,g) = A-1(p,g).
Так, неспециализированное правило получения обратной матрицы возможно записать следующим образом.
1. Обратная матрица строится на базе обращения (псевдо-обращения) ее табличного представления.
2. Индексы обратной матрицы находятся так же, как при транспонировании матрицы. Выстроенная так матрица определяет структуру обратной матрицы, а значения ее элементов устанавливаются по табличному представлению обратной матрицы.Примечание. Многомерные обратные матрицы смогут употребляться для представления ответа линейных многомерно-матричных уравнений типа А(р,р)?Х(р,0)=В(р,0), которое дается соотношением: Х(р,0) =А-1(р,р)?В(р,0).
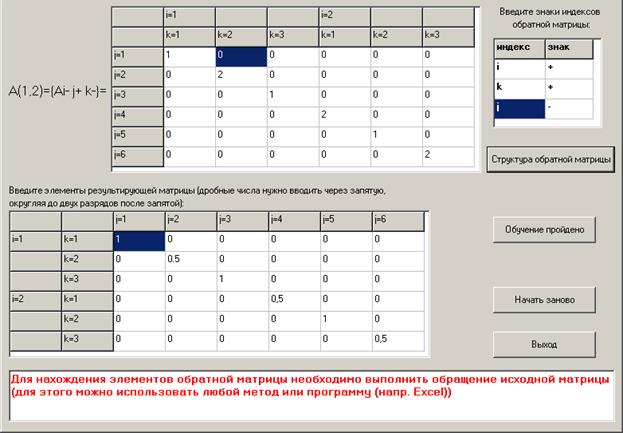
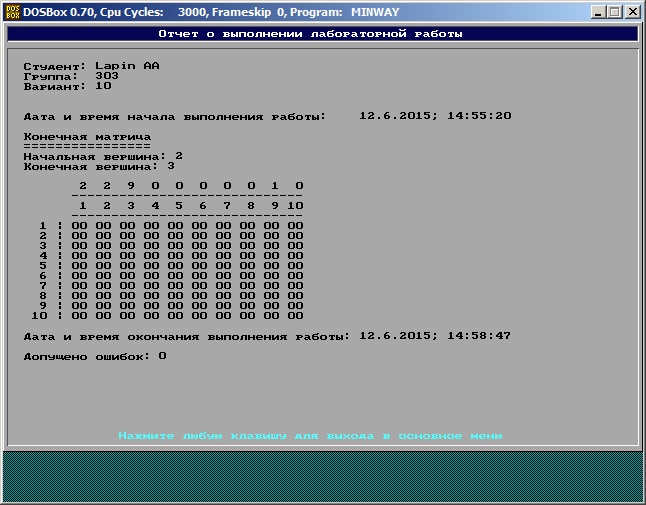
Результаты программного контроля исполнения работы
Лабораторная работа № 2
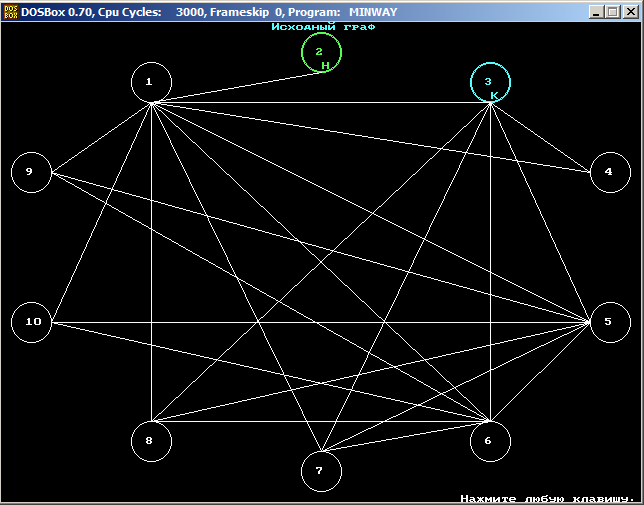
Экстремальный путь в графе.
Определение малейшего пути между двумя
Вершинами графа
Теоретическая часть
Разглядим метод ответа для случая многомерного графа. В конечном многомерном графе каждой дуге поставлено в соответствие число Сi1,i2,,,il,m1,m2,,ml, именуемое длиной дуги из вершины xi1,i2,,il в вершину xm1,m2,,ml. Требуется отыскать путь мельчайшей длины, ведущий из некоей вершины S в некую вершину t. Для применения табличного представления многомерных матриц введем помечивание индексов Ci1 ,i1 ,,m1 ,ml . Метод включает в себя 3 шага.
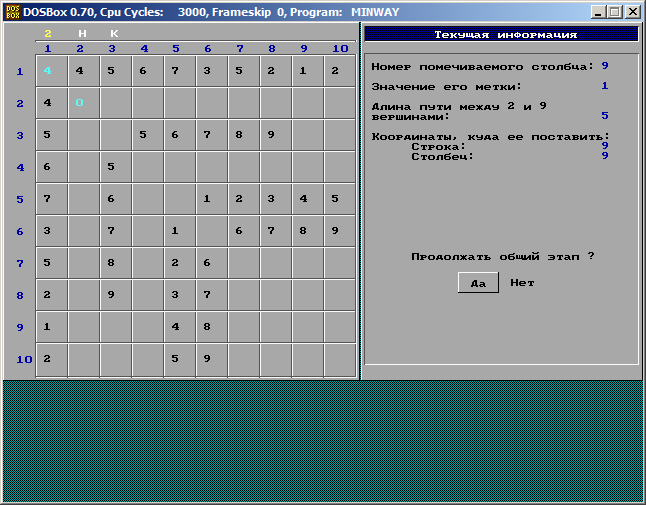
Предварительный ход. В табличном представлении матрицы C столбец помечивается знаком *. Диагональному элементу в столбце , т.е. , придается значение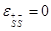 
. Помеченные вершины будем относить к множеству R, непомеченные – к , т.е. S I R.
Неспециализированный ход. Разглядим все дуги, исходящие из множества помеченных вершин R и заканчивающиеся на непомеченных вершинах . Для каждой дуги отыщем
hm ,l =Cm ,m + Cm ,l ,
для чего входим в -строчок и складываем элемент и диагональный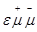 
элемент строки 
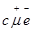. Находим минимум , после этого столбец l i помечаем значением мультииндекса , а диагональному элементу столбца l i придаем значение = 
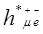. И без того до тех пор, пока не пометим вершину t.
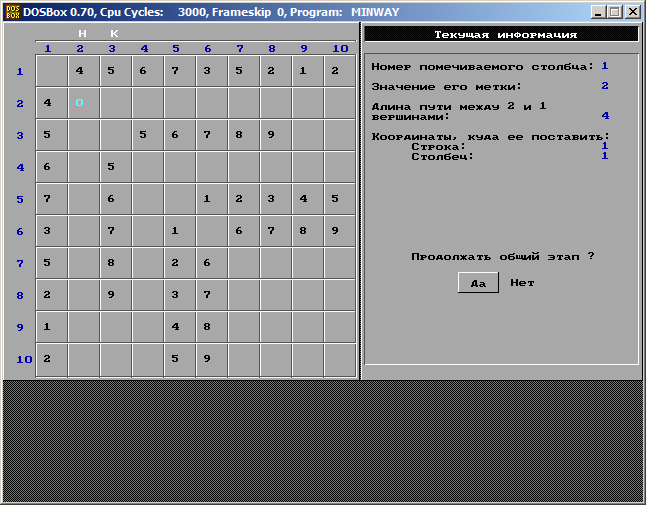
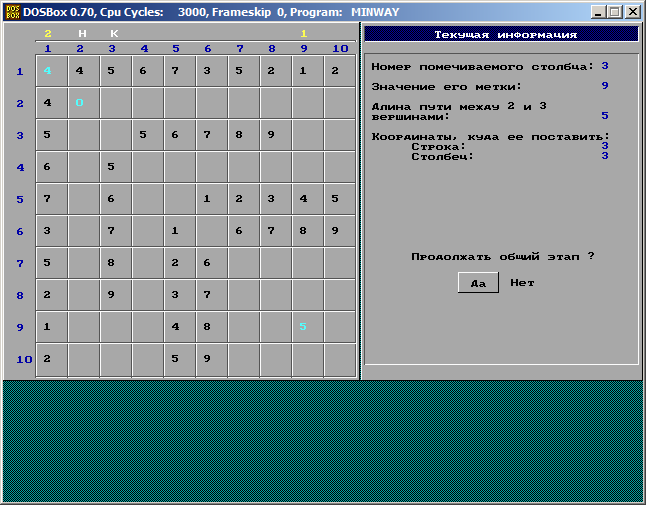
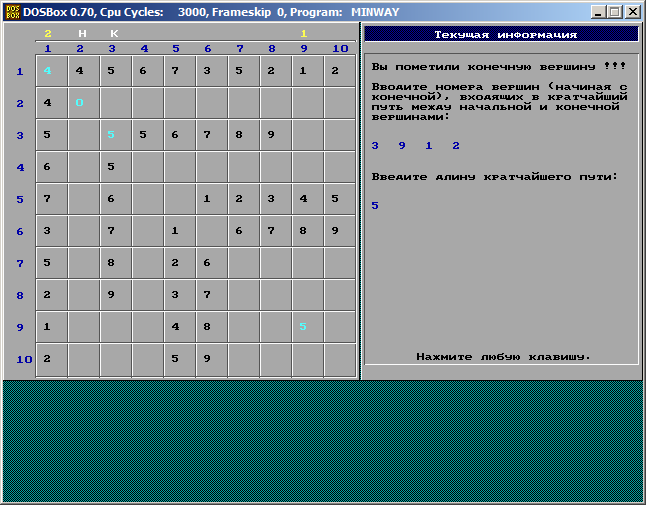
Последний ход. Искомый путь определяем, двигаясь от t к S по отметкам вершин.
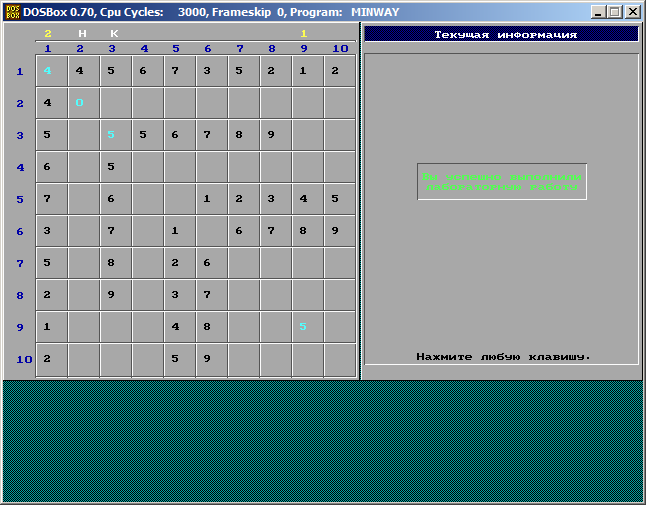
Программа даёт возможность студенту пройти режим обучения, после этого проверить собственные знания в режиме контроля. В обоих режимах возможно взглянуть структуру графа.
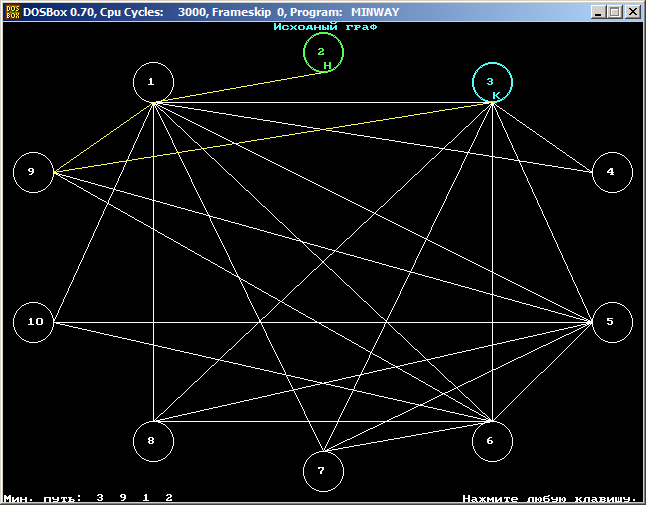
Лабораторная работа № 3
Малейший остов графа
Понятие дерева
Одним из самые важных понятий теории графов есть дерево. Его упрощенное определение возможно дать так. Дерево – граф, имеющий начало, от которого дуги (ребра) расходятся, как ветви дерева. Дерево, как и граф, возможно ориентированным и неориентированным.
Неориентированное дерево – это очень сильно связный граф, не имеющий циклов. Ориентированное дерево представляет собой ориентированный граф без циклов, в котором в каждую вершину должна быть направлена лишь одна дуга, не считая корневой вершины, куда не заходит ни одна дуга. Остовное дерево графа, либо остов графа, имеет то же самое множество вершин, что и исходный граф, но множество дуг (ребер) остовного дерева есть подмножеством множества дуг (ребер) исходного графа.