В случае, если дифференцируемая функция имеет локальный экстремум во внутренней (не нескончаемой) точке , то ее градиент в данной точке равен нулю.
Условие есть нужным, но не достаточны. Вероятны случаи, в то время, когда во внутренней точке градиент равен нулю, но у функции в том месте не будет ни минимума, ни максимума.
Пример.
.
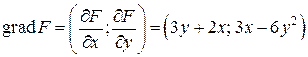 .
.
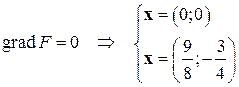
Так, в у функции возможно локальный максимум либо минимум лишь в двух точках. Более подробный анализ говорит о том, что первая точка не есть точкой экстремума. Вторая точка – точка локального минимума.
4. Методы определения условного экстремума
Пускай требуется решить задачу на отыскание условного экстремума:
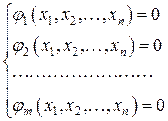 (1)
(1)
Существуют два подхода к ответу.
4.1. Выражение одной переменной через другие.
Возможно выразить из условий (1) кое-какие переменные через другие и подставить в функцию. Возьмём задачу на абсолютный экстремум.
Преимущества подхода:
O понижается число переменных;
O понижается число уравнений;
O подход интуитивно понятен.
Недочёты:
O навязывается неравнозначность переменных (главные и зависимые);
O по окончании исключения сложно проанализировать влияние условий;
O часто не удается очевидно выразить одну переменную через другие.
Последний недочёт оказывается критичным и непреодолимым при сложных зависимостях.
4.2. Способ множителей Лагранжа.
Для каждого ограничения вводится малоизвестный множитель . Затем ищется абсолютный экстремум для функции Лагранжа:
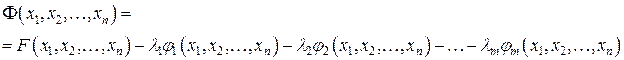
Другими словами записываются условий:
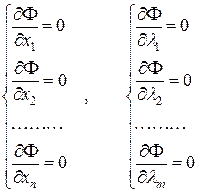
второй столбик условий, разумеется, есть совокупностью условий (1).
Недочёты подхода:
O подход интуитивно не очевидный;
O возрастает количество малоизвестных и количество уравнений;
O сложные зависимости остаются в совокупности.
Преимущества:
O постоянно удаётся записать всю совокупность уравнений перед тем, как приходится высказывать одну переменную через другие, следовательно, таковой подход универсален;
O множители Лагранжа имеют четкий суть и разрешают проанализировать влияние ограничений.
Суть множителей Лагранжа. Множитель Лагранжа, определенный для ограничения, показывает относительное изменение оптимального значения целевой функции при трансформации правой части ограничения. Другими словами, в случае, если правая часть какого-либо из ограничений (1) изменится на некое значение, то и оптимальное значение функции также изменится. Отношение трансформации функции к малому трансформации ограничения равняется множителю Лагранжа.
Также, множителя Лагранжа играют ключевую роль для задач нелинейного программирования, в то время, когда вместо ограничений равенствами (1) присутствуют ограничения соответствующими неравенствами ( вместо ). Тогда ненулевой множитель Лагранжа свидетельствует исполнение в оптимальном случае соответствующего ограничения как равенства и имеет такой же суть как для равенств. Нулевой множитель Лагранжа показывает, что в оптимальном случае соответствующее ограничение выполнено как строгое неравенство.
4.3. В качестве третьего подхода возможно советовать комбинировать оба метода. Выразить те переменные, каковые легко выражаются через другие. Подставить везде, тем самым, сократив число переменных и ограничений. Потом применять метод Лагранжа.
5. Теорема Куна-Таккера для задачи нелинейной оптимизации.
способ применения и Простейшая интерпретация
Теорема Куна-Таккера – главная теорема, дающая возможность решить аналитически задачи нелинейного программирования (оптимизации). Неспециализированная математическая формулировка теоремы достаточно сложна. Тут мы приведем ее упрощенный вариант, разрешающий решать конкретные задачи оптимизации, появляющиеся в управлении и экономике.
Для задачи нелинейного программирования:
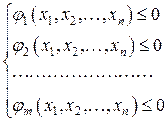 (2)
(2)
нужным для точки экстремума есть исполнение одного из условий:
1) равенство нулю градиента функции в данной точке;
2) отсутствие градиента функции в точке;
3) равенство нулю хотя бы одного из ограничений (2);
4) нескончаемая точка.
Увидим, что равенство нулю ограничений (2) достигается на границе области.
Тогда для отыскания наилучшего значения функции и переменных , при которых оно достигается нужно выполнить следующий метод поиска глобального экстремума:
1) отыскать градиент функции;
2) выяснить все точки, где градиент равен нулю; в тех из них, каковые удовлетворяют ограничениям, вычислить значение функции;
3) выяснить все точки, где градиент не существует; в тех из них, каковые удовлетворяют ограничениям, вычислить значение функции (в случае, если допустимо);
4) выяснить большие и минимальные значения функции на границах области;
5) изучить функцию на бесконечности, отыскать в том месте большое и минимальное значение функции;
6) из определенных значений функции во всех возможно вероятных местах экстремума выбрать самое громадное (при поиске максимума) либо самое мелкое (при поиске минимума); точка, в которой достигается это значение, будет ответом задачи оптимизации.
В общем случае выполнить эти операции весьма непросто. В п.п. 2) и 3) градиент предположительно составит нулю либо не существовать в нескончаемом количестве точек – к примеру на линии либо на поверхности в многомерном пространстве. Пункт 4) по большому счету ведет к независимой задаче поиска условного экстремума. Изучение функции на бесконечности – также непростая задача.
управления задач и Специфика экономики заметно упрощает использование этих операций.
Во-первых, в экономических постановках на бесконечности ни при каких обстоятельствах не бывает интересующего нас варианта. Бесконечность либо недостижима из-за ограничений, либо в том месте реализуется обратный случай. К примеру, возможно достигнуть нескончаемых убытков, но это не воображает интереса. Так, пункт 5) в задачах экономики в большинстве случаев не исследуется.
Во-вторых, точки, где градиент не существует, в детерминированных экономических постановках бывают известны заблаговременно. Такие точки, соответствующие разрывам и изломам функции, в любой момент должны иметь экономическое обоснование. Примером могут служить количество товара, при котором начинает функционировать скидка, величина дохода, в то время, когда изменяется ставка налогообложения и т.п. В отечественном примере про лесозаготовительный комбинат градиент не существует при количестве рабочих 70 (излом – начинает функционировать вторая величина затрат на человека) и 150 (разрыв – выплачивается субсидия).
В-третьих, применяемые для описания экономических обстановок функции достаточно несложны и имеют, в большинстве случаев, всего пара точек, где градиент равен нулю либо не имеют таких по большому счету.
Разбор примера задачи нелинейной оптимизации
Решим и проанализируем обрисованную выше обстановку принятия ответа для директора лесозаготовительного комбината.
Анализ будем проводить лишь с учетом переменных затрат. Как направляться из неспециализированной теории оптимизации, постоянное слагаемое не влияет на оптимальный замысел действий, изменяя лишь значение целевой функции.
Как видно из данных примера, целый анализ возможно провести в терминах количества рабочих. Обозначим через число рабочих на предприятии. Так как мы не можем выгнать с работы более 30 человек из имеющихся 70, то переменная ограничена снизу: .
Выпуск продукции пропорционален численности и равен м3 в мес. Доход от продажи в месяц тогда равен:
В случае, если вероятную субсидию при учесть в прибыльной части, то неспециализированную функцию месячного дохода возможно записать так:
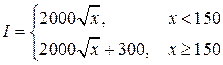 (3)
(3)
Если не нанимать новых сотрудников, то будет выполняться условие , а месячные затраты равны:
.
В случае, если нанять новых рабочих, то . Из этого количества рабочих 70 будут «ветхих», а – «новых». Тогда месячные затраты будут складываться из затрат на «ветхих» по 80 тыс. руб. на человека и затрат на новых по тыс. руб. на человека. Суммарные затраты составят:
.
В итоге неспециализированную функцию месячных затрат возможно записать в виде:
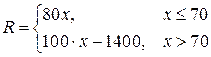 (4)
(4)
Прибыль комбината (не учитывая постоянных затрат) равна разнице между доходами (3) и переменными затратами (4) и запишется в виде:
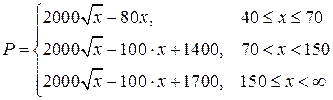 (5)
(5)
Так, математически задача формулируется так: отыскать , при котором функция прибыли (5) имеет максимум.
Разумеется, функция (5) изменяется непропорционально искомой переменной и задача есть нелинейной.
Пройдем для данной задачи все пункты метода поиска глобального экстремума.
1) Определим градиент функции. В этом случае функции одной переменной градиент сходится с производной. В случае, если функция задана различными выражениями на различных промежутках, то необходимо производные для каждого промежутка. Они будут честны при строгом исполнении ограничивающих промежутки неравенств:
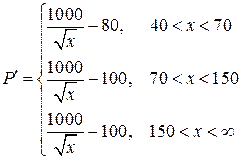 (6)
(6)
Как видно из выражения (6), производные на втором и третьем промежутках совпадают, но между ними при производная не существует, поскольку функция терпит разрыв.
2) Определим точки, где производная равна нулю. Для этого определим все , удовлетворяющие равенствам:
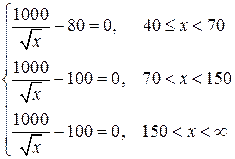
Разглядим промежуток . На нем имеем уравнение:
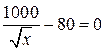 .
.
Решая уравнение, находим
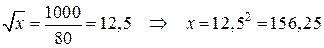 .
.
Но данное значение не попадает в промежуток: . Значит, на указанном промежутке нулей производной нет.
Разглядим промежуток . На нем имеем уравнение:
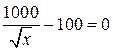 .
.
Решая уравнение, находим
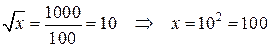 .
.
Данное значение в собственности разглядываемому промежутку: . Так, есть корнем производной.
Разглядим промежуток . На нем имеем уравнение:
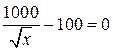 .
.
Решая уравнение, находим
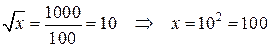 .
.
Это значение не в собственности разглядываемому промежутку: . Значит на указанном промежутке нулей производной нет.
Итак, производная равна нулю лишь в точке . Определим значение функции в данной точке:
.
Другими словами наняв 100 рабочих возьмём прибыль, равную 11400 тыс. руб.
3) Определим точки, где производная не существует. Это все точки границ промежутков. Отыщем в них значение функции:
.
В случае, если останутся прошлые 70 рабочих, то прибыль будет 11133 тыс. руб.
.
Наняв 150 рабочих возьмём прибыль, равную 11195 тыс. руб.
4) Единственной границей области в этом случае есть . Наряду с этим значении:
.
Другими словами при 40 работниках прибыль будет равна 9449 тыс. руб.
5) Поведение функции на бесконечности возможно не рассматривать, как в задачах экономики. Но, в случае, если это сделать, то возьмём:
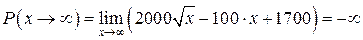 .
.
Как и ожидалось, нанимая неограниченное количество рабочих будем приобретать неограниченные убытки.
6) Из всех отысканных значений целевой функции выберем самое громадное. Собираем все значения совместно:
,
,
,
,
.
Как видно, громаднейшее значение достигается при .
Так, оптимальное управленческое решениебудет таким:
O Нужно привлечь к работе всего 100 человек: 70 уже имеющихся и 30 новых. В этом случае мы возьмём громаднейшую прибыль, равную 11 миллионов 400 тысяч рублей.
Ответить на вопросы, поставленные перед собой новым начальником, возможно так:
O Имеющееся количество рабочих не оптимально. Нужно нанять еще 30 человек. Нанимать рабочих до 150 человек не выгодно, поскольку приобретаемая субсидия вместе с ростом доходов не компенсирует полученный рост затрат.
Сделаем еще пара замечаний.
O В случае, если мы сравним суммы прибыли при текущем количестве рабочих (11 млн. 133 тыс. руб.) и оптимальным (11 млн. 400 тыс. руб.), то видно, что прибыль изменяется всего на 267 тыс. руб. либо менее чем на 3%. Нужно как направляться проанализировать, стоит ли поменять сложившийся вариант работы для таких малых трансформаций. Для анализа нужно уже будет учесть постоянные издержки. Если они громадны, то прибыль с их учетом делается намного меньше и дополнительные 267 тыс. руб. в месяц являются уже значительным выигрышем.
O Принятие на работу всего 150 человек приводит также к близкому денежному результату. Данный случай возможно рассмотрен как вариант расширения предприятия, в случае, если имеется возможность поиска лучшего варианта сбыта продукции.
Графическая интерпретация ответа.
Выстроим на одном графике все три функции, обрисовываемые уравнениями (4), (5), (6) (см рис. 1).
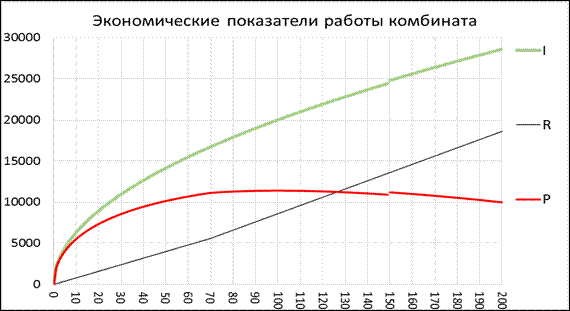
Рис. 1. Графики зависимости экономических показателей
от количества рабочих
Из графика видно, что оптимум прибыли достигается приблизительно при 100 рабочих.
График прибыли ведет себя достаточно медлено в окрестности большого значения, значит маленькие трансформации числа около рабочих 100 человек не очень сильно воздействуют на денежный итог.
специфика и Методика ответа задач
нелинейной оптимизации в MS Excel
Задачу оптимизации нелинейной функции (6) возможно было бы решить не методом анализа с применением производной, и применяя инструмент «Поиск ответа» в MS Excel.
В случае, если реализовать вычисления функции (6) по значению переменной в ячейке (см. рис. 2), то возможно выяснить оптимально значение переменной в данной ячейке.

Рис. 2. Реализация вычисления функции прибыли в MS Excel
Для оптимизации используем инструмент «Поиск ответа». Настраиваем параметры поиска ответа (рис. 3) следующим образом:
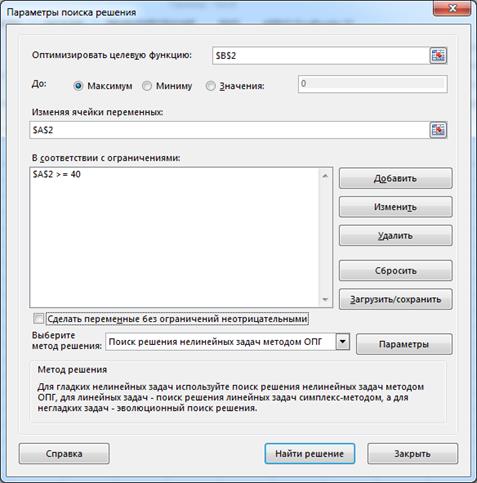
Рис. 3. Настройка инструмента «Поиск ответа»
- в поле «Оптимизировать целевую функцию» показываем ячейку, где реализована формула для прибыли;
- в поле «До» показываем «Максимум»;
- в поле «Изменяя ячейки переменных» показываем ячейку, предназначенную для значения переменной ;
- в поле «В соответствии с ограничениями» добавляем ограничение неосуществимости громадного увольнения ;
- состояние поля «Сделать переменные без ограничений неотрицательными» в отечественной задаче безразлично, поскольку единственная переменная ограничена;
- в поле «Выберите способ ответа» выбираем «Поиск ответа нелинейных задач способом ОПГ» (так как отечественная задача нелинейная).
Надавив кнопку «Отыскать ответ» приобретаем форму «Результаты поиска ответа» (рис. 4). Убедившись, что в этом окне написано «Ответ отыскано. Все условия и ограничения выполнены», выбираем «Сохранить отысканное ответ» и нажимаем кнопку «Ок».
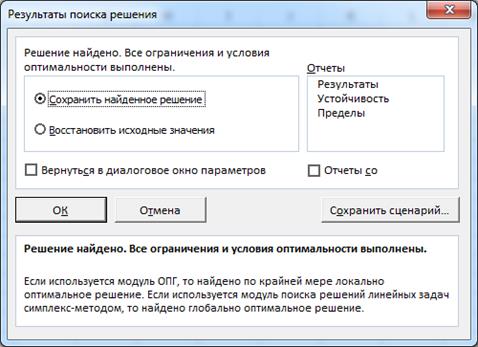
Рис. 4. Форма «Результаты поиска ответа»
В ячейке переменной приобретаем оптимальное ответ (рис. 5).

Рис. 5. Значения переменных по окончании оптимизации
Как видим, нам удалось отыскать верное ответ машинально.
Замечание: маленькое отличие значения в ячейке для искомой переменной от правильного (оказалось вместо ) обусловлено численной реализацией способа поиска. Это значение возможно смело округлить с заданной точностью.
Принципиально важно отметить такую специфику ответа нелинейных задач в MS Excel. Поиск ответа способом ОПГ ищет значения переменных от начального заданного, снабжая постоянное улучшение результата с текущего места. Такая реализация ведет к поиску локального, а не глобального экстремума. Так, «начав» поиск от 70 рабочих мы нашли оптимальное значение 100 человек. Начав же, к примеру, со 160 человек, возьмём «оптимальное» количество 150 (рис. 6). Выбрав же сначала 200 человек возможно опять прийти к оптимальному значению 100.

Рис. 6. Изменение ответа при смене начального приближения
Обрисованное свойство есть характерным для большинства методов численного поиска оптимумов в задачах нелинейной оптимизации. Для того, чтобы получить вправду глобальный максимум нужно попытаться выяснить оптимальное ответ для нескольких начальных приближений (в задачах экономики они, в большинстве случаев, выбираются легко из смысла задачи). В задачах с одной и двумя переменными сильно помогает построение графиков.
Задание для независимого ответа
Числовые условия задания формируются на базе двух последних цифр зачетной книжки либо студбилет. Исполнение чужого варианта задания не допускается.
В задании данной темы:
;
;
;
;
;
;
;
;
– последняя цифра номера зачетной книжки;
– предпоследняя цифра номера зачетной книжки.
Вы – новый начальник компании, создающей дорогостоящие автоматизированные станки. На данный момент компания создаёт 100 станков в год. Вам нужно проанализировать и при возможности оптимизировать работу компании.
Задание
Выясните оптимальное количество станков , которое нужно производить в год для оптимизации прибыли при следующих условиях функционирования компании:
- Цена продажи одного станка равна млн. руб.
- Постоянные издержки компании равны млн. руб., переменные издержки равны млн. руб.
- На отечественном рынке допустимо реализовать лишь станков в год. Все другая выпущенная продукция продается за рубежом за ту же цену, но с оплатой таможенной пошлины млн. руб. за любой импортируемый станок.
- Для большого выпуска продукции ( и более станков в год) нужно в текущем году заплатить экологическую пошлину, равную млн. руб.
O Сформулируйте оптимальное экономико-управленческое ответ в имеющихся условиях.
O Дайте экономическое обоснование взятого ответа.
O Приведите сравнение предлагаемого Вами замысла выпуска станков с применяемым ранее вариантом. Обоснуйте необходимость трансформаций.
O Приведите график зависимости прибыли от количества производимой продукции. Обоснуйте собственный ответ посредством графика.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Изучение операций в экономике : учеб. пособие / под ред. Н.Ш. Кремера – 2-е изд., перераб. и доп. – М. : Юрайт, 2010. – 430с.
2. Юкаева, В. С. Принятие управленческих ответов: учебник / В.С.Юкаева, Е.В.Зубарева, В.В.Чувикова – М.: Дашков и К, 2012. – 324с.
3. Дорогов, В. Г. Введение в алгоритмы и методы принятия ответов: Учебное пособие / В.Г.Дорогов, Я.О.Теплова. – М.: ИД ФОРУМ: ИНФРА-М, 2012. — 240 с. – режим доступа http://znanium.com.
4. Фатхутдинов, Р. А. Управленческие ответы: Учебник / Р.А. Фатхутдинов. ? М.: ИНФРА-М, 2010. ? 344 с. – режим доступа http://znanium.com.
5. Соколов, А. В. Способы оптимальных ответов. В 2 т. Т. 1. Неспециализированные положения. Математическое программирование: Учебное пособие / Соколов А.В., Токарев В.В. ? М.: ФИЗМАТЛИТ, 2011. – 564 с.
6. Токарев, В.В. Способы оптимальных ответов. В 2 т. Т.2. Многокритериальность. Динамика. Неопределенность.: Учебное пособие / Токарев В.В. – М.: ФИЗМАТЛИТ, 2011. – 420 с.
7. Арсеньев, Ю.Н. Принятие ответов. Интегрированные интеллектуальные совокупности : Учеб. пособ. / Ю.Н. Арсеньев, С. И. Шелобаев, Т. Ю. Давыдова. – М. : Издательство ЮНИТИ-ДАНА, 2003. – 270с.
8. Балдин, К.В. Управленческие ответы: Учебник / Балдин К.В., Воробьев С.Н., Уткин В.Б.. – М.: «Дашков и К°», 2012. — 496 с.
Электронные ресурсы:
9. Стандарт ФГОС ВПО
10. Иванов, Л. Н. Анализ стратегических ответов (эвристика) / Л.Н. Иванов. – М.: ИЦ РИОР: ИНФРА-М, 2010. – 177 с. – режим доступа http://znanium.com.
11. Дружелаускайте, Е. В. Мастерство верного принятия ответов / Е.В. Дружелаускайте. – М.: Форум, 2009. – 176 с. – режим доступа http://znanium.com.
12. Строева, Е. В. Разработка управленческих ответов: Учебное пособие / Е.В. Строева, Е.В. Лаврова. – М.: НИЦ Инфра-М, 2013. – 128 с. – режим доступа http://znanium.com.
13. Маркова, В. Д. Стратегический менеджмент: понятия, концепции, инструменты принятия ответов: Справочное пособие / В.Д. Маркова, С.А. Кузнецова. — М.: ИНФРА-М, 2012. — 320 с. – режим доступа http://znanium.com.
14. Бражко, Е. И. Управленческие ответы: Учебное пособие / Е.И. Бражко, Г.В. Серебрякова, Э.А. Смирнов. – М.: РИОР, 2008. — 126 с. – режим доступа http://znanium.com.
15. Ломакин, А. Л. Управленческие ответы: учебное пособие / А.Л. Ломакин, В.П. Буров, В.А. Морошкин. – М.: Форум, 2009. — 176 с. – режим доступа http://znanium.com.
16. Смирнов ,Э. А. Управленческие ответы: Учебник для институтов / Э.А. Смирнов. – М.: ИЦ РИОР, 2009. – 362 с. – режим доступа http://znanium.com.
17. Сайт материалов кафедры высшей математики ИЭУП (Казань) http://www.ieml-math.narod.ru
18. Электронные книжки совокупности дистанционного обучения Петербургский национальный исследовательский университет IT, оптики и механики http://de.ifmo.ru/bk_netra/select.php
19. Управление экономическими совокупностями. Электронный научный издание http://www.uecs.ru/
20. Официальные обучающие материалы Микрософт по Excel и вторым офисным программам http://office.Микрософт.com/ru-ru/excel-help
21. Задачи оптимизации в MS Excel http://exsolver.narod.ru/
22. Ответ прикладных задач в MS Excel http://citforum.ru/pp/excel70.shtml