Понятие нечеткой и лингвистической переменных употребляется при описании объектов и явлений посредством нечетких множеств.
Определение 5.15
Нечеткая переменная характеризуется тройкой , где ? — наименование переменной, X — универсальное множество (область определения ?), A — нечеткое множество на X, с функцией принадлежности µ A(x), обрисовывающей вероятные значения, каковые принимает нечёткая переменная ?. Как пример нечёткой переменой ? возможно привести нечёткое множество А «Средняя скорость автомобиля». В этом случае соответствующая нечёткая переменная возможно представлена следующим образом: , где А – нечёткое множество с функцией принадлежности в виде ТНИ Ат=.
Определение 5.16
Нечёткой лингвистической переменной именуется комплект , где
? — наименование лингвистической переменной;
Т — множество ее значений (терм-множество), воображающих собой наименования нечетких переменных, областью определения каждой из которых есть множество X. Множество T именуется базисным терм-множеством лингвистической переменной;
Х- универсальное множество – область определения нечётких переменных, каковые входят в определение лингвистической переменной ?;
G — синтаксическая процедура, которая обрисовывает процесс образования их новых и множества значений (термов) для данной лингвистической переменной, к примеру при помощи логических операций «и», «либо», «не», модификаторов типа «весьма», «легко» и т.д.
М — семантическая процедура, разрешающая перевоплотить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. организовать соответствующее нечеткое множество.
Пример 5.8
Пускай специалист определяет толщину производимого изделия посредством понятий «малая толщина», «средняя и» большая «толщина », наряду с этим минимальная толщина равна 10 мм, а большая — 80 мм.
Формализация для того чтобы описания возможно совершена посредством следующей лингвистической переменной , где
? — толщина изделия;
T — {«малая толщина», «средняя толщина», «громадная толщина»};
X — [10, 80];
G — процедура образования новых термов посредством связок «и», «либо» и модификаторов типа «весьма», «не», «легко» и др. К примеру: «малая либо средняя толщина», «малая толщина» и др.;
М — процедура задания на X = [10, 80] нечетких множеств А1= «малая толщина», А2 = «средняя толщина», А3= «громадная толщина» (рис.5.1), и нечетких множеств для термов из G в соответствии с правилами трансляции нечетких логических операций «и», «либо», «не», и операции возведения в степень, в частности растяжения и операции концентрации «весьма», «легко» и др. операции над нечеткими множествами вида: А1 А2, А2 , А2 , А0,5 и др.
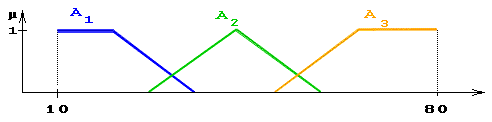
Рис. 5.1 Функции принадлежности нечетких множеств:
«малая толщина» = А1 , «средняя толщина»= А2, «громадная толщина»= А3.
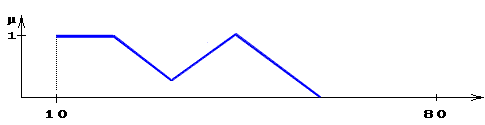
Рис. 5.2 Функция принадлежности:
нечеткое множество «малая либо средняя толщина» = А1EА2.
Замечание. Наровне с рассмотренными выше базисными значениями лингвистической переменной «толщина» (Т={«малая толщина», «средняя толщина», «громадная толщина»}) вероятны значения, зависящие от области определения Х. К примеру значения лингвистической переменной «толщина изделия» смогут быть выяснены как «около 20 мм», «около 50 мм», «около 70 мм», «в пределах от 55 до 60 мм» т.е. в виде нечетких интервалов и чисел.
Определение 5.17
Нечётким лингвистическим высказыванием будем именовать нечёткие высказывания следующих видов:
1. Высказывание «? имеется ?», где ? – наименование лингвистической переменной, ? – её значение, которому соответствует отдельный лингвистический терм из базисного терм-множества Т лингвистической переменной ?.
2. Высказывание «? имеется ?», где — модификатор, соответствующий таким словам, как «весьма», «более либо более», «довольно много больше» и вторым, каковые смогут быть взяты с применением процедур G и M данной лингвистической переменной.
3. Составные высказывания, образованные из высказываний видов 1 и 2 и нечётких логических операций конъюнкция, дизъюнкция, отрицание, импликация.
Пример 5.9
Нечёткое лингвистическое высказывание первого вида — «скорость автомобиля высокая», где лингвистической переменной «скорость автомобиля» присваивается значение «высокая».
Нечёткое лингвистическое высказывание второго вида — «скорость автомобиля довольно высокая» свидетельствует, что лингвистической переменной «скорость автомобиля» присваивается значение «высокая» с модификатором «весьма».
Нечёткое лингвистическое высказывание третьего типа «скорость автомобиля высокая и расстояние до светофора близкое» свидетельствует, что первой лингвистической переменной «скорость автомобиля» присваивается значение «высокая», а второй лингвистической переменной «расстояние до светофора» присваивается значение «близкое». Эти нечёткие высказывания первого типа соединены логической операцией нечёткая конъюнкция.
УПРАЖНЕНИЯ
1. Задайте нечёткие лингвистические переменные:
a. «Скорость автомобиля»;
b. «Возраст человека»;
c. «Температура окружающей среды»;
d. «Размер заработной плата».
2. Придумайте пример нечёткой лингвистической переменной.
3. Приведите пример нечёткого лингвистического высказывания.
Контрольные вопросы
1. Как вы осознаёте суть словосочетаний «нечёткая лингвистическая переменная» и «нечёткое лингвистическое высказывание»?
2. Существуют ли аналоги нечётких лингвистических переменных и высказываний в хорошей логике?
Библиографический перечень
1. Леоненков А. Нечёткое моделирование в среде MATLAB и fuzzyTECH [Текст]/ А.Леоненков – СПб.:БХВ-Петербург, 2005.- 736 с.
2. Саати Т. Принятие ответов. Способ анализа иерархий. [Текст]/Саати Т. — М.: Радио и Сообщение, 1989. – 316 с.
3. Саати Т. Л. Принятие ответов при обратных связях и зависимостях: Аналитические сети. [Текст]/Саати Т. — М.: Издательство ЛКИ, 2008. — 360 с.
4. Ярушкина Н.Г. Базы теории нечетких и гибридных совокупностей : Учеб. пособие для институтов / Н. Г. Ярушкина. — Гриф УМО. — М. : статистика и Финансы, 2004.
5. Новак В., Перфильева И. Математические правила нечеткой логики = Mathematical Principles of Fuzzy Logic / В. Новак, И. Перфильева, И. Мочкорж ; пер. с англ. А.Н. Аверкина. — М. : ФИЗМАТЛИТ, 2006. — 347 c
6. Яхъяева Г.Э.нейронные сети и Нечёткие множества : учеб. пособие / Г. Э. Яхъяева. — М. : Интернет-Ун-т Информ. Разработок: Двучлен, 2006. — 315 с.
Интернет-ресурсы
1. Масалович А. Ответ задач с применением инструментов, основанных на нечеткой логике. [Электронный ресурс] : Режим доступа: (URL http://www.tora-centre.ru/papers.htm 26.04.2012).
2. Масалович А., Золотарёв В. Нечёткая логика и правильные знания. [Электронный ресурс] : Режим доступа: (URL http://семь дней.tora-centre.ru/papers.htm 26.04.2012).
3. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику. [Электронный ресурс] : Режим доступа: (URL http://matlab.exponenta.ru/fuzzylogic/book1/index.php 26.04.2012).
Глоссарий
Агрегирование условий базы правил — процедура определения степени истинности условий по каждому из правил совокупности нечёткого вывода.
Аккумулирование заключений нечётких правил — процедура нахождения функции принадлежности для каждой из выходных лингвистических переменных.
Активация подзаключений базы правил – процедура нахождения степени истинности каждого из подзаключений правил нечётких определения и продукций функции принадлежности всех подзаключений для каждого правила в базе нечётких правил.
Антирефлексивное нечёткое отношение- двоичное нечёткое отношение, заданное на множестве Х Х, удовлетворяющее условию:
Х Х функция принадлежности отношения µQ()=0.
Антисимметричное нечёткое отношение — двоичное нечёткое отношение, заданное на множестве Х Х, удовлетворяющее условию: Х Х, причём хi хj, выполняется равенство: min{µQ(), µQ()}=0.
База правил совокупности нечёткого вывода — конечное множество правил вида «В случае, если…, ТО…», согласованных довольно применяемых в них лингвистических переменных.
Двоичные нечёткие отношения – n-арное нечёткое отношение при n=2. Q – двоичное нечёткое отношение, в случае, если Q={¦x1 Х1, х2 Х2, µQ [0,1]}.
Ближайшее чёткое множество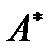 
довольно нечеткого множеству А, складывается из тех элементов универсума, для которых значения функции принадлежности µA(х) 0.5, а элементы, у которых, смогут µA(х) 0.5 принадлежать либо смогут не принадлежать множеству .
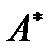Высота нечёткого множества Аэто числовая черта h нечёткого множества, которая находится по формуле: h=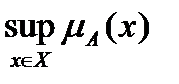 
.
Границы нечёткого множества А – это подмножество универсума Х,обозначаемоеGA , содержащее такие элементы универсума Х, для которых значения функции принадлежности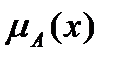 
хороши от 0 и 1,
т.е. GА={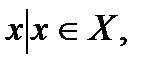 
0
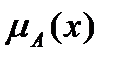
Дополнение нечёткого множества А это нечёткое множество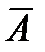 
, для всех элементов которого х 
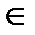Х выполняется условие: 
.
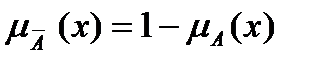Иерархия(иерархическая структура) — это графическое представление неприятности в виде перевернутого дерева, где любой элемент, за исключением самого верхнего, зависит от одного либо более элементов, расположенных выше разглядываемого эелемента.
Композиция нечётких двоичных взаимоотношений Q и R — это нечёткое отношение Q R, заданное на множестве X1´Х3 , функция принадлежности которого для X1´Х3 определяется формулой:
µQ R()= min{µQ(), µR()}}.
Множество ?-уровня нечеткого множества A именуется четкое подмножество универсального множества X, определяемое по формуле А? ={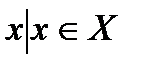 
|µA(х) ?} , где 
.
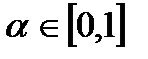Нечёткая величина — произвольное нечёткое множество А, заданное на множестве настоящих чисел R, т.е. нечёткое множество, для которого универсумом Х помогает всё множество R..
Нечёткая лингвистическая переменная именуется комплект , где, ? — наименование лингвистической переменной; Т — множество ее значений (терм-множество), воображающих собой наименования нечетких переменных, областью определения каждой из которых есть множество X; Х- универсальное множество – область определения нечётких переменных, каковые входят в определение лингвистической переменной ?;
G — синтаксическая процедура, которая обрисовывает процесс образования их множества T новых значений (термов) для данной лингвистической переменной, к примеру при помощи логических операций «и», «либо», «не», модификаторов типа «весьма», «легко» и т.д.;
М — семантическая процедура, разрешающая перевоплотить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. организовать соответствующее нечеткое множество. .
Нечёткая переменная – упорядоченная тройка элементов , где ? — наименование переменной, X — универсальное множество (область определения ?), A — нечеткое множество на X, с функцией принадлежности µ A(x), обрисовывающей вероятные значения, каковые принимает нечёткая переменная ?..
Нечёткое лингвистическое высказывание — нечёткое высказывание одного из следующих видов:
1. Высказывание «? имеется ?», где ? – наименование лингвистической переменной, ? – её значение, которому соответствует отдельный лингвистический терм из базисного терм-множества Т лингвистической переменной ?.
2. Высказывание «? имеется ?», где — модификатор, соответствующий таким словам, как «весьма», «более либо более», «довольно много больше» и вторым, каковые смогут быть взяты с применением процедур G и M данной лингвистической переменной.
3. Составные высказывания, образованные из высказываний видов 1 и 2 и нечётких логических операций конъюнкция, дизъюнкция, отрицание, импликация.
Нечёткая логическая формула определяется индуктивно следующим образом:
1. каждая нечёткая высказывательная переменная есть нечёткой логической формулой;
2. в случае, если F1 и F2 – нечёткие логические формулы, то ,F1 F2, F1 F2, F1 F2, F1-F2 – нечёткие логические формулы.
3. Вторых правил для образования нечётких логических формул не существует.
Нечёткий n-местныйпредикат Р(х1, х2, …, хn), заданный на множестве Х1 Х2 … Хn, это переменное высказывание, зависящее от нечётких переменных х1, х2,…,хn (x1 Х1, x1 Х1,…, xn Хn), которое преобразовывается в нечёткое высказывание, в случае, если всем переменным придать конкретные значения из соответствующих множеств.
Нечётко родные формулы – это нечёткие формулы, у которых степень равносильности на всех определённых комплектах значений переменных больше либо равна 0.5.
Нечётко подлинные формулы – это нечёткие формулы, каковые на всех определённых комплектах значений переменных принимают значение истинности больше либо равное 0.5.
Нечётко фальшивые формулы — это нечёткие формулы, каковые на всех определённых комплектах значений переменных принимают значение истинности меньше либо равное 0.5
Нечёткое высказывание — любое утверждение, о котором имеет суть делать выводы действительно оно либо ложно в той либо другой степени.
Нечеткое множество: пускай Х – универсальное множество, множество А – подмножество Х (A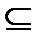 
Х). Нечетким множеством А именуется совокупность упорядоченных пар вида:, где х 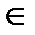Х, а µА(х) — функция принадлежности, которая ставит в соответствие каждому элементу х 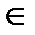Х некое настоящее число из отрезка[0,1]. Наряду с этим значение µА(х) =1 для некоего х 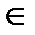Х свидетельствует, что элемент х определённо в собственности нечёткому множеству А, а значение µА(х) =0 свидетельствует, что элемент х определённо не в собственности нечёткому множеству А. Остальные значения функции µА(х) из промежутка (0,1) означают, что элемент х в собственности множеству А в той либо другой степени.
Нечёткое отношение: нечетким n-арным отношением именуется нечёткое множество Q, заданное на универсуме Х. Символически определение нечёткого отношения записывается в виде:
Q={¦x1 Х1, х2 Х2,…, хn Хn, µQ [0,1]}.
Носитель нечёткого множества A это простое подмножество As множества Х, которое содержит те и лишь те элементы Х, для которых значения функции принадлежности нечёткого множества А не равны 0, т.е. As={x| x 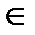Х, µА(х) 0}.
Объединение нечётких множеств А и В это нечёткое множество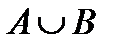 
, функция принадлежности которого имеет форму: 
.
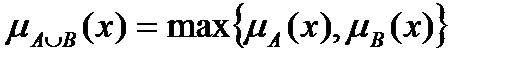(максминное объединение).
Относительное расстояние между нечёткими множествами находится по формулам:
относительное расстояние Хемминга:
r(A, B) = , r(A, B)I[0,1].
относительное Евклидово расстояние:
e(A, B)= 2 , e(A, B)I[0,1].
Пересечение нечётких множествА и В – это нечёткое множество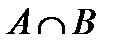 
, функция принадлежности которого имеет форму: 
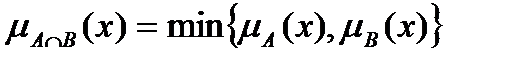(максминное пересечение).
Разность нечётких множеств А и В это нечёткое множество А\B, функция принадлежности которого имеет форму: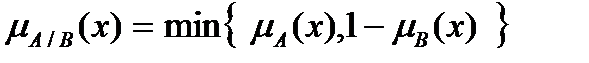 
.
Расстояние между нечёткими множествами А и В находится по формулам:
расстояние Хемминга (либо линейное расстояние):
?(A,В)=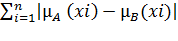 
, r(A, B)I[0, n].
Евклидово либо квадратичное расстояние:
e(A, B) = 2 , e(A, B)I[0, ].
Рефлексивное нечёткое отношение
Симметрическая разность нечётких множеств А и В это нечёткое множество А 
B, функция принадлежности которого имеет форму: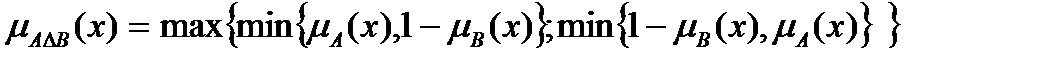 
.
Симметричное нечёткое отношение — двоичное нечёткое отношение Q, заданное на множестве Х Х, удовлетворяющее условию: Х Х выполняется равенство: µQ()= µQ().
Степень общности особенностей нечёткого предикатаР(х) для элементов множества Х именуется величина = (Р(х1)) (Р(х2)) (Р(хn)).
Степень равносильности нечётких формул F1(х1,х2,…,хn) и F2(х1,х2,…,хn) обозначается d(F1(х1,х2,…,хn); F2(х1,х2,…,хn)) и определяется выражением: (F1(х1,х2,…,хn);F2(х1,х2,…,хn))= (F1(х1,х2,…,хn) F2(х1,х2,…,хn)), где операция берётся по всем определённым комплектам степеней истинности высказывательных переменных.
Степень существования особенностей нечёткого предиката предиката Р(х) для элементов множества Х именуется величина = (Р(х1)) (Р(х2)) (Р(хn)).
Точки перехода нечёткого множестваА это множество ТА, складывающееся из элементов x 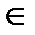Х , для которых 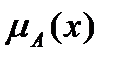=0.5 называютсяточками перехода нечёткого множества A, т.е. TA={x| x 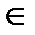Х, µА(х)=0.5}.
Транзитивное нечёткое отношение — двоичное нечёткое отношение Q , удовлетворяющее условию: хi, хj, хk Х имеет место равенство:
µQ() max хj Х {min{µQ(), µQ()}}=0.
Трапециевидная функция принадлежности —
Трапециевидный нечёткий промежуток
Треугольная функция принадлежности – это функция принадлежности нечёткого множества, которая задаётся алитическим выражением:
,
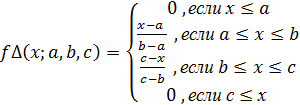где а, b, c – кое-какие числовые параметры, принимающие произвольные настоящие значения и упорядочены отношением: .
Треугольное нечёткое число(ТНЧ) это нечёткое число А?, функция принадлежности которого имеет треугольный вид . ТНЧ комфортно представить в виде упорядоченного множества А?=, где d – модальное значение ТНЧ, ? — левый коэффициент нечёткости и ? – правый коэффициент нечёткости: d=b, ?=b-a, ?=c-b.
Универсум – простое множество, другими словами множество, из элементов которого образованы все остальные множества.
Фаззификация входных переменных (введение нечёткости) — процедура нечёткого логического вывода, целью которой есть установление соответствия между конкретным (в большинстве случаев численным) значением хi из универсума Хi каждой входной лингвистической переменной ?i совокупности нечёткого вывода и значением функций принадлежности термов входной лингвистической переменной.
Функция принадлежности нечёткого множества А – это функция, которая каждому элементу х универсума Х ставит в соответствие число µА(х) из отрезка [0,1], которое показывает, в какой степени этот элемент х владеет особенностями нечёткого множества.
Ядро нечёткого множестваА — это простое множество А1, элементы которого удовлетворяют условию: А1 ={ 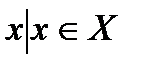|µA(х)=1}.
S-образная функция принадлежности либо сплайн-функция и в общем случае аналитически возможно задана следующим выражением:
,
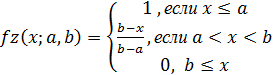где a и b – кое-какие числовые параметры, принимающие произвольные настоящие значения и упорядоченные отношением a .
S-образная функция принадлежности в общем случае возможно задана аналитически следующим выражением:
,
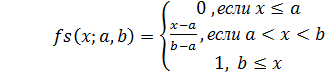где a и b – кое-какие числовые параметры, принимающие произвольные настоящие значения и упорядоченные отношением: a .
ОГЛАВЛЕНИЕ
Введение. 3
Тема 1. История приложений и развития теории.. 4
§ 1 История приложений и развития теории нечеткой математики 4
Тема 2. Нечёткие множества.. 13
§ 2.1 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ и ОПРЕДЕЛЕНИЕ НЕЧЁТКОГО МНОЖЕСТВА.. 14
§ 2.2 ВИДЫ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ.. 25
§2.3 Сравнение нечётких множеств, Операции над нечеткими множествами.. 29
§ 2.4 Расстояние между нечёткими множествами. Индексы нечёткости.. 37
Тема 3. Нечёткие размеры, числа и промежутки.. 42
§ 3.1 Определения нечёткой величины, нечёткого интервала и нечёткого числа.. 42
§3.2 Операции над ТНЧ и ТНИ.. 45
Тема 4. НЕЧЕТКИЕ ОТНОШЕНИЯ.. 50
4.1 Определение нечёткого отношения.. 51
§ 4.2 Композиция двух двоичных нечётких взаимоотношений.. 54
§ 4.3 Свойства двоичных нечётких взаимоотношений, заданных на одном универсуме. 58
Тема 5. элементы нечёткой логики.. 63
§5.1 логические операции и Нечёткие высказывания.. 64
§5.2 нечёткие логические их свойства и формулы.. 66
§ 5.3. кванторы и Нечёткие предикаты.. 71
§ 5.4 НЕЧЕТКАЯ И ЛИНГВИСТИЧЕСКАЯ ПЕРЕМЕННЫЕ. Нечёткие лингвистические высказывания.. 73
Библиографический перечень.. 77
Интернет-ресурсы.. 77
Глоссарий.. 78
ОГЛАВЛЕНИЕ. 86
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Елена Васильевна Бахусова
Тираж 100 экз.