Найдем определитель матрицы коэффициентов системы

Тема 6. Совокупности линейных алгебраических уравнений

Главные понятия СЛАУ

Совокупностью складывающейся из m линейных уравнений с n малоизвестными именуется совокупность вида

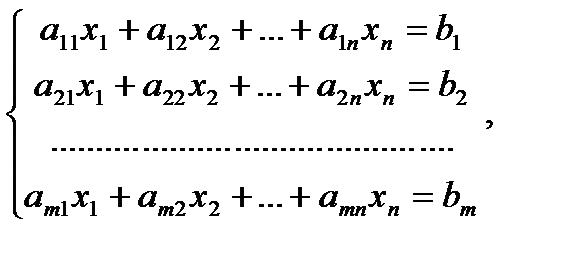(1)

где 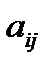, 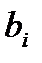— числа, 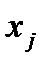— малоизвестные, n – число малоизвестных, m – число уравнений.

Ответом линейной совокупности (1) именуется упорядоченная совокупность чисел 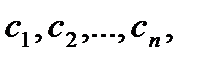каковые при подстановке вместо малоизвестных обращают каждое уравнение совокупности в верное равенство.

Линейная совокупность именуется неоднородной, в случае, если среди свободных участников имеются хорошие от нуля. В случае, если все свободные члены равны нулю, то линейная совокупность именуется однородной. Однородная совокупность имеет форму

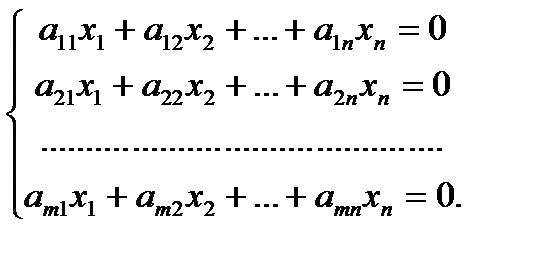(2)

Совокупность, имеющая хотя бы одно ответ, именуется совместной, а совокупность не имеющая ответов, — несовместной. Напомним, что однородная совокупность в любой момент совместна, поскольку она имеет нулевое ответ.

Совместная совокупность именуется определенной, если она имеет единственное ответ, и неизвестной, в случае, если имеет более одного решения.

Две совокупности именуются эквивалентными либо равносильными, в случае, если любое ответ одной из них есть так же ответом второй и обратно, т.е. в случае, если имеют одно да и то же множество ответов. Каждые две несовместные совокупности считаются эквивалентными.

Элементарными преобразованиями совокупности именуются следующие преобразования:

1) умножение уравнения совокупности на число, хорошее от нуля;

2) прибавление к одному уравнению совокупности другого ее уравнения, умноженного на любое число;

3) перестановка местами двух уравнений совокупности.

Определителем совокупности именуется определитель матрицы А из коэффициентов уравнений данной совокупности

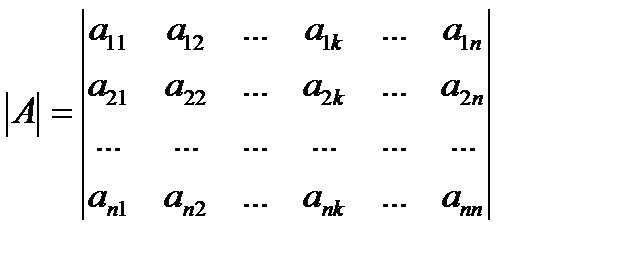
Матрица 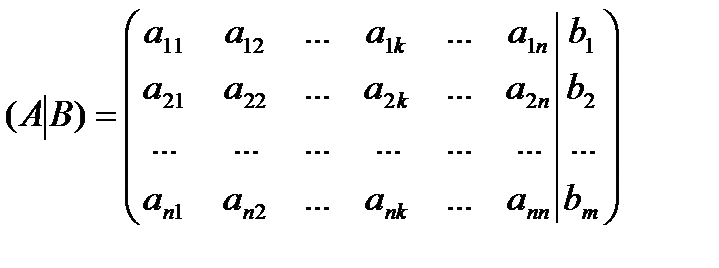полученная из главной присоединением столбца из свободных участников именуется расширенной матрицей совокупности.

Ответ СЛАУ по формулам Крамера

Пускай дана совокупность n линейных уравнений с n малоизвестными.

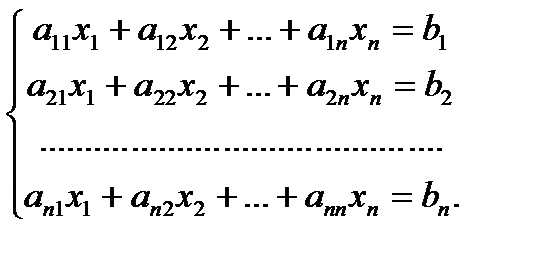
Обозначим через D определитель совокупности, а через Dk определитель, полученный заменой в определителе D столбца из коэффициентов при малоизвестной хk столбцом свободных участников совокупности, т.е.

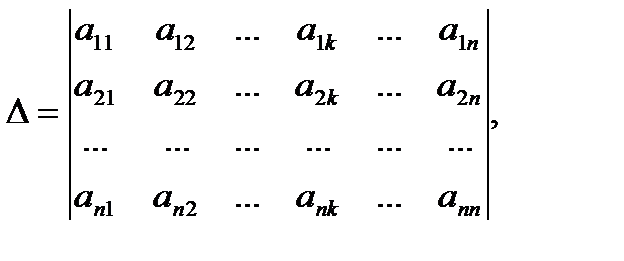
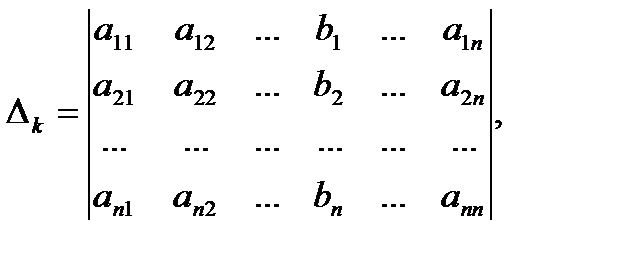
где k – одно из чисел 1, 2, …, n.

Теорема.

1) В случае, если 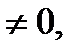совокупность (2.3) имеет единственное ответ, определяемое по формулам: .

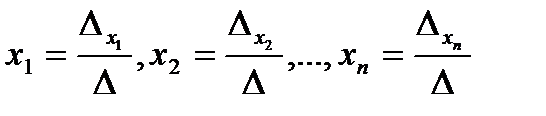2) В случае, если = =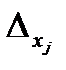0, совокупность имеет вечно довольно много ответов.

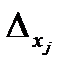
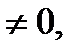3) В случае, если =0, а хотя бы один из совокупность не имеет ответов.

Пример. Решить совокупность линейных уравнений по формулам Крамера:

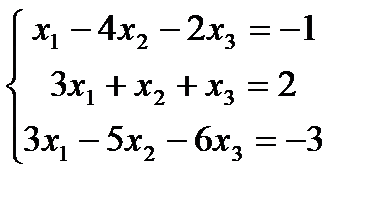
Ответ:

Отыщем определитель матрицы коэффициентов совокупности

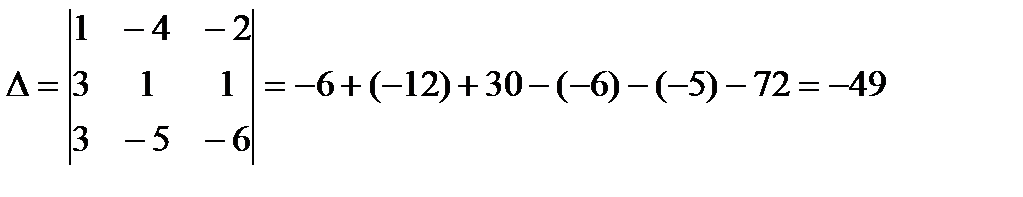
Так как ? # 0, то заданная совокупность уравнений имеет единственное ответ. Для этого вычислим определители ?j, получающиеся из определителя ? методом замены в нем столбца, складывающегося из коэффициентов при хj, столбцом свободных участников.

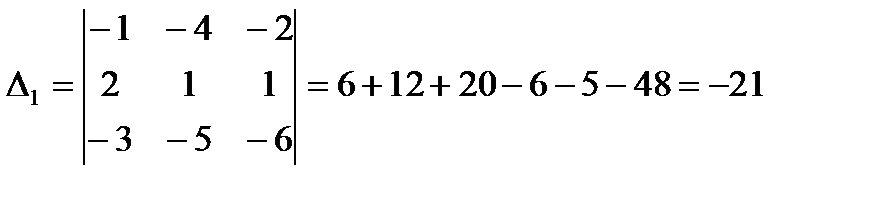
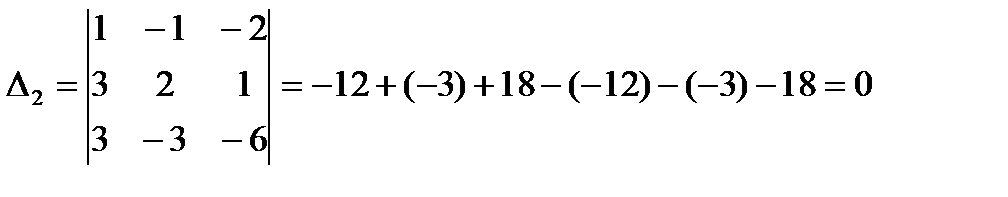
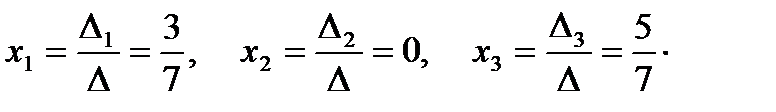
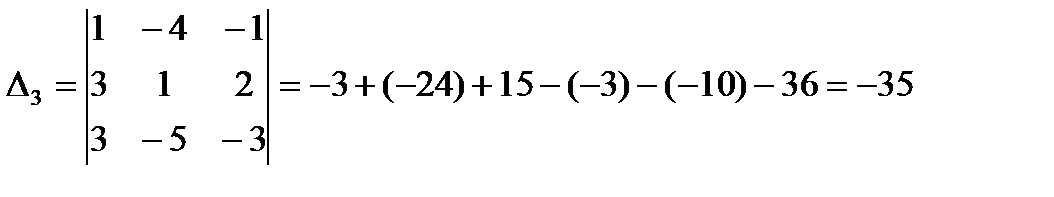
Из этого

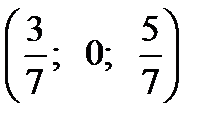
Ответ:

Примеры:

1. Разглядим совокупность 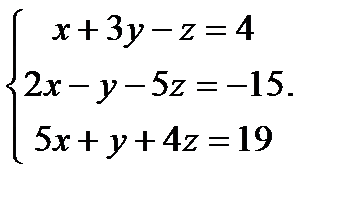, решенную в прошлом разделе способом Гаусса, и применим к ней правило Крамера. Отыщем все необходимые определители:

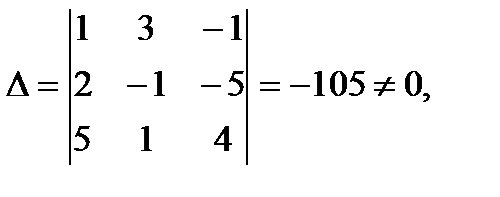следовательно, совокупность имеет единственное ответ.

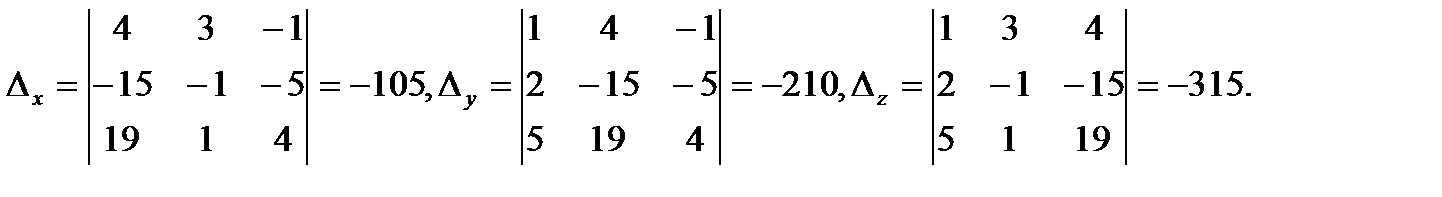
Из этого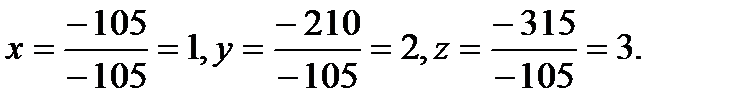

2. 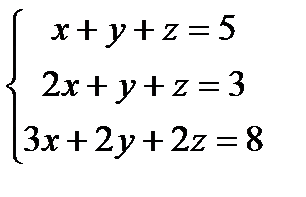. Тут 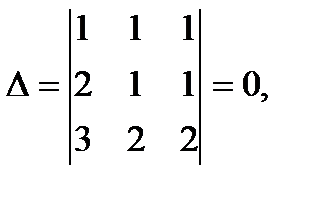потому, что имеет два однообразных столбца.

Следовательно, совокупность не имеет единственного ответа. Отыщем 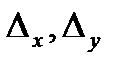и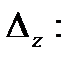

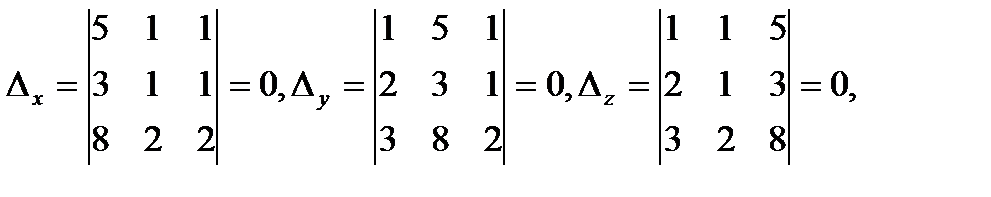исходя из этого совокупность имеет вечно довольно много ответов.

3. 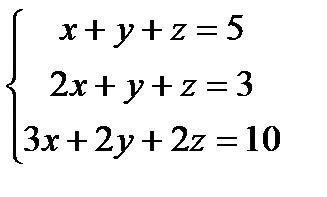. Для данной совокупности 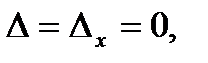но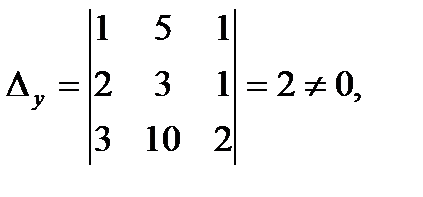

следовательно, ответов нет.

Система линейных уравнений. Метод обратной матрицы. Матричный метод.

Интересные записи:

• Нападающий удар. боковой и с переводом
• Написание контрольной работы
• Напишите с соблюдением всех необходимых реквизитов автобиографию (смотри образец в справочных материалах).
• Напишите с соблюдением всех необходимых реквизитов претензию о нарушении прав потребителя (смотри образец в справочных материалах).