Лекции
«Современная прикладная теория управления»
Модуль 1. Математические модели многомерных САУ
Тема 1.1. Математические модели САУ при наличии неопределенностей
Неприятности управления сложными совокупностями.
Совокупность представляется уравнением вида
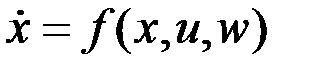 ,
,
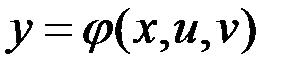 ,
,
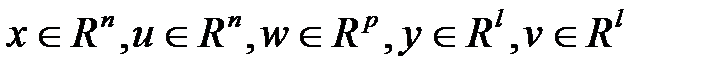 .
.
Сложными именуются совокупности, у которых имеются:
1. Много элементов систем, связанных между собой (N).
2. 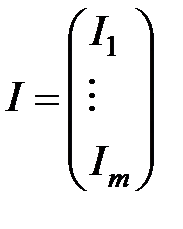 — векторный критерий качества. Довольно много требований по качеству.
— векторный критерий качества. Довольно много требований по качеству.
Возможно и без того: 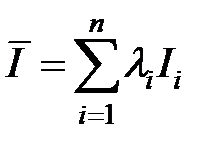
3. Влияние окружающей среды, которая заблаговременно возможно не известна.
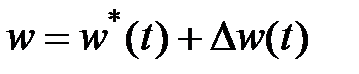 ,
, 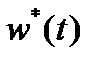 — известно,
— известно, 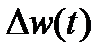 — неизвестно.
— неизвестно.
4. Нелинейность, нестационарность, неопределенность.
В природе чисто нестационарных (зависящих от t) совокупностей нет. Они получаются в следствии математических упрощений и преобразований:
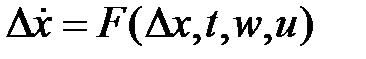 ,
,
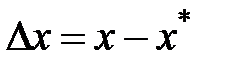 – отклонение от заданного режима
– отклонение от заданного режима 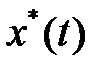 — вектора функции времени,
— вектора функции времени, 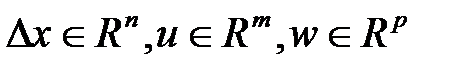 .
.
Подходы для ответа непростых динамических задач.
В большинстве случаев выполняют декомпозицию задачи, которая проводится по следующим направлениям изучения:
1. Функциональная декомпозиция – разбиение неспециализированной неприятности на пара частных задач разного уровня посредством математических моделей и декомпозиции задач, преобразованием этих задач с последующим упрощением.
2. Структурная декомпозиция – выделение более несложных систем, посредством расщепления совокупности на системы, а также за счет запасных управлений, каковые возможно разглядывать раздельно, не считая совокупностей согласованного управления, где должно выполняться условие согласованного перемещения.
К примеру, для совокупности
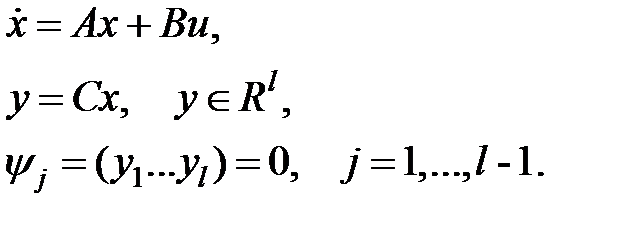
условием согласованного перемещения есть последнее уравнение.
3. Временная декомпозиция – выделение отдельных режимов работы совокупности , к примеру, в задачах динамики полета.
Математические модели динамических совокупностей
Для технических, производственных подвижных объектов, летательных аппаратов довольно часто применяют (либо смогут быть использованы) модели в виде нелинейных дифференциальных уравнений:
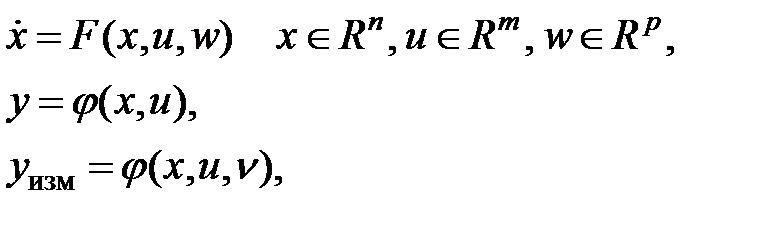 (1)
(1)
где

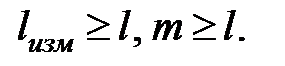
Тут правая часть уравнения 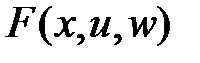 — вектор функция удовлетворяет единственности решения и условиям существования при
— вектор функция удовлетворяет единственности решения и условиям существования при 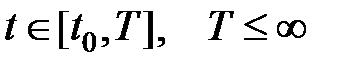 .
.
Пример 1.
 .
.
Для простоты до тех пор пока будем разглядывать случай y=yизм, 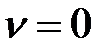 .
.
Разглядим пример построения нелинейной совокупности:
h – высота,
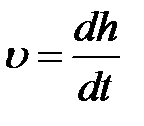 ,
, 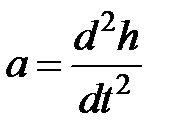
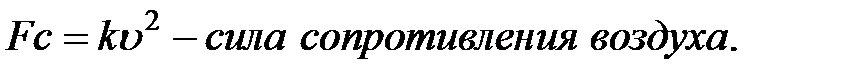
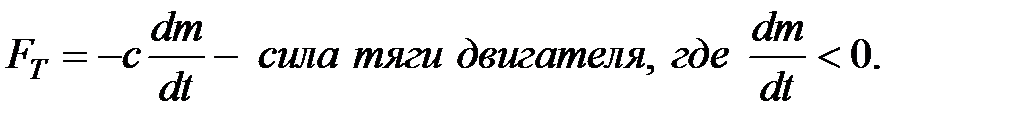
В соответствии с второму закону Ньютона
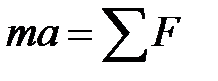
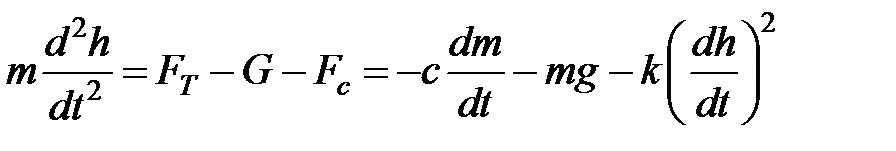
Введем обозначение:
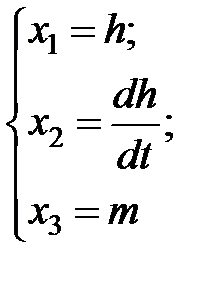
Преобразуем к следующему виду:
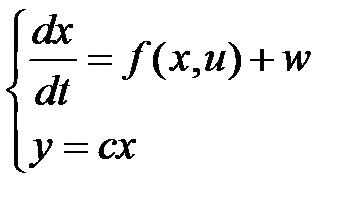
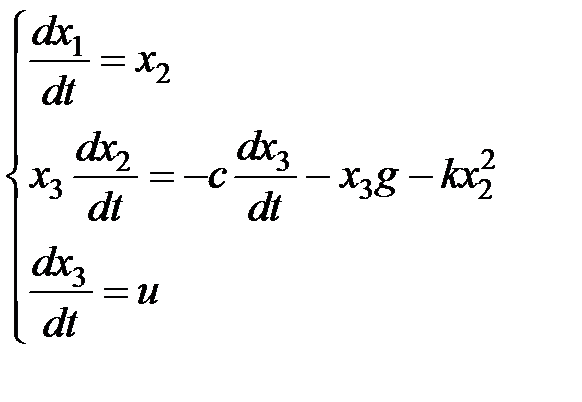 — вводим управление массой ракеты.
— вводим управление массой ракеты.
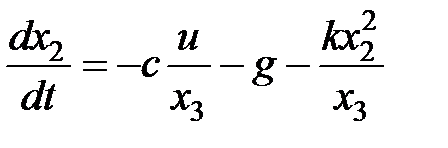
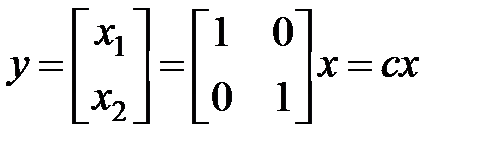
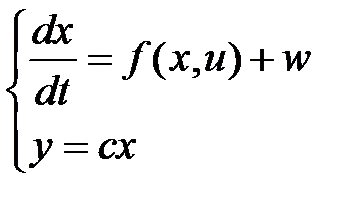
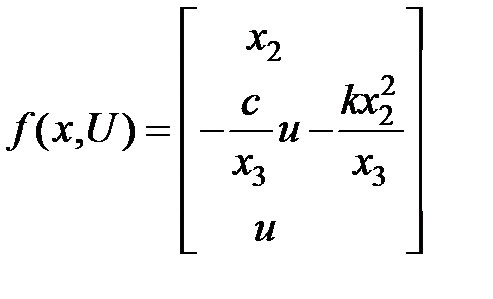 ,
, 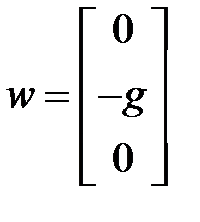 .
.
Линеаризованные модели для нелинейных совокупностей управления
Довольно часто удается применять упрощенные уравнения исходной совокупности в виде отклонений от некоего перемещения. Обоснованием этого есть возможность управления совокупностью так, дабы совокупность двигалась в окрестности данного перемещения.
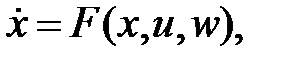 (1)
(1)
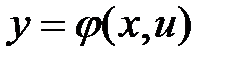 (2)
(2)
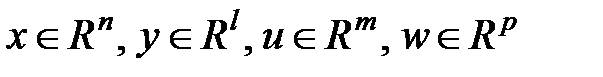 ,
,
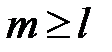 — число управлений больше числа выходов.
— число управлений больше числа выходов.
Довольно часто на практике совокупность трудится в некоей окрестности от заданного режима, что именуют номинальным либо невозмущенным. Частным случаем невозмущенного перемещения есть положение равновесия. В этом случае уравнение (1) возможно записать в отклонениях от номинального перемещения:
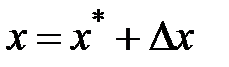 ,
, 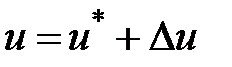 ,
, 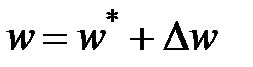 ,
,
где 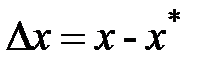 ,
, 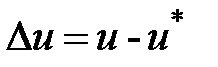 ,
, 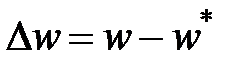 – отклонения от номинального перемещения.
– отклонения от номинального перемещения.
Будем считать, что 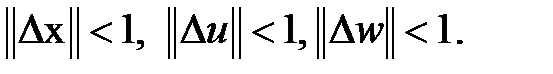
Разложим правую часть уравнения (1) в ряд Тейлора довольно номинального режима 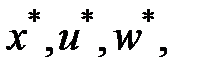 что удовлетворяет уравнению:
что удовлетворяет уравнению:
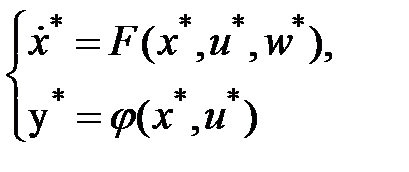
Уравнение (1) запишем в виде совокупности дифференциальных уравнений:
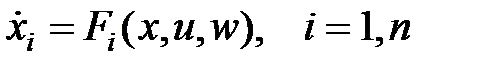 .
.
Тогда:
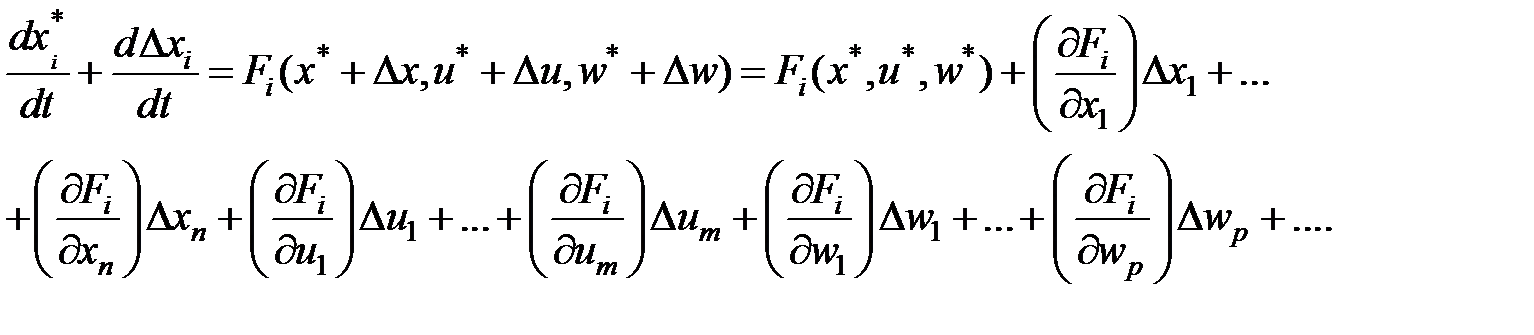
Учитывая, что
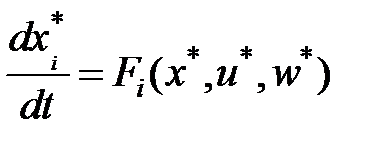 ,
,
и отбрасывая слагаемые малого порядка (произведения отклонений), возьмём
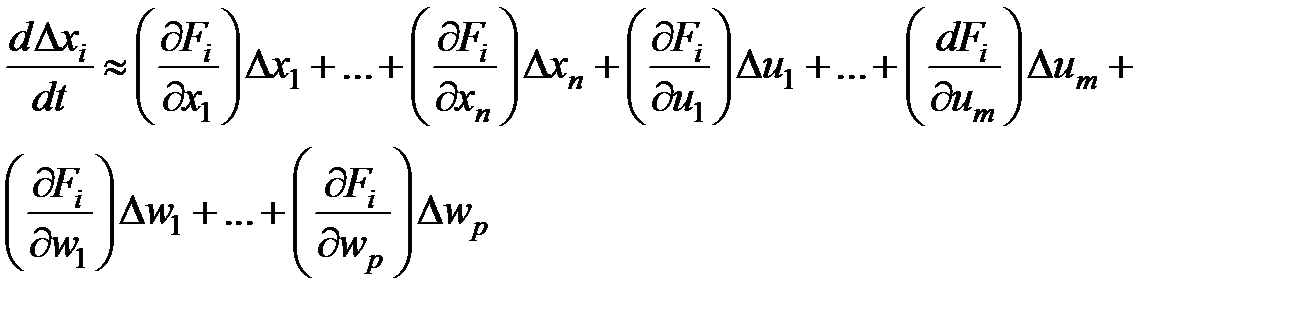
Запишем совокупность взятых уравнений в матричном виде:
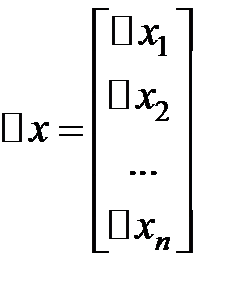 ,
, 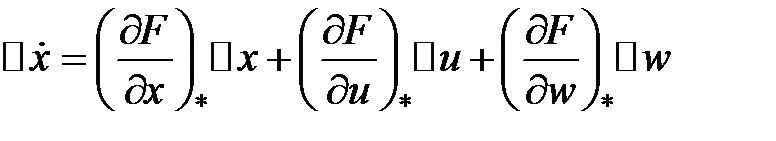 ,
,
где 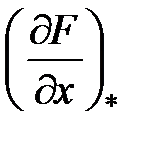 — матрица Якоби,
— матрица Якоби,
равная 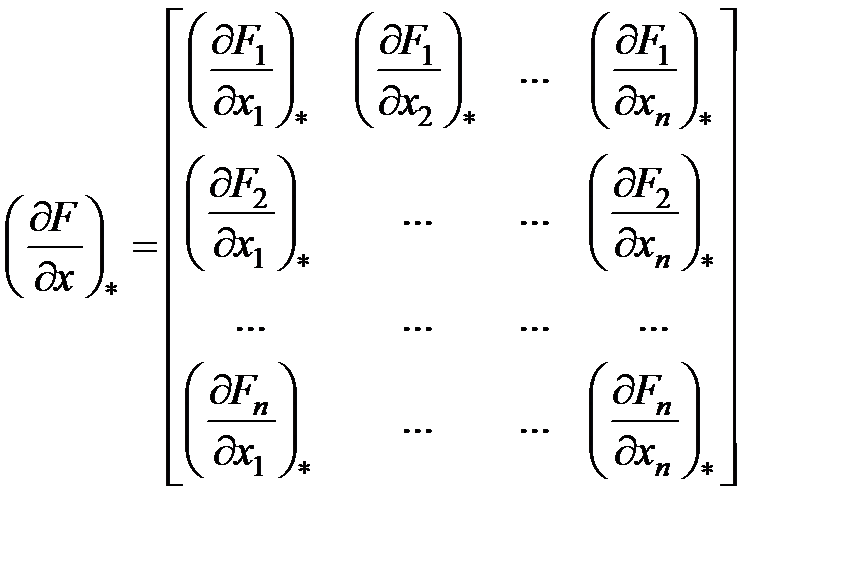
Символ * говорит о том, что необходимо подставить значение номинального перемещения: 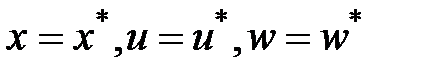 .
.
Подобно находим матрицу для координат и координат управления векторавозмущения:
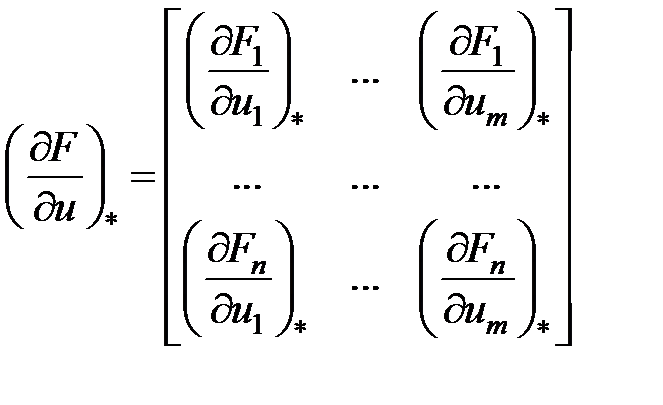 ,
, 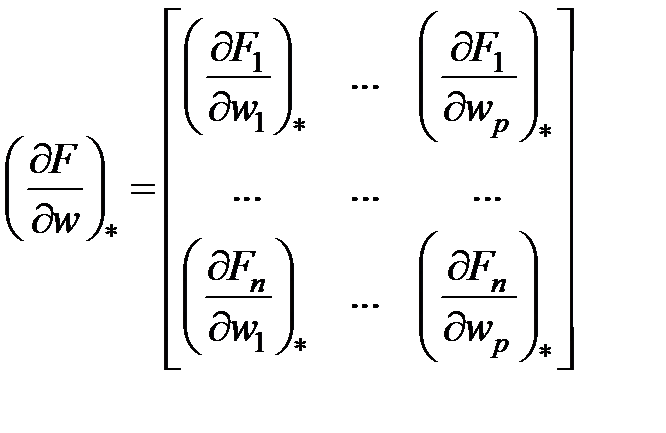 .
.
Подобно и для производных координат вектора 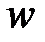 .
.
Выражение для 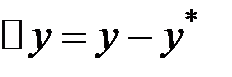 записывается подобно выражению
записывается подобно выражению 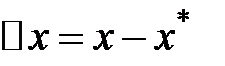 :
:
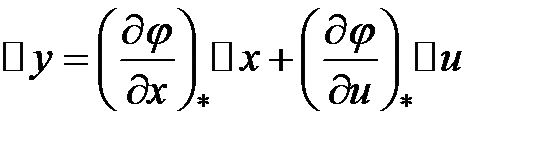
Так, возьмём уравнения в отклонениях от номинального режима:
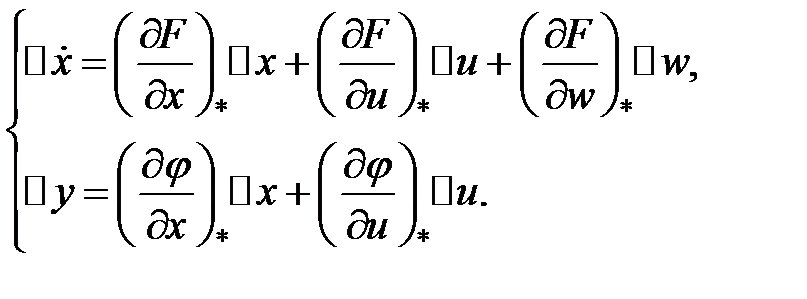
С учетом обозначений
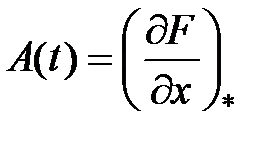
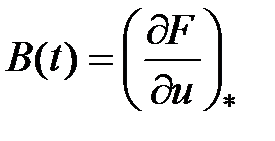
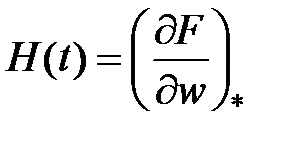
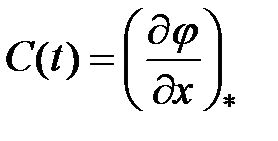
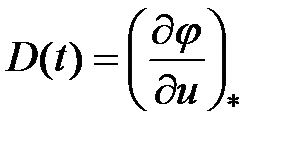
возьмём совокупность
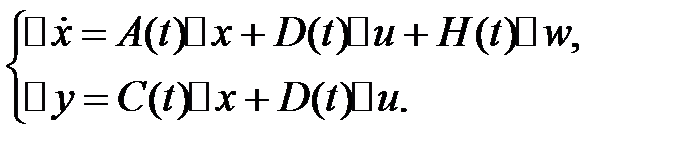
Потому, что 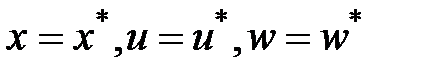 — функции времени, то и приобретаемые матрицы становятся функциями времени.
— функции времени, то и приобретаемые матрицы становятся функциями времени.
Пример 1.
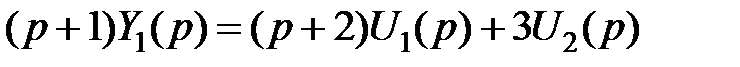 ,
,
Учитывая, что 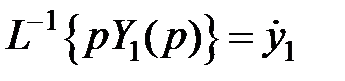 ,
, 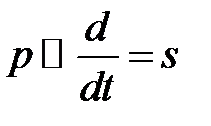 , возьмём:
, возьмём:
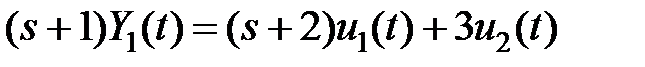 ,
,
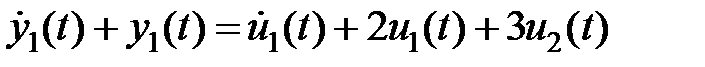 .
.
Пример 1.
Пускай задана исходная совокупность
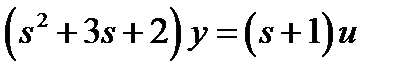
1) По схеме Горнера возьмём модель в пространстве состояний:
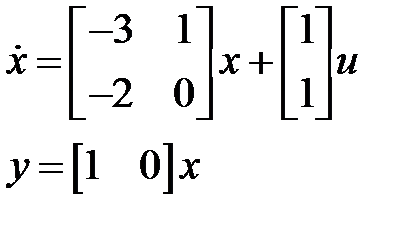
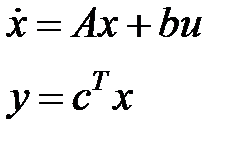
2) Посредством пакета MatLab возьмём:
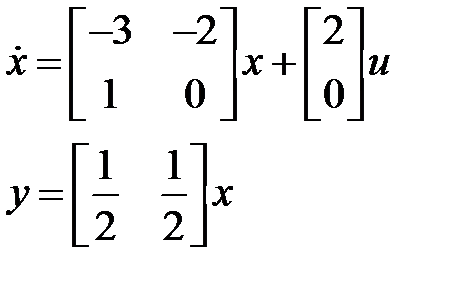
либо
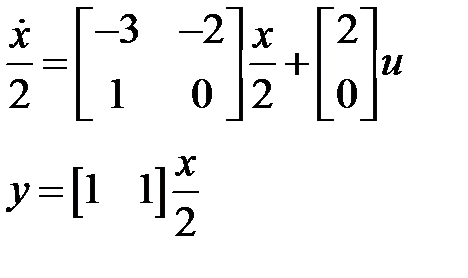
Возможно переписать в виде
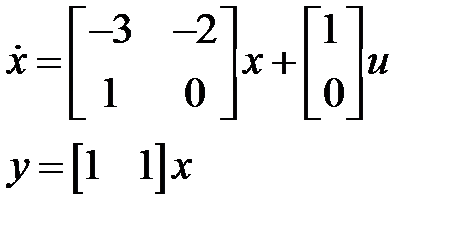 .
.
Так, взяли разные совокупности, каковые имеют одну передаточную функцию, но имеют различные особенности:
1) 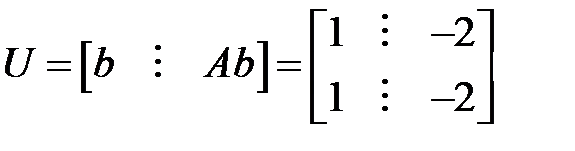 ,
, 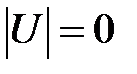 — неуправляема
— неуправляема
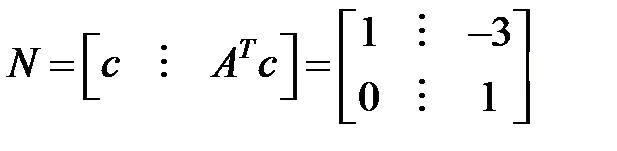 ,
, 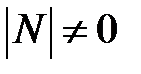 — замечаема
— замечаема
2) 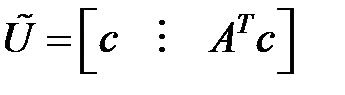 ,
, 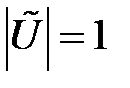 — управляема
— управляема
 ,
, 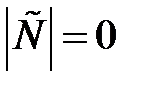 — ненаблюдаема
— ненаблюдаема
В конечном итоге верной есть модель 1).
Модели внешних действий
Разглядим управляемую совокупность:
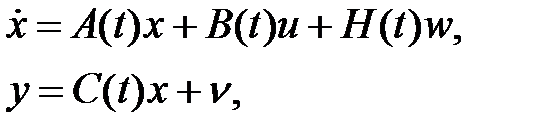
где 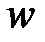 – возмущение,
– возмущение, 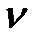 – помеха измерений.
– помеха измерений.
Внешние действия возможно поделить на регулярные и нерегулярные и случайные.
Регулярные действия – это такие действия, каковые возможно представить посредством ответа дифференциальных уравнений при заблаговременно малоизвестных начальных условиях.
Нерегулярные внешние действия – имеют ограниченную скорость трансформации и их возможно записать посредством неравенств, удовлетворяющих некоторым ограничениям.
Случайные действия – смогут иметь разрывы и их нельзя представить в виде модели в времени.
Разглядим регулярные и нерегулярные действия. Наряду с этим произвольное действие будем воображать в виде суммы регулярного и нерегулярного действия: 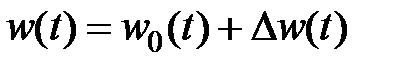 .
.
Случай стационарной совокупности
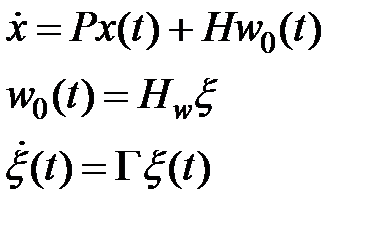
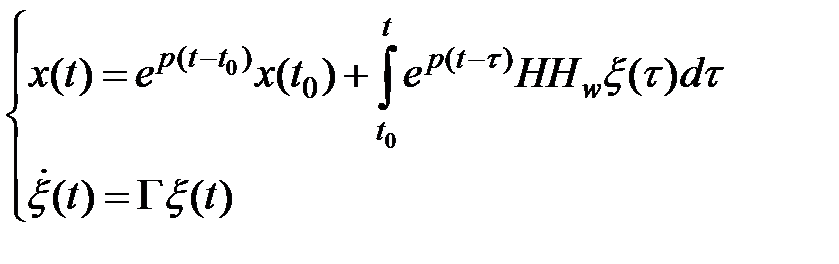
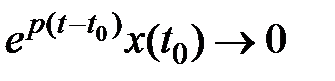 при
при 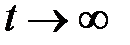 ,
, 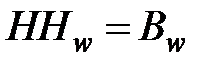
Нужно отыскать: 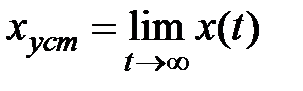
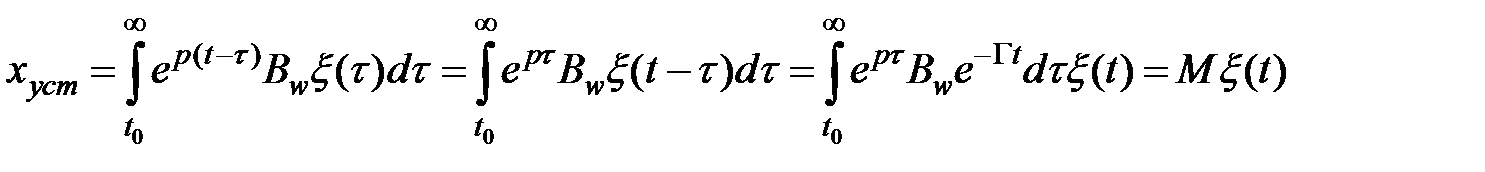
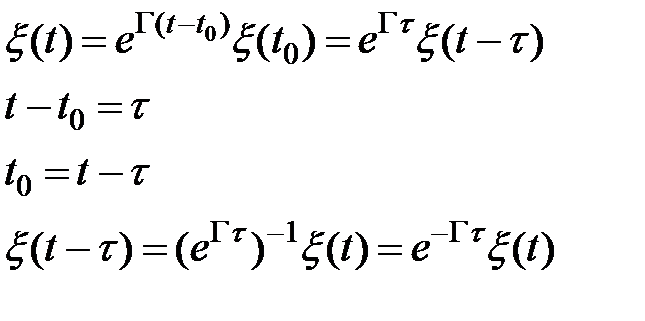
Разглядим случай, в то время, когда корни характеристических уравнений:
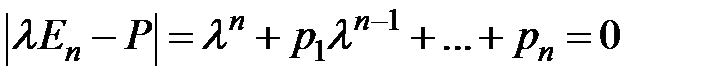
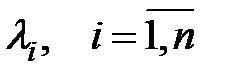 — разные
— разные
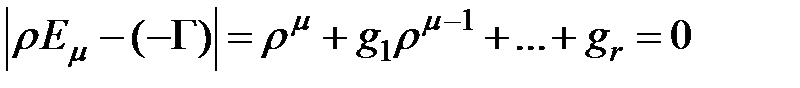
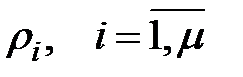 — разные
— разные
Тогда
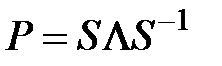 ,
,
где 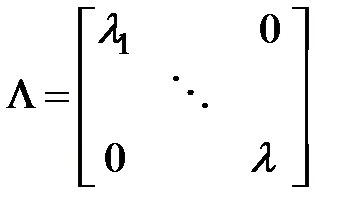 ,
,
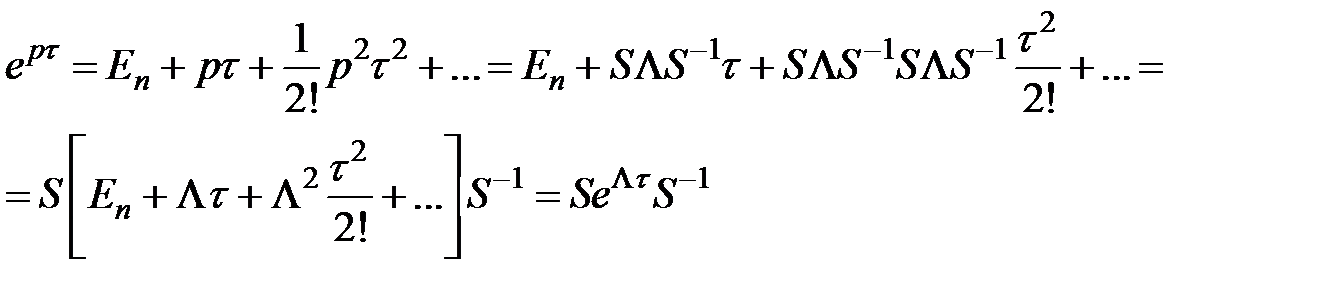
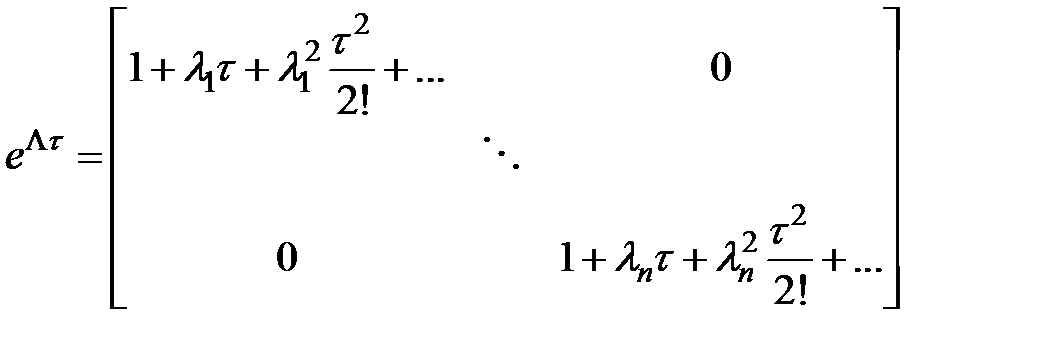
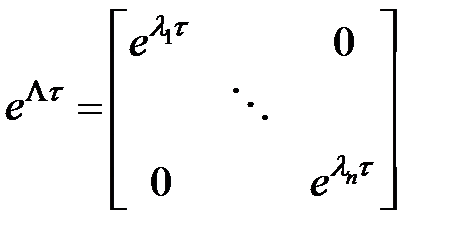
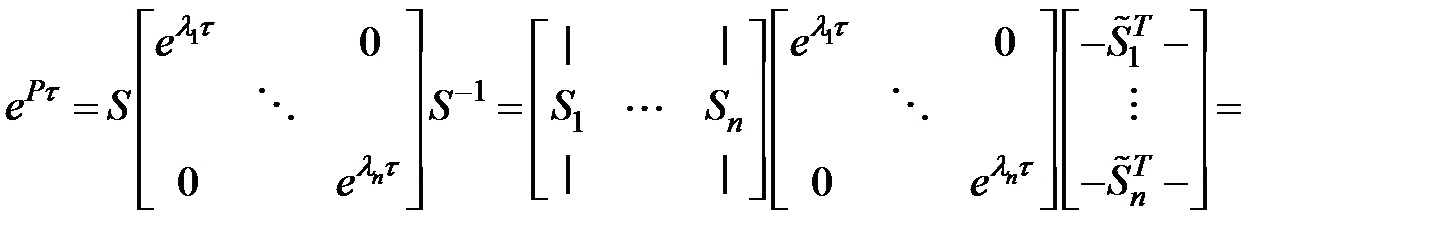
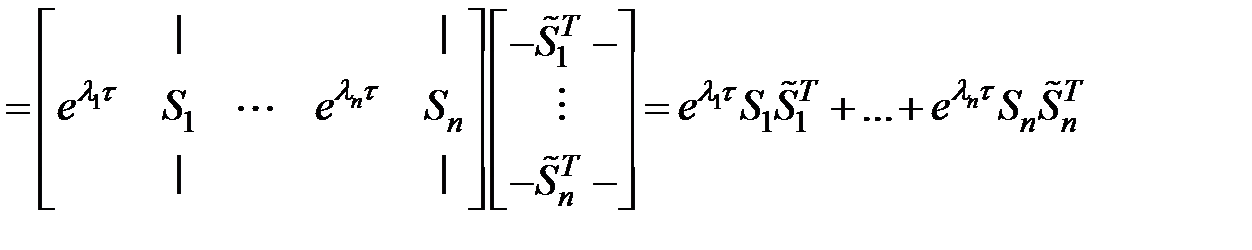
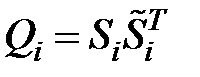 — личная матрица.
— личная матрица.
Тогда получается формула
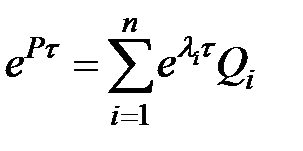
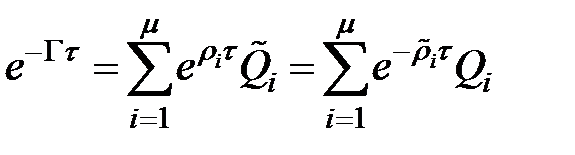
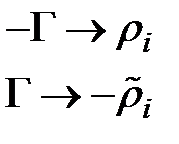
Тогда
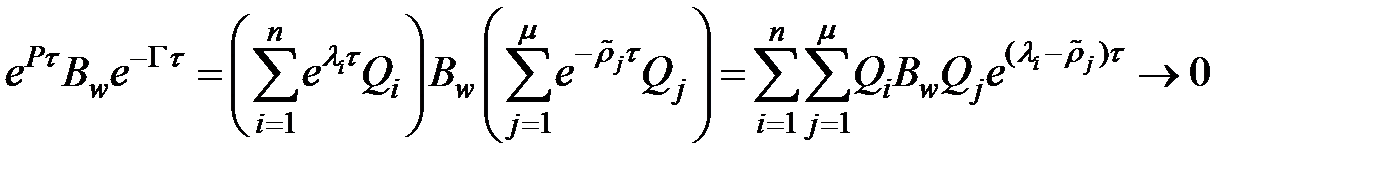 при
при 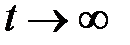
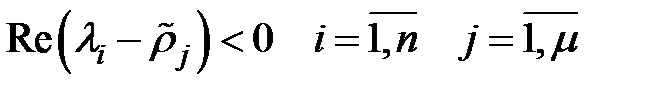
Такое будет при:
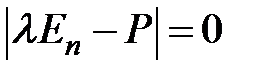
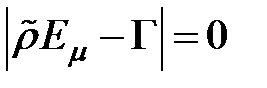
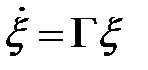
Достаточное условие сходимости:
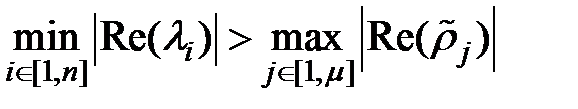
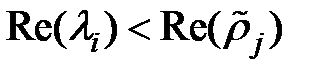
Подставим в исходное уравнение
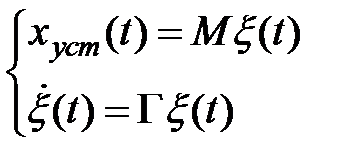 ,
,
возьмём
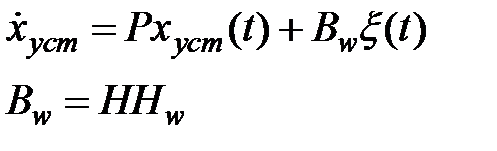
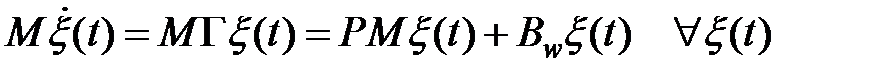
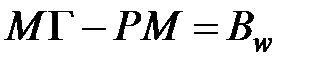
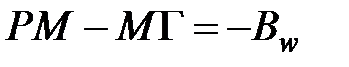 — уравнение Сильвестра (похоже на уравнение Ляпунова в случае, если
— уравнение Сильвестра (похоже на уравнение Ляпунова в случае, если 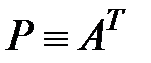 ,
, 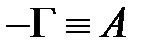 и
и 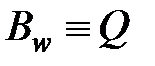 ).
).
Пример 1. Выяснить установившееся перемещение посредством уравнения Сильвестра.
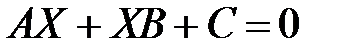 — уравнение в MatLab
— уравнение в MatLab
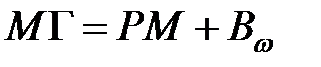
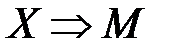
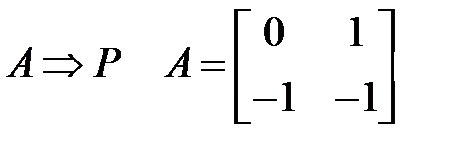
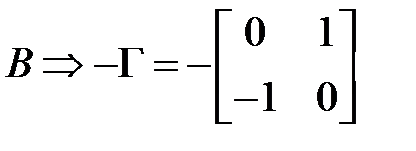
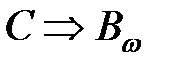
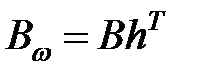
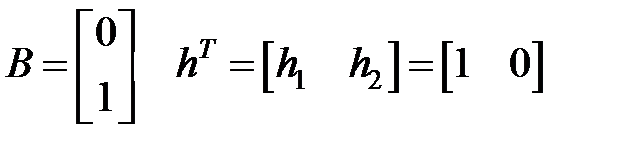
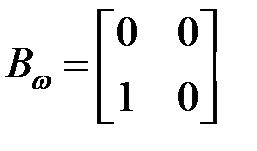
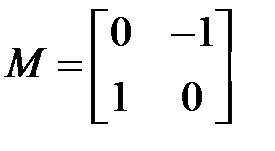
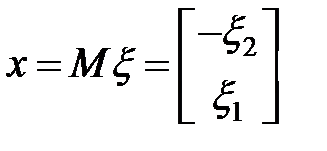
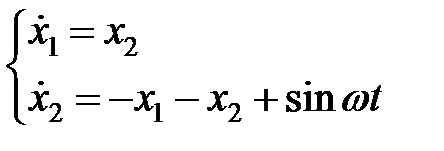
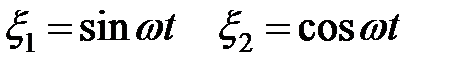 ,
, 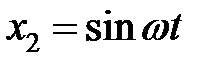 ,
, 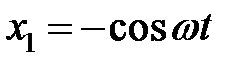
Пример.
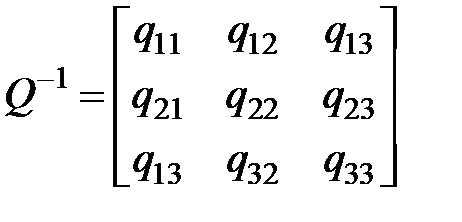
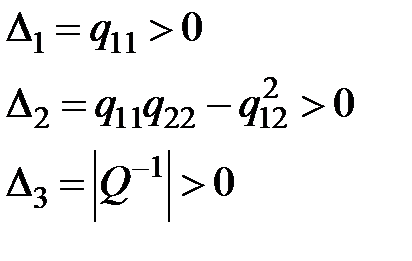
либо возможно переписать
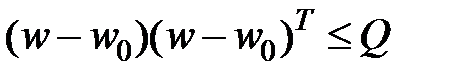
Для хорошей определенности условие Стодола есть нужным и достаточным условием хорошей совокупности.
Умножим справа и слева соответственно на 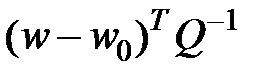 и
и 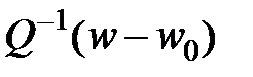
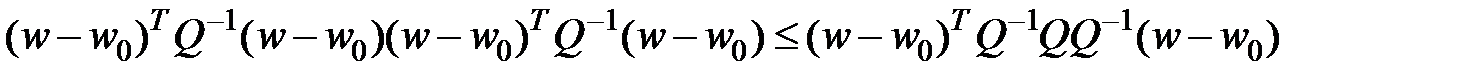
Возьмём
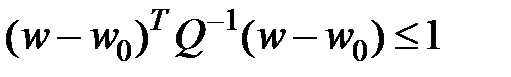 (1)
(1)
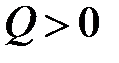
а) 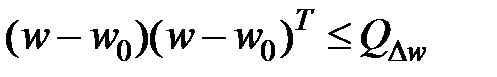 (2)
(2)
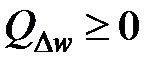
б) 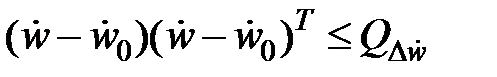
а) и б) являются геометрическими ограничениями для ограниченных хаотических w(t).
В случае, если Q 0, то из (2) направляться (1). В случае, если Q ? 0, то из (2) не обязательно направляться (1). Исходя из этого (2) есть неспециализированной формулой.
Интегральные ограничения:
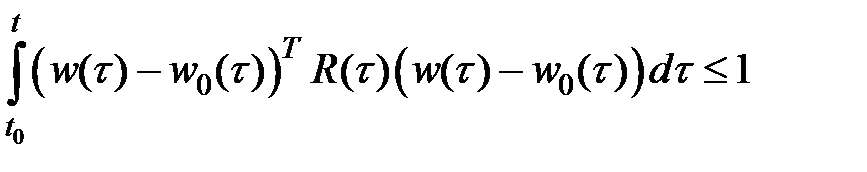 ,
,
т.е. функция 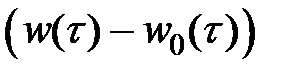 обязана затухать. В случае, если вместо
обязана затухать. В случае, если вместо 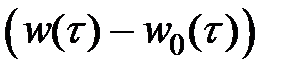 забрать u:
забрать u:
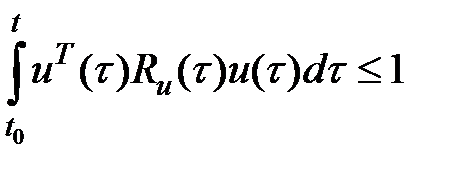 — ограниченное управление, где
— ограниченное управление, где 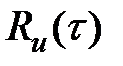 — весовая функция и возможно
— весовая функция и возможно 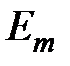 .
.
Геометрическое ограничение 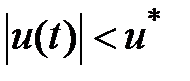 , т.е.
, т.е. 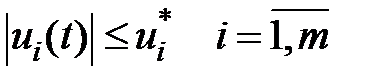
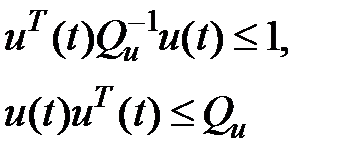
Ограничения бывают и для фазовых координат:
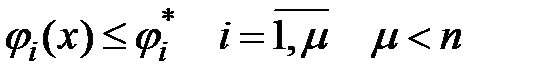
Пример.
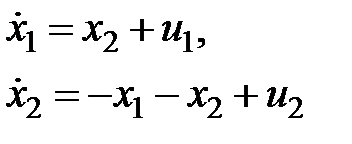
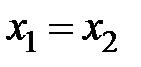 — ограничение,
— ограничение, 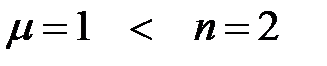 при
при 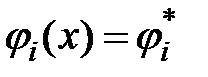
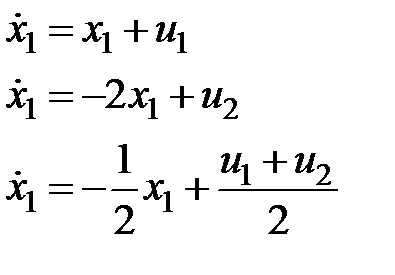
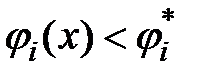
Пример 1.
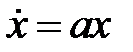
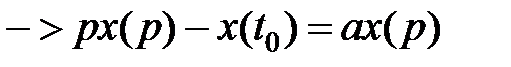
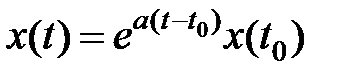
Данному уравнению (1) соответствует n частных ответов.
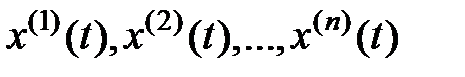
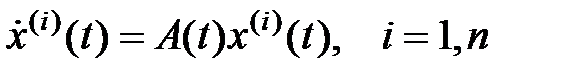 ,
, 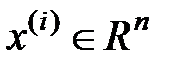
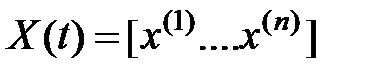
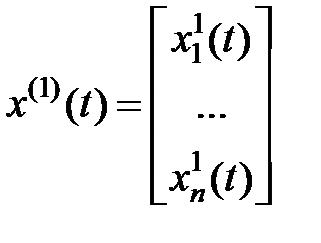
Матрица Х(t) должна быть таковой, что 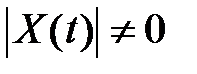 для всех .
для всех .
Пример 2.
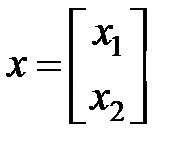 ,
, 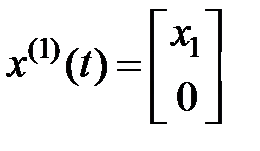 ,
, 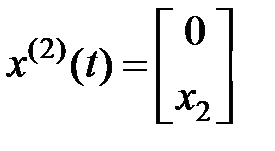 ,
,
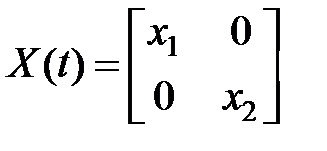 ,
, 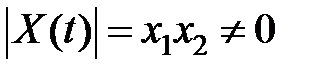 .
.
Тогда ответ уравнения (1) возможно записать в виде 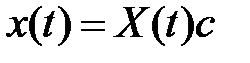 , где
, где 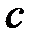 -n-постоянный вектор, которое подставим в уравнение (1), из которого возьмём для любого вектора с уравнение:
-n-постоянный вектор, которое подставим в уравнение (1), из которого возьмём для любого вектора с уравнение:
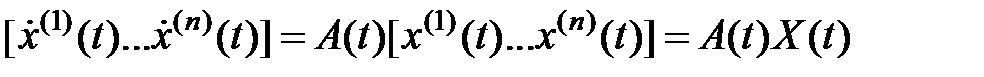 ,
,
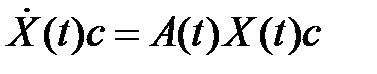 либо
либо 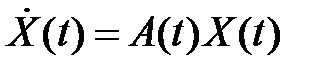
При 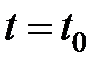 ,
, 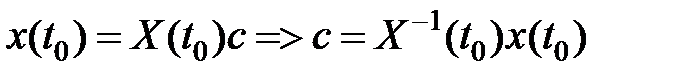
Тогда 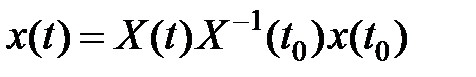 , где
, где 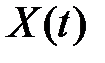 фундаментальная матрица, которая определяется с точностью до постоянной матрицы либо возможно забрана в виде
фундаментальная матрица, которая определяется с точностью до постоянной матрицы либо возможно забрана в виде 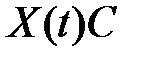 где
где  —
— 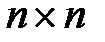 матрица
матрица 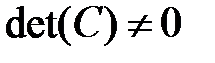 .
.
Вправду, умножим на матрицу  справа:
справа:
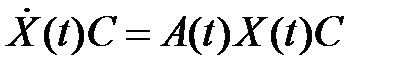 ,
,
обозначим 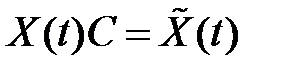 , тогда возьмём
, тогда возьмём 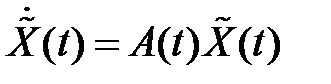 . Наряду с этим ответ
. Наряду с этим ответ
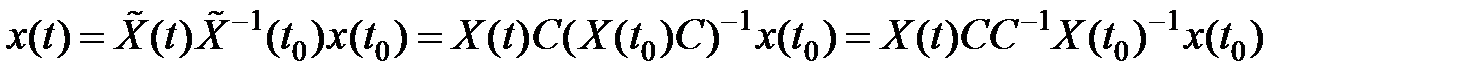 .
.
Обозначим 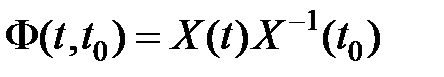 — матрица Коши либо переходная матрица.
— матрица Коши либо переходная матрица.
Тогда
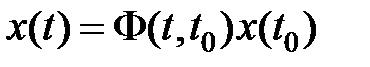
Пример.
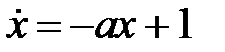
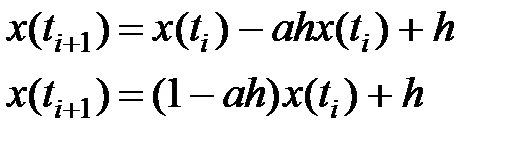

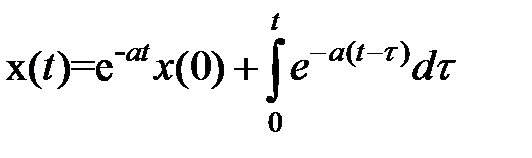
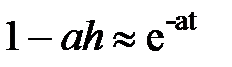
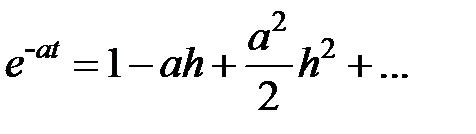
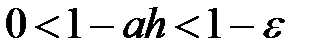
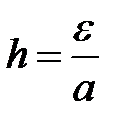
Б) Схема Ракитского
Разглядим разностное уравнение
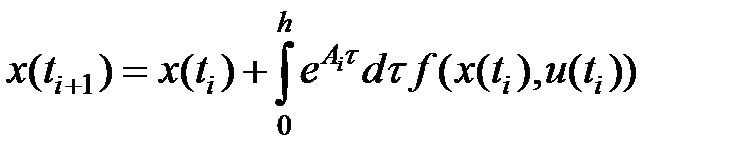 (1)
(1)
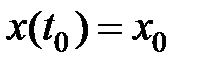
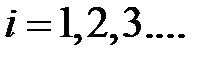
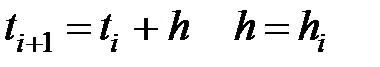
где 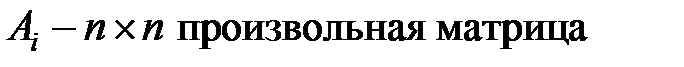 .
.
В случае, если 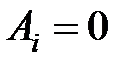 , то возьмём схему Эйлера.
, то возьмём схему Эйлера.
Продемонстрируем, что уравнение (1) дает правильное ответ для уравнения:
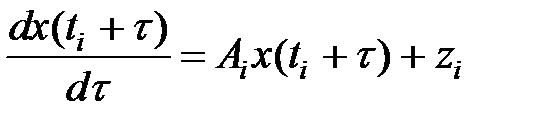 (2)
(2)
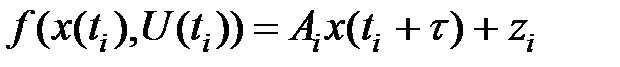
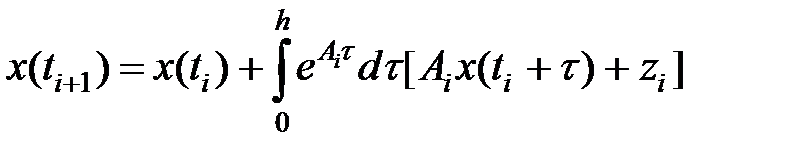 (3)
(3)
Ответ уравнения (2) имеет форму:
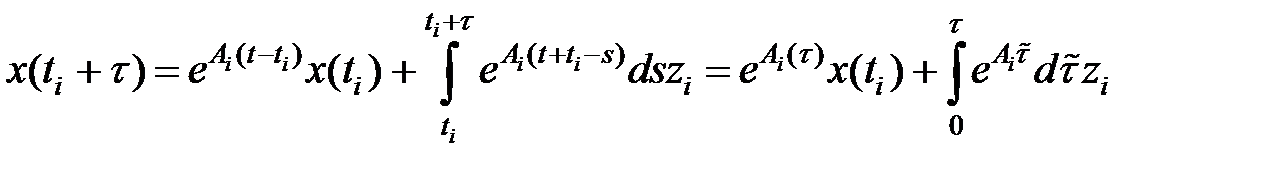
При 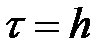 возьмём
возьмём
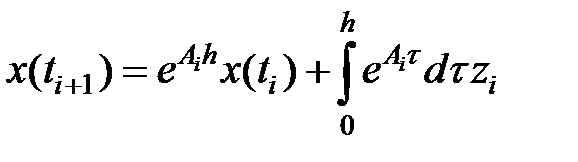
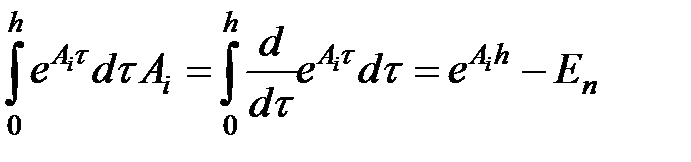
Из уравнения (3) возьмём:
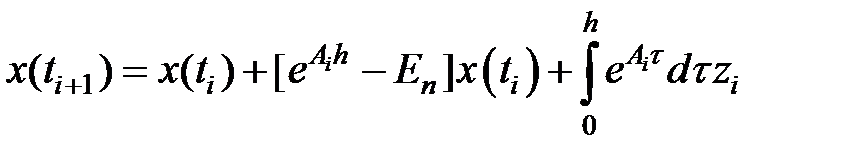
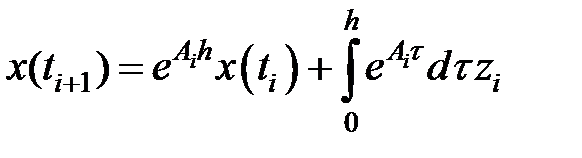
Нужно выбрать 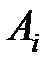
Разглядим однородное уравнение
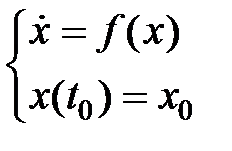
Отыщем производную
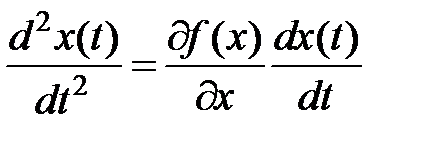
Вычисляем 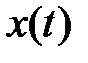 некоей функцией времени
некоей функцией времени
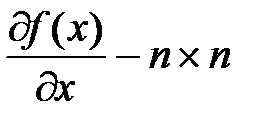 матрица
матрица
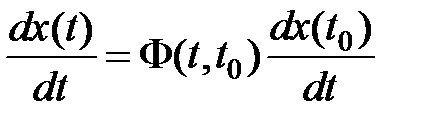
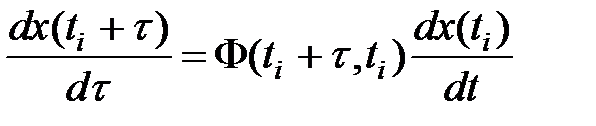
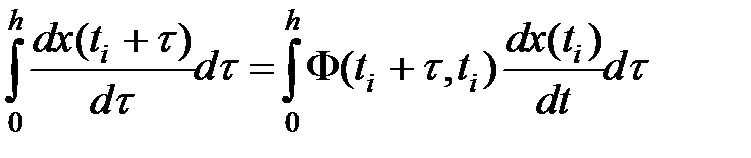
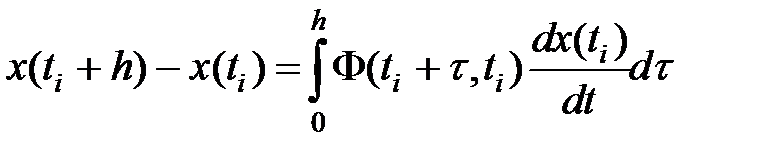
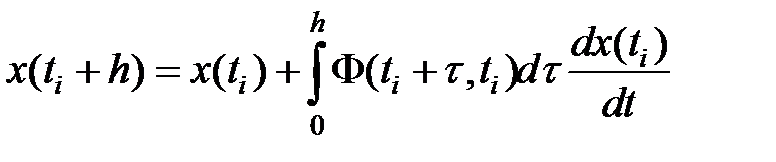 (4)
(4)
Сравним формулу (4) с формулой (1)
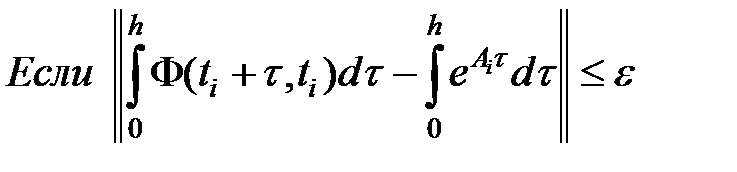
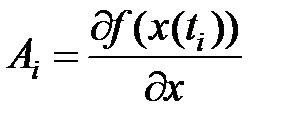
Из этого следует, что матрицу 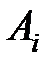 необходимо принять в виде матрицы Якоби. Матрица Якоби берется любой на промежутке
необходимо принять в виде матрицы Якоби. Матрица Якоби берется любой на промежутке 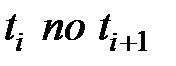 .
.
Так, взяли разностное уравнение.
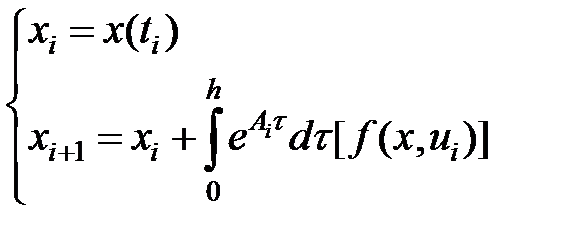
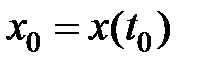
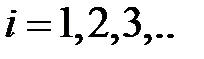
Разглядим случай линейных стационарных совокупностей.
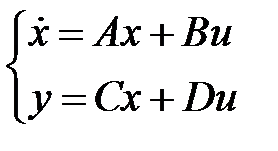
Схема Ракитского (Системный способ 1-го порядка).
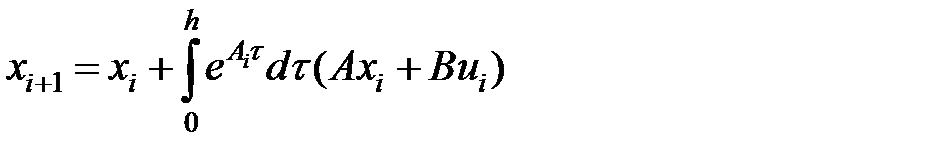
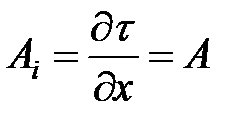
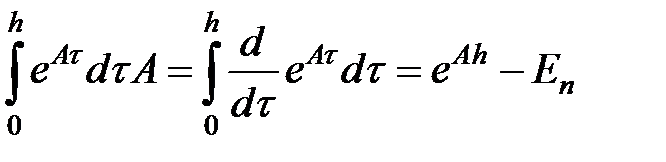
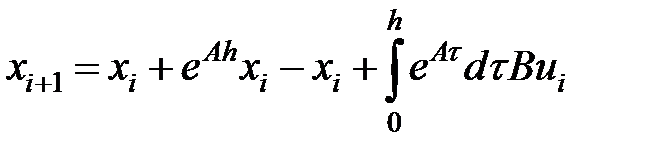
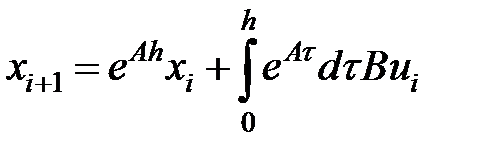
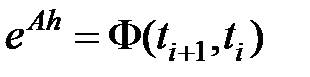
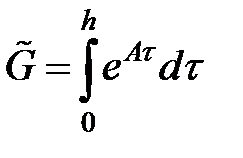
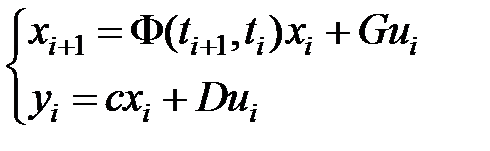
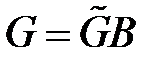
Метод вычисления матриц дискретной модели ( 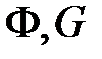 )
)
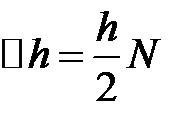
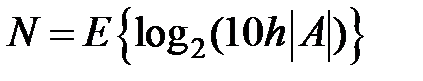 – выделение целой части
– выделение целой части
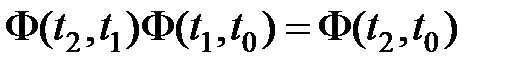
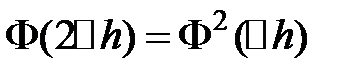
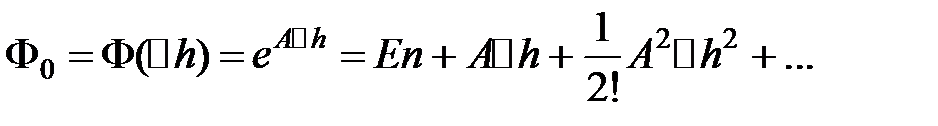
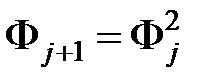
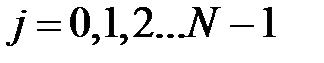
Продемонстрируем, что справедливо равенство:
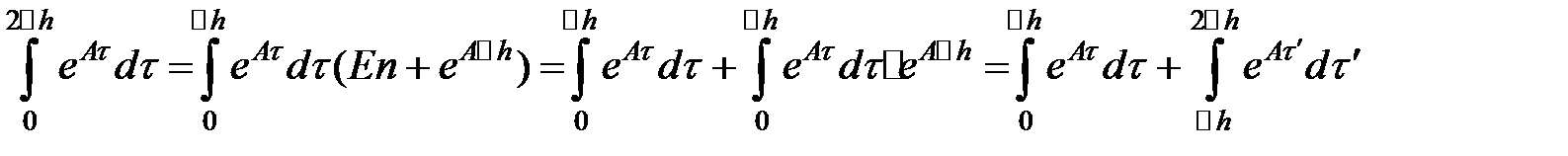
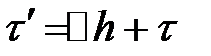
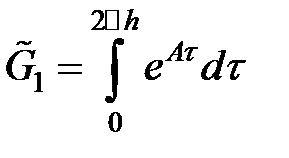
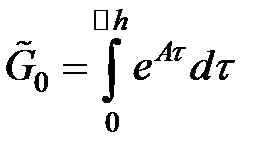
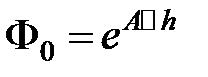
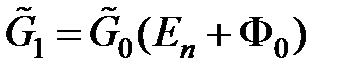
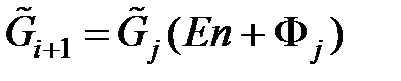
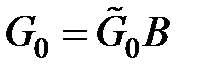
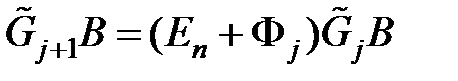 ,
,
где 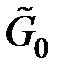 вычисляется по формуле:
вычисляется по формуле:
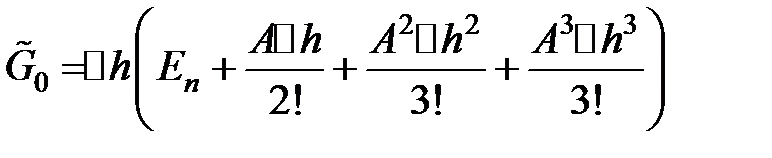
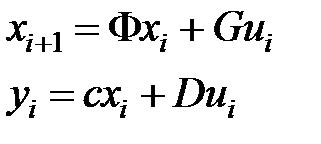
САУ с пассивной адаптацией
САУ с пассивной адаптацией смогут быть использованы в качестве главного контура адаптации.

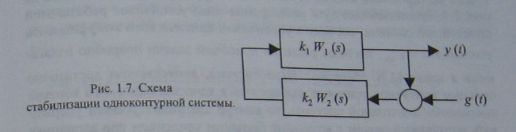

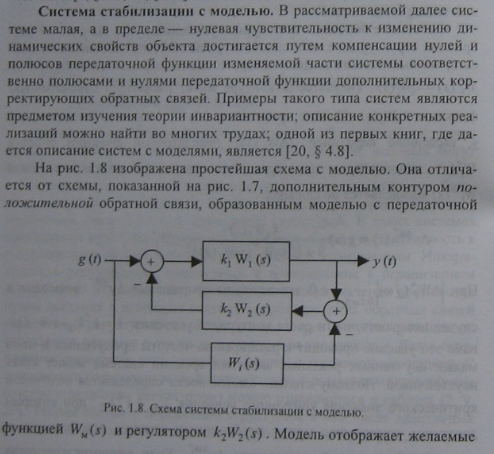

Включeнue.
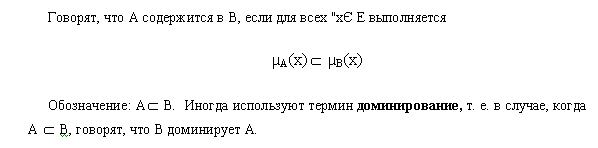
Равенство.
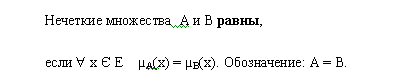
Разность.
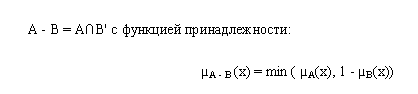
Объединение.

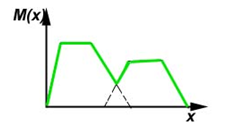
Пересечение.
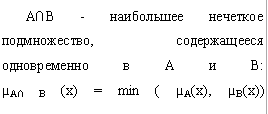
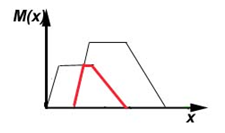
Дополнение.
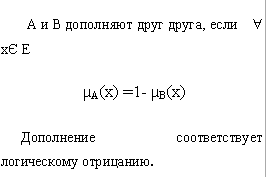
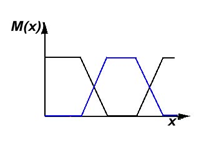
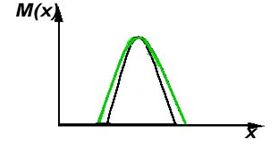
Концентрация.
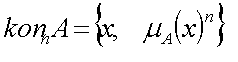
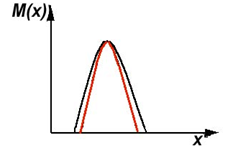
Размывание (либо размытие).
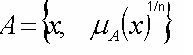

Определение числа термов
Нужно исходить из стоящей перед вами необходимой точности и задачи описания, нужно не забывать, что для большинства приложений достаточно трех термов в переменной;
Нечеткие правила функционирования совокупности должны быть понятны — определяете нужное число термов и каждому из них ставите в соответствие некое значение обрисовываемой физической величины. Для этого значения степень принадлежности физической величины к терму будет равна единице, а для всех остальных значений — в зависимости от выбранной функции принадлежности
Пример 1.
1. Лингвистическая переменная ВОЗРАСТ
для нее термы ЮНОШЕСКИЙ, СРЕДНИЙ и ПРЕКЛОННЫЙ.
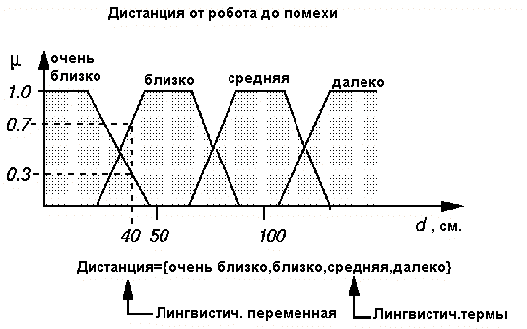
2. Лингвистической переменной Расстояние являются термы На большом растоянии, БЛИЗКО
Нечеткие совокупности основаны на правилах продукционного типа, в качестве заключения и посылки в правиле употребляются лингвистические переменные.
Правило продукций складывается из заключения и посылок.
Допустимо наличие нескольких посылок в правиле, они объединяются при помощи логических связок И, Либо.
Продукционное правило записывается в виде:
«В случае, если (посылка) (связка) (посылка)… (посылка) ТО (заключение)».
Пример 2.
Возможно задать степень принадлежности к терму Весьма БЛИЗКО равную 0.7 , а к терму БЛИЗКО– 0.3
Лекции
«Современная прикладная теория управления»
Модуль 1. Математические модели многомерных САУ