От многомерных probit-моделей отличаются модели множественного выбора. Многомерные probit-модели предполагают принятие нескольких ответов, каждое из которых содержится в выборе одного из двух других вариантов. В моделях множественного выбора необходимо принять одно ответ, но выбрать между тремя и более вариантами. Довольно часто рассматриваются два вероятных типа альтернатив: упорядоченные и неупорядоченные. К примеру, выбор средств добраться до работы (на машине, на метро, на автобусе и т. д.) – выбор среди неупорядоченных вариантов. Выбор ценных бумаг, исходя из их рейтинга, – выбор среди упорядоченных вариантов.
Разглядим сперва модели с неупорядоченными другими вариантами.
В них предполагается, что замечаемое значение выбора t-м индивидуумом j-го варианта (уt=j) связывается со значениями факторов, сопутствующих его выбору, эконометрическим уравнением следующего вида:
уt=h(a¢,ztj)+etj, (10.84)
где h – функция, отражающая темперамент влияния факторов на выбор t-м индивидуумом j-го варианта; etj – неточность модели; a – вектор параметров модели; ztj – вектор свободных переменных –значений факторов, воздействующих на выбор t-го индивидуума, каковые смогут характеризовать самого индивидуума, другой вариант, или и то и другое в один момент. К примеру, при выборе торгового комплекса для приобретения комплекта товаров вектор ztj может иметь следующую структуру:
ztj =(Kj, Rtj, Dt), (10.85)
где Kj – количество магазинов в j-м торговом комплексе; Rtj – расстояние от дома t-го индивидуума до j-го торгового комплекса; Dt – доход t-го индивидуума.
Увидим, что неточности etj (t=1,2,…,Т) модели (10.84) определяются как et1=1–h(a¢,zt1), et2=2–h(a¢,zt2),…, etJ=J–h(a¢,ztJ).
На основании модели (10.84) смогут быть оценены возможности выбора t-м индивидуумом каждого из других вариантов, т. е. Р(уt=1), Р(уt=2),…, Р(уt=J). Для этого должны быть известны:
1) функция h(a¢,ztj);
2) закон распределения неточностей etj.
Предположим, что функция h(a¢,ztj) имеет линейный вид:
h(a¢?ztj)=a¢?ztj=
где – i-я компонента вектора ztj (i=1,…,п).
Соответственно неточности etj (t=1,2,…,Т) модели (10.84) примут следующий вид: et1=1–a¢?zt1, et2=2–a¢?zt2,…, etJ=J–a¢?ztJ.
Предположим, что неточности etj свободны и распределены по обычному закону, тогда возможность выбора t-м индивидуумом j-го варианта определяется следующим образом:
o 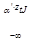 …o
…o 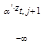 o
o 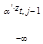 …
…
o 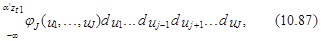
где u1,…, uJ – переменные интегрирования, а плотность совместного распределения неточностей jJ (.) определяется как
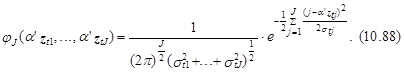
В выражении (10.88)
Из-за сложности вычисления многомерных интегралов в выражении (10.87) модели, основанные на обычном распределении неточностей (probit-модели), не нашли широкого применения в изучениях множественного выбора.
Определение возможностей выбора Р(уt=1), Р(уt=2),…, Р(уt=J) значительно упрощается, в случае, если высказать предположение, что неточности etj свободны и распределены по закону Вейбулла, т. е.
Тогда их совместная плотность распределения возможно представлена в следующем виде:
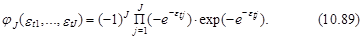
На основании выражения (10.89) возьмём, что возможность выбора выбора t-м индивидуумом j-го варианта определяется как
o …o 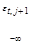 o
o 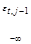 …
…
o 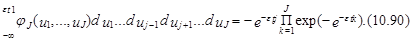
С учетом того, что величина неточности etj зависит от величины –a¢?ztj, и 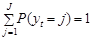 в этом случае совсем имеем:
в этом случае совсем имеем:
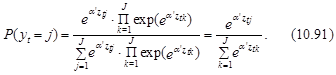
Выражение (10.91) лежит в базе logit-моделей множественного выбора.
Увидим, что при методе формирования свободных факторов, соответствующем выражению (10.85), возможность выбора t-м индивидуумом j-го варианта будет зависеть от тех факторов, каковые отражают характеристики лишь варианта j (число магазинов в j-м торговом комплексе) или совместные характеристики варианта j и индивидуума t (к примеру, расстояние от дома индивидуума до торгового комплекса есть их совместной чёртом).
Это возможно продемонстрировать следующим образом. Представим вектор ztj в следующем виде: ztj =[хtj, wt], где вектор хtj образован факторами, отражающими характеристики варианта j и совместные характеристики варианта j и индивидуума t, а вектор wt – факторами, отражающими только характеристики индивидуума t (к примеру, доход). Вектор параметров a кроме этого представим как совокупность двух векторов a=[a*, b], где a* – вектор коэффициентов, соответствующих свободным переменным хtj, а b – вектор коэффициентов, соответствующих свободным переменным wt. Введя такое представление в модель (10.88), возьмём следующее выражение, определяющее возможность выбора t-м индивидуумом j-го варианта:
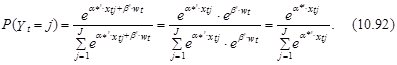
Из выражения (10.92) следует, что свободные переменные wt, каковые характеризуют индивидуума (но не характеризуют другой вариант), вправду не будут оказывать влияние на распределение возможностей выбора.
Для учета влияния показателей личностей в модели (10.91) нужно организовать пара другую структуру векторов ztj, отличающуюся от структуры, определенной выражением (10.85). Вектора ztj должны выглядеть следующим образом:
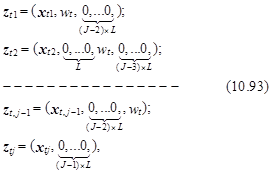
где L – число компонент в векторе wt.
В рассмотренном выше примере, в то время, когда индивидуум с доходом Dt выбирает один из трех торговых комплексов в соответствии с выражением (10.93) вектора ztj примут следующий вид:
zt1=(K1, Rt1, Dt, 0);
zt2=(K2, Rt2, 0, Dt); (10.94)
zt3=(K3, Rt3, 0, 0).
где Kj – число магазинов в j-м торговом комплексе, Rtj – расстояние от дома t-го индивидуума до j-го торгового комплекса.
Так, возможность выбора t-м индивидуумом j-го другого варианта ставится в зависимость и от черт варианта и от черт личностей. Но на практике в большинстве случаев формируются модели, которые содержат лишь какой-либо один комплект однородных факторов. Logit-модель, учитывающая влияние на возможность выбора t-м индивидуумом j-го другого варианта факторов хtj, включающих чертей варианта j и совместные характеристики варианта j и индивидуума t, именуются условной logit-моделью. Увидим, что в условной logit-модели наровне с ранее отмеченными особенностями их распределения и независимости ошибок по закону Вейбулла кроме этого предполагается, что неточности гомоскедастичны.
Для условной logit-модели возможности Р(уt=j), j=1,…,J также будут быть выяснены на базе выражения (10.92). Маржинальные эффекты постоянных свободных переменных х смогут быть взяты методом дифференцирования возможностей по факторам х:
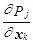 =[Pj?(d–Pk)]?a*, (10.95)
=[Pj?(d–Pk)]?a*, (10.95)
где d=1, в случае, если j=k, и d=0 – в другом случае. (Для избежания путаницы в обозначениях индексы наблюдений тут опущены).
При практическом применении условной logit-модели довольно часто узнается, что предположение о независимости неточностей etj не соответствует действительности. К примеру, при выборе одного из трех торговых комплексов может оказаться, что количество магазинов в первом из них в два раза больше, чем во втором (K1=2K2), но и расстояние до него в два раза больше, чем до второго (Rt1=2Rt2). Неточности et1 и et2 в этом случае определяются как
et2=ln2–a1K2–a2Rt2. (10.96)
Из выражения (10.96) направляться, что неточности являются зависимыми:
et1=–2(ln2–et2). (10.97)
Зависимость неточностей влечет за собой утрату эффективности оценок параметров aусловной logit-модели, взятых при применении “классических” способов оценивания.
К тому же, в случае, если разглядеть пара другую процедуру выбора t-м индивидуумом других вариантов, то неэффективность оценок модели возможно устранить. В частности, это возможно сделать, организовав последовательную процедуру выбора, на каждом шаге которой выбирается одно из двух вероятных ответов. Такая процедура возможно обрисована многомерной probit-моделью, которая возможно представлена в следующем виде:
ytj=a¢?xj+etj
(ytj=1, в случае, если индивидуум t выбрал вариант j;
[e1, e2,…, eJ]~N[0, S]. (10.98)
где xj – вектор свободных переменных, характеризующих j-й вариант, a – вектор параметров модели; ej – неточность модели, распределенная по обычному закону с ковариационной матрицей и нулевым средним S (в общем случае малоизвестной).
Разглядим следующий пример, отражающий особенности применения данного подхода. Предположим, что изучается выбор одного из трех видов транспорта для поездки на работу (автомобиль, автобус, метро). Введем три двоичные переменные соответствующие каждому средству передвижения: y1=1, в случае, если выбран автомобиль, y1=0 для всех остальных видов транспорта; y2=1, в случае, если выбран автобус, y2=0 для всех остальных видов транспорта; y3=1, в случае, если выбрано метро, y3=0 для всех остальных видов транспорта. Требуется оценить следующий комплект возможностей: P(y1=1); P(y2=1) и P(y3=1).
Выбор одного из трех других вариантов возможно обрисовать в виде “дерева” последовательных ответов, в узлах которого происходит двоичный выбор (см. рис 10.3).
 автомобиль
автомобиль
y1=1

 автобус
автобус
y1=0
y2=1
y2=0
метро
Рис.10.3. Последовательность выбора одной из трех альтернатив
В каждом узле, применяя двоичные модели, возможно оценить условную возможность выбора соответствующего варианта. Абсолютная возможность его выбора вычисляется по формуле умножения возможностей. Так, к примеру, абсолютная возможность выбора метро как метода добраться до работы определяется следующим выражением:
P(y3=1)=P(y2=0, y1=0)=P(y2=0)?P(y2=0|y1=0). (10.99)
Возможность P(y2=0) оценивается с применением двоичной probit-модели (10.50), возможность P(y2=0|y1=0) –на базе выражения (10.74)..
Гнездовые logit-модели (nested logit-models).
Как было отмечено, в условной logit-модели неточности в большинстве случаев предполагаются гомоскедастичными. Для практики это предположение довольно часто есть через чур строгим. К примеру, при выбора одного из трех торговых комплексов при условии, что количество магазинов в первом из них в два раза больше, чем во втором (K1=2K2), а расстояние до первого в два раза больше, чем до второго (Rt1=2Rt2), дисперсии неточностей e1 и e2 эконометрической модели, связывающей эти выбора первого и второго торгового комплекса с воздействующими на данный выбор факторами (см. выражение (10.96)), определяются следующим образом:
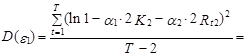
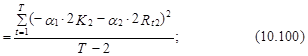
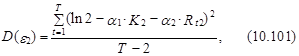
где T – число наблюдений.
В случае, если , то D(e1)¹D(e2), т. е. неточности ej гетероскедастичны.
Один из способов ослабить предположение о гомоскедастичности неточностей в условной logit-модели связан с трансформацией процедуры выбора других вариантов. В этом случае варианты разделяются на непересекающиеся группы так, что в группы дисперсии неточностей etj уравнения (10.84) являются однообразными, а дисперсии неточностей различных групп между собой различаются.
Предположим, что J вариантов смогут быть разбиты на L групп, и неспециализированный комплект вариантов представляется как [1,…,J]=[(1|1,…,J1|1),…, (1|L,…, JL|L)], где j|l – j вариант в группе l, Jl – номер последнего варианта в группе l. Употребляется следующая логика выбора решения. Сперва выбирается одна из L групп, после этого осуществляется выбор варианта в рамках группы. Данный процесс имеет древовидную структуру, которая для двух вариантов и 5 групп может выглядеть следующим образом:
Выбор
Несколько1 Несколько2
1|1 2|1 1|2 2|23|2
Пускай хj|l – вектор свободных переменных, воздействующих на выбор варианта в группы, а zl – вектор свободных переменных, воздействующих на выбор группы.
Если бы для описания процедуры выбора употреблялась условная logit-модель (10.92), то предполагалось бы, что выбор варианта j и выбор группы l не зависят друг от друга.
При условии независимости выбора группы и варианта в группы возможность выбора конкретного варианта определялась бы следующим выражением:
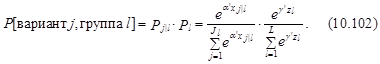
где a и g – вектора параметров.
Для гнездовой logit-модели абсолютную возможность выбора j-го варианта и l-й группы возможно представить как произведение условной возможности выбора j-го варианта при условии, что была выбрана l-я несколько, и абсолютной возможности выбора l-й группы.
Увидим, что потому, что в группы неточности гомоскедастичны, то условную возможность выбора j-го варианта при условии выбора l-й группы, возможно выяснить с применением выражения (10.92) как

Специфика гнездовой logit-модели, ее отличие от условной logit-модели, пребывает в подходе к определению возможности выбора l-й группы. Чтобы раскрыть эту специфику, введем переменную Il, характеризующую “сокровище” l-й группы:

В гнездовой logit-модели “сокровище” l-й группы рассматривается как другой фактор, воздействующий на выбор данной группы, т. е. возможность выбора l-й группы определяется следующим образом:
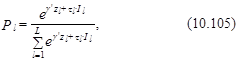
где tl – параметр, что и отличает гнездовую logit-модель от условной logit-модели. В последней он принимает значение 1. Исходя из этого возможность выбора l-й группы в условной logit-модели определяется как

В гнездовой logit-модели значение параметра tl оценивается вместе с параметрами g.
В целом, оценивание абсолютной возможности выбора j-го варианта в l-й группы в рамках гнездовой модели осуществляется следующим образом:
1. Вектор параметров a оценивается с применением условной logit-модели типа (10.92), обрисовывающей выбор j-го варианта в зависимости от факторов хj|l. По окончании оценки параметров a по формуле (10.103) определяется сокровище l-й группы, т. е. Il.
2. Вектор параметров g и параметр tl кроме этого оцениваются с применением условной logit-модели типа (10.92), которая обрисовывает выбор l-й группы в зависимости от факторов zl и Il.
3. По формулам (10.103), (10.105) оцениваются возможности Pj|l и Pl. Абсолютная возможность выбора j-го варианта в l-й группы определяется как произведение Pj|l и Pl.
Уровень качества оценок, приобретаемых на базе гнездовой logit-модели, во многом определяется правильностью построения дерева других вариантов. Напомним, что на практике достаточно тяжело оценить, соответствует ли выбранная структура для того чтобы дерева исходным условиям модели, пребывающих в постулировании определенных допущений относительно дисперсий неточностей (постоянство дисперсий неточностей в группы и различие дисперсий в различных группах).
Как это было продемонстрировано ранее, модификации logit-моделей смогут формироваться в зависимости от состава учитываемых в них факторов. В частности, мультиномиальная logit-модель в отличие от рассмотренных выше модификаций учитывает, что на выбор индивидуума t воздействуют лишь его характеристики. Примером мультиномиальной logit-модели есть модель выбора сферы деятельности (Schmidt and Strauss, 1975). Допустим, что имеется информация: а) довольно вероятной сферы деятельности человека: (0) – “прислуга”, (1) – “светло синий воротничок”, (2) – “ремесленник”, (3) – “белый воротничок”, (4) – “начальник”; б) относительно характеристик индивидуума (факторов): образование, стаж работы в данной области, пол.
Предположим, что значения зависимой переменной yt и свободных факторов wt, связаны следующим образом:
yt=aj¢?wt +etj, (10.107)
где ytнаблюдаемые значения зависимой переменной (т. е. 0, 1,…,J); wt – вектор факторов, содержащий характеристики индивидуума t; aj – вектор параметров, характеризующих влияние факторов wt на выбор конкретного варианта j, etj – неточность модели.
Предположим кроме этого, что неточности etj, j=1,…,J свободны и распределены по закону Вейбулла, т. е.
Тогда возможность выбора t-м индивидуумом j-го варианта возможно представлена в следующем виде (см. выражения (10.89)–(10.91)):
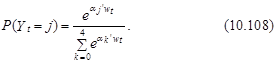
Увидим, что в приведенном примере рассматривается нулевая альтернатива. Это разрешает снизить количество вычислений, потому, что на практике a0 не оценивают, а принимают равным нулевому вектору. Тогда в соответствии с выражению (10.108) возможности выбора t-м индивидуумом варианта j, j=0,1,…, J–1; определяются в соответствии с следующим формулам:
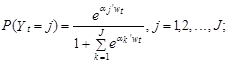
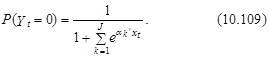
Из выражений (10.109) направляться, что логарифм отношения возможностей выбора j-й и 0-го варианта равен
 |
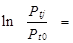 aj¢?wt?, (10.110)
aj¢?wt?, (10.110)
а логарифм отношения возможностей выбора j-го и k-го вариантов –
 |
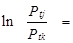 wt¢?(aj–ak). (10.111)
wt¢?(aj–ak). (10.111)
Увидим, что, в случае, если предположение о независимости неточностей etj не выполняется, то соотношения между возможностями нуждаются в определенной корректировке.
Модели с упорядоченными другими вариантами.
Варианты в моделях множественного выбора смогут быть естественным образом упорядочены. Примерами упорядоченных вариантов являются:
1. Рейтинги ценных бумаг.
2. Результаты дегустации.
3. Опросы публичного мнения.
4. Уровни сложности работ.
5. Типы страховых полисов, выбираемых потребителем (отсутствие такового, частичное покрытие, полное покрытие).
6. Степени занятости (безработный, занят часть дня, занят полный сутки).
Во всех этих случаях значения зависимой переменной в большинстве случаев высказывают отношения предпочтения среди других вариантов. Такие отношения смогут быть выражены рангами, имеющими вид упорядоченных комплектов чисел: 0,1,2,… Наряду с этим самый предпочтительному варианту может соответствовать как нуль (в этом случае рейтинги вариантов с ростом их ранга уменьшаются), так и последнее число в данной последовательности J (в этом случае рейтинги альтернатив уменьшаются вместе с уменьшением их ранга).
Для анализа определения предпочтительности выбора среди упорядоченных оценки влияния и альтернативных вариантов на данный выбор разных факторов активно используются порядковые logit- и probit-модели. В таких моделях возможности предпочтения кроме этого, как и в биномиальной probit-модели (10.58), определяются с применением уравнения латентной регрессии:
yt*=a¢?xt+et. (10.112)
где yt* – ненаблюдаемая переменная, которая так же, как и прежде является выгодой (полезность) выбора j-го варианта для t-го индивидуума, к примеру, барыши от приобретения акций с j-м рейтингом; a – вектор параметров; xt – вектор свободных переменных, воздействующих на выбор t-го индивидуума; et – неточность модели.
В случае, если значение переменной уt* удовлетворяет условию уt*
в случае, если yt*?0, то yt=0;
в случае, если 0
в случае, если m1
. . . . . . . . . . . . . . . .
в случае, если mJ–1?yt*, то yt=J. (10.113)
где mj (j=1,2,…,J–1) – малоизвестные параметры, каковые подлежат оценке, как и параметры a (и оцениваются теми же способами). Границы m1,…, mJ–1 возможно трактовать как один из вариантов цензурирования.
Предположим, что неточности et нормально распределены, e~N[0,1]* . С учетом этого комплект возможностей появления j-й замечаемой переменной (j-го ответа) определяется следующими выражениями:
P(yt=0)=F(–a¢?x t);
P(yt =1)=F(m1–a¢?x t)–F(–a¢?x t);
P(yt =2)= F(m2–a¢?x t)–F(m1–a¢?x t);
. . . . . . . . . . . . . . . . . . . . . . . . . . (10.114)
P(yt =светло синий)=1–F(mJ–1–a¢?x t).
где F(.) – функция закона стандартного обычного распределения.
Из выражений (10.114) направляться, что эти возможности Р(yt =j), j=0,…,J будут хорошими, в случае, если выполняется следующее условие:
0
На рис. 10.4 продемонстрировано распределение возможностей выбора конкретных альтернатив.
Разглядим изюминке определения маржинальных эффектов факторов хt, каковые будут характеризовать изменение возможности выбора j-го другого варианта при трансформации одного из свободных факторов на 1 единицу. Допустим, имеется три варианта (данный случай предполагает лишь один параметр положения m). В соответствии с выражением (10.114) возможности выбора каждого из вариантов определяются как
P(yt=0)=F(–a¢?xt);
P(yt=1)= F(m–a¢?xt)–F(–a¢?xt);
P(yt=2)=1–F(m–a¢?xt) (10.116)
| et |
| a¢xt |
| m3–a¢xt |
| m1–a¢xt |
| yt=3 |
| yt=0 |
| m2–a¢xta¢x a¢x |
| yt=4 |
| yt=2 |
| yt=1 |
| f(et) |
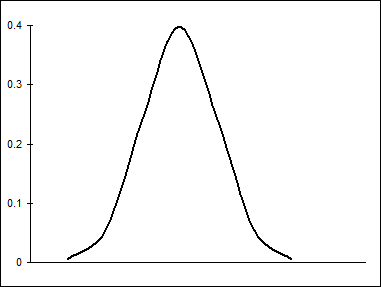
Рис.10.4. Возможности в упорядоченной probit-модели.
Тогда маржинальные эффекты факторов определяются в соответствии с следующему выражению:
¶P[yt=0]/¶xt=–j(a¢?xt)?a;
¶P[yt=1]/¶xt=[j(–a¢?xt)–j(m–a¢?xt)]?a;
¶P[yt=2]/¶xt=j(m–a¢?xt)?a. (10.117)
где j(.) – функция плотности распределения стандартной обычной переменной.
На рис. 10.5 целой линией нарисовано распределение yt в зависимости от неточности et. Рисунок характеризует маржинальный эффект при повышении одного из факторов хit (i=1,2,…, n) при неизменных a и m. Данный эффект эквивалентен смещению графика распределения вправо, что продемонстрировано пунктирной линией.
| yt=2 |
| yt=1 |
| yt=0 |
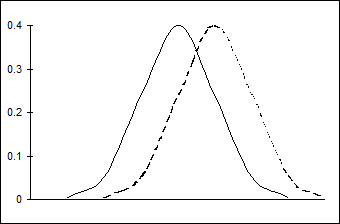
Рис.10.5. Влияние трансформации хt на оцененные возможности.
В соответствии с первому выражению в (10.117) изменение возможности выбора 0-го варианта зависит от коэффициента при факторе хi. В случае, если коэффициент ai хорош (для данного комплекта хt), то возможность P[yt=0] обязана снизиться (производная ¶P[yt=0]/¶хit имеет символ, противоположный символу ai). Соответственно, в случае, если коэффициент ai отрицателен, то возможность P[yt=0] обязана повыситься.
В соответствии с третьему выражению в (10.117) направление трансформации возможности P[yt=2] при повышении фактора хi, кроме этого определяется знаком коэффициента ai: но в этом случае при положительном ai возможность возрастает, при отрицательном ai – значительно уменьшается.
Увидим, что в соответствии с второму выражению в (10.117) изменение возможности P[yt=1] зависит не только от символа ai, но и от символа, что будет иметь разность двух плотностей [j(–a¢?xt)–j(m–a¢?xt)]. В случае, если эти символы совпадают, что возможность P[yt=1] возрастает с повышением хit, если не совпадают, то она значительно уменьшается.
Модели счетных данных
В практических изучениях достаточно довольно часто приходится сталкиваться с зависимыми переменными, каковые являются результатами подсчетов. Примерами таких переменных являются число выданных за год патентов, количество выпускников институтов, число аварий на судах и т. д. Эконометрическая модель в этом случае связывает количество случившихся событий (у) с факторами, характеризующими условия, сопровождавшие эти события.
Дискретный темперамент зависимой переменной дает основание предполагать, что линейные модели, связывающие число событий с уровнями сопровождающих их факторов, будут не совсем адекватны настоящим данным по причине того, что расчетные значения смогут принимать каждые, не обязательно целые значения. В таких обстановках более приемлемыми являются модели другого типа, например, модель регрессии Пуассона.
Зависимость числа событий уt, случившихся за фиксированный временной промежуток (t, t+1) (сутки, семь дней, месяц), от значений воздействующих на это число факторов в соответствии с данной модели представляется следующим образом:
где a – вектор параметров уравнения; xt – вектор свободных переменных, характеризующих условия появления событий; et – неточность уравнения;
. (10.119)
Предполагается, что число событий уt распределено по закону Пуассона с параметром lt.
С учетом этого возможность осуществления каждого числа событий уt возможно выяснена в соответствии с следующему выражению:
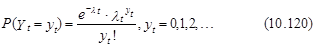
Увидим, что в соответствии с (10.118) при нулевом математическом ожидании неточности условное математическое ожидание числа событий для заданного комплекта значений факторов xt определяется как
В соответствии с модели Пуассона условное условная дисперсия и математическое ожидание при заданных значениях факторов xt равны между собой:
С учетом (10.121) маржинальный эффект факторов возможно оценен следующим образом:
¶M[y |xt]/ ¶xt=lt?a. (10.123)
Разглядим изюминке формирования модели Пуассона для случаев цензурирования и усечения исходных значений зависимой переменной уt.
Цензурированной выборке отвечает следующий пример. Предположим, что модель обрисовывает количество событий, характеризующих частоту визита доктора респондентами в прошедшем сезоне. Варианты ответов: 0, 1, 2, 3 и более. Всем ответам, имеющим значение более 2, присваивается значение 3. Цензурированные выборки в большинстве случаев приобретают методом объединения последовательности значений с низкой возможностью появления в одно.
В соответствии с закону Пуассона для цензурированной выборки возможности того, результирующий показатель уt принимает конкретное значение (j=0,1,2…), определяются как
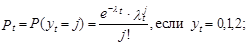
Усеченные комплекты значений зависимой переменной уt характеризуют обстановку, в то время, когда одно либо несколько значений высказывают своеобразное содержание (хорошее от того, которое выражено вторыми значениями). К примеру, задан вопрос: “какое количество раз вы посещали курорты в прошедшем году?” Ответ “0” может обозначать отсутствие денег, времени либо принципиальное нежелание убивать время так. Ненулевые значения ответов говорят о жажде убивать время так. При таких условиях эконометрическая модель может отражать зависимость частоты посещений курорта от факторов жизнедеятельности индивидуума с учетом элиминирования его неприятия курорта как места отдыха.
В случае, если модель формируется для оценки возможностей принятия переменной уt лишь хороших значений (т. е. ее нулевые значения усекаются), то в соответствии с (10.120) выражения, определяющие эти возможности имеют следующий вид:
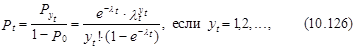
где показатель lt выяснен в соответствии с выражением (10.119).