Ниже будет обрисована действенная процедура, дающая ответ на вопрос, есть ли эта формула тождественно-подлинной. Эффективность свидетельствует, что процедура даёт ответ для каждой формулы в конечное число шагов.
Мысль способа аналитических такова: тождественную истинность формулы мы будем обосновывать опровержением допущения о ее ложности. В этом доказательстве от противоположного, табличные правила организуют систематический поиск контрпримеров для допущения о ложности. Таблицу легко взять, совершив на листе бумаге вертикальную линии. Справа от черты мы будем помещать формулы, каковые, в соответствии с правилами, каковые будут приведены ниже, оцениваются как фальшивые. Слева от черты, наоборот, будут помещены формулы, оцениваемые как подлинные.
Пускай нам нужно узнать, есть ли некая формула А тождественно-подлинной. Для этого записываем ее справа от черты. Это будет означать, что она фальшива – в этом состоит отечественное допущение доказательства от противоположного. После этого разворачивается процедура табличного построения, которая протекает правильно редукции и порождает множество таблиц.
Табличные правила (правила редукции). В формулировках табличных правил мы будем применять следующие обозначения:
– стрелки будут обозначать переход от одного состояния некоей таблицы к второму либо от одной таблицы к второй;
– А – редуцируемая на данном шаге формула;
– S – множество (допустимо безлюдное) нередуцируемых на данном шаге формул, находящихся в левой части таблицы;
– G – множество (допустимо безлюдное) вторых нередуцируемых на данном шаге формул, находящихся в правой части таблицы.
Таблицы нумеруются в порядке, что будет выяснен процедурой редукции.
Правила редукции делятся на «левые» и «правые». Формулируем их попарно для каждой связки. За каждым правилом направляться пояснение.
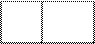
Правило «отрицание справа». В случае, если А имеет форму OВ и находится в правой части таблицы с номером n, то вычеркиваем А и записываем В в левую часть данной же таблицы:
(п) (п)

S OВ, G В, S G
Переход обосновывается определением истинности дляOВ:еслиOВ ложно, то В действительно.
Правило «отрицание слева».В случае, если А имеет форму OВ и находится в левой части таблицы, то вычеркиваем А и записываем В в правую часть данной же таблицы.
(п) (п)
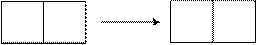
OВ, S GS В, G
ИстинностьOВ свидетельствует ложность В.
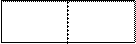
Правило «конъюнкция справа».В случае, если А имеет форму (В U С) и находится в таблице с номером n, то вычёркиваем всю эту таблицу и переходим к рассмотрению двух таблиц с номерами n.1 и n.2, а таблицу n вычеркиваем. Наряду с этим
в n.1 записываем слева S, а справа В, G.
в n.2 записываем слева S, а справа С, G.
(n)
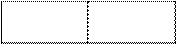 |
S (В U С), G
(n.1) (n.2)
 |
|||
 |
|||
S В, G S С, G
В действительности, ложность (В U С) свидетельствует, что или В ложно, или С ложно, или оба они фальшивы. Достаточно разглядеть первые два случая, что соответствует двум подтаблицам. Другие же формулы из таблицы n переходят в подтаблицы n.1 и n.2 с теми же значениями, т. е. слева – налево, справа – направо.[21]
Правило «конъюнкция слева».В случае, если А имеет форму (В U С) и находится в левой части таблицы, то вычеркиваем А и записываем в эту же часть таблицы В и С.
(n) (n)
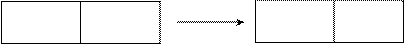
(В U С), S G В, С, S G
Истинность(В U С)равносильна истинности В и истинности С.
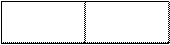
Правило «не сильный дизъюнкция справа». В случае, если А имеет форму (В U С) и находится в правой части таблицы, то вычеркиваем (В U С) и записываем в ту же часть таблицы В и С.
(n) (n)
 |
 |
||
S (В U С), G S В, С, G
(В U С)ложно в то время, когда В ложно и С ложно.
Правило «не сильный дизъюнкция слева». В случае, если А имеет форму (В U С) и находится в левой части таблицы n, то вычёркиваем эту таблицу переходим к рассмотрению таблиц n.1 и n.2, а таблицу n вычеркиваем. Наряду с этим:
записываем в n.1 слева В, S, а справа – G
записываем в n.2 слева С, S, а справа – G.
(n)
 |
(В U С), S G
(n.1) (n.2)
 |
|||
 |
|||
В, SG С, SG
Истинность (В U С) равносильна истинности по крайней мере одной из формул В и С. К рассмотрению каждого из этих случаев мы и переходим в подтаблицах. Другие формулы исходной таблицы переходят в новые таблицы с тем же значением.
Правило «строгая дизъюнкция справа». В случае, если А имеет форму (В ? С) и находится в правой части таблицы n, то вычёркиваем эту таблицу переходим к рассмотрению таблиц n.1 и n.2, а таблицу n вычеркиваем. Наряду с этим:
записываем в n.1 слева В, С, S, а справа – G,
записываем в n.2 слева S, а справа – В, С, G.
(n)
 |
S (В ? С), G
(n.1) (n.2)
 |
|||
 |
|||
В, С, SG S В, С, G
В действительности, ложность (В ? С) равносильна или одновременной истинности В и С, или их одновременной ложности. К рассмотрению каждого из этих случаев мы и переходим в подтаблицах. Другие формулы исходной таблицы переходят в новые таблицы с тем же значением.
Правило «строгая дизъюнкция слева». В случае, если А имеет форму (В ? С) и находится в левой части таблицы n, то вычёркиваем эту таблицу переходим к рассмотрению таблиц n.1 и n.2, а таблицу n вычеркиваем. Наряду с этим:
записываем в n.1 слева В, S, а справа – С, G,
записываем в n.2 слева С, S, а справа – В, G.
(n)
 |
(В ? С), S G
(n.1) (n.2)
 |
|||
 |
|||
В, S С, G С, S В, G
Вправду, истинность (В ? С) равносильна или случаю, в то время, когда В действительно, а С ложно, или случаю, в то время, когда С действительно, а В ложно. К рассмотрению каждого из этих случаев мы и переходим в подтаблицах. Другие формулы исходной таблицы переходят в новые таблицы с тем же значением.
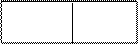
Правило «импликация справа».В случае, если А имеет форму (В ? С) и находится в правой части таблицы, то вычеркиваем А и записываем В в левую часть таблицы, а С – в правую часть.
(n) (n)
 |
|||
 |
S (В ? С), G S, В С, G
(В ? С)ложно, в то время, когда В действительно, а С ложно.
Правило «импликация слева». В случае, если А имеет форму (В ? С) и находится в левой части таблицы n, то вычёркиваем эту таблицу и переходим к рассмотрению таблиц п.1 и n.2. Наряду с этим:
записываем в n.1 слева S, а справа – В, G
записываем в n.2 слева С, S, а справа – G.
(n)
 |
(В ? С), S G
(n.1) (n.2)
 |
|||
 |
|||
С, SG S В, G
Истинность (В ? С) свидетельствует, что или В ложно, или С действительно, или то и второе в один момент. Достаточно разглядеть первые два условия, что мы и делаем в подтаблицах. Другие формулы исходной таблицы переходят в новые таблицы с теми же значениями.
Правила «эквиваленция справа» и «эквиваленция слева» зеркальны относительно правил «строгая дизъюнкция слева» и «строгая дизъюнкция справа» соответственно. Читатель может сформулировать их самостоятельно.
Таблица именуется замкнутой, в случае, если существует формула В, находящаяся в один момент в правом и левом ее столбцах. В замкнутой таблице процесс применения правил редукции останавливается.
Табличное построение. Табличное построение для формулы А появляется при исполнении последовательности шагов:
Ход 1. Записываем А справа в таблицу, нумеруемую как 1.
Ход 2. Используем одно из «правых» правил в зависимости от вида А.
Ход 3. В каждой из оказавшейся по окончании шага 2 таблиц используем одно из правил редукции.
Действуем потом , пока на некоем шаге n построения обнаружится, что ни в одной таблице порожденной на протяжении построения множества таблиц запрещено уже применить правил редукции. Это указывает, что любая таблица Т данного множества либо (а) замкнута, либо (б) не имеет формул, каковые смогут быть редуцированы.
Критерий тождественной истинности формулы А: В случае, если табличное построение для А остановилось и любая невычеркнутая таблица порожденного множества таблиц замкнута, то формула А общезначима. Содержательно это указывает, что предположение о ложности А ведет к несоответствиям при разборе всех вероятных частных случаев.
Приведём пара примеров (номера таблиц, где быть может, опускаем).
Разглядим тавтологию, имеющую наименование «закон Пирса»: ((А E В) E А) E А.
(1)
 |
((А E В) E А) E А
 |
(А E В) E А А (?справа)
(1.1) (1.2)
 |
|||
 |
А А (А E В) А (?слева)
замыкание
(1.2)

А В, А (?справа)
замыкание.
Итак, тут все невычеркнутые таблицы замкнулись, что говорит нам о том, что предположение о ложности закона Пирса несостоятельно.
Разглядим тавтологию, показывающую сообщение слабой дизъюнкции и импликации –
(А ? В) ? (OА U В).
(1)
 |
(А ? В) ? (OА U В)
(1.1) (1.2)
 |
 |
||
(А ? В) (OА U В) (OА U В) (А ? В) (? справа)


(А ? В) O А, В (U справа) (OА U В), А В (? справа)

(А ? В), А В (O справа) (1.2.1) (1.2.2)


OА, А В В, А В (U слева)
(1.1.1) (1.1.2) замыкание
 |
 |
||||
 |
|||||
В, А В А А, В (? слева) А А, В (O слева)
замыкание замыкание замыкание
Тут кроме этого взяты замыкания во всех невычеркнутых таблицах.
Разглядим сейчас пример формулы, которая не есть тождественно подлинной:
(А ? (В U С)) ? (OВ ? OА)
(1)
 (А ? (В U С)) ? (OВ ? OА)
(А ? (В U С)) ? (OВ ? OА)
 |
(А ? (В U С)), OВ OА (? справа, 2 раза)
 (А ? (В U С)), А В (O справа и слева)
(А ? (В U С)), А В (O справа и слева)
(1.1) (1.2)
 |
 |
||
В U С, А В А А, В (? слева)
 замыкание
замыкание
(1.1.1) (1.1.2)


В, А В С, А В (U слева)
замыкание
Одна невычеркнутая таблица осталась незамкнутой – (1.1.2). По ней легко выяснить, при каких условиях исследуемая нами формула окажется фальшивой. Для этого нужно, дабы А и С приняли значение И, а В – значение Л. Выстроим соответствующую строчок таблицы истинности для формулы (А ? (В U С)) ? (OВ ? OА):
| А | В | С | OА | OВ | В U С | А ? (В U С) | OВ ? OА | (А ?(В U С)) ? (OВ ? OА) |
| … | ||||||||
| И | Л | И | Л | И | И | И | Л | Л |
| … |
Мы видим, что формула тут принимает значение Л.
Итак, для всякой формулы, которая воображает нам структуру сложного суждения, возможно решить вопрос о том, есть она тождественно-подлинной либо нет. Любопытно, что из нескончаемого числа тождественно-подлинных формул не все содержательно занимательны. Мы приводили примеры формул, каковые соответствуют закону исключённого третьего и закону несоответствия – (А U OА) и O(А U OА) – их содержательная сокровище очевидна. Но, к примеру, о чём говорит рассмотренный выше закон Пирса, не совсем ясно. Дело в том, что все тождественно-подлинные формулы эквивалентны друг другу, т. е., в каком-то смысле, высказывают одно да и то же, но различными методами. Как это происходит читатель может узнать, познакомившись с более особой литературе по логике, детально освещающей логику высказываний (см. перечень литературы). Принципиально важно, тем ни менее, осознавать, что отвергнув хотя бы одну тождественно-подлинную формулу как «не занимательную», мы тем самым, лишимся и всех остальных.
Упражнения
1. Выстройте таблицы истинности для следующих формул.
1) OА ? OOOА
2) (А U А)? А
3) (А U B)? O(OА U В)
4) (С ? (OС U А)) ? OА
5) (OА ? (В ? С)) ? (OС ? А)
6) (А U O(В U С)) ? O(C ? А)
7) (В ? (С U OА)) U (OВ ? OС)
 (((В U С) ? O(D ? С)) ? А)U OВ
(((В U С) ? O(D ? С)) ? А)U OВ
9) С ? ((OС U В) ? А)
10) ((С ? OА) U (В ? OА)) ? (O(С U В) ? А)
2. Посредством таблиц истинности обоснуйте тождественно-подлинный темперамент следующих формул.
1) А ? OOА
2) (А U А)? А
3) А ? А
4) А ? А
5) ((А U В) U А) ? А
6) ((А U В) U А) ? А
7) ((А ? В) U (В ? А)) ? (А ? В)
 ((А U В) U (OА U OВ)) ? (А ? В).
((А U В) U (OА U OВ)) ? (А ? В).
3. Посредством аналитических таблиц продемонстрируйте, что следующие формулы являются тождественно-подлинными
1) А ? (В ? А)
2) (А ? В) ? (OА ? OВ)
3) O(А ? В) ? (А U OВ)
4) O(А U В) ? (OА U OВ)
5) O(А U В) ? (OА U OВ)
6) (А ? (В ? С)) ? ((А ? В) ? (А ? С))
7) (В ? А) ? ((С ? А) ? (OА ? (В ? OС)))
 ((В ? А) U (С ? А)) ? ((В U С) ? А).
((В ? А) U (С ? А)) ? ((В U С) ? А).
4. Ниже представлены фрагменты работы «О значении и смысле» одного из основоположников современной логики Готтлоба Фреге (1848–1925). Ознакомьтесь с ними и постарайтесь дать ответ на вопрос о том, по какой причине Фреге объявляет значением (денотатом) предложения не обрисовываемую предложением обстановку (факт либо положение дел в мире), а его истинностное значение.
… под «знаком» и «именем» я осознаю любое обозначение, воображающее собою собственное имя, чьим значением, значит, есть определенный предмет (в самом широком смысле этого слова), но не понятие и не отношение, на которых я подробнее остановлюсь в второй статье. Обозначение единичного предмета может кроме этого складываться из нескольких слов или других знаков. Пускай каждое такое обозначение для краткости носит название собственного имени.
Суть собственного имени осознаёт любой, достаточно опытный язык либо совокупность обозначений, к у которых в собствености имя …; тем самым, но, значение, если оно имеется, освещено все же лишь с одной стороны. Всестороннее познание данного значения состояло бы в том, что мы имели возможность бы для каждого заданного смысла указать, относится ли он к этому значению. Этого мы ни при каких обстоятельствах не достигаем.
Сообщение, существующая, в большинстве случаев, между знаком, его его значением и смыслом, такова, что символу соответствует определенный суть, а этому последнему – определенное значение, в то время как одному значению (одному предмету) соответствует не единственный символ. … Возможно, направляться признать, что всякое грамматически верно выстроенное выражение, делающее роль собственного имени, постоянно имеет суть. Но это не означает, что смыслу постоянно соответствует некое значение. Слова «самое удаленное от Почвы небесное тело» имеют некоторый суть; но очень вызывающе большие сомнения, дабы они имели значение. … Из этого следует, что в случае, если мы понимаем суть, это еще не означает, что мы с уверенностью располагаем и некоторым значением.
…
Значение собственного имени – это сам предмет, обозначенный этим именем; представление, которое наряду с этим у нас появляется, в полной мере субъективно; между представлением и значением возможно поместить суть, что, в отличие от представления, не смотря на то, что и не есть субъективным, все же не есть сам предмет.
…
До сих пор мы разглядывали значение и смысл лишь таких выражений, слов, знаков, каковые нами были названы собственными именами. Поставим сейчас вопрос о значении и смысле целого утвердительно-повествовательного предложения. Такое предложение содержит некую идея… Как направляться разглядывать эту идея – как суть предложения либо как его значение? Предположим, предложение имеет значение. В случае, если мы заменим в нем какое-либо слово вторым словом, имеющим то же значение, но второй суть, то это не должно иметь никакого влияния на значение предложения. Но мы видим, что идея в этом случае изменяется; так, к примеру, идея, содержащаяся в предложении «Утренняя звезда имеется тело, освещаемое Солнцем», хороша от мысли, имеющейся в предложении «Вечерняя звезда имеется тело, освещаемое Солнцем». Тот, кто не знает, что Вечерняя звезда имеется Утренняя звезда, имел возможность бы вычислять одну идея подлинной, а другую фальшивой. Значит, идея не может быть значением предложения, наоборот, мы должны вычислять ее смыслом предложения. Но как же обстоит дело со значением? Имеем ли мы право по большому счету ставить о нем вопрос? Возможно, предложение, забранное как целое, имеет лишь суть, но не имеет значения? …
Но отчего же мы желаем, дабы каждое собственное имя имело не только суть, но и значение? По какой причине идея не удовлетворяет нас? Потому и постольку, по какой причине и потому, что для нас принципиально важно истинностное значение мысли. Так бывает не всегда. К примеру, в то время, когда мы принимаем эпическое произведение, нас очаровывает, не считая благозвучия языка, лишь суть предложений и вызываемые ими чувства и представления. Если бы мы поставили вопрос об истине, мы утратили бы эстетическое удовольствие и перешли к научному изучению. … Итак, рвение к истине – вот что постоянно побуждает нас к переходу от смысла к значению.
Мы видели, что для предложения нужно постоянно доискиваться значения тогда, в то время, когда речь заходит о значении составных частей; а это имеет место тогда, и лишь тогда, в то время, когда мы ставим вопрос о его истинностном значении.
Так, мы принуждены признать в качестве значения предложения его истинностное значение. Под истинностным значением – значением истинности предложения я осознаю то, что оно или действительно, или ложно. Вторых значений истинности не бывает. Для краткости я именую одно из этих значений – истиной, истинностью, а второе – ложью, ложностью. На каждое утвердительно-повествовательное предложение, довольно которого ставится вопрос о значении его слов, нужно, так, наблюдать как на собственное имя, причем на такое, значение которого, в случае, если таковое существует, имеется или истина, или неправда. Эти два предмета будут считаться – возможно лишь молчаливо – всяким, кто выносит суждение, кто вычисляет хотя бы что-нибудь подлинным; значит, они будут считаться кроме того скептиком. …
В случае, если отечественное предположение, что значение предложения имеется его истинностное значение, правильно, то последнее должно остаться без трансформации, в случае, если заменить часть предложения выражением, имеющим то же значение, но второй суть. Но так дело и обстоит. … Что же еще, не считая значения истинности, возможно отыскать для того чтобы, что, будучи свойственно самым неспециализированным образом каждому предложению, довольно которого ставится вопрос о значении его составных частей, оставалось бы без трансформации при замене указанного рода?
Потом. В случае, если значение истинности предложения имеется его значение, то, с одной стороны, все подлинные предложения имеют одно да и то же значение, а иначе, одно да и то же значение имеют и все фальшивые предложения. Из этого видно, что в значении предложения всё единичное выясняется стертым. Значит, мы ни при каких обстоятельствах не можем ограничиваться одним лишь значением предложения; но и идея сама по себе не образовывает познания; таковым есть идея совместно со своим значением, другими словами со своим истинностным значением. На процесс суждения возможно наблюдать как на переход от мысли к значению ее истинности.[22]
Суждения с модальностями
Модальностями (от латинского слова modus – метод) в логике именуют нюансы истинности суждения. В действительности, некое подлинное суждение А возможно действительно в любой момент либо иногда, либо на следующий день – это временная модальность, либо оно должно быть действительно, начиная с того момента, в то время, когда об этом заявило начальствующее лицо – это деонтическая модальность либо модальность долженствования, либо оно по большому счету возможно действительно либо действительно в конечном итоге либо не имеет возможности не быть не действительно по логическим обстоятельствам – в этом случае перед нами истинностные модальности. В настоящем разделе нас будут интересовать лишь истинностные модальности, то есть такие, каковые характеризуют истинность суждений словами нужно, вправду и допустимо. При построении суждения эти слова играют роль префикса:
Быть может, что любой школьник обучится умножать трёхзначные числа в уме.
Нужно, что все, кто прочёл учебник по логике до конца, сдадут зачёт.
Префиксы «допустимо» и «нужно» читаются тут как «допустимо действительно, что А» и «нужно действительно, что А». Время от времени модальность возможно выражена в языке как свойство предмета либо другого свойства, а не как черта суждения:
Вероятный итог моего опыта лучше не трогать руками.
Нужным свойством чеснока есть резкий запах.
Эти предложения, смогут быть, но, переформулированы так, дабы модальность стала явной. Следующие предложения до некоей степени синонимичны исходным:
Быть может, что итог моего опыта лучше не трогать руками.
Нужно, что чеснок имеет резкий запах.
Логические совокупности с модальностями создаются для анализа самых различных контекстов естественного языка. Кое-какие из них представлены в таблице:
| Модальность | Модализированные суждения |
| Истинностная | Нужно, что А, быть может, что А, вправду, что А. |
| Физическая (каузальная) | В силу тех либо иных (нелогических) закономерностей нужно, что А, в силу тех либо иных (нелогических) закономерностей быть может, что А. |
| Временнaя | Было так, что А, будет так, что А, всегда было так, что А, постоянно будет так, что А. |
| Эпистемическая | Субъект i знает, что А, субъект i думает (верит), что А. |
| Деонтическая | Непременно А, не запрещаеться А, не разрещаеться А. |
| Контрфактическая | Если бы было А, то было бы и В. |
| Динамическая | Всякое исполнение программы p ведет к состоянию, в котором действительно А, по крайней мере одно исполнение программы p ведет к состоянию, в котором действительно А. |
Договоримся сейчас о введении следующих обозначений:
?А – «нужно, что А»,
А – «вправду, что А»,
?А – «быть может, что А».
Применяя эти обозначения, и логические связки, мы сможем высказывать зависимости и связи между разными модализированными суждениями. Разглядим сперва пара несложных примеров:
?А – нужно, что А действительно,
?А – быть может, что А действительно,
O?А – не нужно А,
?OА – нужно, что не-А,
O?OА – не нужно, что не-А,
O?А – нереально А;
?OА – быть может, что не-А,
O?OА – не быть может, что не-А.
Вероятны кроме этого и разные итерации (отрицаний) и повторения модальностей:
??р, ???р, ?O?Oр и т. п.
Наконец, вероятны самые ращенные комбинации связок и модальностей:
(?А ? O?OА) – необходимость А эквивалентна неосуществимости не-А;
(А ? ?А) – в случае, если А действительно, то А допустимо;
(?А ? ??А) – в случае, если А быть может, то быть может, что оно допустимо;
?(А ?В) ?(?А ??В) – в случае, если нужно, что из А направляться В, то в случае, если В нужно, то и В нужно.
Представим сейчас структуру некоторых выражений естественного языка средствами модальной логики:
В случае, если быть может, что чеснок имеет приятный запах, то быть может, что его не испугаются вампиры.
(?А ? ?OВ)
В случае, если нужно, дабы все студенты имели студбилет, то из этого, быть может, направляться, что наличие билета содействует усвоению знаний.
?(?А ? В)
Быть может, что в случае, если я утрачу собственную шляпу, то она попадёт в нехорошие руки и непременно будет использован с целью достижения ненадлежащих целей, благодаря чего, быть может, будет конфискована правоохранительными органами и тогда неизбежно окончательно провалится сквозь землю в архивах.
?(А ? (В U ?С U ?(С ? (D U ?Е))))
В случае, если разглядываемое положение имеет нужный темперамент, а из него вытекает, что мы верно готовили грядки под огурцы, то это так нужно образом.
(?А ? ((А ? В) ? ?В))