Матрицы. определения и Общие понятия
Матрицей размера именуется прямоугольная таблица, содержащая чисел, складывающаяся из столбцов и строк.
Обозначение
Таблица берется или в круглые скобки, или окружается двумя параллельными вертикальными прямыми.
В случае, если матрица содержит столбцов и строк, то матрица именуется матрицей размера либо -матрицей. Размер матрицы указывается справа внизу около ее имени, или таблицы с обозначением элементов.
Элементы матрицы
Элементы матрицы обозначаются , где — номер строчка, в которой находится элемент, а — номер столбца.
Определение
Строчок матрицы именуется нулевой, в случае, если все ее элементы равны нулю. В случае, если хотя бы один из элементов строчка не равен нулю, то строчок именуется ненулевой.
Замечание. Подобное определение и для нулевого и ненулевого столбцов матрицы.
Диагонали
Определение
Основной диагональю матрицы именуется диагональ, совершённая из левого верхнего угла матрицы в правый нижний.
Побочной диагональю матрицы именуется диагональ, совершённая из левого нижнего угла матрицы в правый верхний.
Равенство матриц; сложение матриц; умножение матрицы на число; транспонирование матриц.
3.Транспонирование матрицы- переход от матрицы А к матрице А/, в столбцы и кот строки поменялись местами с сохранением порядка. Матрица А/ наз транспонированнойотносительно матрицы А. Св-ва: 1) (А/)/=А, 2) (?А/)/=?А/, 3) (А+В)/=А/+В/.4) (АВ)/=А/В/.
1. Умножение матрицы на число. Произведением матрицы А на число ? наз матрица В=?А, элементы кот bij=?aij для i=1,2,…,m; j=1,2,…,n. Неспециализированный множитель всех элементов матрицы возможно выносить за символ матрицы. Произведение матрицы А на число 0, равняется нулевой матрице. (0А=0).
2. сложение матриц. Суммой двух матриц А и В однообразного размера m?n наз матрица С=А+В, элементы кот cij=aij+bij для i=1,2,…,m; j=1,2,…,n. ( т е матрицы складываются поэлементно). В частности А+0=А.
4.Две матрицы А и В одного размера наз равными,если они совпадают поэлементно, т е aij=bij для любых i=1,2,…m; j= 1,2,…,n.
Определитель квадратной матрицы. Вырожденные и невырожденные матрицы.
В случае, если кол-во строчков= кол-ву столбцов, то такая матрица наз квадратной размером m?m(матрица порядка m). Понятие определитель приминяется лишь для квадратных матриц, detA,(А),?. Определителем кв матрицы А наз число, кот вычисляется по след правилам: 1) А=(а11) detA=а11. 2) А=(а11а12) detA=а11а22-а12а21.
(а21а22)
3) А=(а11а12а13)
(а21а22а23)
(а31а32а33)
Для 3) правилом ?(Саррюса). detA=а11а22а33+а13а21а32+а31а12а23-а31а22а13-а11а32а23-а33а21а12.
4) Определитель п-го порядка – сумме произведения элементов какой-либо строки либо столбца на их алгебраические дополнения. ?=аi1Ai1+ai2Ai2+…+ainAin. –разложение по строчку. ?=aijA1j+a2jA2j+…+anjAnj- разложение по столбцу.Аij=(-1)i+jMij- алгеброическое дополнение.
Умножение матриц.
Умножение матриц. Умножение матрицы А на матрицу В выяснено, в случае, если число столбцов матрицы А равно строчков матрицы В. Произведением матрицы А размера m?k на матрицу В размера k?какое количество наз матрица С размера m?n, любой элемент кот = сумме произведений элементов i-строки матрицы А на соответствующие элементы j-столбца матрицы В. cij=ai1b1j+ai2b2j+…+aikbik.
7.Обратная ее вычисление и матрица.
Решить совокупность линейных уравнений с квадратной матрицей коэффициентов возможно и вторым методом, применяя обратную матрицу. Наряду с этим определитель матрицы коэффициентов должен быть кроме этого отличен от нуля.
Разглядим квадратную матрицу:
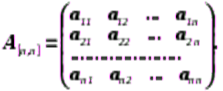
Вырожденной (особой) именуется квадратная матрица, в случае, если ее определитель равен нулю, и невырожденной (неособенной) – в другом случае.
Обратной для матрицы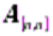 
именуется матрица 
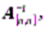в случае, если выполняется:
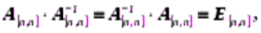
где
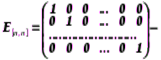единичная матрица.
Для вырожденной матрицы обратной матрицы не существует.
Обратную матрицу возможно вычислить различными методами.
А) Одно из правил вычисления обратной матрицы:
берется невырожденная матрица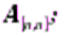 
обратная матрица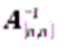 
находится по формуле
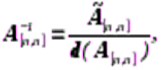
где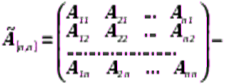 
присоединенная (либо обоюдная) матрица, складывающаяся из алгебраических дополнений 
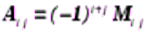элементов матрицы , где — минор порядка матрицы , приобретаемый из определителя матрицы вычеркиванием -ой строки и -ого столбца.
Обратим внимание, что в присоединенной матрице строчка транспонированы в столбцы.