Возможно выделить следующие неспециализированные группы этих задач (см. табл. 6.1).
1. Описание данных — компактное описание имеющихся данных посредством разных агрегированных (обобщенных) графиков и показателей. К этому классу возможно отнести кроме этого задачу определения нужного количества выборки[1] (предельного количества исследуемых объектов), нужного чтобы сделать обоснованные выводы.
В практике научных изучений в большинстве случаев имеется совокупность наблюдений (десятки, много, а время от времени — тысячи результатов измерений личных черт), исходя из этого появляется задача компактного описания имеющихся данных. Для этого применяют способы описательной статистики — описания результатов посредством разных агрегированных графиков и показателей. Перечислим кое-какие из них.
Для результатов измерений в шкале взаимоотношений показатели описательной статистики возможно разбить на пара групп:
— показатели положения обрисовывают положение экспериментальных данных на числовой оси. Примеры таких данных
— большой и минимальный элементы выборки, среднее значение, медиана, мода и др.;
— показатели разброса обрисовывают степень разброса данных довольно собственного центра (среднего значения). К ним относятся: выборочная дисперсия, разность между минимальным и большим элементами (размах, промежуток выборки) и др.
Таблица 6.1 – Задачи анализа экспериментальных данных
| ЗАДАЧА | Описание данных | Изучение сходства/различий | Изучение зависимостей | Понижение размерности | Классификация |
| СПОСОБЫ | — описательная статистика; — определение нужного количества выборки | Статистические параметры: Крамера-Уэлча, Вилкоксона-Манна-Уитни, c2, Фишера | — корреляционный анализ; — дисперсионный анализ; — регрессионный анализ | — факторный анализ; — способ основных компонент | — дискриминантный анализ; — кластерный анализ; — группировка |
— показатели асимметрии: положение медианы относительно среднего (величина разности их значений) и др.
— гистограмма и др.
Эти показатели употребляются для наглядного представления и первичного («визуального») анализа результатов измерений черт экспериментальной и контрольной группы.
2. Изучение сходства/различий (сравнение двух выборок). К примеру, требуется установить, точно ли различие конечных состояний экспериментальной и контрольной группы в опыте. Либо, к примеру, задача содержится в установлении совпадений либо различий черт двух выборок (к примеру, требуется установить, что средние значения доходов населения в двух регионах (либо средние значения производительности труда в двух отраслях народного хозяйства и т.д.) совпадают либо различаются). Для этого формулируются статистические догадки:
— догадка об отсутствии различий (так называемая нулевая догадка);
— догадка о значимости (достоверности) различий (так называемая другая догадка).
Для принятия ответа о том, какую из догадок (нулевую либо другую) направляться принять, применяют решающие правила — статистические критерии[2]. Другими словами, на основании информации о итогах наблюдений (чертях участников экспериментальной и контрольной группы) по известным формулам вычисляется число, именуемое эмпирическим значением критерия. Это число сравнивается с известным (к примеру, заданным таблично в соответствующих книгах по математической статистике эталонным числом, именуемым критическим значением критерия.
Критические значения приводятся, в большинстве случаев, для нескольких уровней значимости. Уровнем значимости именуется возможность неточности, заключающейся в непринятии нулевой догадки, в то время, когда она верна, другими словами возможность того, что различия сочтены значительными, а они в действительности случайны.
В большинстве случаев применяют уровни значимости (обозначаемые а), равные возможности 0,05, либо 0,01, либо 0,001. Либо, переводя в проценты, выборки не различаются с возможностями 5 %, 1 %, 0,1 %. Соответственно, возможности того, что выборки различаются составят 0,95, 0,99, 0,999, либо в процентах -95 %, 99 % и 99,9 %. В экономических, педагогических, психотерапевтических, медико-биологических экспериментальных изучениях в большинстве случаев ограничиваются значением 0,05, другими словами допускается не более чем 5 %-ая возможность неточности (95 % уровень достоверности различий). В естественных, технических науках чаще требуются уровни достоверности различий 99 % либо 99,9 %.
В случае, если полученное исследователем эмпирическое значение критерия выясняется меньше либо равняется критическому, то принимается нулевая догадка — считается, что на заданном уровне значимости (другими словами при том значении а, для которого вычислено критическое значение критерия) чёрта экспериментальной и контрольной групп совпадают. В противном случае, если эмпирическое значение критерия выясняется строго больше критического, то нулевая догадка отвергается и принимается другая догадка — чёрта экспериментальной и контрольной группы считаются разными с достоверностью различий 1 — а. К примеру, в случае, если а = 0,05 и принята другая догадка, то достоверность различий равна 0,95 либо 95%.
Иначе говоря чем меньше эмпирическое значение критерия (чем левее оно находится от критического значения), тем больше степень совпадения черт сравниваемых объектов. И напротив, чем больше эмпирическое значение критерия (чем правее оно находится от критического значения), тем посильнее различаются характеристики сравниваемых объектов.
Итак, в случае, если мы ограничимся уровнем значимости a = 0,05, то, в случае, если эмпирическое значение критерия оказывается меньше либо равняется критическому, то возможно сделать вывод, что «характеристики экспериментальной и контрольной групп совпадают на уровне значимости 0,05». В случае, если эмпирическое значение критерия выясняется строго больше критического, то возможно сделать вывод, что «достоверность различий черт экспериментальной и контрольной групп равна 95 %».
Приведем метод выбора статистического критерия (см. табл. 6.2). Во-первых, нужно выяснить, какая
Таблица 6.2 – Метод выбора статистического критерия
| Шкала | Статистический критерий |
| измерений | |
| Взаимоотношений | Крамера-Уэлча, Вилкоксона-Манна-Уитни |
| Порядковая | Вилкоксона-Манна-Уитни, c2 |
| Номинальная | c2 |
| Дихотомическая | Фишера |
шкала измерений употребляется — взаимоотношений, порядковая либо номинальная.
Для шкалы взаимоотношений целесообразно применять критерий Крамера-Уэлча. В случае, если число различающихся между собой значений[3] в сравниваемых выборках громадно (более десяти)[4], то допустимо применение критерия Вилкоксона- Манна-Уитни.
Для порядковой шкалы целесообразно применять критерий Вилкоксона-Манна-Уитни, допустимо кроме этого применение критерия c2.
Для номинальной шкалы направляться применять критерий c2.
Для дихотомической шкалы (номинальной шкалы с двумя вероятными значениями) направляться применять критерий Фишера.
3. Изучение зависимостей. Следующим шагом по окончании изучения сходства/различий есть установление факта наличия/отсутствия зависимости между показателями и количественное описание этих зависимостей. Для этих целей употребляются, соответственно, корреляционный и дисперсионный анализ, и регрессионный анализ.
Корреляционный анализ. Корреляция (correlation) — связь между двумя либо более переменными (в последнем случае корреляция именуется множественной). Цель корреляционного анализа — установление наличия либо отсутствия данной связи, другими словами установление факта зависимости каких-либо явлений, процессов друг от друга либо их независимости.
При, в то время, когда имеются две переменные, значения которых измерены в шкале отношений[5], употребляется коэффициент линейной корреляции Пирсона r, что принимает значения от -1 до +1 (нулевое его значение говорит об отсутствии корреляции[6]) — см. Рис. 6.1, на котором любая точка соответствует отдельному объекту, обрисовываемому двумя переменным — х и у. Термин «линейный» говорит о том, что исследуется наличие линейной связи между переменными — в случае, если r(х, у) = 1, то одна переменная линейно зависит от второй (и, конечно, напротив), другими словами существуют константы а и b, причем, а 0, такие что у = а х + b.
На рис. 6.1, а и в изображены ситуации, в то время, когда все экспериментальные точки лежат на прямой (полное значение коэффициента линейной корреляции равняется единице). В ситуации, изображенной на рис. 6.1, б, конкретно совершить прямую через экспериментальные точки нереально (коэффициент линейной корреляции равен нулю).
В случае, если экспериментальные точки сгруппированы около некоей прямой — см. рис. 6.1, г и д, то коэффициент линейной корреляции принимает значения, хорошие от нуля, причем чем «ближе» точки к прямой, тем выше безотносительное значение коэффициента линейной корреляции. Другими словами, чем выше безотносительное значение коэффициента Пирсона, тем посильнее исследуемые переменные линейно связаны между собой.
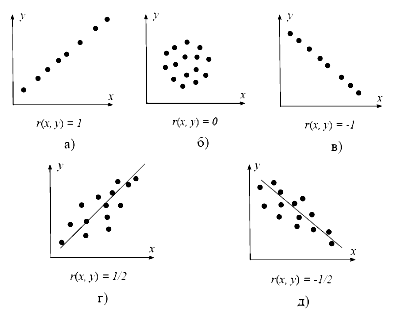
Рисунок 6.1 – Величины коэффициента линейной корреляции в разных обстановках
Для данных, измеренных в порядковой шкале, направляться применять коэффициент ранговой корреляции Спирмена (он может использоваться и для данных, измеренных в интервальной шкале, поскольку есть непараметрическим и улавливает тенденцию — трансформации переменных в одном направлении), что обозначается s и определяется сравнением рангов — номеров значений сравниваемых переменных в их упорядочении.
Коэффициент корреляции Спирмена есть менее чувствительным, чем коэффициент корреляции Пирсона (так как первый при измерений в шкале взаимоотношений учитывает только упорядочение элементов выборки). Одновременно с этим, он разрешает выявлять корреляцию между монотонно нелинейно связанными переменными (для которых коэффициент Пирсона может показывать малого корреляцию.
Напомним, что громадное (близкое к плюс единице либо к минус единице) значение коэффициента корреляции говорит о связи переменных, но ничего не может сказать о причинно- следственных отношениях между ними. Так, к примеру, из большой корреляции температуры воздуха за окном и времени дней нельзя делать вывод о том, что перемещение солнца обусловлено трансформациями температуры воздуха. Исходя из этого для установления обстоятельств связей между какими-либо явлениями, процессами нужны дополнительные изучения по содержательной интерпретации этих связей.
Дисперсионный анализ. Изучение наличия либо отсутствия зависимости между переменными возможно кроме этого проводить и посредством дисперсионного анализа. Его сущность содержится в следующем. Дисперсия характеризует «разброс» значений переменной. Переменные связаны, в случае, если для объектов, отличающихся значениями одной переменной, отличаются и значения второй переменной. Значит, необходимо для всех объектов, имеющих одно да и то же значение одной переменной (именуемой свободной переменной), взглянуть, как различаются (как велика дисперсия) значения второй (или других) переменной, именуемой зависимой переменной. Дисперсионный анализ именно и позволяет сравнить отношение дисперсии зависимой переменной (межгрупповой дисперсии) с дисперсией в групп объектов, характеризуемых одними и теми же значениями свободной переменной (внутригрупповой дисперсией).
Иначе говоря дисперсионный анализ «трудится» следующим образом. Выдвигается догадка о наличии зависимости между переменными: к примеру, между уровнем образования и возрастом сотрудников некоей организации. Выделяются группы элементов выборки (сотрудников) с однообразными значениями свободной переменной — возраста, другими словами сотрудников одного возраста (либо принадлежащих выделенному возрастному диапазону). В случае, если догадка о зависимости уровня образования от возраста верна, то значения зависимой переменной (уровня образования) в каждой таковой группы должны различаться не сильно (в- групповая дисперсия уровня образования должна быть мелка). Наоборот, значения зависимой переменной для различающихся по возрасту групп сотрудников должны различаться очень сильно (межгрупповая дисперсия уровня образования должна быть громадна). Другими словами, переменные зависимы, в случае, если отношение межгрупповой дисперсии к внутригрупповой громадно. В случае, если же догадка о наличии зависимости между переменными не верна, то это отношение должно быть мало.
Регрессионный анализ. В случае, если корреляционный и дисперсионный анализ дают ответ на вопрос, существует ли связь между переменными, то регрессионный анализ рекомендован чтобы отыскать «явный вид» функциональной зависимости между переменными. Для этого предполагается, что зависимая переменная (время от времени именуемая откликом) определяется известной функцией (время от времени говорят — моделью), зависящей от зависимой переменной либо переменных (время от времени именуемых факторами) и некоего параметра. Требуется отыскать такие значения этого параметра, дабы полученная зависимость (модель) наилучшим образом обрисовывала имеющиеся экспериментальные эти. К примеру, в простой[7] линейной регрессии предполагается, что зависимая переменная у есть линейной функцией у = а х + b от свободной переменной х. Требуется определить значения параметров а и b, при которых прямая а х + Ъ будет наилучшим образом обрисовывать (аппроксимировать) экспериментальные точки (х1, у1), (х2, у2), …, (хn, уn).
Возможно применять полиномиальную регрессию, в которой предполагается, что зависимая переменная есть полиномом (многочленом) некоей степени от свободной переменной (отметим, что линейная зависимость есть полиномом первой степени). К примеру, полиномом второй степени (знакомая всем из школьного курса алгебры парабола) будет зависимость вида у = а х2 + b х + с и задачей регрессии будет нахождение коэффициентов а, b и с.
Выше мы разглядели несложную регрессию (по одной свободной переменной) — линейную и нелинейную. Допустимо кроме этого применение множественной регрессии — определения зависимости одной переменной от нескольких факторов (свободных переменных).
Регрессионный анализ, кроме того, что он разрешает количественно обрисовывать зависимость между переменными, позволяет прогнозировать значения зависимых переменных — подставляя в отысканную формулу значения свободных переменных, возможно приобретать прогноз значений зависимых. Наряду с этим направляться не забывать, что выстроенная модель «локальна», другими словами, взята для некоторых в полной мере конкретных значений переменных. Экстраполяция результатов модели на более широкие области значений переменных может привести к ошибочным выводам.
4. Понижение размерности. Довольно часто в следствии экспериментальных изучений появляются громадные массивы информации. К примеру, в случае, если любой из исследуемых объектов описывается по нескольким параметрам (измеряются значения нескольких переменных — показателей), то результатом измерений будет таблица с числом ячеек, равным произведению числа объектов на число показателей (показателей, черт). Появляется вопрос, а все ли переменные являются ин формативными. Само собой разумеется, исследователю нужно было бы распознать значительные переменные (это принципиально важно с содержательной точки зрения) и сконцентрировать внимание на них. Помимо этого, в любой момент нужно уменьшать количества обрабатываемой информации (не теряя наряду с этим сути). Чем тут смогут оказать помощь статистические способы?
Существует целый класс задач понижения размерности, цель которых именно и содержится в уменьшении числа разбираемых переменных или при помощи выделения значительных переменных, или/и построения новых показателей (на основании взятых в следствии опыта).
Для понижения размерности употребляется факторный анализ, а главными способами являются коротко разглядываемый ниже способ основных компонент и многомерное шкалирование.
Способ основных компонент содержится в получении нескольких новых показателей — основных компонент, являющихся линейными комбинациями исходных показателей (отметим, что линейной комбинацией именуется взвешенная сумма), взятых в следствии опыта. Главные компоненты упорядочиваются в порядке убывания той дисперсии, которую они «растолковывают». Первая основная компонента растолковывает солидную часть дисперсии, чем вторая, вторая — громадную, чем третья и т.д. Ясно, что чем больше основных компонент будет учитываться, тем солидную часть трансформаций возможно будет растолковать.
Преимущество способа основных компонент содержится в том, что обычно первые пара основных компонент (одна-две-три) растолковывают солидную часть (к примеру, 80-90 %) трансформаций солидного числа (десятков, а время от времени и сотен) показателей. Помимо этого, может оказаться, что в первые пара основных компонент входят не все исходные параметры. Тогда возможно сделать вывод о том, какие конкретно параметры являются значительными, и на них направляться обратить внимание первым делом.
Решив задачи описания данных, установления сходства/отличий, проанализировав как следует и количественно зависимости между переменными и распознав значительные переменные, возможно разбирать соотношение групп переменных и пробовать прогнозировать значения одних переменных в зависимости от значений вторых переменных либо времени развития того либо иного процесса.
5. Классификация. Широкую группу задач анализа данных, основывающихся на применении статистических способов, составляют так именуемые задачи классификации. В родных смыслах (в зависимости от предметной области) употребляются кроме этого термины: «группировка», «систематизация», «таксономия», «диагностика», «прогноз», «принятие ответов», «распознавание образов». Обсудим кое-какие различия между этими терминами. Предложено выделить три подобласти теории классификации: дискриминация (дискриминантный анализ), кластеризация (кластерный анализ) и группировка. Тут мы коротко остановимся на сути этих способов.
В дискриминантном анализе классы предполагаются заданными (к примеру, обучающими выборками, для элементов которых известно, каким классам они принадлежат: к примеру, больной-здоровый, правильно-неправильно, легкая степень заболевания — средняя — тяжелая и т.д.). Задача содержится в том, дабы любой снова появляющийся объект отнести к одному из этих классов. У термина «дискриминация» имеется множество синонимов: диагностика (к примеру, в медицине требуется поставить диагноз из конечного перечня вероятных заключений, в случае, если известны определенные характеристики больного и известно, какие конкретно заключения ставились больным, вошедшим в обучающую выборку), распознавание образов с преподавателем, автоматическая (либо статистическая) классификация с преподавателем и т.д.
В случае, если в дискриминантном анализе классы заданы, то группировка и кластеризация предназначены для выделения и выявления классов. Синонимами являются: построение классификации, таксономия, распознавание образов без преподавателя, автоматическая классификация без преподавателя и т. д.
Задача кластерного анализа содержится в выделении по эмпирическим данным быстро различающихся групп (кластеров) объектов, каковые схожи между собой в каждой из групп.
При группировке, в то время, когда резких границ между кластерами не существует, исследователю приходится самому вводить границы между группами объектов.
Применение компьютера при анализе результатов опыта, без сомнений, целесообразно. С одной стороны, последовательность статистических способов реализован в таковой популярной программе, как Микрософт Excel для Windows, входящей в обычный набор Микрософт Office, и установленной на любом современном компьютере. Иначе, на сегодня существует множество особых опытных программ, разрешающих осуществлять статистический анализ данных. Среди последних возможно выделить и советовать к применению такие самый распространенные пакеты статистического анализа как: Statistice, StatGraphics и SPSS. Но, упомянутые программы достаточно сложны и требуют больших временных затрат для их освоения. Исходя из этого возможно советовать следующее: в случае, если для ответа задач изучения достаточно возможностей Ехсе1, то возможно ограничиться применением данной программы (недочётом ее, действительно, есть фактически полное отсутствие вразумительных объяснений, каковые помогли бы неподготовленному пользователю осознать, что оказалось в следствии расчетов). В случае, если возможностей Ехсеl слишком мало, то необходимо обращаться к опытным статистическим программам. Любая из них владеет недостатками и своими достоинствами (в одной более полно реализованы одни способы, в второй другие и т.д.). С методической точки зрения возможно советовать применять программу StatGraphics (версии 5.0 и выше). Ее преимуществом с позиций неумелого статистика есть наличие «советчика», что разъясняет, что свидетельствует та либо другая вычисленная величина, и что исследователю направляться делать дальше.
Завершив описание статистических способов, напомним, что довольно часто при организации изучения сложных процессов и явлений и обработке его результатов появляется необходимость применения агрегированных (комплексных) и/либо векторных оценок. Разглядим коротко их специфику.
Агрегированные оценки. Во многих опытах имеется большое число (десятки, много, а время от времени и тысячи) объектов (субъектов). В следствии измерения их показателей получается комплект их частных оценок. Ясно, что сравнивать между собой и разбирать в один момент все частные оценки не всегда допустимо и целесообразно, поскольку постоянно существует их разброс, обусловленный неконтролируемым различием объектов опыта.
Исходя из этого чтобы, во-первых, взять обозримое число черт и, во-вторых, чтобы сгладить личные колебания, применяют так именуемые агрегированные (коллективные, групповые, производные) оценки. К примеру, в случае, если имелись частные (личные) оценки отдельных индивидуумов, то агрегированной оценкой будет «среднее» значение для их группы. Применение кавычек не просто так, поскольку получение агрегированных оценок на основании частных есть их преобразованием, и преобразование это направляться делать корректно.
Приведем кое-какие корректные процедуры агрегирования для самый распространенных в экспериментальных изучениях показателей.
Для размеров, измеренных в шкале взаимоотношений, самоё типичным есть вычисление среднего арифметического по группе. Эта процедура в полной мере корректна, и в большинстве случаев ее реализация не вызывает затруднений.
Наибольшее число неточностей появляется при агрегировании показателей, измеренных в порядковых шкалах. Напомним, что не нужно складывать, вычитать, умножать либо дробить баллы друг на друга, да и на дабы то ни было — все это полностью тщетные операции. В порядковой шкале для «сглаживания» в большинстве случаев применяют медиану.
В случае, если имеется комплект личных баллов, то агрегированной чёртом группы будет число ее участников, взявших тот либо другой балл[8]. Подобным образом агрегируется и информация о выделении уровней — в случае, если введены три уровня (к примеру, уровни знаний: низкий, средний и большой) и имеется информация о распределении всех участников нескольких групп (контрольных либо экспериментальных) по этим уровням, то агрегированной информацией об объединенной группе будет число ее участников, владеющих тем либо иным уровнем (вычисляемое как сумма по всем группам числа их участников, владеющих данным уровнем).
В случае, если агрегирование частных оценок по группе экспериментальных объектов (субъектов) производится с целью получения черт группы в целом, то для описания разных качеств, особенностей и т.п. одного и того же объекта употребляются так именуемые векторные оценки.
Векторные оценки. Часто видятся случаи, в то время, когда какое-либо изучаемое явление, процесс характеризуется несколькими показателями — вектором показателей. К примеру, при оценке труда какого-нибудь рабочего употребляются показатели качества труда (точности обработки подробностей) и производительности труда (время исполнения операций). Наряду с этим довольно часто появляется вопрос о возможности однозначной оценки этого явления, процесса либо изучаемых их особенностей одной величиной — комплексной оценкой. К примеру, во многих спортивных состязаниях победитель выявляется по комплексной оценке — сумме очков, баллов, собранных на отдельных этапах состязания либо в отдельных играх, в многоборье — в отдельных видах спорта.
На практике комплексные оценки видятся частенько и, разумеется, без них не обойтись, не смотря на то, что методы их определения часто и приводят к множеству недоуменных вопросов. Но в любом случае такие комплексные оценки, используемые в повседневной судьбе, являются или результатом определенных публичных соглашений, каковые будут считаться всеми участниками, или установлены каким- или нормативным актом определенного директивного органа — министерства, ведомства и т.д. и поэтому кроме этого будут считаться всеми заинтересованными лицами.
Другое дело — использование комплексных оценок в научном изучении. Тут сходу на первое место поднимается вопрос о научной, а также математической, строгости используемой оценки. В частности, к примеру, не вызывает сомнений возможность применения в организации труда таковой комплексной оценки, как суммарные затраты времени на исполнение тех либо иных технологических операций. Тут суммируются однородные размеры, измеренные в шкале взаимоотношений.
В это же время, при применении шкалы рангов (порядковой шкалы) суммирование баллов частенько видится в изучениях по педагогике, психологии, медицине, биологии и вторым наукам. Так, в одной «методологической» публикации для оценки эффективности рабочий игры была использована следующая «формула»: Р = 50 — К — (В — 40), где Р — «комплексная» оценка в баллах, 50 — предельное число баллов, К — количество замечаний, сделанных ведущим, В — время в минутах. Как видим, тут уж, что именуется, «смешались в кучу кони, люди …». Под символ суммы (разности) поставлены совсем разнородные размеры: баллы, количество замечаний, время, безразмерные числа.
Достаточно несложным и интуитивно понятным (но, одновременно с этим, корректным) способом агрегирования балльных оценок есть применение так называемых матриц свертки, элементы которых содержат значения агрегированного показателя, а агрегируемые баллы задают номер столбца и строки.
В некое оправдание применяемым на практике некорректным построениям комплексных оценок направляться подчернуть, что неприятность агрегирования векторных оценок на сегодня изучена не абсолютно, а существующие результаты, кроме того для их применения на практике, обычно требуют хорошего знания высшей математики. как следует же неприятность векторных оценок (либо как ее время от времени именуют — неприятность принятия ответов при многих параметрах) возможно проиллюстрирована на следующем несложном примере из области экономики: имеются два инвестиционных проекта с одним и тем же размером начальных вложений (допустим, 100 единиц), причем первый характеризуется более высоким доходом (300 единиц), но и более высоким риском (предположим, что возможность неуспеха равна 0,2), чем второй (доход — 250 единиц, возможность неуспеха (риск) — 0,05). В какой из проектов направляться осуществлять инвестиции?
Ответ неоднозначен. Если бы первый проект был более прибыльным и менее рискованным, то следовало бы выбирать его. Но имеются два критерия (риск и доход) и первая альтернатива (первый проект) «лучше» по одному критерию, но «хуже» по второму. В аналогичных обстановках в большинстве случаев поступают следующим образом. На первом шаге выделяют множество действенных альтернатив (так называемых, недоминируемых по Парето, другими словами таких альтернатив, что не существует вторых допустимых альтернатив, каковые были бы «не хуже» по всем параметрам, а по одному из параметров — «строго лучше»). В разглядываемом примере оба проекта действенны по Парето.
Дальше — на втором шаге — допустимо пара вариантов (и привести a priori рациональное обоснование того, какой из них направляться применять в том либо другом конкретном случае, нереально):
— ввести комплексный критерий, оценка по которому будет вычисляться агрегированием оценок по исходным параметрам. В разглядываемом примере таким критерием возможно ожидаемый доход (произведение дохода на возможность его получения). Значение для того чтобы комплексного критерия для первого проекта равняется 240 = 300 (1 — 0,2), для второго — 237,5 = =250 (1 — 0,05). С позиций максимизации ожидаемого дохода направляться выбрать первый проект. В качестве комплексного критерия возможно применять ожидаемые утраты (для первого проекта они равны 60 единиц, для второго — 12,5), тогда с позиций минимизации ожидаемых утрат направляться выбрать второй проект;
— упорядочить критерии по важности. В случае, если вычислять доход более ответственным критерием, чем риск, то направляться выбрать первый проект (так как он приносит при успехе больший доход: 300 250). Но, в случае, если вычислять риск более серьёзным критерием, чем доход, то направляться выбрать второй проект (так как он характеризуется меньшим риском: 0,05 0,2);
— вероятны и другие варианты принятия ответов, часть из которых будет «советовать» выбрать первый проект, а вторая часть — второй.
Кроме того из приведенного элементарного примера многокритериальной задачи принятия ответов видно, что универсальных «рецептов» в данной области не существует. Но в любом случае при построении комплексных оценок необходимо быть предельно внимательным и осмотрительным. Кстати, часто возможно обойтись и без них. В случае, если взяты количественные результаты по отдельным показателям, то возможно ограничиться их качественной интерпретацией, не «загоняя под неспециализированный знаменатель», проанализировать и сравнить исследуемые объекты раздельно по каждому из показателей. И пускай по каким-то показателям результаты экспериментальных групп будут лучше контрольных, а по каким-то хуже – от этого изучение лишь обогатится, станет точнее.
Контрольные вопросы
1. Перечислите задачи анализа экспериментальных данных.
2. Способы описательной статистики.
3. Приведите метод выбора статистического критерия.
4. Корреляционный анализ.
5. Дисперсионный анализ.
6. Регрессионный анализ.
7. Применение компьютера при анализе результатов опыта.
Рекомендуемая литература
1. Новиков А. М. Методика научного изучения / А. М. Новиков, Д. А. Новиков. – М. : Либроком, 2010. – 280 с.
2. Лукашевич В. К. Базы методики научных изучений : Учеб. пособие для студентов институтов / В. К. Лукашевич. – Мн. : ООО «Элайда», 2001. – 104 с.
3. Сабитов Р. А. Базы научных изучений : Учеб. пособие для институтов / Р. А. Сабитов. – Челябинск : Челябинский национальный университет, 2002. – 138 с.
4. Макогон Ю. В. Методика научных изучений внешнеэкономических связей / Ю. В. Макогон, В.В. Пилипенко. – Донецк : ДНУ, 2002. – 170 с.
5. Баскаков А. Я. Методика научного изучения : Учеб. пособие для институтов / А. Я. Баскаков, Н. В. Туленков. – К. : МАУП, 2004. – 216 с.
6. Новиков А. М. Методика / А. М. Новиков, Д. А. Новиков. – М. : СИНТЕГ, 2007. – 668 с.
7. Бургин М. С. Введение в современную правильную методику науки: структуры совокупностей знания: Пособие для студентов институтов / М. С. Бургин, В. И. Кузнецов. – М. : АО «Нюанс Пресс», 1994. – 304 с.