Цель транспортной задачи — разработка наиболее способов транспортировки и рациональных путей товаров, устранение чрезмерно дальних, повторных перевозок и встречных.
Обозначения:
m – количество пунктов отправления (поставщиков);
i – номер поставщика;
n – количество пунктов назначения (потребителей);
j – номер потребителя;
ai – количество однородного груза i-го поставщика (запасы);
bi – количество однородного груза, требуемого j-ому потребителю (спрос);
cij – цена доставки единицы груза i-го поставщика j-ому потребителю;
xij – количество груза, доставляемое от i-го поставщика к j-му потребителю;
С – неспециализированные затраты на перевозки.
Пускай в пунктах (поставщиках) сосредоточен однородный груз (сено, картофель и т.д.) в количествах соответственно , что нужно перевезти потребителям в количествах . Известны транспортные затраты (тарифы) , по перевозке единицы груза от поставщика к потребителю . Требуется разработать замысел перевозки груза, по которому:
1) груз от каждого поставщика должен быть вывезен;
2) спрос каждого потребителя абсолютно удовлетворен;
3) затраты на перевозку должны быть минимальными.
Нужное и достаточное условие ответа поставленной задачи пребывает в том, дабы суммарный запас груза был бы равен суммарному спросу на него, другими словами . В случае, если это условие выполнено, то соответствующая ТЗ носит название задачи с закрытой моделью.
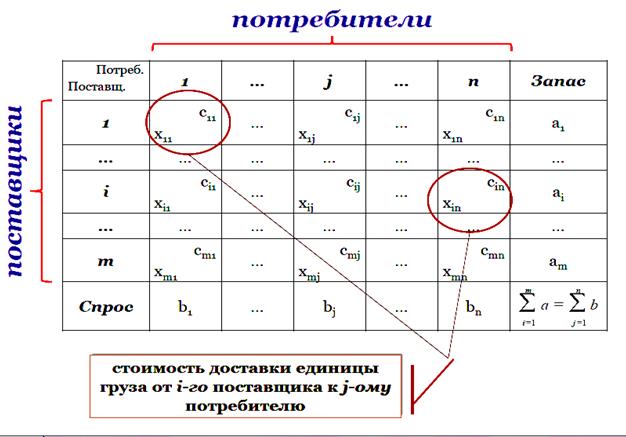
Условия транспортной задачи возможно записать в виде распределительной таблицы 1, где указаны запасы и поставщики груза у них , их потребность и потребители в грузе , цена перевозок единицы груза , из пункта в пункт . Таблица 1
| Поставщик | Потребители | Запас груза | ||
| …………… | ||||
| …………… | ||||
| …………… | …………… | …………… | …………… | …………… |
| …………… | ||||
| Потребность в грузе | …………… | 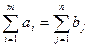
|
В клетках данной же распределительной таблицы возможно разработать замысел перевозок груза из пункта в пункт . Наряду с этим затраты на перевозку груза составят:
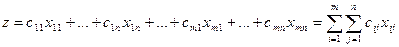 (1)
(1)
Так, математическая формулировка ТЗ следующая: Отыскать , в случае, если переменные удовлетворяют условиям:
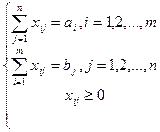 (2)
(2)
Совокупность ограничений (2) складывается из уравнений, в которых содержится переменных. В теории ТЗ доказывается, что ранг матрицы совокупности (2) равен и исходя из этого опорный замысел ответа задачи содержит базовых переменных, остальные переменные являются свободными и в опорном замысле принимают значения равные нулю.
2. Этапы определения замысла ответа транспортной задачи.
При составлении опорного замысла ответа задачи в распределительной таблице 1 будут заполнены не более клеток, остальные клетки будут свободными (безлюдными), так как соответствующий им груз равен нулю.
Так, замысел ответа ТЗ возможно выяснен следующими этапами:
1. Построение опорного замысла ответа ТЗ (в распределительной таблице заполняются не более клеток).
2. Проверка опорного замысла на оптимальность.
3. Улучшение опорного замысла, если он не оптимальный.
4. Проверка улучшенного замысла на оптимальность. Процесс заканчивается оптимальным замыслом.
Разглядим любой этап ответа ТЗ.
1. Построение опорного замысла ответа ТЗ.
Разглядим два способа построения опорного замысла.
а) Способ «Северо-западного угла»
Сущность этого способа пребывает в том, что заполнение распределительной таблицы ТЗ начинается с левого верхнего угла (клетка 1;1). В ней записывается максимальный груз: . К примеру, в случае, если , то и груз из пункта вывезен в пункт , но в нужно завозить еще единицу груза. Данный недостающий груз завозим из пункта , записывая в клетку (2;1) максимальный груз . Заполнив клетку (2;1), заполняем следующую, или в той же строке 2 (в случае, если ), или в строчке 3 (в случае, если ). Последней заполняется клетка . Наряду с этим число заполненных клеток будет не более .Пример построения опорного замысла способом «Северо-западного угла» приведен для следующей задачи .
Задача №1.
Компания, производящая газированные напитки, складируемые в трех различных местах, обязана поставить продукцию в четыре супермаркета. Любая упаковка содержит 20 бутылок по 1,5 литра, тарифы на доставку товара, заказы и объёмы запасов на продукцию приведены в табл. 2.
Таблица 2.Результаты расчетов.
| Поставщики | Потребители | Запасы груза | |||
| Потребность в грузе |
Затраты на перевозку 300 ед. груза согласно этому плану составляют:
(у.е.)
б) Способ «Минимального элемента»
Опорный замысел, выстроенный по способу «Северо-западного угла» в большинстве случаев оказывается далеким от оптимального, поскольку при его составлении игнорируются величины затрат . Исходя из этого существуют другие способы составления начального опорного замысла. Несложный из них — способ «Минимального элемента». В отличие от способа «Северо-западного угла», тут заполнение распределительной таблицы начинается из клетки, у которой мельчайший тариф. В эту клетку заносится максимальный груз. Наряду с этим или строчок, или столбец окажутся заполненными. Потом заполняется следующая клетка (строчка либо столбцы), имеющая мельчайший тариф.
Пример построения опорного замысла способом «Минимального элемента» приведен в табл. 3.
Таблица 3.Результаты расчетов.
| Поставщики | Потребители | Запасы груза | |||
| Потребность в грузе |
Тут порядок заполнения клеток следующий:
.
Затраты по этому маршруту перевозок составят: (у.е.). Мы видим, что согласно этому плану затраты на перевозку груза намного меньше . И в таблице 2 и в таблице 3 заполненных клеток выяснилось 3 + 4 — 1 = 6.
2. Проверка опорного замысла на оптимальность.
Будем контролировать опорный замысел на оптимальность способом потенциалов. Сущность его пребывает в том, что каждой столбцу и строке распределительной таблицы приписываются кое-какие числа именуемые потенциалами. Так, числа — потенциалы строчков, — потенциалы столбцов. Эти числа рассчитываются по формуле: для каждой заполненной клеткираспределительной таблицы сумма столбца и потенциалов строки равна тарифу соответствующей заполненной клетки, другими словами
. (3)
Так как заполненных клеток не более , а число всех столбцов и потенциалов строк равна , то в совокупности уравнений (3) имеется уравнений с малоизвестными и она имеет вечно довольно много ответов. В этом случае одной из малоизвестных возможно дать определенное значение и тогда совокупность будет иметь единственное ответ. В большинстве случаев потенциал первой строчки вычисляют равным нулю ( ) и потом по этому потенциалу и по заполненным клеткам первой строчки находят потенциалы соответствующих столбцов, а по заполненным клеткам столбцов, находят потенциалы вторых строчков.
Вычислив, так, потенциалы столбцов и строк, вычисляем характеристики свободных клеток распределительной таблицы по формуле: . Отрицательные характеристики каких-то свободных клеток показывают на их перспективность: в этих клетках тарифы мелки и их заполнение приведет к улучшению замысла перевозок. Итак, в случае, если хотя бы одна свободная клетка будет иметь отрицательную чёрта, то замысел есть не оптимальным и его нужно улучшать.
Замечание. Методика столбцов потенциалов и вычисления строк значительным образом опирается на то, что заполнено ровно клеток. В случае, если заполненных клеток будет меньше, чем (таковой замысел именуется вырожденным), то при расчете потенциалов в нужное количество безлюдных клеток записывают нуль груза и вычисляют их заполненными.
3. Метод улучшения неоптимального замысла.
Переход к лучшему замыслу осуществляется посредством заполнения клетки и перераспределения груза с отрицательной чёртом. В случае, если таких клеток пара, то выбирают ту, в которой отрицательная черта была самой большой по полной величине. Перераспределение груза происходит по замкнутому маршруту (контуру), что строится по следующей схеме:
1) Маршрут начинается и заканчивается в клетке с отрицательной чёртом;
2) Линии контура строго вертикальны либо горизонтальны (нельзя двигаться по диагонали);
3) Повороты (на 900) возможно осуществлять лишь в заполненных клетках.
По окончании построения замкнутого маршрута (самый несложный вариант – прямоугольник), происходит перераспределение груза (улучшение опорного замысла) по следующей схеме:
4) Каждой угловой клетке маршрута (где осуществлялись повороты на 900) присваивается символ «+» либо «-», причем клетке, из которой начинается маршрут, приписывают символ «+», потом символы чередуются;
5) Среди клеток со знаком «-» выбирают клетку с мельчайшим грузом;
6) Мельчайший груз прибавляют ко всем клеткам со знаком «+» и вычитают из всех клеток со знаком «-». Наряду с этим безлюдная клетка, из которой начиналось перемещение и которая имела отрицательную чёрта, делается заполненной, а заполненная клетка, имевшая груз, что подлежал перераспределению, стала безлюдной.
Потом, улучшенный замысел снова контролируют на оптимальность и улучшают , пока характеристики всех безлюдных клеток не окажутся хорошими. Это указывает, что безлюдными были клетки с громадными тарифами, а заполнены клетки с малыми тарифами и исходя из этого затраты на перевозку груза были минимальными.
Удостоверимся в надежности, к примеру, оптимальность замысла, выстроенного способом «Минимального элемента» в таблице 3 (он лучше замысла выстроенного способом «Северо-западного угла» в таблице 2). Для этого вычислим потенциалы столбцов и строк по заполненным клеткам табл. 3. Результаты расчетов запишем в таблицу 4
Таблица 4.Результаты расчетов.
| Поставщики | Потребители | Потенциалы строчков | |||
| «-» 7 | «+» 5 | ||||
| «-» 1 | 75 «+» | — 5 | |||
| «+» | 50 «-» | — 3 | |||
| Потенциалы столбцов |
Сейчас по таблице 4 вычислим характеристики свободных клеток. Имеем, ; ; ; ; ; (-3+3)=20.Так, среди свободных клеток одна клетка (3;1) имеет отрицательную чёрта .
По обрисованной выше схеме строим маршрут перераспределения груза. Перемещение начинаем из клетки (3;1) и ей присваиваем символ «+». Потом символы чередуются. Среди клеток со знаком «-» мельчайший груз (равный 5 ед.) в клетке (1;2). Данный груз мы вычитаем из клеток (1;2), (2;1), (3;4) и прибавляем в клетки со знаком «+» (3;1), (1;4), (2;2).
Таблица 5.Результаты расчетов.
| Поставщики | Потребители | Запасы груза | |||
| Потребность в грузе |
Приобретаем новый опорный замысел (таблица 5).
Затраты по новому замыслу составят (у.е.). Проверка этого замысла говорит о том, что он оптимальный.
Замечание. В случае, если в опорном замысле выяснилось пара клеток с отрицательной чёртом, то маршрут перераспределения начинается из клетки с самой большой по безотносительной величине отрицательной чёртом.
Лекция № 12
Тема: Открытая транспортная задача
Замысел:
1. Математическая формулировка открытой транспортной задачи.
2. Введение фиктивного поставщика (потребителя) для сведения данной транспортной модели к ЗТЗ.