Среди форм применяемых нами блоков (либо фигур) не считая треугольника, квадрата, прямоугольника имеется и круг. Помимо этого, многие предметы, с которыми видятся дети (тарелки, блюдца, колеса велосипеда и др.), имеют круглую форму. Вычисляем нецелесообразным для дошкольников вводить термин окружность.
В элементарной геометрии круг определяется как множество (либо геометрическое место) всех точек плоскости, удаленных от некоей точки, именуемой центром, на расстояние, не превышающее R (R — радиус круга); окружность определяется подобно как множество всех точек плоскости, удаленных от точки, именуемой центром, на одно да и то же расстояние R.
Увидим, что в случае, если в этих формулировках слово «плоскость» заменить словом «пространство», то окажутся сферы и определения шара, соответственно, пространственных аналогов окружности и круга.
Круг, окружность, шар и сферу возможно выяснить и генетически, т. е. описанием процесса образования этих фигур. Данный процесс легко смоделировать: в случае, если отрезок зафиксировать в одном финише и вращать его около этого финиша, то он обрисует круг, а второй его финиш — окружность. В случае, если полукруг вращать около диаметра, то он обрисует шар, а ограничивающая его полуокружность — сферу.
Дошкольники знакомятся кроме этого с одним из несложных многогранников, каким есть куб.
Куб — пространственный аналог квадрата. Он ограничен шестью квадратами. Его возможно сконструировать (склеить) из плоской фигуры — выкройки, изображенной на илл. 15
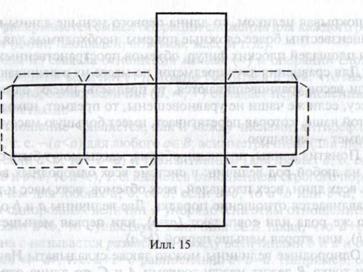
Ознакомление детей с обрисованными выше несложными фигурами есть пропедевтической базой для развития и дальнейшего формирования у них геометрических, а также пространственных, представлений.
2.5. Величины и их измерение
Что такое величина
Величина — одно из главных математических понятий, появившееся в древности и подвергшееся в ходе долгого развития последовательности обобщений.
Неспециализированное понятие величины есть ярким обобщением более конкретных понятий: длины, площади, количества, массы, скорости и т. п. Любой конкретный род размеров связан с определенным методом сравнения соответствующих особенностей объектов. К примеру, в геометрии отрезки сравниваются при помощи наложения, и это сравнение ведет к понятию длины: два отрезка имеют одну и ту же длину, в случае, если при наложении они совпадают; в случае, если же один отрезок накладывается на часть другого не покрывая полностью, то протяженность первого меньше длины второго. Общеизвестны более сложные приемы, нужные для сравнения площадей плоских фигур, количеств пространственных тел.
Для сравнения двух предметов по массе их взвешивают. В случае, если чаши весов уравновешиваются, то предметы имеют однообразную массу, в случае, если же чаши не уравновешены, то предмет, пребывающий на той чаше, которая перетягивает, имеет громадную массу, второй предмет — меньшую.
Понятия длины, площади, количества, веса смогут быть обобщены на любой род размеров: в совокупности всех однородных размеров, т. е. всех длин, всех площадей, всех количеств, всех весов и т. д., устанавливается отношение порядка. Две величины а и Ь одного и того же рода либо совпадают (а=Ь), либо первая меньше второй (а
Однородные размеры возможно кроме этого складывать. К примеру, в случае, если точка В лежит между точками А и С, то протяженность отрезка АС равна сумме длин отрезков АВ и ВС (илл. 16, А).
В случае, если плоская фигура складывается из двух частей, не имеющих вторых неспециализированных точек, не считая граничных, то площадь S всей фигуры равна сумме площадей S1+S2 этих частей (илл. 16, Б).
| В случае, если предмет складывается из двух частей, то его масса т равна сумме m\+ni2 весов т\ыгп2 этих частей. |
В случае, если пространственная фигура складывается из двух частей, все неспециализированные точки которых образуют их неспециализированную границу, то количество всей пространственной фигуры равен сумме 1+2 количеств Щ и i этих частей (илл. 16, В).
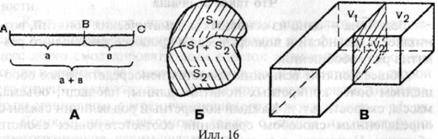
Так раскрывается суть операции сложения для каждого рода размеров (длин, площадей, количеств, весов и т.д.).
Исходя из смысла отношения меньше (
1) Отношение есть, как и между числами, антирефлексивным, т. е. -i(o
2) В случае, если а
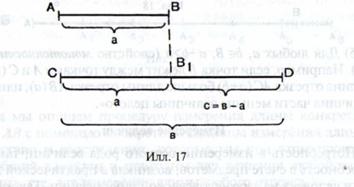
3) Сложение размеров, как и сложение чисел, владеет свойством переместительности (коммутативности): a+b=b+a для любых я, be В.
К примеру, безразлично — присоединить к отрезку АВ длины а отрезок ВС длины b либо напротив — мы все равно возьмём в следствии одинаковый отрезок.
4) Сложение размеров владеет свойством сочетательности (ассоциативности):
a+(b+c)=(a+b)+c для любых а, Ь, се В.
К примеру, в случае, если присоединить к отрезку АВ длины а отрезок BD длины Ь+с так, дабы точка В лежала между точками А и D (илл. 18), то возьмём отрезок AD длины а+ф+с); в случае, если к отрезку АС длины а+b присоединить отрезок CD длины с, то возьмём отрезок AD, протяженность которого выражается через (а+Ь)+с; но так как мы взяли одинаковый отрезок AD, то a+(b+c)=(a+b)+c. Исходя из этого возможно писать без скобок а+Ь+с.
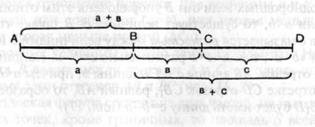
Илл. 18
5) Для любых a, be В, а+Ьа (свойство монотонности сложения). К примеру, в случае, если точка Я лежит между точками А и С (илл. 18), то протяженность отрезка АС (а+b) больше длины отрезка АВ (а), либо по большому счету «величина части меньше величины целого».
Измерение размеров
Потребность в измерении всякого рода размеров, так же как потребность в счете предметов, появилась в практической деятельности человека на заре людской цивилизации. Так же как для определения численности множеств, люди сравнивали разные множества, разные однородные размеры, определяя в первую очередь, какая из сравниваемых размеров больше, какая меньше. Эти сравнения еще не были измерениями. В будущем процедура сравнения размеров была усовершенствована. Одна какая-нибудь величина принималась за эталон, а другие величины того же рода
(длины, площади, количества, массы и т.п.) сравнивались с эталоном. В то время, когда же люди овладели знаниями о их свойствах и числах, величине-эталону приписывалось этот 1 эталон и число начал называться единицей измерения. Цель измерения стала более определенной — оценить, сколько единиц содержится в измеряемой величине. Итог измерения начал выражаться числом.
Задача измерения размеров, так же как и задача определения численности множеств предметов, есть источником, порождающим числа. Но в отличие от первой задачи, ответ которой абсолютно обеспечивается натуральными числами, для задачи измерения размеров этих чисел слишком мало. Это наглядно обнаруживается описанием процедуры измерения на несложном примере измерения длин.
Пускай нужно измерить длину отрезка АВ посредством единицы измерения CD длины е (илл. 19). 
Не смотря на то, что мы обрисуем процедуру измерения длины конкретного отрезка АВ посредством конкретной единицы измерения длины е, все рассуждения и действия, каковые мы наряду с этим совершим, общ и пригодны для ответа любой задачи этого типа, т. е. для измерения длины любого отрезка.
Откладываем отрезок CD от точки А последовательно на отрезке АВ, наряду с этим вероятны следующие случаи.
1. Быть может, что отрезок CD отложится на отрезке АВ целое число раз. На илл. 19, А, к примеру, 5 раз (а по большому счету п раз), т.е. второй финиш отрезка CD (точка D) при пятом (а в общем случае при п-м) отложении сходится с точкой В (финишем отрезка АВ).
Так как протяженность отрезка АВ равна 5е (пе), то, принимая длину е за 1, можно считать числовое значение длины отрезка АВ равным 5 (в общем случае — я).
В случае, если обозначить числовое значение длины отрезка АВ через \АВ\ (в будущем для краткости вместо «числовое значение длины» будем говорить легко «протяженность» в том месте, где это не ведет к недоразумению), то в отечественном примере |/4i?|=5, а в общем случае \АВ\=п. В этом случае натуральные числа снабжают ответ задачи измерения.
2. Быть может, что точка А$ (А„) не сходится с точкой В (илл. 19, Б), причем |Л5.В|
В этом случае мы можем только приближенно вычислять длину отрезка АВ равной одному из этих чисел, 5 либо 6 (я либо п+1). В следствии приобретаем приближенное значение измеряемой длины с точностью до 1. Это указывает, что, принимая одно из этих чисел за значение длины отрезка АВ, мы допускаем погрешность, меньшую 1, причем число 5 (я) — приближенное значение длины с недочётом, а число 6 (я+1) — с избытком. В случае, если точка В ближе к точке А^ (А„), то число 5 (я) ближе к подлинному (правильному) значению длины отрезка АВ, в случае, если же точка В ближе к точке А^ (А„+\), то число 6 (я+1) ближе к правильному значению данной длины. В зависимости от этого выбирают то приближенное значение, которое ближе к правильному, что дает меньшую погрешность.
В случае, если такая степень точности удовлетворяет нас, то можно считать процесс измерения законченным. Но практика довольно часто предъявляет требование взять результаты измерений с более высокой степенью точности, т. е. с меньшей погрешностью.
С целью этого появляется необходимость продолжить процесс измерения, т. е. измерить длину остатка, отрезка Аф, в общем случае АпВ. Конечно, это нельзя сделать посредством той же единицы измерения CD, которая не умещается на этом отрезке. Нужно выбрать более небольшую единицу измерения, какую-то часть отрезка CD, допустим десятую. Тогда протяженность е\ данной новой единицы измерения равна 0,1е, т.е. числу 0,1 (тут неявно используется свойство о возможности деления величины на какое угодно число частей).
Потом процедура измерения повторяется, но уже применительно к отрезку Аф (АпВ) и с единицей измерения длины 0,1. Значит, снова вероятны два случая:
1) Новая единица измерения уместится на отрезке Аф (А„В) целое число раз, к примеру 3 раза, а по большому счету п{ раз, где «i 10, так как прошлая единица измерения е не умещается на отрезке А„В. В этом случае И-#1=5,3 (\АВ\=п, п{), т.е. для выражения числового значения длины уже потребовалось дробное число (мы забрали десятую долю первой единицы в качестве второй единицы измерения, дабы возможно было воспользоваться десятичными дробями).
2) Новая единица измерения не належится целое число раз, т. е. точка В не сходится с финишем накладываемой единицы измерения. В этом случае приобретаем, к примеру, 5,3
В случае, если такая точность удовлетворительна, то процесс измерения можно считать законченным. В другом случае процесс длится, т. е. повторяется та же процедура, но уже применительно к новому остатку, отрезку А^^В, и с новой единицей намерения, протяженность которой, к примеру, десятая часть прошлой единицы, т.е. ^2=0,01. Увидим, что возможно было бы принимать 61=72 е, e2~xh еь и тогда были бы взяты приближенные значения длины в виде бинарных дробей.
В следствии приобретаем, к примеру, или \АВ\=5,36 (]АВ\=п, п\п2), или 5,36
В случае, если такая точность достаточна для решаемой задачи, то процесс измерения считается законченным, в другом случае он длится, т. е. процедура измерения повторяется применительно к новому остатку и с новой единицей измерения.
Конечно появляется вопрос: до каких пор может длиться процесс измерения?
Выясняется, по большому счету вероятны два случая: 1) на каком-то этапе процесса измерения единица измерения уложится целое число раз на измеряемом отрезке; 2) ни на каком этапе процесса измерения это не произойдёт и, следовательно, процесс измерения не будет прекращаться вечно.
Последнее событие свидетельствует, что существуют так именуемые несоизмеримые отрезки, к примеру его сторона и диагональ квадрата. В случае, если измерять диагональ квадрата стороной, т. е. принимая сторону квадрата за единицу измерения, то процесс измерения ни при каких обстоятельствах не закончится, поскольку ни сама сторона квадрата, им каждая ее часть, полученная от деления стороны на целое число равных частей, не укладывается целое число раз в диагонали этого квадрата. В этом случае и рациональных чисел, т. е. целых и дробных, слишком мало для ответа задачи измерения. В математике данный пробел устраняется предстоящим расширением совокупности чисел посредством введения иррациональных чисел. Как Как мы знаем из школьной математики, иррациональные числа представляются в виде нескончаемых десятичных непериодических дробей и образуют, так, вместе с рациональными числами множество вещественных (либо настоящих) чисел, т. е. объединение множеств рациональных и иррациональных чисел.
Но лишь теоретически процесс измерения может оказаться нескончаемым. Фактически же процесс измерения длин (и других размеров) складывается из конечного числа шагов, что дает в следствии приближенное значение измеряемой величины с любой требуемой степенью точности, зависящей от количества выполненных шагов в ходе измерения.
2.6. Методы
Что такое метод
Воспитание детей с самого рождения, в частности воспитание дошкольников, включает усвоение ими разнообразные правил и их строгое исполнение (правила утреннего туалета, раздевания и одевания, принятия пищи, перехода улицы и др.). Режим дня дошкольника является системой предписаний о исполнении воспитателем и детьми действий в определенной последовательности. Обучая детей счету, измерению длин, вычитанию и сложению чисел, уборке помещения, посадке растений и т. д., мы информируем им нужные правила о том, что и в какой последовательности следует сделать для исполнения задания. Организовывая разнообразные дидактические и подвижные игры, мы знакомим дошкольников с их правилами.
О всех видах деятельности, осуществляемых по определенным предписаниям, говорят, что они выполняются по определенным методам. С малых лет человек усваивает и выполняет в ежедневной судьбе много методов, довольно часто кроме того не зная, что это такое.
Что такое метод? Часто видятся виды однотипных задач, к примеру: сложение двух многозначных чисел; переход улицы, регулируемый либо нерегулируемый светофором; измерение длины отрезка и т. д. Конечно появляется вопрос: существует ли достаточно неспециализированный метод, что возможно было бы применять для ответа любой задачи данного вида однотипных задач?
В случае, если таковой неспециализированный метод существует, то его именуют алгоритмом^ данного вида задач. Для каждого из вышеприведенных видов задач имеется соответствующий метод.
1 Слово метод происходит от имени известного математика IX в. аль-Хорезми, что свидетельствует «из Хорезма», в первый раз сформулировавшего правила исполнения арифметических действий над многозначными числами. Через труды аль-Хорезми в Европу пробрались методы действий с числами в десятичной совокупности счисления, каковые нарекли методами в соответствии с латинской транскрипции имени ученого. В течение столетий значение слова «метод» понемногу обобщалось, и сейчас под методом знают некий неспециализированный способ либо метод, предписание, инструкцию, свод правил для ответа за конечное число шагов любой задачи из определенного вида однотипных задач, для которого рекомендован данный способ.
Для задачи сложения двух многозначных чисел известен метод сложения «в столбик», пригодный для сложения любых двух многозначных чисел, т. е. для ответа любой личной задачи из этого вида однотипных задач.
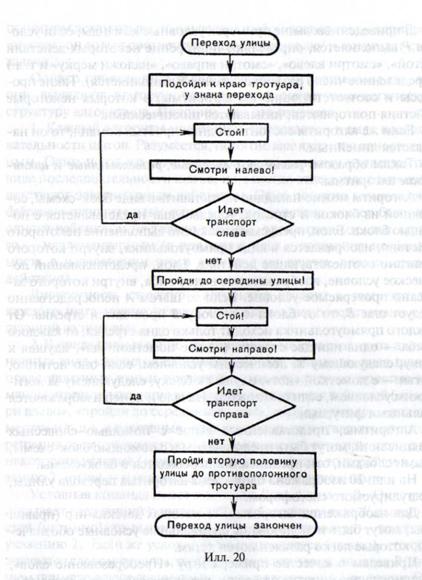
Для задачи перехода улицы, к примеру нерегулируемого светофором, возможно сформулировать неспециализированный метод в виде следующего предписания, складывающегося из 10 указаний, либо команд:
1. Подойди к краю тротуара у символа перехода.
2. Находись.
3. Наблюдай налево.
4. В случае, если идет транспорт слева, то перейди к указанию 2, в противном случае — к указанию 5.
5. Пройди до середины улицы.
6. Находись.
7. Наблюдай направо.
8. В случае, если идет транспорт справа, то перейди к указанию 6, в противном случае — к указанию 9.
9. Пройди вторую половину улицы до противоположного тротуара.
10. Переход улицы закончен.
Интуитивно под методом знают общепонятное и правильное предписание о том, какие конкретно действия и в каком порядке нужно выполнить для ответа любой задачи из данного вида однотипных задач.
Это определение, очевидно, не есть математическим определением в строгом смысле, поскольку в нем видится довольно много терминов, суть которых не смотря на то, что и интуитивно возможно ясен, но точно не выяснен («предписание», «общепонятное», «правильное», «воздействие»). Но оно является разъяснением того, что в большинстве случаев вкладывается в интуитивное понятие метода, а для отечественных целей этого достаточно.
Какие конкретно же особенности характеризуют каждый метод?
Анализ разных методов разрешает выделить следующие неспециализированные особенности, свойственные методам:
а) массовость, т. е. метод рекомендован для ответа не одной какой-нибудь задачи, а для ответа любой задачи из данного вида однотипных задач;
б) определенность (либо детерминированность), т. е. метод
представляет собой строго определенную последовательность
шагов, либо действий, он конкретно определяет первый ход и
любой следующий ход, не оставляя решающему задачу никакой
свободы выбора следующего шага по собственному усмотрению;
в) результативность: решая любую задачу из данного вида
задач по соответствующему методу, мы за конечное число
шагов приобретаем итог. Очевидно, для разных частных
задач одного вида число шагов может оказаться разным, но
оно в любой момент само собой разумеется.
Метод — одно из фундаментальных научных понятий, применяемое и математикой, и информатикой — наукой, изучающей методы представления, преобразования и хранения информации посредством разных автоматических устройств. Наличие метода для осуществления некоей деятельности есть нужным условием передачи этого вида деятельности разным автоматическим устройствам, роботам, компьютерам (от отпуска стакана газированной воды, продажи авиабилета с преобразованием и хранением информации о наличии свободных мест до управления сложными технологическими процессами, не говоря уже о исполнении огромных количеств вычислительной работы, которая связана с ответом непростых научно-технических задач).
Имеются разные формы записи либо представления методов, предназначенные для разных исполнителей: словесные предписания, а также включающие разные формулы; наглядные блок-схемы, ориентированные на исполнителя-человека; программы, воображающие собой запись метода на языке, понятном ЭВМ, т. е. языке программирования.
Тут уместно уточнить, что свидетельствует выдвинутое требование «общепонятности» предписания, которым задается метод. Это указывает, что предписание должно быть сформулировано так, дабы оно было одинаково ясно всем исполнителям той категории, на которую оно ориентировано. Это имеет очень серьёзное значение, например, при обучении мелких детей. К примеру, вышеприведенные предписания, задающие измерения перехода длины и алгоритмы улицы, не предназначены для обучения дошкольников. Для данной цели необходимо сформулировать их на понятном детям языке, что совершает любой воспитатель, в случае, если, очевидно, он имеет соответствующую подготовку и понимает свои задачи.
Но вышеприведенные предписания составлены так, что они выявляют шаговую (дискретную) оперативно-логическую структуру методов. Поясним, что это указывает.
1. Любой метод возможно представлен в виде последо-
вательности шагов. Очевидно, понятие ход есть относитель-
ным. Одинаковый метод возможно по-различному представить в
виде последовательности шагов, и не всегда отдельные шаги соот-
ветствуют элементарным действиям. Само понятие элементарное
воздействие довольно: одно да и то же воздействие возможно для
одного ребенка, и не только ребенка, элементарным, для друго-
го — неэлементарным (в следствии чего и появляется необходи-
мость в расчленении этого действия на другие, элементарные,
действия).
Дискретность структуры метода пребывает в том, что для каждого шага возможно указать конкретно конкретно следующий за ним ход.
2. В вышеприведенных предписаниях возможно различить два ос-
новных вида команд, а следовательно, два главных вида шагов,
представленных этими предписаниями методов: простые ко-
манды, предписывающие исполнение некоторых действий («смот-
ри влево», «пройди до середины улицы», «выбери мерку», «наложи
мерку» и т. д.), и составные, определяющие разветвление процесса
ответа задачи в зависимости от исполнения либо невыполнения
некоего условия («в случае, если идет транспорт слева, то перейди к ука-
занию 2, в противном случае — к указанию 5»), именуемые условными.
Условная команда имеет форму «в случае, если Р, то А, в противном случае В». Она предписывает следующий порядок действий: в случае, если условие Р выполняется (действительно), то выполняется А (в отечественном примере — возврат к указанию 2). В случае, если же условие Р не выполняется (ложно), что обозначается словом «в противном случае», то А пропускается и выполняется В (в отечественном примере осуществляется переход к следующему указанию 5).
Условные команды возможно записать сокращенно: «в случае, если Р, то А», наряду с этим подразумевается, что в случае, если условие Рне выполняется, то осуществляется переход к следующей по порядку команде В вышеприведенных примерах условные команды, в случае, если условие Р выполняется, определяют повторение некоторых действий («находись», «наблюдай влево», «наблюдай вправо», «наложи мерку» и т. д.) определенное число раз (до тех пор пока условие Р выполняется). Такие процессы и соответствующие им методы, в которых кое-какие действия повторяются, именуются циклическими.
В случае, если же метод складывается из одних несложных команд, то он именуется линейным.
Так, различают линейные, разветвленные и циклические методы.
Метод возможно наглядно представить в виде блок-схемы, складывающейся из блоков и стрелок. Любой ход представляется посредством блока. Блок, предусматривающий исполнение некоего действия, изображается в виде прямоугольника, в которого записано соответствующее воздействие. Блок, воображающий логическое условие, изображается в виде ромба, в которого записано контролируемое условие. В случае, если за шагом А следует ход В, то от блока А к блоку В проводится стрелка. От каждого прямоугольника исходит лишь одна стрелка, от каждого ромба — одна либо две стрелки (одна с пометкой «да», идущая к блоку, следующему за логическим условием, если оно действительно, вторая — с пометкой «нет», идущая к блоку, следующему за логическим условием, если оно ложно). конец и Начало изображаются круглыми фигурами.
Методы, представленные выше посредством словесных предписаний, смогут быть представлены и посредством блок-схемы, иными словами, эти предписания переводятся в блок-схемы.
На илл. 20 изображена блок-схема метода перехода улицы, нерегулируемого светофором.
Для изображения методов некоторых детских игр (правил игры) смогут быть использованы особые условные обозначения, каковые легко разъясняются детям.
Приведем как пример игру «Преобразование слов», моделирующую понятие метод преобразования слов в данном алфавите.
В данной игре, а по существу серии игр, слова и буквы необыкновенные. Употребляется двухбуквенный алфавит, складывающийся из двухразличных фигур , к примеру кружочка и квадратика, либо из цифр 0 и 1. Словами мы именуем конечные цепочки из кружочков и квадратиков (во втором варианте конечные
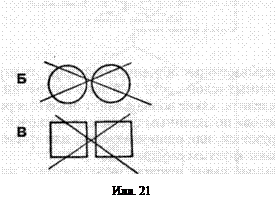последовательности из единиц и нулей). Любое сколь угодно долгое слово в отечественном алфавите преобразовывается по приведенным на илл. 21 правилам следующим образом: в случае, если в заданном слове имеется квадратик, расположенный левее кружочка, то, в соответствии с правилу 1, их необходимо поменять местами; в случае, если во снова взятом слове снова имеется квадратик, расположенный левее кружочка, необходимо снова их поменять местами и т.д.; правило 1 используется столько раз, сколько быть может, т. е. пока не окажется слово, в котором уже нет квадратика, расположенного левее кружочка, либо в котором все кружочки лежат левее всех квадратиков; после этого переходим к применению правила 2, то есть: в случае, если имеются два рядом стоящих кружочка, их удаляют, и правило 2 используется столько раз, сколько быть может, т. е. пока не окажется слово, в котором нет двух рядом стоящих кружочков; после этого переходим к применению правила 3, то есть: в случае, если имеются два рядом стоящих квадратика, их удаляют, и это правило используется столько раз, сколько быть может, т. е. пока не окажется слово, в котором нет двух рядом стоящих квадратиков. Полученное слово результат преобразования исходного слова по способу и заданным правилам их применения, определяющим совместно некий метод преобразования слов в данном алфавите.
| На илл. 22 продемонстрировано преобразование четырех слов по этому методу. |
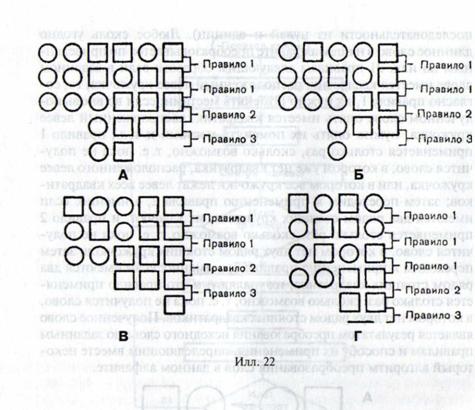
Как показывает опыт обучения, повторив эту игру пара раз для разных «слов», дети 5—6 лет в состоянии заблаговременно верно выяснить, какие конкретно по большому счету могут быть результаты сокращения «слов» по заданным правилам: квадратик и кружочек, либо один кружочек, либо один квадратик, либо «ничего» (это «ничего» именуют «безлюдным словом»).
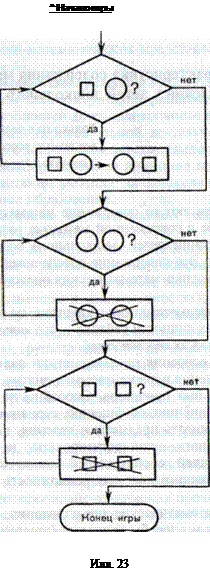
Вышеприведенные правила игры вместе с процедурой их применения смогут быть изображены блок-схемой (илл. 23).
Умение использовать разнообразные методы, тем более умение предвидеть и обосновывать вероятные результаты их применения — показатель формирования характерного для математика стиля мышления. Моделирование разных методов в виде
 |
детских игр открывает много возможностей для создания зачатков этого стиля мышления уже у дошкольников.
Глава 3. технологии и Содержание развития математических представлений у детей дошкольного возраста
3.1. Неспециализированная черта содержания математических представлений у детей дошкольного возраста
Лишь то в человеке прочно и надежно, что всосалось в природу его в первую пору судьбы.
Я. А. Коменский
Малыши постигают то содержание математической направленности, которое в современной методике развития математических представлений детей дошкольного возраста именуется предматематикой. Это содержание снабжает развитие мышления, освоение логико-способов познания и математических представлений.
Содержание предматематики направлено на развитие наиболее значимых составляющих личности ребенка — его интеллекта и интеллектуально-творческих свойств.
Результатами освоения предматематики являются не только знания, представления и элементарные понятия, но и неспециализированное развитие познавательных процессов. Способности к абстрагированию, анализу, сравнению, обобщению, сериации и классификации, умение сравнивать явления и предметы, выяснять закономерности, обобщать, конкретизировать и упорядочивать являются ответственной составляющей логико-математического опыта ребенка, что дает ему возможность самостоятельно познавать мир.
Освоенные математические представления, логико-способы познания и математические средства (эталоны, модели, обращение, сравнение и др.) составляют начальный логико-математический опыт ребенка. Данный опыт есть началом познания окружающей действительности, первым вхождением в мир математики.