3. область применения и Общая оценка способа средней неточности.
есть общепризнанным, что способ средней неточности дает самые низкие значения порога по сравнению с другими способами. Это разъясняется, по-видимому, активной сенсомоторной деятельностью субъекта, т.е. возможностью регулировки самим испытуемым стимуляции и связанным с этим привлечением вторых источников информации (кинестезии) для ответа стоящей перед ним задачи, и громадным, в большинстве случаев, временем действия стимула, а, следовательно, возможностью более полного извлечения информации из стимуляции.
Процедура подравнивания весьма естественна и легко принимается всеми испытуемыми — взрослыми и детьми. Это расширяет область ее применения по сравнению с другими способами. Способ подравнивания оказывается незаменим при оценке чувствительности в любых ситуациях, в то время, когда сенсорная чувствительность оператора есть средством (орудием), применяемым оператором при ответе опытных задач в ходе трудовой деятельности, как, к примеру, у фотометриста, определяющего плотность вещества методом подгонки к эталону, либо токаря, обтачивающего подробность с точностью до микрона.
Самый адекватно использование МСО в тех случаях, в то время, когда требуется оценка точки субъективного равенства. Конкретно этим разъясняется достаточно широкое использование способа в шкалирующих процедурах.
Значительно ограничивает область применения способа средней неточности необходимость обеспечения плавной регулировки стимуляции, что, со своей стороны, возможно достаточно непростой технической проблемой.
§ 3. Способ постоянных раздражителей
Другие заглавия этого способа — способ констант, частотный способ, способ подлинных и фальшивых случаев. Способ пребывает в предъявлении испытуемому последовательности стимулов, неизменных в течение всего опыта, и наименование из этого — способ постоянных раздражителей (МПР), способ констант. При измерения разностного порога предъявляется обычный стимул и сравниваемый с ним. Потому, что параметры стандартного и сравниваемого стимулов в течение всего опыта неизменны, любой из сравниваемых стимулов образует со стандартным постоянную отличие. Из этого еще одно наименование этого способа — способ постоянных отличий. Ярким результатом опыта являются частоты ответов, из которых значения порога находятся вычислительным методом. Эта особенность выяснила еще одно наименование этого способа — способ частот.
Способ констант пользуется славой самого правильного и надежного, потому, что сама процедура способа предусматривает такую организацию стимуляции, которая исключает ожидания и ошибки привыкания. Возможность накопления громадной статистики ответов, которая связана с ограничением числа постоянных раздражителей, используемых в измерении, повышает надежность измерения порога этим способом. Универсальность способа констант обусловлена, по-видимому, двумя событиями. Во-первых, он ставит менее твёрдые требования к выходным устройствам задающей аппаратуры, чем способ средней неточности, потому, что точную дискретную регулировку выходного сигнала взять технически значительно проще. Это существенно расширяет область применения МПР. Во-вторых, дискретность стимуляции разрешает применять, не считая суждений, и другие ответные реакции организма, к примеру, вегетативные, электроэнцефалографические, сосудистые и др. Эти реакции отличаются двумя серьёзными для измерения чувствительности особенностями: 1) не поддаются произвольному контролю (без особой тренировки), 2) их величина изменяется градуально. Применение этих реакций значительно расширяет область приложения МПР, потому, что снабжает его использование в тех случаях, в то время, когда исследователю нереально (либо некомфортно) применять речевой ответ для измерения порога (к примеру, в случаях симуляции, у детей, еще не овладевших речью, у животных). Помимо этого, использование непроизвольных реакций разрешает расширить количество информации, извлекаемой из опыта, потому, что информация об изучаемом ходе содержится не только в факте появления/не появления реакции, но и в ее величине, форме и скрытом периоде, исходя из этого возрастает количество сведений, которое возможно извлечено из каждой градуальной реакции.
Давая неспециализированную чёрта способа констант, нельзя не отметить еще одного момента. Способ констант занимает особенное место среди хороших способов измерения чувствительности в связи с тем, что практически все теоретические построения психофизики довольно пороговой неприятности для собственного экспериментального подтверждения обращались к этому способу. Он был самый гибким, приобретаемые этим способом результаты обнаружили объяснение в русле самых разных психофизических концепций.
1. Определение разностного порога способом констант.
Процедура. В предварительных опробованиях экспериментатор ориентировочно определяет пороговую территорию, т.е. тот диапазон различия стимулов, на границах которого испытуемый начинает фактически постоянно ощущать отличие эталонного стимула от сравниваемого. После этого экспериментатор выбирает в пределах данной территории ограниченный последовательность стимулов, каковые будут сравниваться с эталоном (значительно чаще 5—7). Выбор производится с таким расчетом, дабы самый не сильный среди них вызывал у испытуемого ответ “больше” в 5—10% случаев, а самый сильный — в 90—95%. Сравниваемые стимулы выбираются так, дабы расстояния между ними на стимульной оси были однообразными. Последнее требование снабжает некое упрощение статистической обработки данных и есть легко требованием удобства. При определении разностного порога стимулы предъявляются парами — эталон и сравниваемый — в один момент либо последовательно. Стимульная последовательность, составленная из пар стимулов, есть по своим особенностям случайной, но сбалансированной: любая пара предъявляется равное число раз, частота предъявления каждой пары распределена на последовательности равномерно. Конечно, что эта последовательность составляется до опыта и испытуемому малоизвестна. В большинстве случаев в опыте любая пара стимулов повторяется 20—200 раз.
В экспериментальной практике употребляются два различных метода объединения стимулов в пары: 1) место эталона в паре изменяется по случайному закону; 2) место эталона и сравниваемого стимула в паре фиксированы. Первый вариант ответа имеет то преимущество, что разрешает компенсировать постоянные неточности типа пространственной и временной на протяжении самого опыта. Сильным доводом в пользу второго метода есть уменьшение вариативности результатов опыта за счет уменьшения колебаний критерия при выборе испытуемым ответа в каждой отдельной пробе. По-видимому, направляться предпочитать второй метод, а пространственную неточность возможно учесть, в случае, если в одной стимульной последовательности эталон предъявляется слева, а в второй — справа. Подобным образом возможно распознать и временную неточность.
В каждой пробе, т.е. при предъявлении пары стимулов, испытуемый обязан вынести суждение, появилось ли чувство различия и каково оно. В способе констант употребляются две (“больше”, “меньше”) либо три категории ответов (“больше”, “меньше”, “равняется”). В любом случае порог вычисляется из пропорций суждений разнообразные на каждую несколько стимулов.
Психометрическая функция.
Разглядим случай, в то время, когда испытуемый дает две категории ответов — “больше” и “меньше”. Обозначим Sst— обычный стимул, а Svar— сравниваемый по исследуемому параметру (один из постоянных стимулов). В случае, если Svarсущественно меньше Sst, то испытуемый редко дает ответ “больше”, в случае, если же Svarзначительно больше Sst, то практически в любое время испытуемый дает ответ “больше”. В промежутке между этими двумя значениями при повышении изменяемого параметра стимула пропорция ответов “больше” медлено возрастает от 0 до 1. Исходя из этого пропорцию ответов “больше” комфортно применять при представлении результатов опыта в виде графика, именуемого психометрической функцией.
В случае, если в опыте предъявить большое число раз пара пар Svar, Sstи представить полученные эти на графике, где по абсциссе отложена физическая мера стимулов, а по ординате для каждого стимула указана пропорция ответов “больше”, то точки, обрисовывающие ответные эти, образуют кривую, имеющую, в большинстве случаев, S-образную форму. В случае, если выбрать некое новое значение сравниваемого стимула, которое лежит между уже опробованными, и повторить опыт, то соответствующая ему новая точка придется между двумя ветхими. Это дает основание заключить, что для любой пары стимулов S и Sstсуществует возможность P(Svar) ответа “Svarбольше Sst”. Психометрической функцией именуется такая функция P довода S, которая есть монотонной, дифференцируемой и ограничена единицей и нулём (Урбан, 1907). Оценкой ее значений помогают пропорции ответов “больше”. Из ограниченности и дифференцируемости единицей и нулём возможно сделать вывод о существовании соответствующей ей дифференциальной функции распределения. Принятые в психофизике изображения психометрической и дифференциальной кривой распределения, взятых в опыте, совершённом способом констант с двумя категориями ответов, представлены на рис. 5.
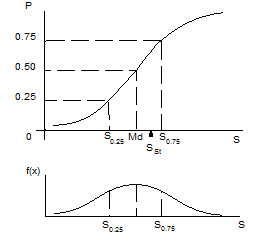 |
Рис. 5. Психометрическая функция и соответствующая ей дифференциальная кривая: оси абсцисс на обоих графиках — интенсивность сравниваемого стимула; ось ординат на верхнем графике — возможность ответов “больше”, ось ординат на нижнем графике — плотность возможности ответов “больше”
Форма психометрической кривой. S-образная форма психометрической кривой допускается как пороговыми теориями Фехнера и Блеквелла, так и теориями непрерывности, не смотря на то, что интерпретация ее в том и в другом случае разна. Главная сущность любой пороговой теории сводится к утверждению о существовании порога как настоящего принципа работы сенсорной совокупности. Порог понимается практически как барьер, критическое значение в континууме раздражений. Если бы значение порога было стабильно во времени, то психометрическая кривая имела бы вид линейной ступенчатообразной функции. Этого ни при каких обстоятельствах не бывает. Ее S-образная форма разъясняется тем, что порог флуктуирует во времени случайным образом. Разные варианты других теорий (Дельбеф, 1883; Мюллер, 1896; Ястров, 1888), отвергающие существование порога, исходили из предположения, что чувство есть постоянной функцией, зависящей от двух степени — предрасположенности и переменных интенсивности раздражителя человека к его восприятию. Потому, что последняя зависит от случайного сочетания множества тяжело учитываемых факторов, то их баланс есть случайной величиной и имеет обычное распределение. Конкретно исходя из этого и психометрическая кривая имеет S-образный вид интегральной функции обычного распределения. Фехнер (1860) кроме этого думал, что психометрическая функция есть интегральной функцией обычного распределения; эта точка зрения стала называться фи-гамма догадки. В ветхих работах хорошей психофизики j (фи) употреблялась для обозначения стимулов, а g (гамма) — для обозначения ответов. Терстон (1928) полагал, что потому, что в соответствии с закону Вебера различительная ступень растет с повышением стимула, психометрическая кривая получает хорошую асимметрию, пропорциональную дроби Вебера. Психометрическая кривая нормализуется, в случае, если забрать логарифмический масштаб по стимульной оси (jlogg-догадка). Различие психометрических кривых, взятых в пороговых опытах, столь незначительно, что тяжело дать предпочтение одной из этих догадок.
Нейроквантовая теория Стивенса, являющаяся по существу пороговой, предвещает прямолинейную психометрическую кривую, представленную на рис.6.
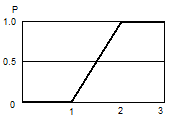 |
Рис. 6. Психометрическая функция, предсказанная нейроквантовой теорией Стивенса
В соответствии с данной теории, изменение в ощущении замечается в любой момент, в то время, когда дополнительное возбуждение, вызванное приращением стимула, возрастает на величину, равную одному нервному кванту. Порог различения отстоит от стандартного стимула в соответствии с данной теории на 1,5 стимульных промежутка, соответствующие нервному кванту. Фактор случайности в данной теории воплощается не в колебаниях порога, а в случайной величине остаточного возбуждения, суммируясь с которой добавочное возбуждение, вызванное приращением стимула, ведет к генерации нервного кванта. Предполагается, что условная единица стимульной оси является физическим аналогом величины кванта. Прямолинейность психометрической кривой обусловлена равномерным распределением величины остаточного возбуждения.
Параметры психометрической кривой. Как и в других пороговых способах для чёрта распределения результатов измерения в МПР употребляются меры центральной тенденции (медиана — Md и среднее арифметическое — M) и меры изменчивости (полумежквартильный размах — Q и стандартное отклонение — s ). Перпендикуляр из медианы дифференциальной кривой распределения дробит площадь под кривой пополам. Потому, что площадь под кривой равна единице, медиане соответствует стимул, для которого возможность ответа “больше” равна 0,5:
(15)
Полумежквартильный размах определяется как полуразность Q3и Q1:
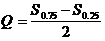 (16)
(16)
Сейчас в практике психофизических изучений стали довольно часто употребляться среднее арифметическое распределения — M и стандартное отклонение — ss. Как мы знаем, в симметричных распределениях Md и M совпадают, а меры изменчивости строго соотнесены:
ss= 1.483Q (17)
Психофизический суть параметров психометрической кривой.
Промежуток неопределенности оценивается через межквартильный размах (Q3- Q1):
IU = S0.75 — S0.2525 (18)
Точка субъективного равенства определяется как медиана: PSE=Md. Константная неточность имеет место при несовпадения медианы со стандартом и равна:
(19)
Разностный порог определяется в опыте с двумя категориями ответов как добрая половина промежутка неопределенности и соответствует полумежквартильному размаху психометрической кривой, выстроенной по ответам больше либо меньше. Обозначим его Q(2), где цифра в скобках говорит о количестве категорий ответа, а индекс Q выделяет, что порог характеризуется мерой разброса:
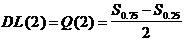 |
(20)
Психофизические показатели в опыте с тремя категориями ответов.
При применении трех категорий ответов испытуемого в способе констант — “больше”, “меньше” и “равняется” — психометрические кривые ответов “больше” и “меньше” не являются зеркальными и потому должны рассматриваться обе. Результаты 3-категориального опыта представлены на рис.7 и 8.
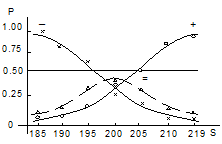 |
Рис.7. Психометрические кривые, полученные в опыте с тремя категориями ответов: — ответы “больше”, — “меньше”, — “равняется”

Рис. 8. Те же психометрические кривые, что и на рис. 7: кривая ответов “меньше” взята методом дополнения возможностей ответов “меньше” до 1, т.е. совершена через точки, полученные как (1-Р(-)); PSE — точка субъективного равенства; IU — промежуток неопределенности; Ll и Lh — нижний и верхний пороги различения, соответственно
В соответствии с принятым операциональным определением порога как 50% точки (см. пункт 2 в этом параграфе), которое возможно абсолютно применить к трехкатегориальному опыту, медиана психометрической кривой ответов “меньше” есть оценкой нижнего разностного порога, а медиана ответов “больше” — верхнего разностного порога; расстояние между ними характеризует промежуток неопределенности (IU), центр которого есть точкой субъективного равенства (PSE). За величину разностного порога одни исследователи (Урбан, 1907; Бардин, 1976) предлагают вычислять в соответствии с принятому в способе границ определению половину промежутка неопределенности, т.е.
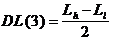 (21)
(21)
где DL(3) — обозначение указанной оценки разностного порога; Lh и Ll — величины верхнего и нижнего разностного порога, соответственно.
Другие исследователи предлагают применять в качестве пороговой меры различения полумежквартильный размах психометрической кривой ответов “больше” либо “меньше”. Обозначим эту оценку порога Q(3):
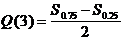
(22)
Эта оценка разностного порога, согласно точки зрения Каллера (1928), не зависит от частоты появлений ответов “равняется” и показалась как следствие неудовлетворенности психофизиков первой мерой DL(3), потому, что величина промежутка неопределенности во многом зависит от рвения испытуемого использовать нейтральные ответы. В действительности, при повышении частоты ответов “равняется” возрастает величина промежутка неопределенности (см. рис. 9), а следовательно, и разностного порога, в случае, если его оценивать как DL(3). Фернбергер (1931) продемонстрировал, что величина IU во многом зависит от инструкции, благодаря которой возможно руководить частотой ответа “равняется”. Он заключил, что испытуемые различаются по частоте потребления ответов “равняется” частично в силу различия темперамента, частично — в следствии различия в руководствах. Следовательно, величина IU характеризует вклад скорее процесса ответа, чем фактически сенсорной чувствительности.
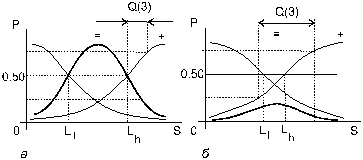 |
Рис. 9. Психометрические функции, полученные в МПР с тремя категориями ответов: а — много ответов “равняется”, б — незначительное количество ответов “равняется”
Но и вторая оценка порога различения Q(3) столь же подвержена критике. Гилфорд (1954), сравнивая оценки порогов по DL(3) и Q(3) продемонстрировал, что они измеряют различные размеры. В случае, если испытуемый сокращает число ответов “равняется”, крутизна психометрических кривых ответов “больше” и “меньше” значительно уменьшается, т.е. в один момент с уменьшением IU и DL(3) возрастает Q(3) (см. рис.9б). В случае, если же испытуемый по каким-либо обстоятельствам увеличивает число нейтральных ответов, соотношение размеров DL(3) и Q(3) изменяется в противоположном направлении (см. рис.9а). Из этого Гилфорд делает обоснованный вывод, что две оценки, каковые изменяются в противоположных направлениях, не могут служить мерой одного и того же.
Результатом обрисованной дискуссии явился отказ психофизиков от применения трех категорий ответов при измерении порогов способом констант: испытуемому или по большому счету не разрешается применять нейтральные ответы на протяжении опыта, или при разрешения нейтральные ответы делятся между ответами “больше” и “меньше”. Вопрос о том, как дробить ответы — поровну либо пропорционально количеству ответов двух вторых категорий — довольно много обсуждался, но исследователи так и не пришли к согласованному точке зрения.
При применении двухкатегориальной совокупности ответов единственной применяемой оценкой порога реакции есть величина Q(2), исходя из этого везде, где это только возможно, при работе МПР используются лишь две категории ответов.
Совет отказаться от трехкатегориальной совокупности ответов при измерении чувствительности способом констант не всегда приемлема. В тех случаях, в то время, когда требуется оценка различия сложных многомерных стимулов, испытуемый затрудняется классифицировать собственные ощущения в терминах “больше” — “меньше”, потому, что при трансформации одного параметра стимула может изменяться сходу пара сенсорных показателей действия, и испытуемый, “соскальзывая” с одного показателя на другой, может сломать опыт. По-видимому, самоё подходящим для оценки восприятия сложных стимулов, чаще всего видящихся в прикладных изучениях, есть способ, разрешающий испытуемому выносить суждение о различии стимулов, не “привязываясь” к какому-либо одному показателю, и снабжающий такую организацию опыта, которая разрешила бы уменьшить загрубляющее оценку фактически чувствительности влияние несенсорных факторов. Модификация способа АБХ, предложенная Индлиным (1978), по-видимому, удовлетворяет этим требованиям (см. пункт 3).
2. Определение безотносительного порога способом констант.
Процедура измерения полного порога от измерения разностного порога способом констант отличается лишь тем, что в каждой пробе испытуемому предъявляется один из нескольких (в большинстве случаев 5—9) постоянных стимулов, на что испытуемый дает один из двух вероятных ответов. Определение стимульного диапазона, количества предъявляемых стимулов, величины межстимульного промежутка осуществляется исходя из тех же мыслей, каковые учитывались при организации измерения дифференциального порога. Порядок предъявления стимулов кроме этого строится как сбалансированно случайный.
По взятым в опыте частотам ответов на любой из постоянных стимулов строится психометрическая кривая. За безотносительный порог принимается так называемая 50-процентная точка кривой, т.е. мера центральной тенденции (среднее M либо медиана Md, чаще медиана). По какой причине 50-процентная точка берется в качестве пороговой меры? С позиций пороговой концепции эта точка имеется медиана распределения моментальных значений порога, т.е. значений безотносительного порога в те моменты времени, в то время, когда происходит измерение. С позиций хорошей теории непрерывности ответ испытуемого имеется функции двух переменных — размеры стимула (чем больше, к примеру, интенсивность стимула, тем чаще ответ “Да”) и баланса благоприятных и негативных факторов различной природы. 50-процентной точке соответствует минимальное значение стимула, вызывающего чувство лишь при балансе благоприятных и негативных факторов.
Меры изменчивости, обрисовывающие полученное распределение, полумежквартильный размах — Q и стандартное отклонение — s, характеризуют надежность оценки порога.
Конечно, измеряя полный порог, мы должны отдавать себе отчет в том, что это не столько порог “чистого” ощущения, сколько порог реакции, т.е. величина, на которую воздействуют и несенсорные факторы. В частности, подлинное значение порога ощущения может искажаться за счет влияния случайного угадывания. Для корректировки таких ответов в рамках пороговой концепции Блэквеллом (1953) была предложена так называемая “поправка на случайный успех”. В соответствии с Блэквеллу, возможность верного ответа “Да” складывается из возможности подлинного восприятия предъявляемого стимула (Pc) и возможности случайного угадывания неощущаемого действия. Последняя величина равна возможности ответа “Да” (P”yes”) при отсутствии стимула (в противном случае именуемая фальшивой тревогой — Pfa), умноженной на возможность отсутствия ощущения при действии стимула, т.е.
(23)
откуда подлинная возможность верных ответов определяется из результатов опыта следующим образом:
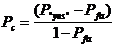 (24)
(24)
направляться не забывать, что исходной посылкой Блэквелла было отрицание какой-либо сенсорной базы ответов угадывания, с чем тяжело дать согласие, потому, что как мы знаем, что не весь опыт рефлексируется человеком.
Чтобы воспользоваться “поправкой на случайный успех”, нужно ввести в опыт так именуемые безлюдные пробы (пробы-ловушки), в то время, когда по окончании сигнала “Внимание” экспериментатор не предъявляет стимула. Появляющиеся в этих пробах ответы “Да” разрешат оценить возможность фальшивых тревог.
Разглядим пример определения безотносительного порога способом констант. Измеряется пространственный порог тактильного восприятия — то минимальное расстояние между двумя злимыми точками кожи, при котором испытуемый в 50% случаев дает ответ “два” и в 50% — ответ “один”. Выбрав участок кожи, на котором будет определяться порог, экспериментатор делает пара предварительных замеров эстезиометром, применяя, к примеру, процедуру способа границ, чтобы грубо выяснить пороговую территорию, в которой кое-какие предъявления стимула приводят к ответу “Два”, а кое-какие другие предъявления стимула — ответ “Один”. Экспериментатор выбирает 5 стимулов так, что мельчайший стимул приводит к ответу “Два” примерно в 5% случаев, а громаднейший — в 95%. Промежутки между стимулами равны. Предъявляются стимулы в сбалансированно-случайном порядке. Любой стимул предъявляется 100 раз. Экспериментальные эти приведены в таблице 1. Согласно этой информации строится психометрическая кривая. Для этого на графике по абсциссе откладывается физический параметр стимула — расстояние между злимыми точками в мм, а по ординате — пропорции ответов. Психометрическая кривая отечественного примера приведена на рис.10.
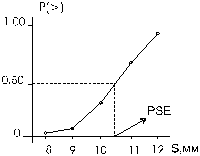 |
Рис. 10. Психометрическая кривая, выстроенная по итогам опыта по определению пространственного порога тактильного восприятия: точками продемонстрированы результаты экспериментов. Полученная кривая есть хорошим приближением к интегральной кривой обычного распределения (по Гилфорду, 1954)
Таблица 1
Результаты опыта по определению пространственного порога тактильного восприятия
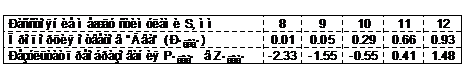 |
Очень редко случается так, что одному из стимулов соответствует пороговая пропорция ответов: P”два” = 0,5. Значительно чаще соответствующую порогу точку приходится определять по взятой психометрической кривой. Графическим либо вычислительным методом возможно определить значения медианы (и среднего), характеризующие величину безотносительного порога (в отечественном примере RL=10,57 мм) и меры вариативности — квартили Q3, Q1и стандартного отклонения — s.
Разумеется, что точность оценки порога обусловлена в первую очередь “хорошестью” аппроксимации экспериментально взятых точек ровной кривой. К сожалению, математически корректное ответ задачи подгонки точки непросто. Исходя из этого на практике употребляются два варианта построения психометрической функции: 1) посредством линейной интерполяции отдельных участков психометрической функции в линейных координатах; или 2) вся психометрическая функция аппроксимируется функцией обычного распределения, которое в обычных координатах есть прямой линией. Разглядим оба эти случая обработки экспериментальных данных.
Обработка экспериментальных данных в способе констант
Метод линейной интерполяции. Данный метод не снабжает высокую точность, но очень несложен. Линейная интерполяция основывается на представлении психометрической функции в виде отрезков прямой, каковые проводятся между взятыми точками. Данный случай представлен на рис. 11.
Несложным и чаще всего применяемым есть графический метод квартилей значений и нахождения медианы. В случае, если на графике совершить горизонтальные линии на уровне пропорций ответов, равных 0.5, 0.25, 0.75, то их пересечения с выстроенной психометрической кривой дадут, сответственно, значения Md, Q1и Q3, каковые считываются с оси абсцисс в физических размерах стимула. Конечно, при применении графического метода обработки результатов направляться выстроить психометрическую функцию на координатной бумаге, выбрав достаточно большой масштаб.
Те же значения смогут быть взяты и расчетным методом по следующим формулам (практически эти формулы вытекают из ответа прямоугольных треугольников):
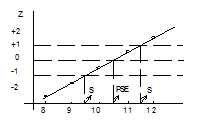 |
Рис. 11. Психометрическая функция, выстроенная по экспериментальным точкам с применением способа линейной интерполяции
Медиана психометрической кривой определяется как
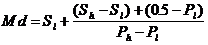 |