Уравнение вида именуется линейным дифференциальным уравнением порядка n.
В случае, если то оно именуется неоднородным, а вдруг , то однородным: .
Линейное однородное уравнение с постоянными коэффициентами:
.
В случае, если составить многочлен с теми же коэффициентами, и степенными функциями той же степени, что был на этом же месте порядок производной, то таковой многочлен именуется характеристическим, а уравнение — характеристическим уравнением.
Теорема 1. Функция есть ответом линейного однородного дифференциального уравнения имеется характеристический корень.
Подтверждение. Ищем ответ в виде .
В случае, если , то , , … .
Подставим в уравнение .
Возьмём .
Во всех слагаемых однообразная экспонента, вынесем её за скобку:
.
Но потому, что , то .
Что и требовалось доказать.
Итак, ответами смогут быть не все экспоненты, а только кое-какие избранные, не более n штук, в силу того, что многочлен степени n имеет не больше n разных корней.
Теорема 2. Линейная комбинация ответов линейного однородного дифференциального уравнения также есть его ответом.
Подтверждение.
Пускай и — два разных ответы уравнения
.
Другими словами, они оба обращают его в тождество:
и
.
Нужно доказать, что линейная комбинация также подходит в качестве ответа. Как мы знаем, что для производной, и и последующих выполняется свойство линейности: , исходя из этого , , и т.д.
Тогда, подставляя линейную комбинацию в дифференциальное уравнение, возьмём:
=
Но так как в каждой скобке 0, так как любая из этих функция была ответом уравнения. Получается .
Так, линейная комбинация ответов также есть ответом линейного уравнения.
Случай 1. Все характеристические корни настоящи и разны.
, . Тогда вероятные ответы это n разных экспонент: . Эта совокупность функций именуется «фундаментальная совокупность ответов» (ФСР). Но так как по теореме 2, каждая линейная комбинация также есть ответом, то все функции вида также решения.
именуется «неспециализированным ответом» дифференциального уравнения.
Пример.Решить уравнение .
Ответ. Характеристическое уравнение: , оно сводится к виду , корни , . Тогда ответами смогут быть лишь и . Сделаем диагностику для каждой из экспонент. Подставим каждую из них в уравнение.
1) = .
2) = .
Проверка выполнена. Обе экспоненты являются ответами.
Наряду с этим никакая третья экспонента не может служить решением этого же уравнения, в силу того, что характеристический многочлен 2-й степени, и он имеет максимум 2 корня.
ФСР складывается из и . Неспециализированное ответ: .
Случай 2.Все характеристические корни настоящие, но среди них имеется кратные.
В случае, если имеется корень кратности , то в совокупности ответов будут находиться , другими словами одну и ту же экспоненту раз включать в фундаменатльную совокупность ответов запрещено, в противном случае фактическое количество функций в ФСР окажется меньше, чем n.
Не считая самой экспоненты, необходимо забрать ещё и с домножением на степенные, по нарастанию степеней до .
Пример. Решить уравнение .
Ответ. Характеристическое уравнение: , другими словами , характеристическое корни . Тогда ФСР: , а неспециализированное ответ: .
Сделаем диагностику. Для разумеется. Удостоверимся в надежности .
, тогда , .
= = = = 0.
Случай 3. Не все корни настоящи (имеется комплексные характеристические корни).
В случае, если корень (и наряду с этим и ), то в ФСР, в числе всех других, входят две такие функции: и .
Пример. , таковой пример мы выше решали и вторым методом, а сейчас разглядим это уравнение как линейное. Характеристическое уравнение , корни , другими словами . Решения .
Теорема 3.(Теорема о наложении ответов). В случае, если — ответ линейного неоднородного дифф.уравнения с правой частью , а — ответ для того чтобы же дифф.уравнения, но с правой частью , то сумма есть ответом уравнения с правой частью .
Подтверждение. Доказывается подобно теореме 2.
Пускай правильно и
.
Тогда подставим сумму в левую часть: =
+ 
= .
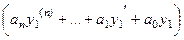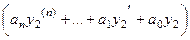Так, в случае, если в неоднородном уравнении правая часть имеет несколько слагаемых, то возможно решить более простые уравнения (для каждого из них раздельно) и сложить решения.
Замечание. Такое же утверждение правильно не только для суммы, но и для линейной комбинации. Тут коэффициенты равны 1 лишь для наглядности и простоты доказательства.
Следствие 1. Сумма ответов линейного неоднородного и соответствующего однородного дифференциального уравнения есть ответом неоднородного уравнения.
Подтверждение. В условиях прошедшей теоремы, забрать одну правую часть , а вторую . тогда сумма ответов есть ответом уравнения с правой частью .
Следствие 2. Разность двух разных ответов линейного неоднородного дифференциального уравнения есть ответом соответствующего однородного.
(Слово «соответствующего» тут свидетельствует, что с той же левой частью, что и было неоднородное).
Понятие линейной комбинации, которое разглядели выше, тут обобщено из векторной алгебры (отыскать в памяти совокупности векторов). Разглядим другие обобщения, к примеру, независимости системы и линейной зависимости.
Определение. Совокупность функций именуется линейно-свободной, в случае, если из равенства направляться, что все коэффициенты . В случае, если же это равенство допустимо при каком-то комплекте коэффициентов (т.е. не все они равны 0), то совокупность именуется линейно-зависимой.
Примеры. ЛЗС. Заберём коэффициенты 2 и .
. В случае, если в совокупности имеется хотя бы две пропорциональные функции, то совокупности ЛЗС.
ЛНС. Какими бы ни были коэффициенты, получается многочлен 2 степени , и тут 0 может оказаться, лишь только в том случае, если обнулить все коэффициенты.
ЛНС. Ни одна экспонента одной степени не представляется в виде второй экспоненты, умноженной на коэффициент.
Дабы узнать, ЛЗС либо ЛНС совокупность векторов, в линейной алгебре использовали определители. Тут же практически нет матрицы, поскольку легко n скалярных функций. Однако, оказывается, что тут также возможно достроить до квадратной матрицы, то есть посредством их производных. В случае, если во 2-й строке записать все их первые производные, в 3-й строке — вторые производные, и без того потом, до порядка, с той целью, дабы оказалась конкретно квадратная матрица, таковой определитель именуется определителем Вронского.
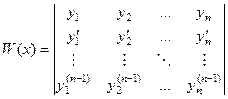
Разглядим определители Вронского в тех примерах, каковые были выше.
Совокупность функций .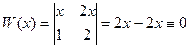 
Совокупность функций .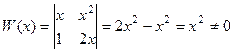 
.
Совокупность функций .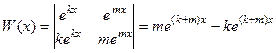 
=
, так как числа различные (разность в скобке точно не 0) а экспонента не равна 0.
Как видим на примерах, определитель Вронского для линейно зависимой совокупности оказался тождественно равен 0, а для свободных — нет. На следующей лекции докажем данный факт в общем виде:
Теорема 4. совокупность функций линейно-зависима.
Приложение 1. Вопросы на доказательства (для билетов).
Лекция № 1
1. Докажите формулу интегрирования по частям.
Лекция № 2
1. Доказать, что замена , где r = НОК (r1,…,rk) сводит интеграл к интегралу от рациональной дроби.
2. Доказать, что замена замена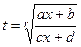 
сводит интеграл вида 
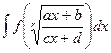к интегралу от рациональной дроби.
3. Вывести косинуса преобразования и формулы синуса
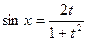
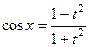для универсальной тригонометрической замены 
.
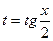4. Доказать, что при, в то время, когда функция нечётна относительно косинуса, замена сводит интеграл к рациональной дроби.
5. Доказать, что при, в то время, когда
замена: сводит интеграл к рациональной дроби.
6. Доказать, что для интеграла вида замена своит интеграл к рациональной дроби.
7. Доказать формулу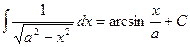 
8. Доказать, что для интеграла вида замена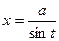 
своит интеграл к рациональной дроби.
9. Доказать, что для интеграла вида замена сводит интеграл к рациональной дроби.
Лекция № 3
1. Доказать, что функция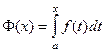 
есть первообразной от функции .
2. Доказать формулу Ньютона- Лейбница: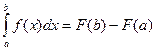 
.
3. Доказать формулу длины очевидно заданной кривой:
.
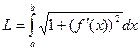4. Доказать формулу длины кривой, заданной в полярных координатах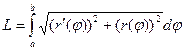 
Лекция № 4
Докажите теорему: сходится , сходится .
Лекция № 5
1. Вывести (доказать) формулу площади очевидно заданной поверхности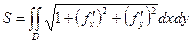 
.
2. Вывод формул перехода к полярным координатам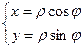 
.
3. Вывод определителя Якоби полярных координат .
4. Вывод формул перехода к цилиндрическим координатам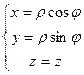 
.
5. Вывод определителя Якоби цилиндрических координат .
6. Вывод формул перехода к сферическим координатам:
.
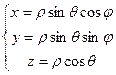Лекция № 6
1. Доказать, что замена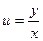 
сводит однородное уравнение к уравнению с разделяющимися переменными.
2. Вывести неспециализированный вид ответа линейного однородного уравнения.
3. Вывести неспециализированный вид ответа линейного неоднородного уравнения способом Лагранжа.
4. Доказать, что замена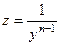 
сводит уравнение Бернулли к линейному уравнению.
Лекция № 7.
1. Доказать, что замена понижает на k порядок уравнения .
2. Доказать, что замена понижает на единицу порядок уравнения .
3. Доказать теорему: Функция есть ответом линейного однородного дифференциального уравнения имеется характеристический корень.
4. Доказать теорему о том, что линейная комбинация ответов линейного однородного дифф. уравнения также имеется его ответ.
5. Доказать теорему о наложении ответов: В случае, если — ответ линейного неоднородного дифф.уравнения с правой частью , а — ответ для того чтобы же дифф.уравнения, но с правой частью , то сумма есть ответом уравнения с правой частью .
Приложение 2.
Небольшие и устные вопросы на знание теории (для коллоквиумов).
Лекция № 1
1. Что такое первообразная и неизвестный интеграл, чем они отличаются?
2. Растолковать, по какой причине также есть первообразной.
3. Напишите формулу интегрирования по частям.
4. Какая замена требуется в интеграле вида и как именно она ликвидирует корни?
5. Запишите вид разложения подынтегральной рациональной дроби на несложные при, в то время, когда все корни разны и настоящи.
6. Запишите вид разложения подынтегральной рациональной дроби на несложные при, в то время, когда все корни настоящи, и имеется один кратный корень кратности k.
Лекция № 2.
1. Напишите, какое разложение рациональной дроби на несложные при, в то время, когда в знаменателе имеется множитель 2 степени с отрицательным дискриминантом.
2. Какая замена сводит интеграл к рациональной дроби?
3. Что такие универсальная тригонометрическая подстановка?
4. Какие конкретно замены производятся в случаях, в то время, когда функция под знаком интеграла нечётна относительно синуса (косинуса) ?
5. Какие конкретно замены производятся при наличия в подынтегральной функции выражений , , либо .
Лекция № 3.
1. Определение определённого интеграла.
2. Перечислите кое-какие из фундаментальных особенностей определённого интеграла.
3. Напишите формулу Ньютона-Лейбница.
4. Напишите формулу количества тела вращения.
5. Напишите формулу длины очевидно заданной кривой.
6. Напишите формулу длины параметрически заданной кривой.
Лекция № 4.
1. Определение несобственного интеграла (посредством предела).
2. Чем отличаются рода и 1 несобственные 2 интегралы.
3. Приведите простые примеры сходящихся рода 1 и 2 интегралов.
4. При каких сходятся интегралы (Т1).
5. Как сходимость связана с конечным пределом первообразной (Т2)
6. Что такое нужный показатель сходимости, его формулировка.
7. Показатель сравнения в конечной форме
8. Показатель сравнения в предельной форме.
9. Определение кратного интеграла.
Лекция № 5.
1. Смена порядка интегрирования, продемонстрировать на несложном примере.
2. Напишите формулу площади поверхности.
3. Что такое полярные координаты, напишите формулы перехода.
4. Чему равен якобиан полярной совокупности координат?
5. Что такое цилиндрические и сферические координаты, в чём их отличие.
6. Чему равен якобиан цилиндрических (сферических) координат.
Лекция № 6.
1. Что такое дифференциальное уравнение 1 порядка (неспециализированный вид).
2. Что такое дифференциальное уравнение 1 порядка, разрешённое относительно производной. Приведите какой-нибудь пример.
3. Что такое уравнение с разделяющимися переменными.
4. Что такое общее, частное ответ, условия Коши.
5. Что такое однородное уравнение, каков неспециализированный способ его решения.
6. Что такое линейное уравнение, в чём состоит метод его решения, что такое способ Лагранжа.
7. Что такое уравнение Бернулли, метод его решения.
Лекция № 7.
1. Какая замена нужна для уравнения вида .
2. Какая замена нужна для уравнения вида .
3. Продемонстрируйте на примерах, как возможно выразить в виде .
4. Что такое линейное дифференциальное уравнение порядка n.
5. Что такое характеристический многочлен, характеристическое уравнение.
6. Сформулировать теорему о том, при каком r функция есть ответом линейного однородного дифференциального уравнения.
7. Сформулировать теорему о том, что линейная комбинация ответов линейного однородного уравнения также имеется его ответ.
8. Сформулировать теорему о наложении следствия и решений из неё.
9. Что такое линейно-зависимая и линейно-свободная совокупности функций, привести какие-нибудь примеры.
10. Что такое определитель Вронского совокупности из n функций, приведите пример определителя Вронского для ЛЗС и ЛНС совокупностей.
Приложение 3. Задачи из лекций.
Лекция № 1
Пример. . Пример.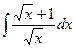 
.
Пример. . Пример. .
Пример. Пример. .
Пример.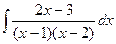 
. Пример. 
.
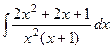Лекция № 2
Пример.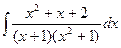 
. Пример. 
.
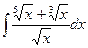Пример.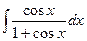 
. Пример. .
Пример.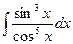 
. Пример. 
.
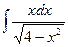Лекция № 3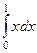 
, 
, 
, 
, 
.
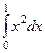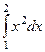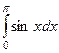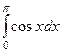Пример. Вычислить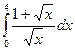 
.
Пример. Отыскать площадь фигуры, ограниченной линиями .
Пример. Вывести формулу количества шара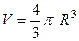 
.
Лекция № 4
Вычислить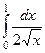 
, , 
, 
.
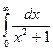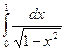Узнать сходимость: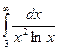 
, 
.
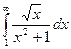Вычислить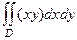 
, где имеется квадрат: , .
Вычислить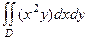 
, D треугольник с вершинами (0,0), (1,0), (1,1).
Лекция № 5.
Пример. Поменять порядок интегрирования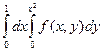 
.
Пример. Вычислить интеграл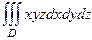 
где D куб .
Пример. Вычислить интеграл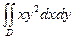 
где D — четверть круга единичного радиуса в первой четверти плоскости.
Пример. Доказать формулу площади круга посредством полярных координат.
Пример. Посредством сферических координат вывести формулу количества шара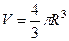 
.
Лекция № 6.
Пример. Решить дифф. уравнение .
Пример. Решить дифференциальное уравнение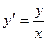 
.
Пример. Решить уравнение .
Пример. Решить уравнение .
Пример. Решить линейное уравнение .
Лекция № 7.
Пример. Решить уравнение 2 порядка .
Пример. Решить уравнение 3 порядка .
Пример.Решить уравнение .
Пример.Решить уравнение .
Пример. Решить уравнение .