Задача с двумя переменными
Графическим способом смогут быть решены задачи линейного программирования с двумя переменными и кое-какие задачи с солидным числом переменных при исполнении определенных условий.
Задача линейного программирования с двумя переменными должна иметь совокупность ограничений, воображающую собой совокупность неравенств. Неравенства смогут быть как вида ? , так и ³ . Условия неотрицательности смогут отсутствовать. Математическая модель должна иметь вид
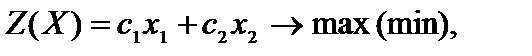 (2.1)
(2.1)
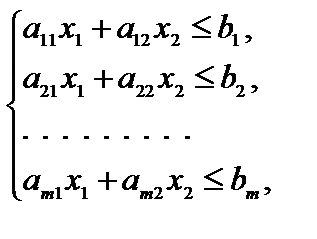 (2.2)
(2.2)
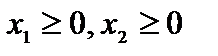 .
.
Способ ответа данной задачи основывается на возможности графического изображения области допустимых ответов (ОДР) и нахождения в данной области оптимального ответа. Для обоснования способа докажем две теоремы.
Теорема 2.1. О виде области ответов линейного неравенства. Областью ответов линейного неравенства 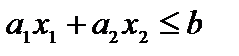 есть одна из двух полуплоскостей, на каковые разбивает всю координатную плоскость
есть одна из двух полуплоскостей, на каковые разбивает всю координатную плоскость 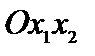 прямая
прямая 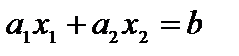 , соответствующая этому неравенству.
, соответствующая этому неравенству.
Подтверждение. В совокупности координат О 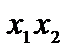 выстроим прямую
выстроим прямую 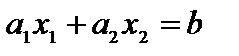 (L) и ее нормаль
(L) и ее нормаль 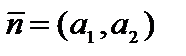 (рис. 2.1).
(рис. 2.1).
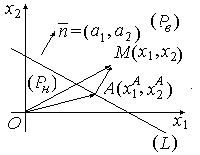
Рис. 2.1
Прямая (L) разбивает плоскость О 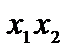 на две полуплоскости: верхнюю (
на две полуплоскости: верхнюю ( 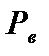 ), соответствующую направлению нормали
), соответствующую направлению нормали 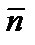 , и нижнюю (
, и нижнюю ( 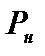 ). Пускай произвольно выбранная точка М(
). Пускай произвольно выбранная точка М( 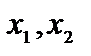 ) в собственности (
) в собственности ( 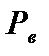 ), ее проекцией на прямую (L) есть точка
), ее проекцией на прямую (L) есть точка 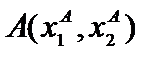 . Вектор
. Вектор 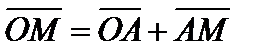 . Координаты векторов
. Координаты векторов 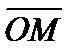 и
и 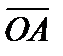 совпадают с координатами точек М и А, т. е.
совпадают с координатами точек М и А, т. е. 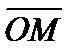 = (
= ( 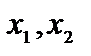 ),
), 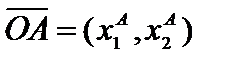 . Вектор
. Вектор 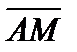 коллинеарен вектору
коллинеарен вектору 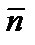 , исходя из этого
, исходя из этого 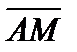 =
= 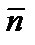 ?l, где l некое число. Отыщем скалярное произведение
?l, где l некое число. Отыщем скалярное произведение 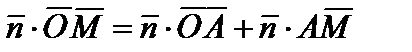 . Запишем это равенство через координаты векторов
. Запишем это равенство через координаты векторов 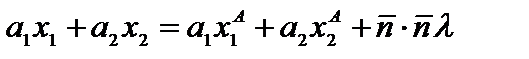 . Так как точка А в собственности прямой (L), то
. Так как точка А в собственности прямой (L), то 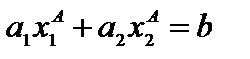 , приобретаем
, приобретаем 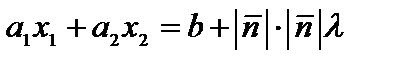 .
.
Из этого следует, что в случае, если l0, т. е. M I( 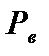 ), то
), то 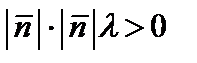 и тогда
и тогда 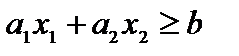 . В случае, если же l ), то
. В случае, если же l ), то 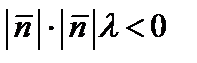 и
и 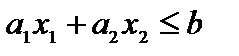 .
.
Пример 2.1. Отыскать область ответов неравенства 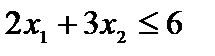 .
.
Ответ. Строим прямую 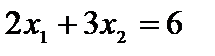 (рис. 2.2).
(рис. 2.2).

Рис. 2.2
Дабы выяснить какая из двух полуплоскостей есть областью ответов, выбираем произвольно пробную точку, не лежащую на прямой, и подставляем ее координаты в неравенство. В случае, если неравенство выполняется, то область, содержащая эту пробную точку, есть областью ответов. В случае, если же неравенство не выполняется, то областью ответов будет полуплоскость, не содержащая пробную точку.
В разглядываемом примере в качестве пробной точки заберём О(0, 0). Подставляем координаты данной точки в неравенство, приобретаем 2 ? 0 + 3 ? 0 ? 6 U 0 ? 6, следовательно, областью ответов есть полуплоскость, содержащая начало координат. Данный факт отмечаем на рисунке стрелками.
В общем случае, в то время, когда совокупность ограничений имеет несколько неравенств, область допустимых ответов (ОДР) находят как пересечение полуплоскостей – ответов каждого из неравенств-ограничений. ОДР возможно безлюдным множеством, многоугольным множеством и многоугольником (многоугольником, неограниченным с одной из сторон). Для нахождения среди допустимых ответов оптимального применяют линии уровня.
Линией уровня именуется прямая, в точках которой целевая функция постоянна Z(X) = 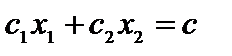 . Уравнение линий уровня
. Уравнение линий уровня
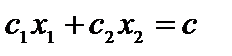 , с = const.
, с = const.
Теорема 2.2. Об трансформации значений функции. Значения целевой функции в точках линий уровня возрастают, в случае, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.

Рис. 2.3
Подтверждение. Пускай целевая функция задачи линейного программирования имеет форму Z(X) = 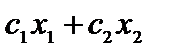 . В совокупности координат О
. В совокупности координат О 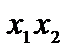 выстроим две линии уровня (L ) и (L ) (рис. 2.3). Их неспециализированная нормаль
выстроим две линии уровня (L ) и (L ) (рис. 2.3). Их неспециализированная нормаль 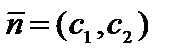 . Пускай точка М(
. Пускай точка М( 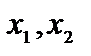 ) I (L ), а точка
) I (L ), а точка 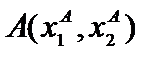 I(L ) есть проекцией М на (L ). Вектор
I(L ) есть проекцией М на (L ). Вектор 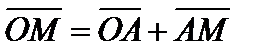 ,
, 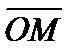 = (
= ( 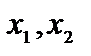 ),
), 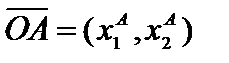 . Так как
. Так как 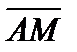 коллинеарен вектору
коллинеарен вектору 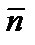 , то вектор
, то вектор 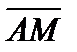 =
= 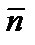 ?l, где l число. Скалярное произведение
?l, где l число. Скалярное произведение 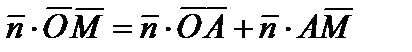 . Применяя координаты векторов
. Применяя координаты векторов 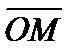 и
и 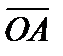 , возможно записать
, возможно записать 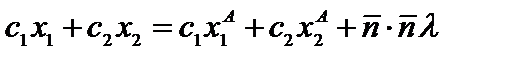 . Так как
. Так как 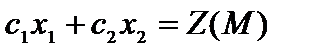 ,
, 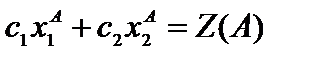 , то
, то 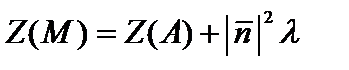 .
.
Из этого приобретаем следующие выводы: 1) в случае, если линия уровня перемещается в направлении нормали 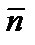 из положения (L ) к (L ), то l 0 и, следовательно,
из положения (L ) к (L ), то l 0 и, следовательно, 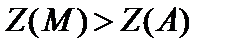 ; 2) в случае, если же линия уровня перемещается в направлении противоположном направлению нормали
; 2) в случае, если же линия уровня перемещается в направлении противоположном направлению нормали 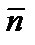 из положения (L ) к (L ), то l 0 и, следовательно,
из положения (L ) к (L ), то l 0 и, следовательно, 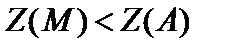 .
.
Так, в случае, если задача линейного программирования на максимум, то для нахождения оптимального ответа линии уровня нужно перемещать по ОДР в направлении нормали, а в задаче на минимум напротив – в противоположном направлении. Для нахождения оптимального ответа задачи нужно применять опорную прямую.
Опорной прямой именуется линия уровня, довольно которой ОДР находится в одной из полуплоскостей и которая имеет хотя бы одну неспециализированную точку с ОДР. В случае, если ОДР есть замкнутым многоугольником, то независимо от вида целевой функции имеется две опорных прямых. В случае, если же ОДР – многоугольное множество (незамкнутый многоугольник), то в зависимости от направления нормали линий уровня ОДР может иметь как две, так и одну опорную прямую.
Метод графического способа ответа задач линейного программирования с двумя переменными содержится в следующем.
1. Строится область допустимых ответов.
2. В случае, если область допустимых ответов есть безлюдным множеством, то ввиду несовместности совокупности ограничений задача не имеет решения.
3. В случае, если область допустимых ответов – это непустое множество, то строится нормаль линий уровня 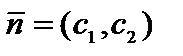 и одна из линий уровня, имеющая неспециализированные точки с данной областью.
и одна из линий уровня, имеющая неспециализированные точки с данной областью.
4. Линия уровня перемещается до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном.
5. В случае, если при перемещении линии уровня по области допустимых ответов в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
6. В случае, если задача линейного программирования имеет оптимальное ответ, то для его нахождения решаются совместно уравнения прямых, ограничивающих область допустимых ответов и имеющих неспециализированные точки с соответствующей опорной прямой. В случае, если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет нескончаемое множество ответов. Хорошим решением есть каждая выпуклая линейная комбинация этих точек. По окончании нахождения оптимальных ответов вычисляется значение целевой функции на этих ответах.
Пример 2.2. Решить задачу линейного программирования
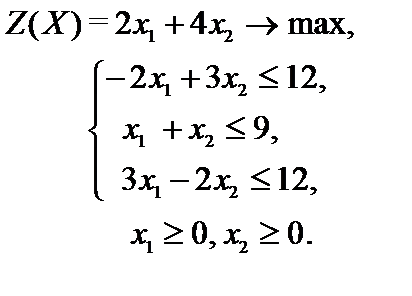
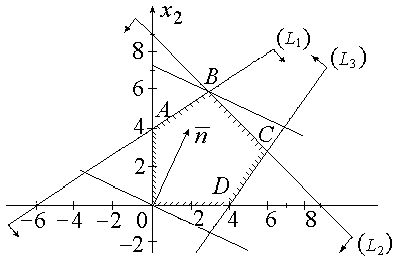
Рис. 2.4
Ответ. Изобразим на плоскости совокупность координат 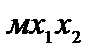 (рис. 2.4) и выстроим граничные прямые области допустимых ответов.
(рис. 2.4) и выстроим граничные прямые области допустимых ответов.
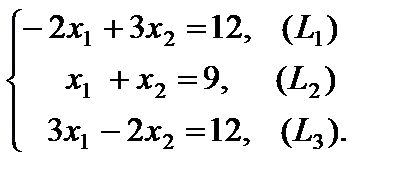
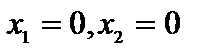
Область допустимых ответов определяется многоугольником ОАВСD. Для линий уровня 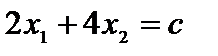 (с = const) строим обычный вектор
(с = const) строим обычный вектор 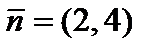 . Перпендикулярно вектору
. Перпендикулярно вектору 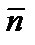 выстроим одну из линий уровня (на рисунке она проходит через начало координат). Так как задача на максимум, то перемещаем ее в направлении вектора
выстроим одну из линий уровня (на рисунке она проходит через начало координат). Так как задача на максимум, то перемещаем ее в направлении вектора 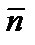 до опорной прямой. На рисунке видно, что опорная прямая проходит через точку B, являющуюся точкой пересечения первой и второй граничных прямых,
до опорной прямой. На рисунке видно, что опорная прямая проходит через точку B, являющуюся точкой пересечения первой и второй граничных прямых, 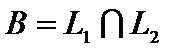 . Для определения координат точки В решаем совокупность уравнений
. Для определения координат точки В решаем совокупность уравнений
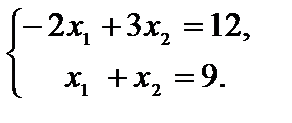
Приобретаем 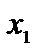 = 3,
= 3, 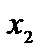 = 6. Данному оптимальному ответу
= 6. Данному оптимальному ответу
X = (3; 6) соответствует большое значение целевой функции
max Z(X) = 2 ? 3 + 4 ? 6 =30.
Ответ: max Z(X) = 30 при X = (3; 6).
Пример 2.3 Решить задачу линейного программирования.
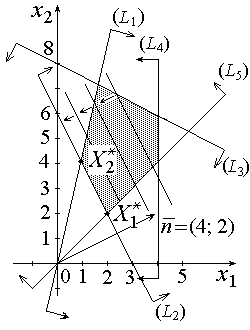
Рис. 2.5
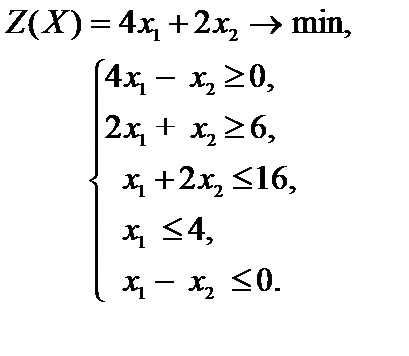

Ответ. Строим область допустимых ответов, нормаль линий уровня 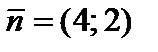 и одну из линий уровня, имеющую неспециализированные точки с данной областью (рис. 2.5). Перемещаем линию уровня в направлении противоположном направлению нормали
и одну из линий уровня, имеющую неспециализированные точки с данной областью (рис. 2.5). Перемещаем линию уровня в направлении противоположном направлению нормали 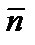 , так как решается задача на отыскание минимума функции. нормаль линии и
, так как решается задача на отыскание минимума функции. нормаль линии и 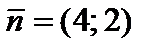 Нормаль уровня
Нормаль уровня 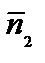 = (2; 1) второй граничной прямой, в направлении которой перемещаются линии уровня, параллельны, поскольку их координаты пропорциональны 4/2 = 2/1. Следовательно, опорная прямая сходится со второй граничной прямой области допустимых ответов, проходит через две угловые точки данной области
= (2; 1) второй граничной прямой, в направлении которой перемещаются линии уровня, параллельны, поскольку их координаты пропорциональны 4/2 = 2/1. Следовательно, опорная прямая сходится со второй граничной прямой области допустимых ответов, проходит через две угловые точки данной области 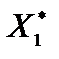 и
и 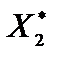 . Задача имеет нескончаемое множество оптимальных ответов, являющихся точками отрезка
. Задача имеет нескончаемое множество оптимальных ответов, являющихся точками отрезка 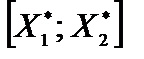 . Находим точки
. Находим точки 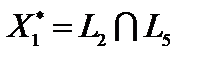 ,
, 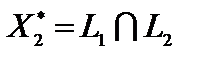 , решая соответствующие совокупности уравнений.
, решая соответствующие совокупности уравнений.
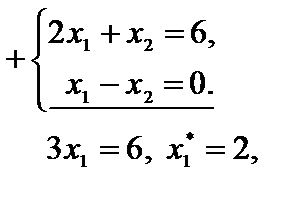
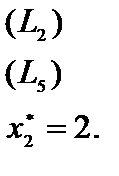
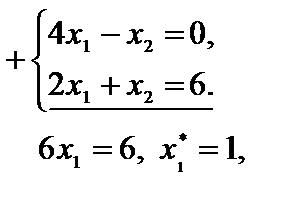
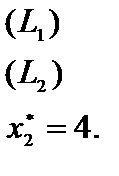
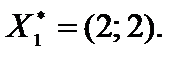
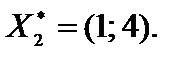
Вычисляем 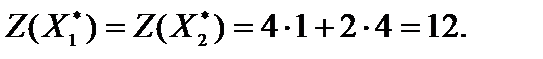
Ответ: 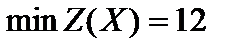 при
при 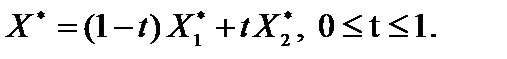
Пример 2.4. Решить задачу линейного программирования.
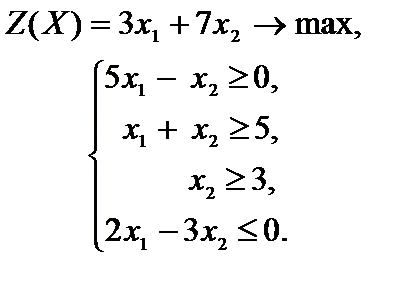
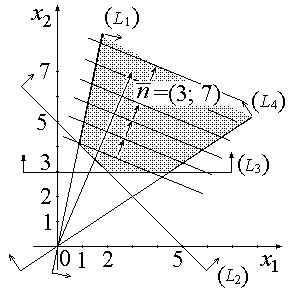
Рис. 2.6
Прямые, ограничивающие ОДР:
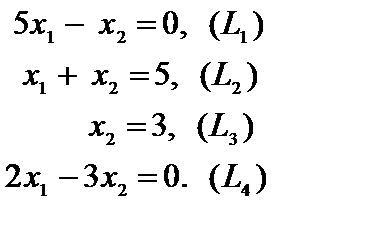
Ответ. Строим область допустимых ответов, нормаль 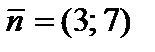 и одну из линий уровня (рис. 2.6). В данной задаче нужно отыскать максимум целевой функции, исходя из этого линию уровня перемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых ответов не ограничена, линия уровня уходит в бесконечность. Задача не имеет решения по обстоятельству неограниченности целевой функции.
и одну из линий уровня (рис. 2.6). В данной задаче нужно отыскать максимум целевой функции, исходя из этого линию уровня перемещаем в направлении нормали. Ввиду того, что в этом направлении область допустимых ответов не ограничена, линия уровня уходит в бесконечность. Задача не имеет решения по обстоятельству неограниченности целевой функции.
Ответ: 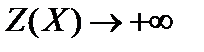 .
.
Пример 2.5. Решить задачу линейного программирования.
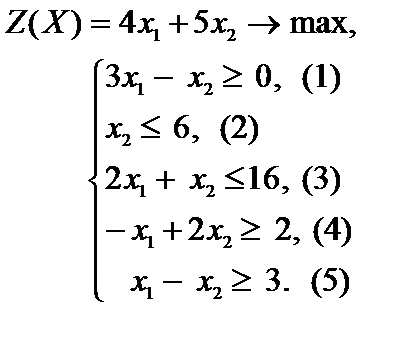
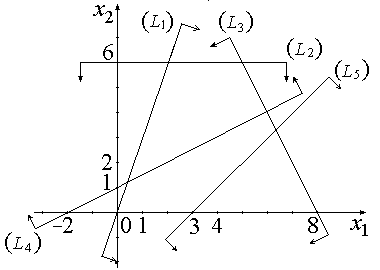
Рис. 2.7
Ответ. Строим прямые линии, соответствующие неравенствам совокупности ограничений и находим полуплоскости, являющиеся областями ответов этих неравенств (рис. 2.7). Область допустимых ответов задачи – безлюдное множество. Задача не имеет решения ввиду несовместности совокупности ограничений.
Ответ: совокупность ограничений несовместна.
Лекция №3 ГРАФИЧЕСКИЙ СПОСОБ Ответа ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Графический способ ответа задач линейного
программирования с n переменными
Данным способом решаются задачи линейного программирования, имеющие каноническую форму и удовлетворяющие условию 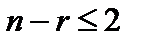 , где n – число малоизвестных совокупности, r – ранг совокупности векторов-условий (число линейно свободных уравнений совокупности). В случае, если уравнения совокупности ограничений линейно свободные, то r = m.
, где n – число малоизвестных совокупности, r – ранг совокупности векторов-условий (число линейно свободных уравнений совокупности). В случае, если уравнения совокупности ограничений линейно свободные, то r = m.
Разглядим метод способа на конкретном примере.
Пример 2.6. Решить графическим способом.
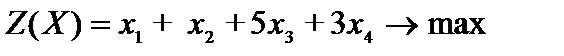 ,
,
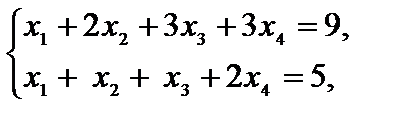
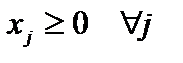 .
.
Ответ.
1. Контролируем условие применимости графического способа. Нетрудно видеть, что каждые два из векторов-столбцов совокупности ограничений, к примеру, 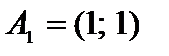 ,
, 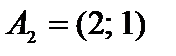 являются линейно свободными, поскольку их координаты непропорциональны, исходя из этого ранг совокупности векторов-условий r = 2. Находим n — r = 4 — 2 =2 ? 2. Следовательно, способ применим.
являются линейно свободными, поскольку их координаты непропорциональны, исходя из этого ранг совокупности векторов-условий r = 2. Находим n — r = 4 — 2 =2 ? 2. Следовательно, способ применим.
2. Приведем совокупность ограничений-уравнений к равносильной, разрешенной посредством способа Жордана – Гаусса. В один момент исключим разрешенные малоизвестные из целевой функции. Для этого
Т а б л и ц а 2.1
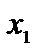
|
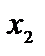
|
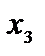
|
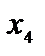
|
b |
| –5 | ||||
| –1 | ||||
| –5 |
запишем коэффициенты целевой функции в последней (третьей) строке таблицы, под матрицей совокупности. Вычисления приведены в табл. 2.1. Задача по окончании совершённых преобразований
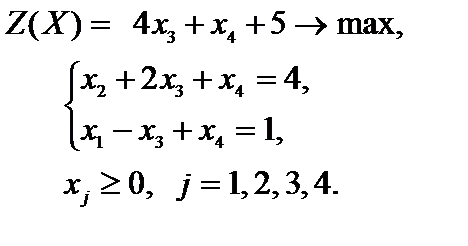
3. Отбросим в уравнениях-ограничениях неотрицательные разрешенные малоизвестные 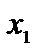 и
и 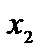 и заменим символы равенства символами
и заменим символы равенства символами 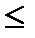 , возьмём эквивалентную задачу линейного программирования с двумя переменными
, возьмём эквивалентную задачу линейного программирования с двумя переменными
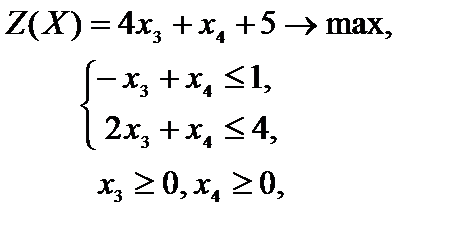

которая решается графическим способом (рис. 2.8).
Рис. 2.8
Оптимальное ответ 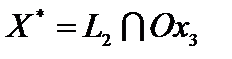 ;
; 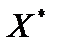 = (2; 0). Значение целевой функции
= (2; 0). Значение целевой функции 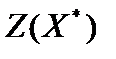 = 4 ? 2 + 0 + 5 = 13.
= 4 ? 2 + 0 + 5 = 13.
4. Используем совокупность ограничений исходной задачи, приведенную к каноническому виду,
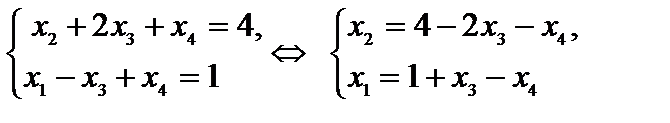
и оптимальное ответ задачи с двумя переменными 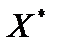 = (2; 0) для нахождения оптимального ответа исходной задачи
= (2; 0) для нахождения оптимального ответа исходной задачи
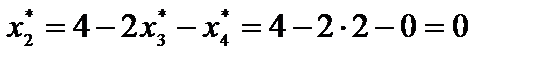 ;
;
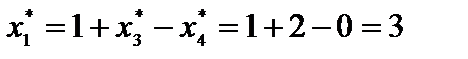 .
.
Записываем оптимальное ответ исходной задачи
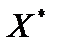 = (3; 0; 2; 0). Значение целевой функции на оптимальном ответе сходится со значением целевой функции для запасного задачи
= (3; 0; 2; 0). Значение целевой функции на оптимальном ответе сходится со значением целевой функции для запасного задачи 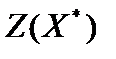 = 1 ? 3 + 2 ? 0 + 5 ? 2 + 3 ? 0 = 13.
= 1 ? 3 + 2 ? 0 + 5 ? 2 + 3 ? 0 = 13.
Ответ: max Z(X) = 13 при 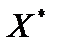 = (3; 0; 2; 0).
= (3; 0; 2; 0).
Задания для независимого ответа
Решить задачи линейного программирования графическим способом.
Пример 2.7. 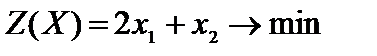 ,
,
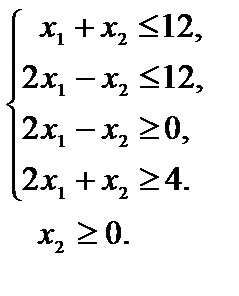
Пример 2.8. 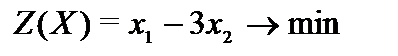 ,
,
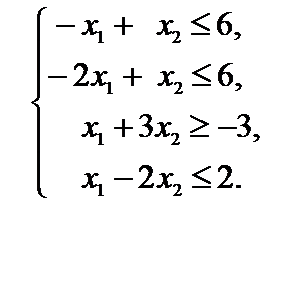
Пример 2.9. 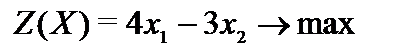 ,
,
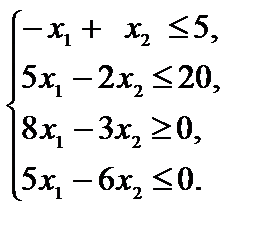
Пример 2.10. 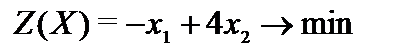 ,
,
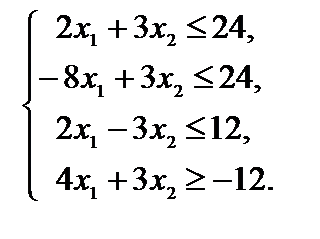
Пример 2.11. 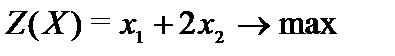 ,
,
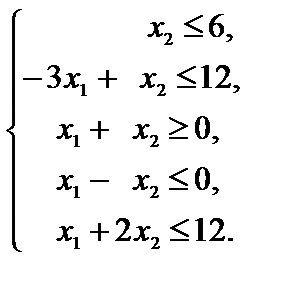
Пример 2.12. 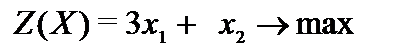 ,
,
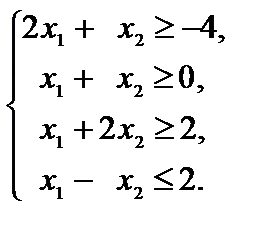
Лекция№4. СВОЙСТВА ОТВЕТОВ ЗАДАЧ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ