Ранее рассматривались догадки, в которых закон распределения главной совокупности предполагался известным. Сейчас займемся проверкой догадок о предполагаемом законе малоизвестного распределения, другими словами будем контролировать нулевую догадку о том, что главная совокупность распределена по некоему известному закону. В большинстве случаев статистические параметры для проверки таких догадок именуются параметрами согласия.
Критерием согласия именуется критерий проверки догадки о предполагаемом законе малоизвестного распределения. Это численная мера расхождения между эмпирическим и теоретическим распределением.
Главная задача.Дано эмпирическое распределение (выборка). Сделать предположение (выдвинуть догадку) о виде теоретического распределения и проверить выдвинутую догадку на заданном уровне значимости ?.
Ответ главной задачи складывается из двух частей:
1. Выдвижение догадки.
2. Проверка догадки на заданном уровне значимости.
Разглядим детально эти части.
1. Выбор гипотезыо виде теоретического распределения комфортно делать посредством полигонов либо гистограмм частот. Сравнивают эмпирический полигон (либо гистограмму) с известными законами распределения и выбирают самый подходящий.
Приведём графики наиболее значимых законов распределения:
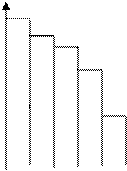
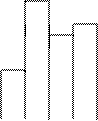
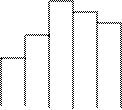
Примеры эмпирических законов распределения приведены на картинках:
 |
|||||||||
 |
|||||||||
 |
|||||||||
а) б) в)
При (а) выдвигается догадка о обычном распределении, при (б) — догадка о равномерном распределении, при (в) — догадка о распределении Пуассона.
Основанием для выдвижения догадки о теоретическом распределении смогут быть теоретические предпосылки о характере трансформации показателя. К примеру, исполнение условий теоремы Ляпунова разрешает сделать догадку о обычном распределении. Равенство средней и дисперсии наводит на догадку о распределении Пуассона.
На практике значительно чаще приходится видеться с обычным распределением, исходя из этого в отечественных задачах требуется проверить лишь догадку о обычном распределении.
Проверка догадки о теоретическом распределении отвечает на вопрос: возможно ли вычислять расхождение между предполагаемыми теоретическим и эмпирическим распределениями случайным, несущественным, растолковываемым случайностью попадания в выборку тех либо иных объектов, либо же это расхождение говорит о значительном расхождении между распределениями. Для проверки существуют разные способы (критерии согласия) — c2 (хи-квадрат), Колмогорова, Романовского и др.
Критерий Пирсона.
Преимуществом критерия Пирсона есть его универсальность: с его помощью возможно контролировать догадки о разных законах распределения.
1. Проверка догадки о обычном распределении.Пускай взята выборка большого количества п с громадным числом разных значений вариант. Для удобства ее обработки поделим промежуток от мельчайшего до громаднейшего из значений вариант на s равных частей и будем вычислять, что значения вариант, попавших в любой промежуток, приближенно равны числу, задающему середину промежутка. Подсчитав число вариант, попавших в любой промежуток, составим так именуемую сгруппированную выборку:
варианты………..х1 х2 … хs
частоты………….п1 п2 … пs ,
где хi – значения середин промежутков, а пi – число вариант, попавших в i-й промежуток (эмпирические частоты). По взятым разрешённым можно вычислить выборочное и выборочное среднее квадратическое отклонение ?В. Удостоверимся в надежности предположение, что главная совокупность распределена по обычному закону с параметрами M(X) = , D(X) = . Тогда возможно отыскать количество чисел из выборки количества п, которое должно появляться в каждом промежутке наряду с этим предположении (другими словами теоретические частоты). Для этого по таблице значений функции Лапласа отыщем возможность попадания в i-й промежуток:
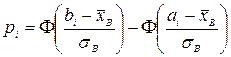 ,
,
где аi и bi — границы i-го промежутка. Умножив полученные возможности на количество выборки п, отыщем теоретические частоты: пi =n?pi.Отечественная цель – сравнить эмпирические и теоретические частоты, каковые, само собой разумеется, отличаются друг от друга, и узнать, являются ли эти различия несущественными, не опровергающими догадку о обычном распределении исследуемой случайной величины, либо они так громадны, что противоречат данной догадке. Для этого употребляется критерий в виде случайной величины
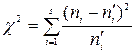 . (7)
. (7)
Суть ее очевиден: суммируются части, каковые квадраты отклонений эмпирических частот от теоретических составляют от соответствующих теоретических частот. Возможно доказать, что независимо от настоящего закона распределения главной совокупности закон распределения случайной величины (7) при пытается к закону распределения с числом степеней свободы k = s – 1 – r, где r – число параметров предполагаемого распределения, оцененных согласно данным выборки. Обычное распределение характеризуется двумя параметрами, исходя из этого k = s – 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием
(8)
где ? – уровень значимости. Следовательно, критическая область задается неравенством а область принятия догадки — .
Итак, для проверки нулевой догадки Н0: главная совокупность распределена нормально – необходимо вычислить по выборке замечаемое значение критерия:
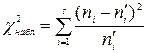 , (7`)
, (7`)
а по таблице критических точек распределения ?2 отыскать критическую точку , применяя узнаваемые значения ? и k = s – 3. В случае, если — нулевую догадку принимают, при ее отвергают.
Пример. Результаты изучения спроса на товар представлены в таблице:
| Цена, руб. | 120–160 | 160–180 | 180–200 | 200–220 | 220–280 |
| Кол-во, шт. |
Выдвинуть догадку о виде распределения и проверить её на уровне значимости a=0,01.
I. Выдвижение догадки.
Для указания вида эмпирического распределения выстроим гистограмму
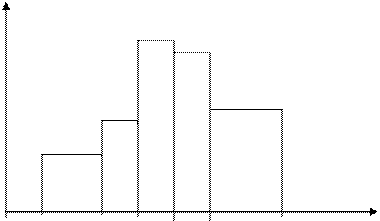 |
120 160 180 200 220 280
По виду гистограммы возможно сделать предположение о обычном законе распределения изучаемого показателя в главной совокупности.
II. Удостоверимся в надежности выдвинутую догадку о обычном распределении, применяя критерий согласия Пирсона.
1. Вычисляем , sВ.В качестве вариант заберём среднее арифметическое финишей промежутков:
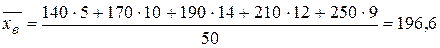 ;
;
.
2. Отыщем промежутки (Zi; Zi+1): 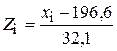 ;
; 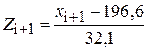 .
.
За левый финиш первого промежутка примем (-¥), а за правый финиш последнего промежутка — (+¥). Результаты представлены в табл. 4.
3. Отыщем теоретические возможности Рi и теоретические частоты (см. табл. 4).
Таблица 4
4. Сравним эмпирические и теоретические частоты. Для этого:
а) вычислим замечаемое значение критерия Пирсона.
Вычисления представлены в табл.5.
Таблица 5
| i | |||||
| 6,36 | -1,36 | 1,8496 | 0,291 | ||
| 8,72 | 1,28 | 1,6384 | 0,188 | ||
| 12,12 | 1,88 | 3,5344 | 0,292 | ||
| 11,18 | 0,82 | 0,6724 | 0,060 | ||
| 11,64 | -2,64 | 6,9696 | 0,599 | ||
| S |
б) по таблице критических точек распределения c2 при заданном уровне значимости a=0,01 и числе степеней свободы k=m–3=5–3=2 находим критическую точку ; имеем .
Сопоставляем c . . Следовательно, нет оснований отвергать догадку о обычном законе распределения изучаемого показателя главной совокупности. Т.е. расхождение между эмпирическими и теоретическими частотами незначимо (случайно).
Замечание. Промежутки, которые содержат маленькие эмпирические частоты (ni
Пример. По выборке из 24 вариант выдвинута догадка о обычном распределении главной совокупности. Применяя критерий Пирсона при уровне значимости среди заданных значений = {34, 35, 36, 37, 38} указать: а) громаднейшее, для которого нет оснований отвергать догадку; б) мельчайшее, начиная с которого догадка должна быть отвергнута.
Отыщем число степеней свободы посредством формулы:
,
где — число групп выборки (вариант), — число параметров распределения.
Так как обычное распределение имеет 2 параметра ( и ), приобретаем
.
По таблице критических точек распределения , по числу степеней и заданному уровню значимости свободы определяем критическую точку .
При а) для значений , равных 34 и 35, нет оснований отвергать догадку о обычном распределении, поскольку . А громаднейшее среди этих значений .
При б) для значений 36, 37, 38 догадку отвергают, поскольку . Мельчайшее среди них .
2. Проверка догадки о равномерном распределении. При применении критерия Пирсона для проверки догадки о равномерном распределении главной совокупности с предполагаемой плотностью возможности
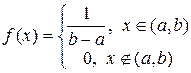
нужно, вычислив по имеющейся выборке значение , оценить параметры а и b по формулам:
, (9)
где а* и b* — оценки а и b. Вправду, для равномерного распределения М(Х) = 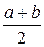 ,
, 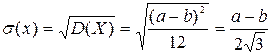 , откуда возможно взять совокупность для определения а* и b*:
, откуда возможно взять совокупность для определения а* и b*: 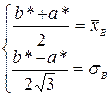 , ответом которой являются выражения (9).
, ответом которой являются выражения (9).
После этого, предполагая, что 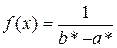 , возможно отыскать теоретические частоты по формулам
, возможно отыскать теоретические частоты по формулам
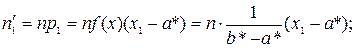
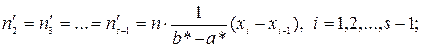
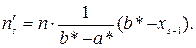
Тут s – число промежутков, на каковые разбита выборка.
Замечаемое значение критерия Пирсона вычисляется по формуле (7`), а критическое – по таблице с учетом того, что число степеней свободы k = s – 3. Затем границы критической области определяются равно как и для проверки догадки о обычном распределении.
3. Проверка догадки о показательном распределении.В этом случае, разбив имеющуюся выборку на равные по длине промежутки, разглядим последовательность вариант 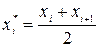 , равноотстоящих друг от друга (думаем, что все варианты, попавшие в i – й промежуток, принимают значение, совпадающее с его серединой), и соответствующих им частот ni (число вариант выборки, попавших в i – й промежуток). Вычислим согласно этой информации и примем в качестве оценки параметра ? величину
, равноотстоящих друг от друга (думаем, что все варианты, попавшие в i – й промежуток, принимают значение, совпадающее с его серединой), и соответствующих им частот ni (число вариант выборки, попавших в i – й промежуток). Вычислим согласно этой информации и примем в качестве оценки параметра ? величину 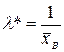 . Тогда теоретические частоты вычисляются по формуле
. Тогда теоретические частоты вычисляются по формуле
После этого сравниваются замечаемое и критическое значение критерия Пирсона с учетом того, что число степеней свободы k = s – 2.
Пример. Для выборки, интервальный статистический последовательность которой имеет форму
| Номер промежутка | Границы промежутка | Эмпирические частоты |
| 2 – 5 | ||
| 5 – 8 | ||
| 8 – 11 | ||
| 11 – 14 | ||
| 14 – 17 | ||
| 17 – 20 |
проверить при уровне значимости ? = 0,05 догадку о:
а) показательном; б) равномерном; в) обычном законе распределения главной совокупности посредством критерия Пирсона.
Количество выборки п = 70. Будем вычислять вариантами середины частичных промежутков: х1 = 3,5, х2 = 6,5,…, х6 = 18,5.
Отыщем = 11,43; ?В = 4,03; s = 4,05.
а) Вычислим теоретические частоты в предположении о показательном распределении главной совокупности при 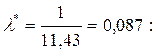
подобно Замечаемое значение критерия 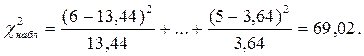 Критическая точка ?2(0,05;4)=9,5; и догадка о показательном распределении отклоняется.
Критическая точка ?2(0,05;4)=9,5; и догадка о показательном распределении отклоняется.
б) Для равномерного распределения
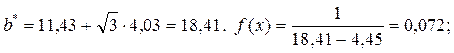 теоретические частоты: Замечаемое значение критерия
теоретические частоты: Замечаемое значение критерия  гипотеза и Критическая точка о равномерном распределении отклоняется.
гипотеза и Критическая точка о равномерном распределении отклоняется.
в) Теоретические частоты для обычного распределения:
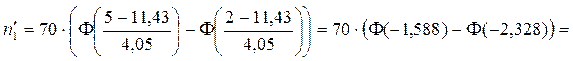
Так же вычисляются Замечаемое значение критерия 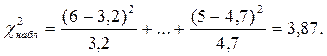 Критическая точка Потому, что догадка о обычном распределении главной совокупности принимается.
Критическая точка Потому, что догадка о обычном распределении главной совокупности принимается.
Критерий Колмогорова.
Данный критерий используется для проверки несложной догадки Н0 о том, что свободные одинаково распределенные случайные размеры Х1, Х2, …, Хп имеют заданную постоянную функцию распределения F(x).
Отыщем функцию эмпирического распределения Fn(x) и будем искать границы двусторонней критической области, определяемой условием
. (10)
А.Н.Колмогоров доказал, что при справедливости догадки Н0 распределение статистики Dn не зависит от функции F(x), и при
где 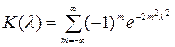 — (11)
— (11)
— критерий Колмогорова, значения которого возможно отыскать в соответствующих таблицах. Критическое значение критерия ?п(?) вычисляется по заданному уровню значимости ? как корень уравнения .
Возможно продемонстрировать, что приближенное значение вычисляется по формуле
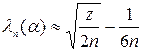 , где z – корень уравнения
, где z – корень уравнения 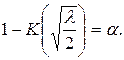
На практике для вычисления значения статистики Dn употребляется то, что
, где 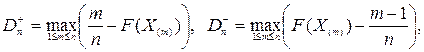
а — вариационный последовательность, выстроенный по выборке Х1, Х2, …, Хп. Возможно дать следующее геометрическое истолкование критерия Колмогорова: в случае, если изобразить на плоскости Оху графики функций Fn(x), Fn(x) ±?n(?) (рис. 1), то догадка Н0 верна, в случае, если график функции F(x) не выходит за пределы области, лежащей между графиками функций Fn(x) -?на данный момент(?) и Fn(x) +?n(?).