То, что сделано, именуется сближением либо рядом размещением. Соединение, а тем более слияние, отсутствует по той причине, оно еще не введено в конструкцию. Вводя слияние как противоположность разделению, возвращаемся к конструкции рис 2 (рис. 11).
|
Рис. 11
Из рассмотрения вышеизложенного приобретаем следствие: Мир, что видится дискретным, складывающимся из отдельных тел, таковым не есть. В нем присутствует еще одно уровень качества, противоположное дискретности — сплошность. Причем роль этих качеств разна:
дискретность делает мир узнаваемым, разрешая в определенной степени вычленять из мира тела и разглядывать их как отдельные объекты и, в первую очередь, вычленять из мира себя (Я и все другое).
сплошность делает мир целым, телесным, снабжая его существование, как и всего, что имеется, так и того, чего нет, т.е. нам малоизвестного. И, следовательно, никак не может быть воспринят дискретным (отдельным). В сплошности (непрерывности) «отдельное» отсутствует.
Самое поразительное, что сплошность мира люди, в особенности связанные с наукой, принимают как вакуум, как отсутствие всего, другими словами бестелесное, что объяснимо, т.к. диалектические понятия «все» и «ничто» равнозначны (равноправны).
1.3. Введение в диалектику математических
понятий
Разглядим понятия, которые связаны с геометрией. Самое популярное определение понятия «геометрия» приводится в кожный покров1]:
«… часть математики, изучающая формы и пространственные отношения, и формы и другие отношения, схожие с пространственными по собственной структуре».
В данной формулировке объект «геометрия» обобщается словами «формы и пространственные отношения». Начнем с формы.
Форма как наружный вид, внешние очертания либо конфигурация дешева всем, потому, что отождествляется с поверхностью тела. Последняя, со своей стороны, есть границей, разрешающей заметить либо иным образом почувствовать отдельность тела. К примеру, выражение «тело по форме напоминающее шар» ясно всем как наименование сферически замкнутой поверхности. Тело, отображаемое в собственной форме, может двигаться (нефиксируемое самодвижение), или покоиться (оставаться довольно неподвижным), или изменяться (деформироваться). механическое изменение и Самодвижение формы в любой момент связано с движением и взаимодействием. Так, геометрия, изучая форму предметов, кроме статики неявным образом соприкасается не только с математическим, но и с механическим перемещением, т.е. с физикой. Другое дело, знают ли это математики либо наличие фактора перемещения в геометрии ускользает от их внимания.
Весьма значительно для понимания то, что форма это не независимое уровень качества тел, а следствие отдельности, ее проявление. Отдельность, со своей стороны, следствие общей дискретности, которая фиксируется в отечественном мире. Одновременно с этим отдельность (единичность) это отношение двух: объекта и субъекта, которое в совокупности образует еще одно уровень качества — пространственность (как протяженность). И потому: не может быть для того чтобы начального состояния, как наличие безлюдного пространства (пустоты) и тела (безразлично субъекта либо объекта). Субъект чувствует и поймёт собственную отдельность, в случае, если его органы эмоций зафиксируют что-то, что не есть им (не в собственности ему), т.е. отделено от него некоторым расстоянием — пространством. (Существование пространства — имеется отрицание тела, имеется показатель его формальной конечности, имеется переход от тела к его противоположности, к телесности другого качества.)
Пространственные отношения кроме того по собственному характеру предполагают как наличие перемещения (потому, что для определения расстояния нужны движение и эталоны), так и пропорциональность взаимоотношений изменяемых форм. Перемещение обусловливается следующими факторами — особенностями пространства:
пространство это то, что снабжает возможность перемещения тел (механического перемещения любого вида, включая пульсацию);
отношение в любой момент имеется сотрудничество как минимум двух объектов и, следовательно, пространственные отношения, по сути, имеется отношения тел при помощи собственных параметров. Исходя из этого, исследуя пространство, мы неизбежно и также в неявной форме вводим в него тела, и потому пространство делается промежутком между телами. И лишь игнорирование перемещения в мысленном представлении пространства обусловливает свойству «пространство» качества субстанции равнозначной материи.
Само наличие пространства фиксируется лишь методом перемещения тел и, следовательно, где нет перемещения, в том месте нет и пространства, как нет и самой материи. Так в полной темноте, перед тем как сделать ход, человек протягивает вперед руку (вводит тело в пространство), убеждается в присутствии оного, а после этого вводит в него и собственный тело. Потом операция повторяется, пока рука не упирается в стенку (отсутствие пространства). Так, появляется понятие размеров пространства (количество шагов). Пребывав в неподвижности и в полной темноте, запрещено ничего сообщить о пространстве ни как о пустоте, ни как об отношении.
Появляется вопрос: что же такое пространство? Вот вероятные варианты ответов:
Ответ А: Это ничем не заполненная пустота (безлюдной ящик без стенок). Другими словами тождеством:
пространство = пустота = отсутствие всего,
постулируется превращение пространства в непознаваемое. В вещь в себе. Появление в таком мысленном пространстве субъекта нереально по определению, а без субъекта кто будет познавать? Да и познавать-то нечего (ничего нет).
Ответ Б: Пространство имеется то, что окружает каждое тело как повторение его жёсткой формы (скажем как воздушная оболочка Почвы) и не владеет твердостью, мешающей сближению тел. Данный ответ переводит пространство в объект изучения физики.
Ответ В: Пространство имеется телесная протяженность между макротелами, грамотный протяженностью микротел (эфиром), что обусловливает макрообъектам возможность перемещения, сохраняя наряду с этим видимость их отдельности. Данный ответ образует мостик между геометрией и физикой. Физики, изучая их свойства и тела, будут учитывать закономерности вещественного пространства (эфира), а математики, трудясь с кажущейся пустотой, не забывают, что она имеет телесность и протяжённость.
Резюме: Современная геометрия, изучающая формы тел, постоянно имеет дело со статикой (неподвижными поверхностями тел). Возможно представить, как геометры «ползают» по поверхности, оставляя следы: как точки (в то время, когда они стоят); как линии (в то время, когда они измеряют поверхность); как плоскости (в то время, когда они рисуют «карты» этих поверхностей). Для понимания предмета геометрии это весьма значительно, потому, что все операции на плоскости требуют неявного нахождения на ней и геометра, хотя бы в виде точки, владеющей свойством двигаться.
В то время, когда начинается процесс трансформации формы (поверхности), геометры удирают (улетают) «чтобы не было» и возвращаются на плоскость только тогда, в то время, когда процесс деформации закончен, т.е. в статику. Это сущность статической геометрии. Дабы знать, как изменяется форма, т.е. видеть процесс, геометр обязан, хотя бы в воображении стать участником процесса, правильнее, его исполнителем, и учитывать вещественность процесса, что нереально в статической геометрии. В этом случае геометр (исполнитель) в любой момент центр, а инструмент (идея) выполняет роль измерителя, фиксирующего процесс, и геометрия выходит за рамки статики. Но продолжим определения [1]:
2) «Начальные понятия геометрии появились в следствии отвлечения от отношений тел и всяких свойств, не считая величины и взаимного расположения. Первое выражается в прикосновении либо прилегании тел друг к другу, в том, что одно тело имеется часть другого, в размещении «между», «в» и т.п. Второе видится в понятиях «больше», «меньше», в понятии о «равенстве тел».
3) «Геометрическое тело имеется абстракция, в которой сохраняются только размеры и форма в полном отвлечении от всех других особенностей».
В формулировках 2 и 3 имеются определенные недоговоренности, если не сообщить большего:
а) Отвлечение от отношений и всяких свойств абсолютно отрывает геометрические тела от настоящих объектов, не оставляя им никаких природных качеств и тем самым превращая их в пустую абстракцию, ничем не связанную с действительностью;
б) Обсуждаются и определяются лишь тела, а также вводится и понятие «геометрическое тело». Все это — рассмотрение формы. А в это же время и в этом, и в других определениях исчезает представление о пространстве, которое геометрия обязуется изучать по определению.
в) Строго подходя к определению, понятие «геометрическое тело» получено при помощи содержания и разделения формы, в то время как ранее отмечалось, что форма имеется только проявление содержания, т.е. материальности тела. Аналогом таковой абстракции может служить мир мыльных пузырей, где то, что находится вне пузырей и внутри их, тождественно (однородно).
г) Введение в начальное понятие количества, кроме того в несложной форме (больше, меньше), равнозначно присутствию «свободного» наблюдателя, что и являет собой эталон и ?либо эквивалентно нанесению на пространство твёрдой координатной (размерной) сетки.
д) Вместе с тем термин «пространственные отношения» имеется недоговоренность, т.к. под отношениями подразумевают отношение тел.
Так, предметом геометрии являются формы, абстрагированные от объектов окружающего мира, среди них и от пространства и, следовательно, в статической геометрии пространство отсутствует по определению.
Остановимся на некоторых гносеологических качествах этого абстрагирования, каковые в той либо второй мере находят отображение в математике и в частности в геометрии. Начнем с несложных количественных и качественных операций, потому, что «уровень качества» неотъемлемая категория любой науки и а также математики. Разглядим задачку, которую психиатры предлагают время от времени детям младшего школьного возраста для определения их способности мыслить абстрактно:
«Сколько будет в случае, если к одной корове прибавить одну лошадь?»
Считается, что верный ответ — два животных, и делается вывод, что ребенок может мыслить абстрактно (может обобщать понятия). Но так ли это?
Посмотрим, какая логика определяет данный ответ:
а) предполагается
1 корова = 1 животное,
1 лошадь = 1 животное,
из этого 1 корова = 1 лошади и, складывая, приобретаем
1 лошадь + 1 корова = 2 животных.
Кому как, а для нас эта операция непостижима. Непостижима по причине того, что складываются не лошадь и корова, а формальные классы, не воображающие определенного качества, сложение которых есть полной бессмыслицей и для математики, и для практики. (Дети это замечательно ощущают и потому стесняются приобретать тот ответ, что устраивает психологов.)
Рассуждать приходится по иному.
Понятие «корова» индивидуальность (тело), понятие «лошадь» также индивидуальность (также тело). И дабы их сложить нужно индивидуальности обезличить, перевоплотить в бескачественные, но существующие телесные объекты, в мысленные конструкции.
Следовательно, абстрагирование как переход к второму качеству содержится не в том, что вводится понятие, отвлеченное от действительности, а в том, что итог абстрагирования отрицает существование прошлого качества объекта, ненадобность этого качества для данной формализации. Происходит подмена объекта в мышлении его «потребительским» качеством. Сам объект наряду с этим остается неизменным, употребляется лишь вторая его данность. Это очень важная формальная операция. Абстрагирование от объекта не создаёт замены объекта его схематическим отображением, а изменяет качественную составляющую данного объекта, концентрирует внимание на втором качестве, которое делается главным при проведении некоей формальной (к примеру, математической) операции, и исходя из этого математика делается не столько количественной, сколько качественной наукой. Но эта качественность математического знания на сегодня не замечается.
б) пускай удалось выполнить операцию а), т.е. настоящие объекты (живые существа) перевоплотить в однообразные мысленные конструкции, именуемые Y, тогда:
Вариант 1 ? 1Y + 1Y = Y(1 + 1) = 2Y — это одна возможность,
Вариант 2 ? Y + Y = YY — это вторая возможность.
Вариант 2 возможно записать в противном случае, в случае, если «слить» YY в единое ? «в два раза» большее прошлого:
Y + Y = ? .
В варианте 2 наличествуют лишь абстрактные объекты Y (знаки объектов – отдельности), символ + это разместить рядом, сохранив тем самым различие не только в памяти, но и визуально. Операция рядом размещения не есть математической операцией. Изображение ? — уже математическая операция, обусловливающая в следствии сложения происхождение нового качества.
Появление ? ведет к исчезновению Y и Y, а в варианте 1 отпадает необходимость в качестве Y, которое, возможно сократить, подразумевая наряду с этим, что складываются не обнажённые числа, а отображения однообразных качеств этих чисел:
1Y + 1Y = Y(1 + 1) = 2Y
1 + 1 = 2 .
Сокращение Y как бы по большому счету убирает в уравнении качественную составляющую (животное) и отображает его уже не как животное, а как тело, т.е. как целое. И любая цифра в последнем уравнении есть нерасчленимым, отдельным целым. И в данном примере наличествует не абстрагирование от объекта к количественной величине, а напротив, сохранение каждого объекта (как целого с качествами определенной, но формальной отдельности). Неосознанно мы, как детишки дошкольники, говорим в уме: одно и одно тело равняется двум телам, другими словами двум целым.
Возможно разглядывать символ + как метод слияния и тогда:
+ = = — а это один объект
Т. е. при слиянии 1 + 1 = 1 — как единое целое появился новый объект, а ветхие объекты как целое провалились сквозь землю, не смотря на то, что они и присутствуют в уравнении и в отечественной памяти. Это фиксация в отечественной памяти и в уравнении предшествующего момента (левой части), которая уже «отмерла», уже отсутствует и потому небытийная. Практически, с возникновением правой части, левая часть исчезает. Она собственную роль выполнила, и для нее уже нет места в новом времени и пространстве. Этого требует сама природа, потому, что в реальности все места заняты и появление нового допустимо лишь при исчезновении ветхого.
Данное положение диалектики слабо усваивается не только математиками, но и философами. Не смотря на то, что в быту любой из нас с этими процессами сталкивается повседневно. К примеру: в сосуд с водой возможно влить молоко, лишь вылив воду. И в то время, когда эта операция проделана, то любой снова вошедший в помещение (не видевший процесса выливания воды и наливания молока) заметит сосуд с молоком, и лишь субъект, проделавший эту операцию, будет не забывать, что перед тем в нем была вода. Конкретно подобная память и сохраняется в левой части рассмотренных уравнений. Собственного рода «замороженная» память.
Итак, все замыкается на людской мышлении, на абстрагировании и в один момент на памяти о предшествующем. Память — попытка перевоплотить дискретное в постоянное, другими словами возвратиться в действительность, как в последовательную череду событий. Любое природное явление (событие) протекающее во времени для памяти — это необычный кинопроектор, движущийся с регулируемой скоростью ленты. Медлительно — и мы видим прерывистость, скоро — и все медлено и непрерывно. В случае, если же взглянуть кадры на пленке — так перемещение по большому счету отсутствует. И в данной картине мы упираемся в весьма занимательную двойственность, имеющую место и в математике: в покой и движение.
На бытовом уровне мы фиксируем перемещение как перемещение довольно некоего неподвижного объекта и легко находим как то, так и второе. И в случае, если выдвигается положение о том, что перемещение есть атрибутом материи, без наличия которого материя не существует, то существование для того чтобы атрибута должно обусловливать и наличие противоположного качества — неподвижности и как следствие существования этого качества — отсутствие материи, отображаемое словом «ничто». И это диалектично, так когда ничто может уравновесить все и в единстве снабжать существование того явления, которое и именуется словом — целое.
Но не будем отвлекаться и возвратимся к базам геометрии, возвратимся к форме.
Так что же такое форма? Форма — отграниченность, создающая отдельность. Это свойство, разрешающее нам заметить (выделить из мира) любой объект (тело, предмет, вещь и т.д.). К примеру, мы наблюдаем в ясный летний сутки на небо, на котором нет ни одного облачка. И что же мы видим? Мы видим чистое небо. Как приходит такое познание? Оно обуславливается границей. Вот поверхность Почвы, а дальше воздушное пространство, что невидим, но его толща, освещаемая Солнцем, получает голубоватый оттенок, и эту голубизну воздуха мы именуем небом. Что еще возможно заметить на небе? Ничего, пока не покажутся облака, каковые видны через отграниченность белого от голубого. Ответ делается неоднозначным:
а) Я вижу небо с тучами.
б) Я вижу облака на небе.
в) Я вижу небо между тучами.
Из этого примера возможно сделать вывод, что изучение пространственных форм ? это изучение качественных черт. Опять получается, что статическая геометрия это не только количественная, но и качественная наука, и по этому показателю родственна физике. Отличие же пребывает в том, что статическая геометрия оперирует одним природным свойством-качеством — протяженностью (остальные свойства являются для нее формальными особенностями), физика же охватывает всю совокупность природных качеств, не смотря на то, что применять в практике может лишь их мизерную часть.
Что же такое количество? Количество это отношение, создаваемое отечественным мышлением, это больше либо меньше, это появление эталона, что является мерилом отношения. Без этого отношения не может быть и счета.
Возможно проследить следующую последовательность появления цифр (счета). В сущности рис. 12. имеется неотёсанная аналогия мистического представления о происхождении Мира. (рис. 12):
Самостоятельно существует 1 и 1. А единственно по отношению к Б и напротив (рис. 12.). Но это отношение не формирует количества, т.к. А и Б имеется демонстрация того факта, что единственность, как познание, появляется из двойственности.
В случае, если А субъект, то Быть может заявить, что видит Б как отдельность (объект, тело), имеющую форму (границы). Отдельность Б есть полной, в случае, если А и Б не имеют ни одной «точки» соприкосновения. То, что находится между А и Б, не имеет формы и не может быть
 1. Исходное = ничто = все. 1. Исходное = ничто = все. |
2. Следующее = целое в потенции с внутренней границей 
|
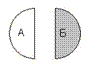 3. Разделение двух на отдельности и осознание единственности как первого отношения. 3. Разделение двух на отдельности и осознание единственности как первого отношения. |
Рис. 12.
зафиксировано как отдельность. Это побочный итог разделения. Назовем эту «аморфность» пространством и будем постоянно помнить, что это не пустота, не изначальное ничто, в котором «плавало» целое, а итог разделения. Исходя из этого с позиций статической геометрии количество, образуемый телом, не есть пространством, потому, что количество — конечная величина, легко определяемая через поверхность (внешнюю границу) тела, в случае, если исходить из внешнего измерителя. Пространство, образующееся при разделении тела, не может быть измерено, поскольку любой цикл (разделение пополам) будет машинально создавать и собственный эталон размера.
Итак, разделение потенциальных 2-х на отдельности разрешает А осознать (понять), что появление новых (вторых) объектов допустимо методом деления Б на отдельности. И А совершает эту операцию (фактически так же, как в случаях рис. 7 ¸9) для чего:
а) приближается к Б (перемещается в пространстве),
б) нарушает границу (разрушает) Б, сохраняя собственную целостность, но изменяя форму (становясь клином) и раздвигает Б, превращая его в Б1 и Б2. Разделение на Б1 и Б2 формирует между ними пространство, которое есть вторым по отношению к прошлому, поскольку оно создается уже тремя телами А, Б1, Б2. И это новое пространство разрешает А остаться между Б1 и Б2. Интуитивно мы поймём, ? это А уже не прежнее А, но оно может этого кроме того не «предполагать». Об этом знаем мы, поскольку машинально отодвинули себя на надёжное расстояние, чем перевоплотили А в тело подобное Б, т.е. из субъекта сделали объект А (колун). Отодвинув себя и сохранив А как телесность, мы зафиксировали очень занимательное явление, то есть:
Сознание имеет тенденцию не принимать участие в материальных процессах, а только следить за ними. Тем самым создавая эталон, как память о предшествующем состоянии. Применение памяти-эталона и имеется рождение количества. Лишь память на рис. 3 либо 4 знает, что конечный объект равен 1 по количеству отдельности имеется четверть и половина предшествующего по размеру (количеству). Но память – это прошлое. Тут вторая интуитивная предположение, что процесс разделения осуществляет контроль идея, которая материальна по отношению к сознанию и фактически бестелесна по отношению к нашему физическому миру [2]. Контрольная функция мысли в физическом ходе формирует его количественные характеристики и, в первую очередь, второе наименование отдельности. Появление А¢, Б1, Б2 все оставляет так же, как и прежде, другими словами 1 = отдельность А¢ «наблюдает» на себя, на Б1 и Б2 и констатирует, что существуют А¢ = 1; Б1 = 1; Б2 = 1 и по качеству отдельности (тело, вещь, объект) они все равны, другими словами 1 = 1 = 1 и А¢ = Б1 = Б2. В статике, визуально (через пространство) А¢ фиксирует, что все тела
различные по форме: А¢ ¹ Б1, А¢ ¹ Б2, Б1 ¹ Б2,
различные по количеству: — « — — « — — « — -,
различные по цвету: — « — — « — — « — и т.д.
Как следствие: Все тела в дискретном мире равны (однообразны) лишь по одному качеству — отдельности и это единственное уровень качества, которое разрешает оперировать безразмерностными цифрами числового последовательности как абстракциями. Исходя из этого постулирования типа «между любыми двумя цифрами натурального числового последовательности возможно поместить нескончаемое количество дробных, иррациональных и т.д. чисел» есть неправомерным, потому, что пространство между числами одного качества заполняется числами другого качества (уровень качества — «целое число», уровень качества -«дробное число») и позвано неосознанным рвением людской мышления к превращению дискретного в континуум.
Считается, что математика есть лишь абстрактной, количественной наукой, и все ее свойства, числа, индексы, фигуры являются формальными отображениями или некоторых количественных размеров, или схематического изображения настоящих тел. А потому никакие качественные характеристики не смогут быть свойственны формальным количественным размерам.
Но сами же числа не согласуются с этими предпосылками. Математические размеры — числа, не являются единообразными. Они делятся на отдельности: числа целые, дробные, иррациональные, мнимые, комплексные, гиперкомплексные и т.д. И, как будет продемонстрировано потом, это деление не просто так. Оно следствие диалектичности самих математических размеров, их необычной «формально-качественной» отдельности, и требует создания как следует разных правил с целью проведения математических операций с полным комплектом этих чисел. И потому, само существование целых чисел натурального последовательности как отдельностей не допускает возможности нахождения между ними дробных или других чисел, не относящихся к натуральному последовательности, как принадлежащих к второму качеству, к второй численной отдельности.
Еще раз выделим, что в математике каждое число из последовательности натуральных чисел есть целым по качеству отдельного, и промежутки между этими числами (целыми) не смогут быть заполнены никакими дробными размерами, потому, что дробные размеры имеется отдельное другого численного качества. В природе же дробное — в любой момент отображение не целого (отдельного), а численной величины качества. Отличие же в том, что целое (отдельное) не имеет размерности и по этому свойству сопоставимо лишь с другим целым (с другим отдельным), а природное уровень качества в любой момент величина размерная, в любой момент изменяемая и сопоставима с подобным и лишь с подобным изменяемым качеством.
Вклинивание иного качественного в ряды отдельного свидетельствует подмену понятий. Постулирование существования в одной форме различных качеств обусловливает нарушение качественной структуры математики. Оно вносит элемент несоответствия во «взаимоотношениях» между разными качествами числовых составляющих и обусловливает логическую неопределенность основаниям математики.
К тому же промежуток между арифметическими числами (либо знак промежутка, к примеру, пробел, «,», «;» и т.д.) отображает геометрическую составляющую математики — пространство (рис. 13). То самое действительно безлюдное математическое пространство, которое отделяет одно число от другого. (Пробел — формальная математическая «пустота». Он фиксирует отсутствие знаков между цифрами либо числами. Единственно допустимая в естественных науках пустота.)
 Пространство Простр. »_-_» и т.д. |
Рис. 13
Наличие в математике геометрической составляющей до сих пор математически не понято. И, потому, в математику, минуя познание математиков, незаметно и как бы противозаконно «влезает» геометрия, обусловливая существование отдельных чисел. Геометрия, которую уже нереально выделить из математики.
Рисунок 13 возможно представить и в второй форме (рис. 14):
И т.д.
Рис. 14
Изменение размещения тел, поменяло пространство — промежуток, образуемый отдельностями — телами. Попытки перевести дискретный мир в сплошной противозаконны, пока сохраняются качества отдельности. (А такая попытка, к примеру, наличествует кроме того в определении пространства Риманом [4]: «Пространство — постоянная совокупность однородных объектов либо явлений».) Из этого выражения: «разглядим множество целых чисел» либо «разглядим безлюдное множество» логически противоречивы, поскольку мысленный опыт, абстрагированный якобы от настоящего опыта, не опирается на данный самый опыт. К примеру, берем «мешок» (безлюдное множество). Засыпаем в него просо, песок и т.д. (числа, неизвестные отдельности различного качества) и, приравнивая, приобретаем винегрет качественности и бескачественности:
Количество = пространство = пустота.
Повторимся:
количество — отдельность, внешняя черта границ тела и он образуется телом. Тело везде «тащит» за собой собственный количество и никому его не даст. Без количества нет тела и нет количества без тела (трехмерное понятие);
пространство — размерностное уровень качества (промежуток между отдельностями, одномерное понятие), появляющееся при сотрудничестве тел. Следовательно, «мешок» появляется лишь при наличии тел. Нет тел, — нет и «мешка».
пустота — отсутствие качеств и отдельности. Как отсутствие всего она равнозначна такому целому, с которым человеческое мышление, будучи дискретным, не имеет ничего общего, и постигнуть ее, а, следовательно, и применять где бы то ни было нереально.
Как возможно сказать об абстрагировании до признания качества пустоты, если не осознается таковой несложный факт, что в пустоте нет и не может быть ничего по определению. В вакуум нереально «всунуть» никакое тело, и поля, числа либо пространства. Имеется тело, нет пустоты. Откуда возьмусь в том месте Я к тому же с мешком, из которого постоянно достану все, что лишь смогу вообразить?
Наличие логической путаницы в основаниях математики, в ее качествах и понятиях, игнорирование диалектичности Мира являются постоянными предпосылками происхождения неопределенности в ее структурах. Эти предпосылки расшатывают ее фундамент, предопределяя ненадежность тех логических построений, на которых зиждется все ажурное строение современной математики. Они обусловливают перманентный кризис в разных разделах математического мышления, что уже перерос в процесс, создающий угрозу всему формированию математики, в кризис, существование которого не отрицают и сами математики.