Тепловые процессы
И аппараты
ТЕПЛООБМЕН
Химические технологические процессы протекают в заданном направлении лишь при определенных температурах, каковые создаются методом подвода либо отвода тепловой энергии (теплоты). Процессы, скорость протекания которых зависит от скорости подвода либо отвода теплоты, именуются тепловыми. Движущей силой тепловых процессов есть разность температур между фазами. Аппараты, в которых осуществляются тепловые процессы, именуются теплообменниками, в них тепло переносится теплоносителями.
Расчет теплообменных аппаратов и процессов сводится в большинстве случаев к определению межфазной поверхности теплообмена. Эта поверхность находится из уравнения передачи тепла в интегральной форме. Коэффициент передачи тепла, как мы знаем, зависит от коэффициентов теплоотдачи фаз, и от термического сопротивления стены. Ниже будут рассмотрены методы их определения, тепловых поля потоков и нахождение температур. В том месте, где это быть может, искомые величины находятся из ответа уравнений законов сохранения, а в остальных случаях употребляются упрощенные математические модели либо способ физического моделирования.
Кондуктивный теплообмен в плоской стенке
Разглядим теплообмен в неподвижной плоской стенке
из однородного материала, теплофизические особенности которого постоянны
(сp, l, r = const) (рис. 1.1).
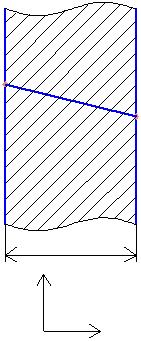
| y |
| T1 |
| T2 |
| x |
| d |
| ? |
Рис. 1.1. Распределение температуры в плоской стенке
Неспециализированное уравнение нестационарной теплопроводности Фурье имеет форму
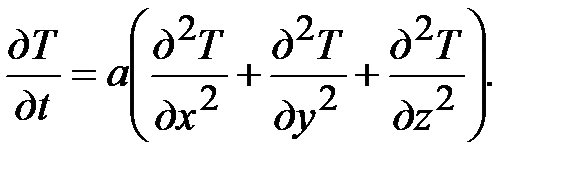 (1)
(1)
Процесс теплообмена стационарный, тогда 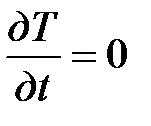 . Вычисляем,
. Вычисляем,
что длина и высота значительно больше толщины стены d, следовательно, теплообмен по этим направлениям отсутствует, тогда температура изменяется только на протяжении одной координаты х, из этого имеем
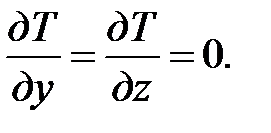
Потому, что 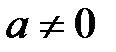 , имеем
, имеем
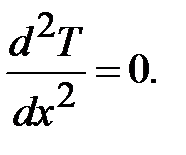 (2)
(2)
Очевидным ответом этого уравнения есть
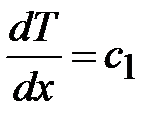 ,
,
откуда
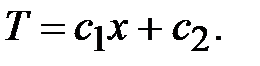 (3)
(3)
Граничные условия:
при 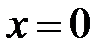
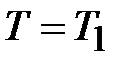 ;
;
при 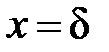
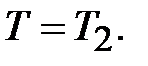
Находим 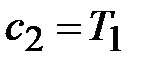 и
и 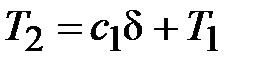 ,
, 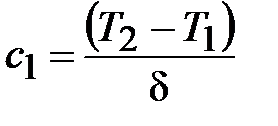 , тогда
, тогда
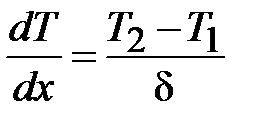 . (4)
. (4)
Распределение T по толщине d
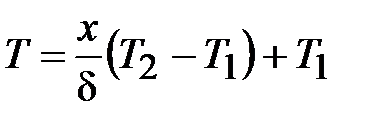 . (5)
. (5)
Из взятого уравнения (5) видно, что в плоской стенке распределение Т есть прямолинейным.
Поток тепла за счет теплопроводности определяется по закону Фурье
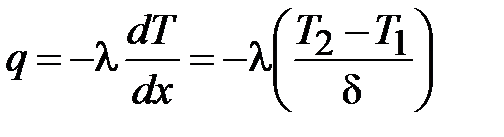 ; (6)
; (6)
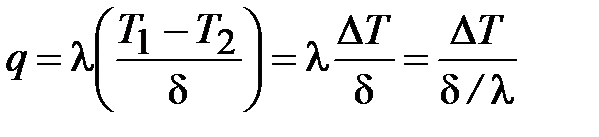 . (7)
. (7)
Тут 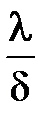 характеризует тепловую проводимость стены, а
характеризует тепловую проводимость стены, а 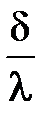 – термическое сопротивление стены.
– термическое сопротивление стены.
Для многослойной стены термическое сопротивление отдельных стенок нужно суммировать
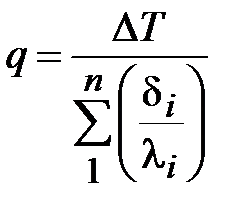 . (8)
. (8)
Определим количество теплоты, передаваемое за время t через площадь F
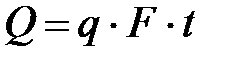 , (9)
, (9)
тогда расход тепла определяется как
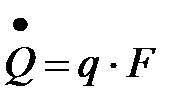 . (10)
. (10)
Тут F – поверхность пластины; t – время.
Но, приведенные расчетные формулы не всегда достаточны
для применения на практике. Как, к примеру, учесть термическое сопротивление стены при теплопередаче? Большей частью не редкость,
что температуры поверхностей Т1 и Т2 заблаговременно малоизвестны, но выяснены температуры Тср1 и Тср2 обеих сред, омывающих стенку,
и, помимо этого, соответствующие коэффициенты теплоотдачи a1 и a2. Тогда для случая передачи тепла расход тепла запишется
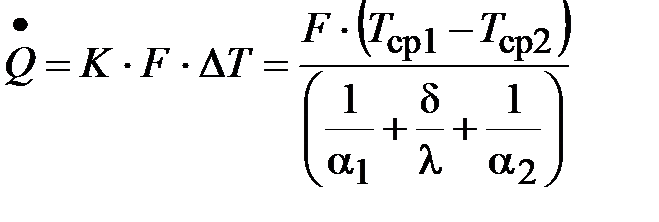 .
.
Конвективный теплообмен
При конвекции перенос теплоты происходит макрообъемными частицами потока теплоносителя. Конвекция постоянно сопровождается теплопроводностью. Как мы знаем, теплопроводность – явление молекулярное, конвекция – явление макроскопическое, при котором
в переносе теплоты участвуют целые слои теплоносителя с различными температурами. Конвекцией теплота переносится намного стремительнее, чем теплопроводностью. Конвекция у поверхности стены аппарата затухает.
1. Конвективный перенос теплоты описывается уравнением Фурье-Кирхгофа.
2. Закономерности течения среды описываются уравнениями Навье-Стокса (ламинарный режим) и Рейнольдса (турбулентный режим),
3. и уравнением неразрывности.
Изучение закономерностей конвективного теплообмена возможно провести в изотермической и неизотермической постановке.
В изотермической постановке сперва решаются уравнения Навье-неразрывности и Стокса, после этого полученные значения скоростей употребляются для ответа уравнения Фурье-Кирхгофа. Полученные таким методом значения коэффициентов теплоотдачи потом уточняются, корректируются.
В неизотермической постановке уравнения Навье-Стокса, неразрывности и Фурье-Кирхгофа решаются совместно, с учетом зависимости теплофизических особенностей среды от температуры.
Как показывают экспериментальные эти, зависимости ср (Т),  l(Т)
l(Т)
и r(Т) не сильный, а m(Т) – весьма сильная. Исходя из этого в большинстве случаев учитывается лишь зависимость m(Т). Она, эта зависимость, возможно представлена в виде зависимости Аррениуса либо, несложнее, в виде алгебраического уравнения. Так, появляются так именуемые сопряженные задачи.
Сейчас созданы способы ответа многих задач теплоотдачи в ламинарных потоках жидкости с учетом зависимости вязкости жидкости от температуры. Для турбулентных течений все сложнее. Но возможно применять приближенные численные ответы посредством компьютерных разработок.
На плоской пластине
Разглядим поток, владеющий неизменными теплофизическими чертями (r, m, l, cp = const), совершающий вынужденное перемещение на протяжении плоской полубесконечной узкой пластины и обменивающейся с ней теплом. Предположим, что неограниченный поток со температурой 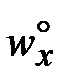
и скоростью Т° набегает на полубесконечную пластину, совпадающую
с плоскостью х – z и имеющую температуру Тст = const.
Выделим гидродинамический и тепловой пограничные слои
с толщиной dг и dт соответственно (область 99 % изменение скорости wx и температуры T). В ядре потока 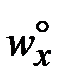 и Т° постоянны.
и Т° постоянны.
I. Ламинарные пограничные слои (рис. 1.3).
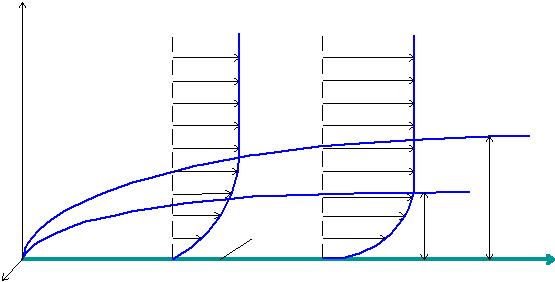
| y |
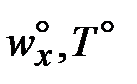
|
| wx |
| Tст |
| (T–Tст) |
| dг(x) |
| dт(x) |
| x |
| x |
| z |
Рис. 1.3. Гидродинамический и тепловой ламинарные пограничные слои
на плоской пластине
Проанализируем Навье Стокса и уравнения-неразрывности. Задача двумерная, потому, что wz, 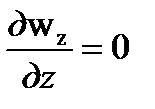 . По экспериментальным данным как мы знаем, что в гидродинамическом пограничном слое
. По экспериментальным данным как мы знаем, что в гидродинамическом пограничном слое 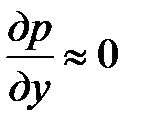 . В ядре потока
. В ядре потока 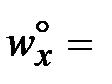 const, исходя из этого, в соответствии с уравнению Бернулли
const, исходя из этого, в соответствии с уравнению Бернулли 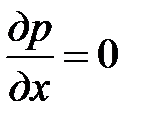 , в пограничном слое то же самое
, в пограничном слое то же самое 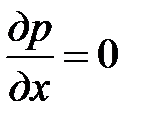 .
.
Как мы знаем x dг, исходя из этого 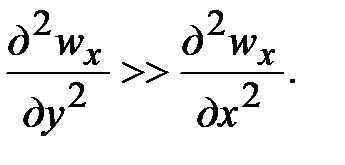
Следовательно, имеем
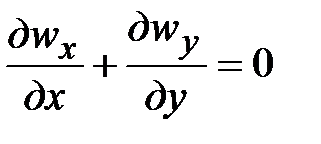 ; (22)
; (22)
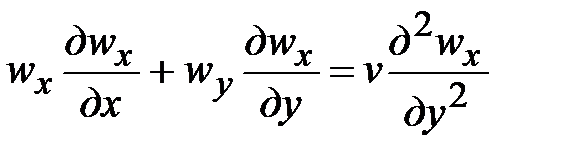 . (23)
. (23)
Записывать подобные уравнения для оси у не имеет смысла, поскольку wy возможно отыскана из уравнения неразрывности (22). Применяя подобные процедуры возможно упростить и уравнение Фурье-Кирхгофа
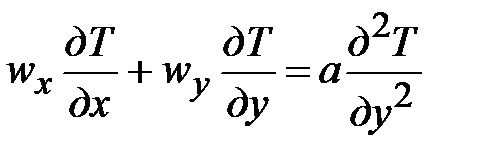 . (24)
. (24)
Совокупность дифференциальных уравнений (22)–(24) образовывает изотермическую математическую модель плоского стационарного теплового ламинарного пограничного слоя.
Сформулируем граничные условия
на границе с пластиной, т.е. при у = 0: при любом х скорость wx = 0 (условие прилипания). На границе и вне гидродинамического погранслоя,
т.е. при у ? dг(х), и при х = 0 для любого у: wx =  . Для поля температуры подобные рассуждения.
. Для поля температуры подобные рассуждения.
Итак, граничные условия:
wx (x, 0) = 0, x 0; wx (x, ?) =  ; wx (0, y) =
; wx (0, y) = 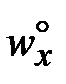 ; (25)
; (25)
T (x, 0) = Tст, x 0; T (x, ?) = 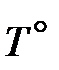 ; T (0, y) =
; T (0, y) = 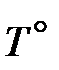 . (26)
. (26)
Правильное ответ данной задачи в виде нескончаемых последовательностей было получено Блазиусом. Имеются более простые приближенные ответы: способ интегральных соотношений (Юдаев) и теорема импульсов (Шлихтинг). А.И. Разиновым задача была решена способом сопряженного физического
и математического моделирования. Были взяты профили скоростей
wx (x, y), wy (x, y) и температур Т, и толщины пограничных слоев
dг(x) и dт (х)
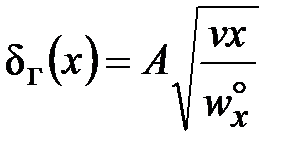 ; (27)
; (27)
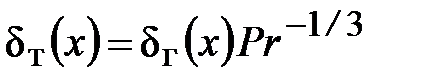 , Pr ? 1; (28)
, Pr ? 1; (28)
Pr = ?/a.
Коэффициент А в формуле (27) у Разинова – 5,83; Юдаева – 4,64; Блаузиуса – 4; Шлихтинга – 5,0. Примерный вид отысканных зависимостей приведен на рис. 1.3.
Как мы знаем, для газов Pr ? 1, капельных жидкостей Pr 1.
Полученные результаты разрешают выяснить коэффициенты импульсо-и теплоотдачи. Локальные значения ?(x) и Nuг,x
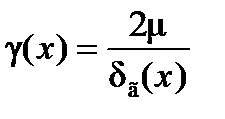
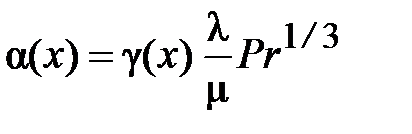
исходя из этого
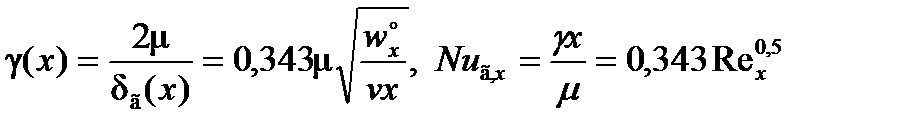 ,
,
где 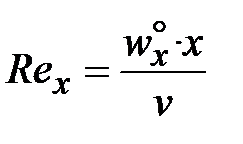 . (29)
. (29)
Усредненные значения 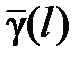 и
и 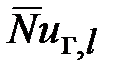 по участку длиной l
по участку длиной l
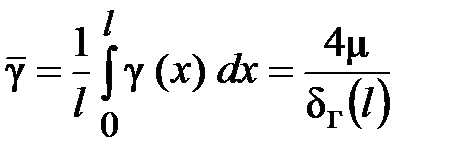 ,
, 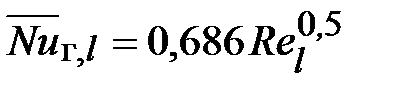 ,
, 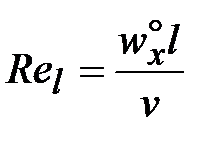 . (30)
. (30)
Результат для теплоотдачи
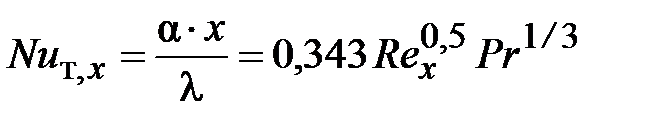 ; (31)
; (31)
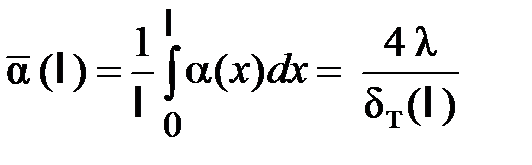 ,
, 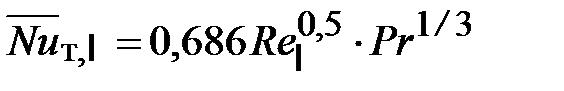 . (32)
. (32)
В этом случае аналогия тепло- и импульсоотдачи сохраняется (исходные уравнения однообразны, граничные условия подобны). Критерий, характеризующий гидродинамическую аналогию процесса теплоотдачи имеет форму
Pт-г,x = Nuт,x / Nuг,x = Pr1/3. (33)
В случае, если Pr = 1, то Pт-г,x = 1, следовательно полная аналогия процессов импульсо- и теплоотдачи.
Из взятых уравнений направляться
? ~ 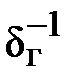 , m; a ~
, m; a ~ 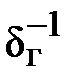 , l. (34)
, l. (34)
В большинстве случаев, подобная качественная зависимость выполняется
не только для плоского погранслоя, но и для более сложных случаев.
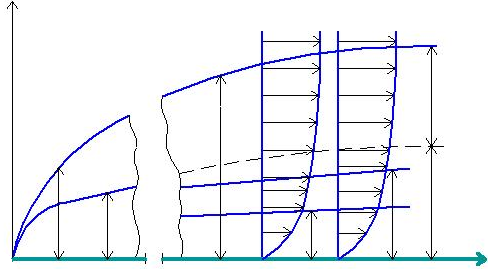
II. Турбулентные пограничные слои (рис. 1.4)
| у |
| х |
| dг dт |
| dт = dг |
| турбулентный слой |
| переходная область |
| z |
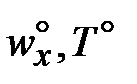
|
| внешняя область |
| d1т |
| пристенная область |
| d1г |
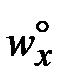
|
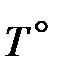 — Tст — Tст |
| ламинарный слой |
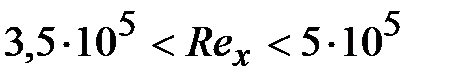
|
| Tст |
Рис. 1.4. Гидродинамический и тепловой турбулентные пограничные слои
на плоской пластине
Задача рассматривается в изотермической постановке, тепловые граничные условия первого рода Тст = const.
По мере удаления от кромки пластины (повышения координаты х) происходит рост dг(х). Наряду с этим неоднородность поля скорости wx распространяется в области все более удаленные от границы раздела фаз,
что есть предпосылкой происхождения турбулентности. Наконец, при Rex,кp начинается переход ламинарного режима в турбулентный. Переходная территория соответствует значениям х, вычисленным по Rex от 3,5 ? 105 ? 5 ? 105.
На расстояниях Rex 5 ? 105 целый пограничный слой турбулизируется,
за исключением вязкого либо ламинарного подслоя толщиной d1г. В ядре потока скорость не изменяется. В случае, если Pr 1 то в вязкого подслоя возможно выделить тепловой подслой толщиной d1т, в котором молекулярный перенос тепла преобладает над турбулентным.
Толщина же всего турбулентного теплового пограничного слоя в большинстве случаев определяется из условия ?т = ат, следовательно dг = dт.
Сперва разглядим турбулентный гидродинамический пограничный слой (рис. 1.4). Покинем в силе все приближения, сделанные для ламинарного слоя. Единственное отличие – наличие ?т (у), исходя из этого
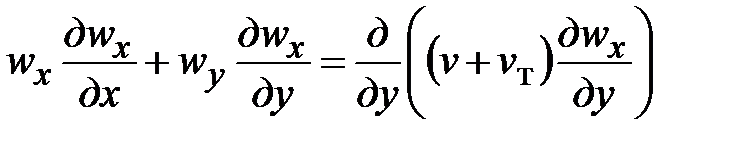 . (35)
. (35)
Сохраним и граничные условия. Ответом совокупности уравнений (35)
и (22) с граничными условиями (25), применяя полуэмпирическую турбулентности и модель Прандтля, возможно взять характеристики турбулентного пограничного слоя. В вязком подслое, где реализуется линейный закон распределения скорости, возможно пренебречь турбулентным переносом импульса, а вне его молекулярным. В пристенной области (за вычетом вязкого подслоя) в большинстве случаев принимается логарифмический профиль скорости, а во внешней области – степенной закон с показателем 1/7 (рис. 1.4).
Как и при ламинарного пограничного слоя допустимо применение осредненных по длине l коэффициентов импульсоотдачи
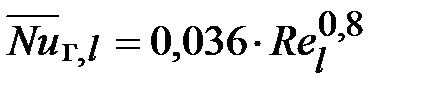 . (36)
. (36)
Разглядим тепловой турбулентный пограничный слой. Уравнение энергии имеет форму
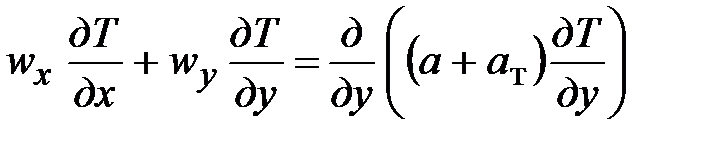 . (37)
. (37)
В случае, если Pr 1, то в вязкого подслоя возможно выделить тепловой подслой, где молекулярный перенос тепла
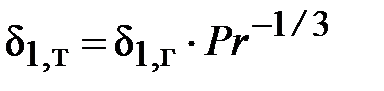 . (38)
. (38)
Для локального коэффициента теплоотдачи ответ математической модели имеет форму
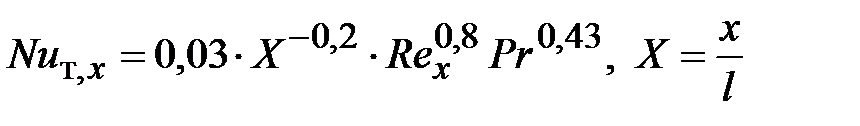 . (39)
. (39)
Среднее по длине пластины значение 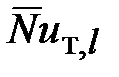 определяется так
определяется так
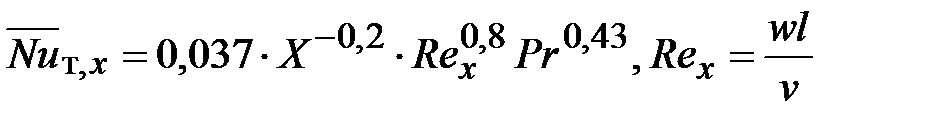 . (40)
. (40)
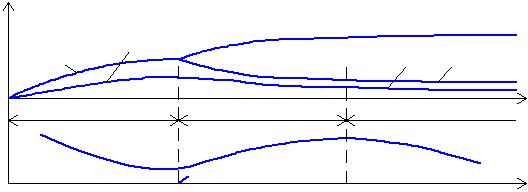
Ниже представлены образование турбулентного пограничного слоя (а) и распределение локального коэффициента теплоотдачи (б) при продольном обтекании плоской полубесконечной пластины (рис. 1.5).
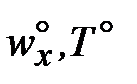
|
| y |
| x |
| dт |
| d1,т |
| d1,г |
| ?г = dт |
| lкр |
| x |
| ламинарный слой |
| переходная территория |
| турбулентный слой |
| a |
| dг |
Рис. 1.5. Пограничные слои dг и dт и локальный коэффициент теплоотдачи a
на плоской пластине
В ламинарном слое (х ? lкр) тепловой поток реализуется лишь за счет теплопроводности, для качественной оценки возможно применять соотношение a ~ 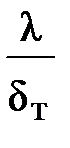 .
.
В переходной территории неспециализированная толщина пограничного слоя возрастает. Но значение a наряду с этим возрастает, в силу того, что толщина ламинарного подслоя значительно уменьшается, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией совместно
с перемещающейся массой жидкости, т.е. более интенсивно. В следствии суммарное термическое сопротивление теплоотдачи убывает. В зоне развитого турбулентного режима коэффициент теплоотдачи снова начинает убывать из-за возрастания неспециализированной толщины пограничного слоя a ~ 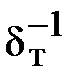 .
.
Итак, рассмотрены гидродинамический и тепловой пограничные слои на плоской пластине. Качественный темперамент взятых зависимостей честен и для пограничных слоев, образующихся при обтекании более сложных поверхностей.
Теплообмен в круглой трубе
Разглядим стационарный теплообмен между стенками горизонтальной прямой трубы круглого сечения и потоком, владеющим неизменными теплофизическими чертями и движущимся за счет вынужденной конвекции в нее. Примем тепловые граничные условия первого рода, т.е. Тст = const.
ОГЛАВЛЕНИЕ
| 1. ТЕПЛООБМЕН . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 1.1. Кондуктивный теплообмен в плоской стенке . . . . . . . . . . . . . . . . | |
| 1.2. Кондуктивный теплообмен в цилиндрической стенке . . . . . . . . . | |
| 1.3. Конвективный теплообмен . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 1.3.1. Гидродинамический и тепловой пограничные слои на плоской пластине . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 1.3.2. Теплообмен в круглой трубе . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 1.3.3. Теплообмен с телами сложной формы . . . . . . . . . . . . . . . . . . . | |
| 1.4. Теплообмен при трансформации теплофизических черт теплоносителя и его фазового состояния . . . . . . . . . . . . . . . . . . . . . . . . | |
| 1.4.1. Теплоотдача при конденсации пара . . . . . . . . . . . . . . . . . . . . . | |
| 1.4.2. Теплоотдача при кипении жидкостей . . . . . . . . . . . . . . . . . . . | |
| 1.5. Теплообмен при ярком контакте теплоносителей . . | |
| 1.6. Радиационно-конвективная теплоотдача. Тепловое излучение . . | |
| 1.7. интенсификация и Оптимизация теплообмена . . . . . . . . . . . . . . . | |
| Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 2. ПРОМЫШЛЕННЫЕ МЕТОДЫ Теплопередачи . . . . . | |
| 2.1. Подвод теплоты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 2.1.1. Нагревание паром и парами высокотемпературных теплоносителей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 2.1.2. Нагревание тёплыми жидкостями . . . . . . . . . . . . . . . . . . . . . . | |
| 2.2. Отвод теплоты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 2.3. конструкция и Классификация теплообменников . . . . . . . . . . . . . | |
| 2.3.1. Рекуперативные теплообменники . . . . . . . . . . . . . . . . . . . . . . | |
| 2.3.2. Регенеративные теплообменники . . . . . . . . . . . . . . . . . . . . . . . | |
| 2.3.3. Смесительные теплообменники . . . . . . . . . . . . . . . . . . . . . . . . | |
| 2.4. Методика расчета теплообменника . . . . . . . . . . . . . . . . . . . . . . . . . | |
| 2.4.1. Проектный расчет теплообменника . . . . . . . . . . . . . . . . . . . . . | |
| 2.4.2. Поверочный расчет теплообменника . . . . . . . . . . . . . . . . . . . . | |
Тепловые процессы
И аппараты
ТЕПЛООБМЕН
Химические технологические процессы протекают в заданном направлении лишь при определенных температурах, каковые создаются методом подвода либо отвода тепловой энергии (теплоты). Процессы, скорость протекания которых зависит от скорости подвода либо отвода теплоты, именуются тепловыми. Движущей силой тепловых процессов есть разность температур между фазами. Аппараты, в которых осуществляются тепловые процессы, именуются теплообменниками, в них тепло переносится теплоносителями.
Расчет теплообменных аппаратов и процессов сводится в большинстве случаев к определению межфазной поверхности теплообмена. Эта поверхность находится из уравнения передачи тепла в интегральной форме. Коэффициент передачи тепла, как мы знаем, зависит от коэффициентов теплоотдачи фаз, и от термического сопротивления стены. Ниже будут рассмотрены методы их определения, тепловых поля потоков и нахождение температур. В том месте, где это быть может, искомые величины находятся из ответа уравнений законов сохранения, а в остальных случаях употребляются упрощенные математические модели либо способ физического моделирования.
Кондуктивный теплообмен в плоской стенке
Разглядим теплообмен в неподвижной плоской стенке
из однородного материала, теплофизические особенности которого постоянны
(сp, l, r = const) (рис. 1.1).

| y |
| T1 |
| T2 |
| x |
| d |
| ? |
Рис. 1.1. Распределение температуры в плоской стенке
Неспециализированное уравнение нестационарной теплопроводности Фурье имеет форму
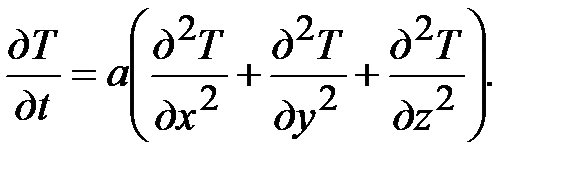 (1)
(1)
Процесс теплообмена стационарный, тогда 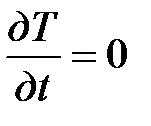 . Вычисляем,
. Вычисляем,
что длина и высота значительно больше толщины стены d, следовательно, теплообмен по этим направлениям отсутствует, тогда температура изменяется только на протяжении одной координаты х, из этого имеем
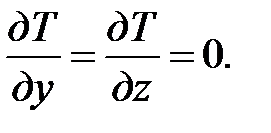
Потому, что 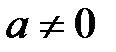 , имеем
, имеем
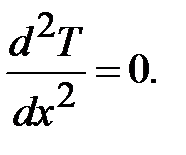 (2)
(2)
Очевидным ответом этого уравнения есть
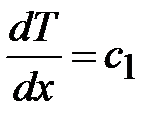 ,
,
откуда
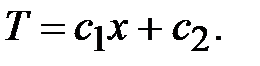 (3)
(3)
Граничные условия:
при 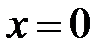
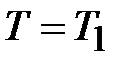 ;
;
при 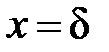
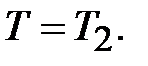
Находим 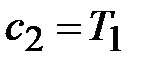 и
и 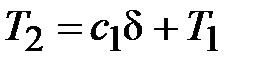 ,
, 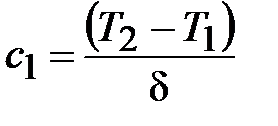 , тогда
, тогда
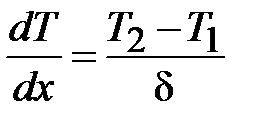 . (4)
. (4)
Распределение T по толщине d
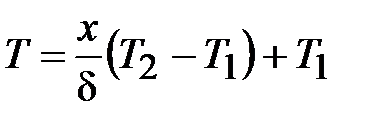 . (5)
. (5)
Из взятого уравнения (5) видно, что в плоской стенке распределение Т есть прямолинейным.
Поток тепла за счет теплопроводности определяется по закону Фурье
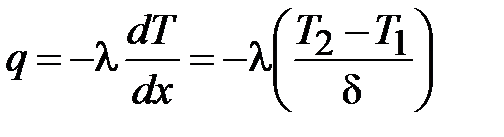 ; (6)
; (6)
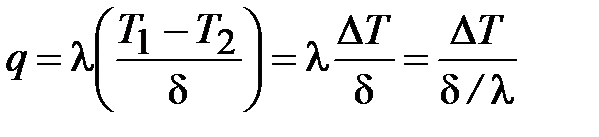 . (7)
. (7)
Тут 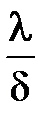 характеризует тепловую проводимость стены, а
характеризует тепловую проводимость стены, а 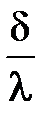 – термическое сопротивление стены.
– термическое сопротивление стены.
Для многослойной стены термическое сопротивление отдельных стенок нужно суммировать
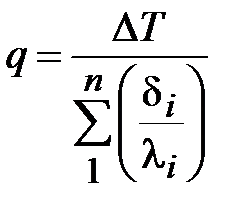 . (8)
. (8)
Определим количество теплоты, передаваемое за время t через площадь F
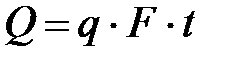 , (9)
, (9)
тогда расход тепла определяется как
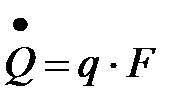 . (10)
. (10)
Тут F – поверхность пластины; t – время.
Но, приведенные расчетные формулы не всегда достаточны
для применения на практике. Как, к примеру, учесть термическое сопротивление стены при теплопередаче? Большей частью не редкость,
что температуры поверхностей Т1 и Т2 заблаговременно малоизвестны, но выяснены температуры Тср1 и Тср2 обеих сред, омывающих стенку,
и, помимо этого, соответствующие коэффициенты теплоотдачи a1 и a2. Тогда для случая передачи тепла расход тепла запишется
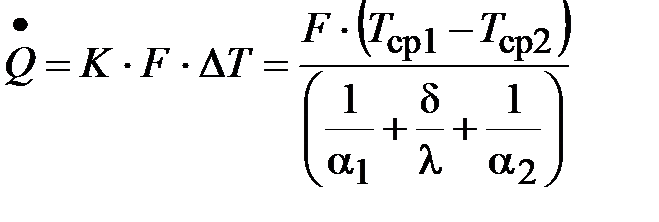 .
.