УДК 51-74
Составители: Л.И.Студеникина, Д.Н.Тютюнов
Критик
Кандидат физ-мат. наук, доцент кафедры
высшей математики В.И.Дмитриев
Элементы теории возможностей: индивидуальные задания и методические указания предназначены для организации независимой работы студентов профессий «Таможенное дело», «Интернациональные отношения» / Юго-Зап. гос. ун-т; сост.: Л.И.Студеникина, Курск, 2013. 40 с.: табл. 4. Библиогр.: с.40.
В данной работе находятся краткие теоретические положения, образцы исполнения типовых задач, 30 вариантов личных заданий.
Текст печатается в авторской редакции
Подписано в печать _______ . Формат 60х84 1/16.
Усл. печ. л. . Уч.-изд. л. . Тираж 50 экз. Заказ____. Безвозмездно.
Юго-Западный национальный университет305040 Курск, ул. 50 лет Октября, 94.
Введение
Эти методические указания предназначены для создания умений и навыков у студентов по разделу «Теория возможностей ».
Наличие таких индивидуальных заданий и указаний, имеющих опытную направленность в условиях сокращения аудиторных часов, представляется своевременным.
Теоретическое обеспечение по этому разделу математики достаточно полно отражено в учебных пособиях, предусмотренных рабочими программами. Однако, в данной работе даются краткие теоретические сведения и разобрано большое количество задач, что весьма комфортно при организации независимой работы.
Для подготовки студента к защите выполненных личных заданий представлен перечень литературы, отражающей полностью теоретический материал по данной теме.
Содержание
§ 1. Классификация событий……………………………………………….4
§ 2. Хорошая возможность. Комбинаторика……………….5
§ 3. умножения вероятностей и Правила сложения……………8
§ 4. Формула полной возможности. Формулы Байеса………..10
§ 5. Повторные опробования…………………………………….11
§ 6. Дискретная случайная величина………………………….14
§ 7. Постоянная случайная величина………………………17
§ 8. Теоретические вопросы…………………………………18
§ 9. Личные задания………………………………20
Рекомендуемая литература…………………………………47
§ 1. Классификация событий.
Опытом, либо опробованием, именуют всякое осуществление определенного комплекса условий либо действий, при которых происходит соответствующее явление. К примеру, бросание игрального кубика либо монеты, выстрел из оружия и т.д. Вероятный итог опыта именуют элементарнымсобытием,либо финалом. Множество ? всех вероятных взаимоисключающих финалов опыта именуется пространством элементарных событий либо пространством финалов. Событие по большому счету – это множество всех таких финалов, каковые вызывают его появление. О таких финалах говорят, что они помогают событию. События обозначаются большими буквами латинского алфавита А, В, С …. . К примеру, при однократном бросании монеты финал Г– выпадение герба, финал Р– выпадение решки, пространство?={Г,Р} ; в опыте с оружием финал А–попадание в мишень, В–промах. В опыте с кубиком финал А1 –выпало значение 1, А2 –значение 2, А3 –значение 3, А4 –значение 4, А5 –значение 5, А6 –значение 6, исходя из этого пространство элементарных событий ?={1,2,3,4,5,6}. Событию А –выпало нечетное число очков – помогают финалы А1, А3, А5.
Событие именуется точным в данном опыте, если оно непременно наступит в следствии данного опыта. К примеру, выпадение не меньше одного очка при бросании игральной кости.
Событие именуется неосуществимым,если оно заведомо не случится в следствии проведения опыта. Так выпадение числа 7 при броске игральной кости есть неосуществимым.
Два события именуются совместимыми в данном опыте, в случае, если появление одного из них не исключает появление другого в этом опыте, другими словами, в случае, если имеется хотя бы один финал, что помогает как одному событию, так и второму. Выпадение орла либо решки при подбрасывании двух монет – совместимые события.
Два события именуются несовместимымив данном опыте, если они не смогут случиться совместно при одном и том же опробовании. Несовместимыми являются промах и попадание при одном выстреле.
Два события именуются противоположными, в случае, если появление одного из них равносильно не появлению другого. К примеру, противоположными являются события выпадение орла либо решки при одном подбрасывании симметричной монеты.
События именуют равновозможными, в случае, если имеется основания вычислять, что ни одно из них не есть более вероятным, чем второе. К примеру, при подбрасывании игрального кубика события А1, А2, А3, А4, А5, А6 являются равновозможными.
Суммой А1+А2+…+Аn нескольких событий А1, А2,…, Аn именуется объединение множеств А1 E А2E… EАn. Так, событию А1+А2+…+Аn помогают те и лишь те финалы, любой из которых помогает хотя бы одному из событий А1, А2,…, Аn, другими словами событие А1+А2+…+Аn содержится в том, что происходит хотя бы одно из событий А1, А2,…, Аn.
Произведением нескольких событий А1, А2,…, Аn именуется пересечение множеств А1CА2C … C Аn. Произведение А1А2…Аn содержится в том, что происходит каждое из событий А1, А2,…, Аn.
Пара попарно несовместных событий образуютполную группу, в случае, если в следствии опробования никакие другие события, не считая перечисленных, не смогут случиться, другими словами А1+А2+…+Аn = ?.
Ответ.
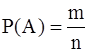
m=1000–80=920, число объявлений, заполненных правильно. Искомая возможность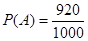 
=0,92.
Ответ.
Обозначим через А событие, пребывающее в том, что выбранный сотрудник — хороший эксперт, В1,В2 –догадки, пребывающие в том, что выбранный наугад сотрудник – выпускник первого, либо второго института соответственно. Наряду с этим по условию, Р(В1)=0,75; Р(В2)=0,25; (А)=0,95; 
(А)=0,9. В соответствии с формулами Байеса при n=2 имеем РА(В2)= 
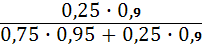=0,24. Обратите внимание на то, что знаменатель P(A)=0,75·0,95+0,25·0,9 вычисляется по формуле полной возможности.
Повторные опробования
На практике обычно приходится сталкиваться с обстановками, каковые возможно представить в виде многократно повторяющихся опробований при определенном комплексе условий. Наряду с этим ответственным не редкость определить итог не единичного опыта, а серии однообразных опробований.
В случае, если возможность наступления события А в каждом опробовании не изменяется в зависимости от финалов вторых, то такие опробования именуются свободными относительно события А. В случае, если свободные повторные опробования проводятся при одном и том же комплексе условий, то возможность наступления события А в каждом опробовании одинаковая. Обрисованная последовательность свободных опробований носит название схемы Бернулли.
Теорема.
Пускай производится n свободных опытов, в каждом из которых может показаться либо не показаться некое событие А, возможность появления события А в каждом опыте равна р, а возможность не появления q=1-p. Тогда возможность того, что событие А покажется в n свободных опробованиях ровно k раз, равна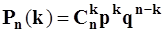 
.
Эта формула именуется формулой Бернулли.
Пример.При заполнении таможенной декларации нужно ответить на 6 вопросов. Возможность верного ответа на любой вопрос 0,9. Отыскать возможность верного ответа на 5 из поставленных вопросов.
Ответ.Возможность события А (верный ответ при заполнении декларации) р=0,9, тогда q= 1-0,9=0,1. Искомая возможность равна =6·0,591·0,1=0,354
Наивероятнейшим числом появления события А в n свободных опробованиях именуется такое число k0, для которого возможность Pn(k0) превышает либо, по крайней мере, не меньше возможности каждого из остальных вероятных чисел k появления события A, другими словами Pn(с)? Pn(k). Для определения наивероятнейшего числа не обязательно вычислять возможности вероятных чисел появлений события, достаточно знать число опробований n и возможность появления события A в отдельном опробовании. В случае, если произведено n свободных опробований и возможность появления события А в каждом из них равна р¹0, то наивероятнейшее число k0 заключено в пределах .
Пример.Возможность получения успешного результата при досмотре груза на пограничном таможенном пункте
(обнаружение в грузе запрещенных веществ) равна 0,75. Отыскать наивероятнейшее число хороших результатов, в случае, если общее число досмотров за одну смену равняется 10.
Ответ. В этом примере n=10, p=0,75, q=0,25.Неравенство имеет форму , . Лишь одно целое число есть ответом этого двойного неравенства – число k0=8.
В случае, если число опробований n громадно, то вычислять возможности по формуле Бернулли становится весьма проблематично. В этих обстоятельствах применяют формулы для приближенного значения возможностей Pn(k).
Локальная теорема Лапласа.
В случае, если возможность р появления события А в каждом опробовании постоянна и хороша от единицы и нуля, то возможность того, что событие А покажется в n опробованиях ровно k раз, выражается приближенной формулой
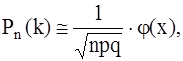
где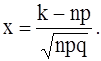 
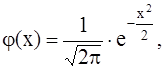— функция четная, ее значения протабулированы и сведены в таблицу, в зависимости от значений х. В случае, если х ³ 4, то j(х) = 0.
Пример. Возможность поражения мишени биатлонистом при одном выстреле р=0,85. Отыскать возможность того, что при 100 выстрелах спортсмен поразит мишень 90 раз.
Ответ.
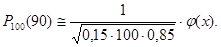
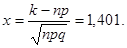
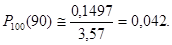
Ответ.
а) p=0,1; q=0,9; k1=2; k2=12; n=100.
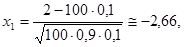
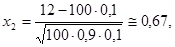
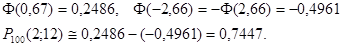
Погрешность указанной формулы не превосходит 
,так что она есть достаточно правильной при громадных значениях npq.
Задание 1
Комбинаторика.
1. какое количество трехзначных чисел возможно составить из цифр 2,5,6,7, применяя в записи числа каждую из них не более одного раза.
2. У Петра пятеро друзей: Саша, Дима, Олег, Федя, Сергей. Петру подарили три пригласительных билета на концерт. Укажите все вероятные варианты выбора двух друзей для похода на концерт. какое количество всего таких вариантов?
3. Пребывав в условиях задачи №2, Петр решил все пригласительные билеты дать приятелям. Какие конкретно наряду с этим вероятны варианты? какое количество таких вариантов?
4. Из цифр 1,2,3 составьте все вероятные двузначные числа при условии, что: а) цифры не повторяются; б) цифры смогут повторяться.
5. На интернациональную конференцию прибыло 25 представителей разных государств. Но, в виду регламента выступить с докладом смогут только 15 участников конференции. какое количество методами возможно выбрать этих 15 выступающих.
6. В отделе МИДа 12 сотрудников обладают китайским языком и 7 — арабским. С целью проведения конференции требуется выделить 4 сотрудников, обладающих китайским, и 2 – арабским. какое количество методами это возможно сделать?
7. Почтальон обязан разнести 5 писем в 5 разных организаций. какое количество маршрутов он может выбрать?
8. какое количество методами смогут распределиться призовые места среди 9 участников спортивных соревнований?
9. какое количество методами возможно сшить триколор с горизонтальными полосами, в случае, если имеется материал из шести разных цветов?
10. какое количество методами 8 человек смогут подняться в очередь в ЖД кассу за билетами?
11. какое количество шестизначных чисел (без повторения цифр) возможно составить из цифр 1,2,3,4,5,6?
12. какое количество существует шестизначных телефонных номеров, в которых все цифры разные и первая цифра хороша от нуля?
13. В шахматном турнире участвуют 9 человек. Любой из них сыграл с каждым по одной партии. какое количество всего партий было сыграно?
14. На станции 8 запасных дорог. какое количество методами возможно расставить на них 5 поездов?
15. какое количество существует семизначных телефонных номеров, в которых все цифры разны и первая цифра хороша от нуля?
16. какое количество методами 5 студентов, сдающих экзамен, смогут занять места в аудитории, в которой стоят 16 одноместных столов?
17. В группе 6 студентов удачно занимаются математикой. какое количество методами возможно выбрать двух студентов для принятие участия в олимпиаде по математике?
18. В группе 12 парней и 7 девушек. Для уборки территории требуется выделить 4 девушки и 2 парня. какое количество методами это возможно сделать?
19. какое количество методами возможно выбрать три лица на три разные должности из 11 кандидатов?
20. какое количество разными методами смогут разместиться за круглым столом 5 человек?
21. какое количество методами возможно выбрать три лица на три однообразные должности из 10 кандидатов?
22. Из отдела, в котором трудятся заведующий отделом и 7 сотрудников, в командировку должны отправиться 3 человека. какое количество методами это возможно сделать, в случае, если: а) заведующий отделением обязан ехать в командировку; б) заведующий отделением не должен ехать в командировку.
23. Женщина не забывает, что телефон подруги оканчивается цифрами 9,4,3, но забыла, в каком порядке эти цифры следуют. Указать наибольшее число вариантов, каковые ей нужно будет перебрать, дабы дозвониться подруге.
24. какое количество методами смогут быть расставлены 8 участников финального забега на восьми беговых дорожках?
25. На соревнования по легкой атлетике приехала команда из 12 спортсменок. какое количество методами тренер может выяснить, кто из них побежит в эстафете 4 на 100 м на первом, втором, четвёртом этапах и третьем?
26. В книжном магазине продается 6 разных комплектов, посвященных олимпийской тематике. какое количество методами возможно выбрать три из них?
27. какое количество существует выражений, тождественно равных произведению abcde, каковые получаются из него перестановкой множителей.
28. В читальном зале студенту внесли предложение на выбор из журналов поступлений 10 и новых 5 книг. какое количество методами возможно выбрать 3 журнала и 2 книги?
29. какое количество методами возможно распределить 7 различных книг между семью студентами?
30. В комнате имеется 6 стульев. какое количество методами возможно разместить на них 6 приглашенных дипломатов?
Задание 2
Хорошая возможность
1. Из 18 собранных телевизоров 4 были с недостатками. Какова возможность того, что 2 наугад выбранные телевизора будут без недостатков?
2. Какова возможность того, что при бросании игрального кубика выпадет более 3-х очков?
3. Студент записал в тетрадь произвольное двузначное число. Какова возможность того, что сума цифр этого числа выяснилось равной 6?
4. Для открытия сейфа нужно собрать в определенной последовательности пять цифр (без их повторения): 1, 2, 3, 4, 5. Какова возможность того, что собрав цифры в произвольном порядке, вы откроете сейф?
5. В пачке находятся однообразные по размеру тетради: 8 тетрадей в линейку и 6 в клетку. Из пачки наугад берут 3 тетради. Какова возможность того, что это тетради в клетку?
6. В коробке 6 красных и 4 зеленых карандаша. Из коробки наугад вынимают 5 карандашей. Какова возможность того, что среди них 3 красных и 2 зеленых?
7. В коробке 10 подробностей, одна из которых нестандартная. Наугад берут 2 подробности. Какова возможность того, что обе подробности окажутся стандартными?
8. Кинуты 2 игральные кости. Отыскать возможность того, что сумма выпавших очков не превосходит 7?
9. Из букв А, Е, Ж, К,М,Н,О, Т составляется наугад слово, складывающееся из 6 букв. Какова возможность того, что окажется слово «ТАМОЖЕННИК»?
10. В партии из 10 подробностей имеется 3 бракованные. Наугад отобраны 3 подробности. Тогда возможность того, что все отобранные подробности будут бракованными, равна..
11. В коробке 20 подробностей, 4 из них – нестандартные. Какова возможность того, что среди 6 наугад забранных подробностей нестандартных не окажется?
12. В коробке 20 подробностей, 4 из них – нестандартные. Какова возможность того, что среди 6 наугад забранных подробностей окажется 5 стандартных и 1 нестандартная?
13. Игральная кость кидается 1 раз, тогда возможность того, что число очков, выпавших на верхней грани, будет меньше трех, равна…
14. Для новогодней лотереи отпечатали 1000 билетов, из которых 80 выигрышных. Какова возможность того, что приобретённый билет окажется выигрышным?
15. 4 билета в театр распределили по жребию между 15 девочками и 12 мальчиками, какова возможность того, что билеты достались 2 девочкам и 2 мальчикам?
16. В книге 250 страниц. Чему равна возможность того, что наугад открытая страница будет иметь порядковый номер, кратный 5?
17. Подбрасываются 2 игральных кубика, подсчитывается сумма очков на верхних гранях. Что возможнее: взять в сумме 7 либо 8?
18. Наугад выбрано натуральное число, не превосходящее 30. Какова возможность того, что это число кратно 3?
19. Наугад выбрано натуральное число, не превосходящее 10. Какова возможность того, что это число есть несложным?
20. Из букв слова «дифференциал» наугад выбирается 1 буква. Какова возможность того, что эта буква будет: а) гласной; б) согласной; в) ч?
21. На пяти однообразных карточках написаны буквы: У, Р, К, Ч, А. Карточки перемешиваются и наугад складываются в ряд. Какова возможность того, что окажется слово «РУЧКА»?
22. Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Какова возможность того, что среди обладателей билетов окажется 2 девушки?
23. В партии из 15 подробностей имеется 9 стандартных. Наудачу отобраны 6 подробностей. Отыщите возможность того, что среди отобранных подробностей 4 стандартных.
24. В группе 11 девушек и 11 юношей. Для дежурства случайным образом отобраны 3 студента. Отыщите возможность того, что все дежурные окажутся парнями?
25. В коробке 9 белых и 2 тёмных шаров. Отыщите возможность того, что из двух вынутых наудачу шаров один белый, а второй тёмный. Вынутый шар в урну не возвращается.
26. В партии из 17 подробностей имеется 9 стандартных. Наудачу отобраны 9 подробностей. Отыщите возможность того, что среди отобранных подробностей ровно 4 стандартных.
27. В коробке 4 голубых и 5 красных шаров. Из коробки наугад вынимают 2 шара. Отыщите возможность того, что эти шары различного цвета.
28. Из 10 билетов выигрышными являются 2. Чему равна возможность того, что среди забранных наудачу 5 билетов один выигрышный?
29. В коробке 10 шаров, из которых 2 белых, 3 красных и 5 голубых. Наудачу извлечены 3 шара. Отыщите возможность того, что все 3 шара различного цвета.
30. Студент выучил к экзамену 20 вопросов из 30. Билет складывается из трех вопросов. Какова возможность того, что студент знает все 3 вопроса?
Задание 3
Задание 4
Задание 5
Задание 6
ЗАКЛЮЧЕНИЕ
Одной из наиболее значимых функций математики как фундаментальной науки есть создание теоретической научной базы знаний для успешного овладения дисциплинами опытного цикла и формирование у студентов мышления, при котором осуществляется целостный подход к изучаемому предмету как к совокупности, складывающейся из множества взаимосвязанных элементов.
Математика, традиционно являясь необходимой составляющей инженерного образования, выступает как универсальный, общенаучный способ познания, является инструментом построения теории вторых наук. Вузовская математическая подготовка студентов обусловлена возросшими потребностями современной высшей школы в совершенствовании подготовки конкурентоспособного эксперта, могущего на научной базе организовывать собственный труд, разбирать собственные возможности, покупать новые знания.
В ходе изучения математики нужно воспитать у студентов высокую математическую культуру, достаточную для применения математического аппарата в будущей профессиональной деятельности.
При написании данного методического пособия авторы попытались продемонстрировать возможности интегрального исчисления для ответа целого класса задач. Пособие содержит много детально разобранных заданий, что очень актуально при независимой работе. Работа с предлагаемыми приложениями будет нужна для создания умений и навыков фактически по всем темам интегрального исчисления, изучаемым в институте.
Большой количество приложений разрешает закрепить изученный материал в достаточной степени для предстоящего применения на практике.
Рекомендуемая литература.
В.Е. Гмурман Управление к ответу задач по математической статистике и теории вероятностей: Учеб. Пособие для студентов институтов–8-е изд., стер.–М.: Высш. шк., 2003 г.,–405 с.
Е.С. Кочетков, С.О. Смерчинская Теория возможностей в упражнениях и задачах. М.: Форум – Инфра – М, 2005.
М.С. Красс, Б.П. Чупрынов, Математика для экономистов.–СПБ.: Питер,2006 г.,464 с.
А.А. Гусак, Е.А. Бричикова, Теория возможностей, справочное пособие к ответу задач.–Изд-е 4-е,стереотип.–Минск: ТетраСистемс,2003 г., 288 с.
Предисловие
На данный момент случилось значительное сокращение аудиторного времени на изучение математических дисциплин. Исходя из этого, наличие учебного пособия, компактно содержащего краткие большое количество и теоретические сведения детально разобранных задач соответствующей тематики и допускающего возможность его универсального применения, выясняется очень нужным.
Настоящее пособие абсолютно соответствует учебным программам курса математики для инженерных профессий и предназначается как для учителей (с обучающими и осуществляющими контроль качествами), так и для студентов (изучение, овладение и освоение материалом раздела – модуля курса). Пособие возможно использовано на практических занятиях по математике, при независимой работе над разделом курса, при исполнении личных заданий студентами разных форм обучения.
Преимущество данной работы перед подобными содержится, в большой мере, в высокой доступности, достигаемой за счет тщательной детализации применяемых способов.
Очевидно, предлагаемое пособие не имеет возможности претендовать на замену каких – или легендарных учебных изданий по данной тематике. Однако, авторы предполагают, что и преподавателям и студентам будет комфортно применять его в собственной работе.
УДК 51-74
Составители: Л.И.Студеникина, Д.Н.Тютюнов
Критик
Кандидат физ-мат. наук, доцент кафедры
высшей математики В.И.Дмитриев
Элементы теории возможностей: индивидуальные задания и методические указания предназначены для организации независимой работы студентов профессий «Таможенное дело», «Интернациональные отношения» / Юго-Зап. гос. ун-т; сост.: Л.И.Студеникина, Курск, 2013. 40 с.: табл. 4. Библиогр.: с.40.
В данной работе находятся краткие теоретические положения, образцы исполнения типовых задач, 30 вариантов личных заданий.
Текст печатается в авторской редакции
Подписано в печать _______ . Формат 60х84 1/16.
Усл. печ. л. . Уч.-изд. л. . Тираж 50 экз. Заказ____. Безвозмездно.
Юго-Западный национальный университет305040 Курск, ул. 50 лет Октября, 94.
Введение
Эти методические указания предназначены для создания умений и навыков у студентов по разделу «Теория возможностей ».
Наличие таких индивидуальных заданий и указаний, имеющих опытную направленность в условиях сокращения аудиторных часов, представляется своевременным.
Теоретическое обеспечение по этому разделу математики достаточно полно отражено в учебных пособиях, предусмотренных рабочими программами. Однако, в данной работе даются краткие теоретические сведения и разобрано большое количество задач, что весьма комфортно при организации независимой работы.
Для подготовки студента к защите выполненных личных заданий представлен перечень литературы, отражающей полностью теоретический материал по данной теме.
Содержание
§ 1. Классификация событий……………………………………………….4
§ 2. Хорошая возможность. Комбинаторика……………….5
§ 3. умножения вероятностей и Правила сложения……………8
§ 4. Формула полной возможности. Формулы Байеса………..10
§ 5. Повторные опробования…………………………………….11
§ 6. Дискретная случайная величина………………………….14
§ 7. Постоянная случайная величина………………………17
§ 8. Теоретические вопросы…………………………………18
§ 9. Личные задания………………………………20
Рекомендуемая литература…………………………………47
§ 1. Классификация событий.
Опытом, либо опробованием, именуют всякое осуществление определенного комплекса условий либо действий, при которых происходит соответствующее явление. К примеру, бросание игрального кубика либо монеты, выстрел из оружия и т.д. Вероятный итог опыта именуют элементарнымсобытием,либо финалом. Множество ? всех вероятных взаимоисключающих финалов опыта именуется пространством элементарных событий либо пространством финалов. Событие по большому счету – это множество всех таких финалов, каковые вызывают его появление. О таких финалах говорят, что они помогают событию. События обозначаются большими буквами латинского алфавита А, В, С …. . К примеру, при однократном бросании монеты финал Г– выпадение герба, финал Р– выпадение решки, пространство?={Г,Р} ; в опыте с оружием финал А–попадание в мишень, В–промах. В опыте с кубиком финал А1 –выпало значение 1, А2 –значение 2, А3 –значение 3, А4 –значение 4, А5 –значение 5, А6 –значение 6, исходя из этого пространство элементарных событий ?={1,2,3,4,5,6}. Событию А –выпало нечетное число очков – помогают финалы А1, А3, А5.
Событие именуется точным в данном опыте, если оно непременно наступит в следствии данного опыта. К примеру, выпадение не меньше одного очка при бросании игральной кости.
Событие именуется неосуществимым,если оно заведомо не случится в следствии проведения опыта. Так выпадение числа 7 при броске игральной кости есть неосуществимым.
Два события именуются совместимыми в данном опыте, в случае, если появление одного из них не исключает появление другого в этом опыте, другими словами, в случае, если имеется хотя бы один финал, что помогает как одному событию, так и второму. Выпадение орла либо решки при подбрасывании двух монет – совместимые события.
Два события именуются несовместимымив данном опыте, если они не смогут случиться совместно при одном и том же опробовании. Несовместимыми являются промах и попадание при одном выстреле.
Два события именуются противоположными, в случае, если появление одного из них равносильно не появлению другого. К примеру, противоположными являются события выпадение орла либо решки при одном подбрасывании симметричной монеты.
События именуют равновозможными, в случае, если имеется основания вычислять, что ни одно из них не есть более вероятным, чем второе. К примеру, при подбрасывании игрального кубика события А1, А2, А3, А4, А5, А6 являются равновозможными.
Суммой А1+А2+…+Аn нескольких событий А1, А2,…, Аn именуется объединение множеств А1 E А2E… EАn. Так, событию А1+А2+…+Аn помогают те и лишь те финалы, любой из которых помогает хотя бы одному из событий А1, А2,…, Аn, другими словами событие А1+А2+…+Аn содержится в том, что происходит хотя бы одно из событий А1, А2,…, Аn.
Произведением нескольких событий А1, А2,…, Аn именуется пересечение множеств А1CА2C … C Аn. Произведение А1А2…Аn содержится в том, что происходит каждое из событий А1, А2,…, Аn.
Пара попарно несовместных событий образуютполную группу, в случае, если в следствии опробования никакие другие события, не считая перечисленных, не смогут случиться, другими словами А1+А2+…+Аn = ?.
Хорошая возможность. Комбинаторика.
Комбинаторика изучает методы подсчета числа элементов в конечных множествах. Формулы комбинаторики применяют при ярком вычислении возможностей. Базисными конфигурациями комбинаторики являются: перестановки, размещения, сочетания.
Перестановками именуют комбинации, складывающиеся из одних и тех же n разных элементов и отличающиеся лишь порядком их размещения. Число всех вероятных перестановок конечного множества из n элементов равняется n!= обозначается Pn, так
Пример. какое количество существует разных способов составить очередь из 5 человек?
Ответ. Очередь – это перестановка из 5 элементов (человек), исходя из этого количество разных очередей равняется методам.
Размещениямииз n элементов по mназывают комплекты, которые содержат m разных элементов из данных n элементов, и отличающиеся или составом элементов, или их порядком. Число всех вероятных размещений из n элементов по m определяется формулой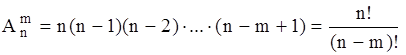 
Пример. какое количество разными методами возможно выбрать три лица на три разные должности из десяти кандидатов?
Ответ. Задача сводится к нахождению числа размещений из 10 элементов по 3:
Сочетаниями из n элементов по mназывают комплекты, которые содержат m элементов из данных n элементов и отличающиеся составом элементов (порядок размещения элементов, другими словами сочетание – это легко подмножество множества заданных элементов). Число всех сочетаний из n по m выражается формулой
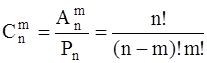
Пример. На таможенном посту смена складывается из 6 человек. какое количество методами возможно отобрать из 10 сотрудников одну смену?
Ответ.Смена – это сочетание из 10 человек по 6. Исходя из этого искомое число способов равняется
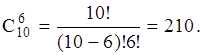
В комбинаторике рассматриваются кроме этого конфигурации, в которых допускаются неоднократные повторения одних и тех же элементов. К примеру, число 1231241 является перестановкой , в которой элемент 1 повторяется 3 раза, элемент 2 –2 раза, 3 и 4 по одному разу. Это перестановки с повторениями (порядок размещения элементов ответствен), вычисляются по формул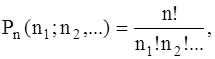е 
где
В случае, если кое-какие элементы повторяются, то в этом случае комбинации с повторениями вычисляют по вторым формулам. К примеру, в случае, если среди n элементов имеется элементов одного вида, элементов другого вида и т.д., то число перестановок с повторениями.
В случае, если в размещениях из n элементов по m не запрещаеться неоднократное применение любого элемента, то получаются комплекты, каковые именуются размещениями с повторениями из n элементов по m. Число таких размещений равняется nm. К примеру, количество четырехзначных чисел, все цифры которых нечетны, равняется 54=625, так как любое такое число является размещением из 5 цифр 1,3,5,7,9 по 4 (3531, 1977 и т.п.).
Возможностью события А именуют отношение числа помогающих этому событию финалов к неспециализированному числу всех финалов. Наряду с этим предполагается, что все финалы равновозможны.
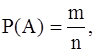
где m – число финалов, помогающих А;
n – число всех вероятных финалов опробования.
Из определения возможности вытекают ее свойства.
Свойство 1. Возможность точного события равна единице.
Свойство 2. Возможность неосуществимого события равняется нулю.
Свойство 3. Возможность случайного события имеется положительное число, заключенное между единицей и нулём.
Пример. Из 1000 таможенных объявлений, лежащих в стопке, 80 заполнены неверно. Какова возможность, что наудачу забранная декларация, будет заполнена правильно?
Ответ.
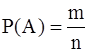
m=1000–80=920, число объявлений, заполненных правильно. Искомая возможность 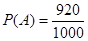=0,92.