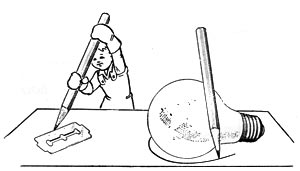
Не каждый предмет возможно спроектировать при помощи карандаша.
Самый несложный метод — это положить его на бумагу и обвести узким карандашом. Но не каждый предмет возможно спроектировать таким методом. Одни предметы не поместятся на странице, другие через чур мелки, а третьи (к примеру, электрическую лампочку) нереально обвести из-за сложности их формы.
Помимо этого, нас интересует не только внешний вид предмета, но и его внутреннее устройство, которое таким методом на бумагу не спроектируешь. Вот тут-то нам и пригодятся правила и приёмы начертательной геометрии.
Обозначим буквой А какую-нибудь точку на проектируемом предмете. Тогда мы сможем заявить, что точка А — это оригинал, точка а — проекция оригинала, А а — проектирующий луч, плоскость Р — плоскость проекции.
То же самое мы можем сообщить обо всех точках предмета. Следовательно, для получения проекции предмета, нужно спроектировать все его точки.
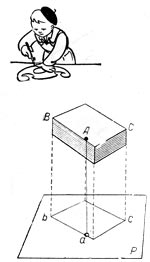
Дабы спроектировать предмет на плоскость, нужно спроектировать все его точки.
Но правила и законы начертательной геометрии разрешают существенно упростить Эту работу. Вправду, дабы выстроить проекции прямой, достаточно спроектировать лишь две каждые принадлежащие ей точки и совершить через них прямую линию. Проекции квадрата, прямоугольника либо треугольника возможно выстроить по проекциям их вершин.
Многие машин — детали и предметы зданий, мебель, посуда — содержат в себе элементы поверхностей и кривых линий. Для получения их проекций приходится кроме этого проектировать последовательность принадлежащих им точек и соединять эти точки между собой при помощи шаблонов—лекал. Такие линии стали называться лекальных.
Среди бесчисленного многообразия кривых имеется так именуемые закономерные кривые, все точки которых владеют некоторым неспециализированным свойством. Это свойство разрешает применить определенные правила для их начертания. К примеру, шар во всех проекциях имеет форму окружности. Ее не нужно строить по отдельным точкам, ее возможно совершить посредством циркуля. Проекция дна наклоненного либо срезанного плоскостью кругового цилиндра представляет собой другую закономерную кривую — эллипс. Видятся и более сложные закономерные кривые, и для каждой из них имеется собственные методы построения.
Но умения верно выстроить проекцию того либо иного предмета еще слишком мало для верного составления чертежей.
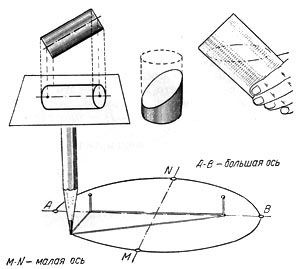
Проекция дна наклоненного либо срезанного цилиндра является эллипсом . Выстроить эллипс возможно методом, продемонстрированным на рисунке.
Одна из ответственных изюминок прямоугольных проекций содержится в том, что многие предметы разной формы проектируются одинаково на одну, а время от времени и на две плоскости проекции. К примеру, горизонтальную проекцию в виде круга имеют шар, цилиндр, конус. Дабы их различить, непременно нужна вторая проекция. Но не всегда помогает и она. Приходится чертить третью проекцию.
В тех случаях, в то время, когда по прямоугольным проекциям тяжело представить себе неспециализированный вид изображенного предмета, прибегают к помощи аксонометрических проекций. Они бывают косоугольными (кабинетная проекция) и прямоугольными (изометрическая и диметрическая). Такие проекции дают наглядное и очень правильное изображение предмета и оказывают помощь верно осознать чертеж.
Большое значение имеют вспомогательные линии, каковые во многих случаях разрешают осознать чертеж без дополнительных проекций. Исходя из этого на проекциях тел вращения (шар, цилиндр, конус, параболоид и т. д.) и отверстий постоянно наносят осевые линии.
Не меньшую роль играются штриховые линии, обозначающие на чертежах невидимые с данной стороны элементы подробностей (отверстия, выступы, фаски и т. д.). Они отличаются лишь штриховыми линиями. А посмотрите, как отличаются друг от друга изображенные на них подробности. Как видите, на чертеже не бывает лишних линий. Любая из них имеет определенное назначение и оказывает помощь верно прочесть чертеж.
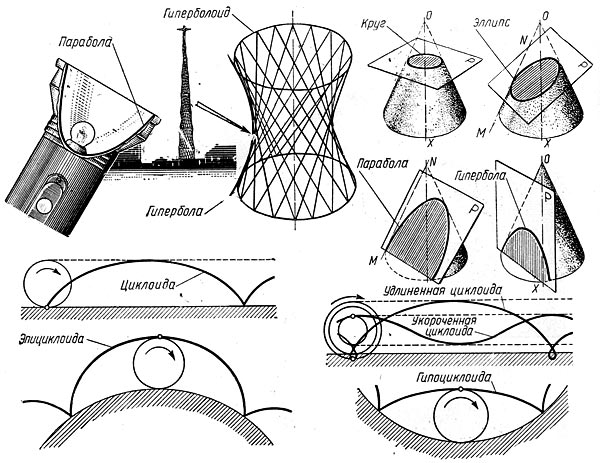
В черчении видятся разные закономерные кривые, и для каждой из них имеется собственные методы построения.