энтропия и Информация
Обсуждая понятие информация, нереально не затронуть второе смежное понятие – энтропия[1]. В первый раз понятия информация и энтропия связал К.Шеннон.

|
Клод Элвуд Шеннон (Claude Elwood Shannon), 1916-2001 — дальний родственник Томаса Эдисона, математик и американский инженер, был сотрудником Bell Laboratories с 1941 дo 1972 г. В его работе Математическая теория связи (http://cm.bell-labs.com/cm/ms/what/shannonday/), размещённой в 1948 г., в первый раз определялась мера информационного содержания любого сообщения и понятие кванта информации — бита. Эти идеи легли в базу теории современной цифровой связи. Вторая работа Шеннона Communication Theory of Secrecy Systems, размещённая в 1949 г., содействовала превращению криптографии в научную дисциплину. Он есть основателем теории информации, отыскавшей использование в современных высокотехнологических совокупностях связи. Шеннон внес громадный вклад в теорию вероятностных схем, теорию систем и теорию автоматов управления — науки, объединяемые понятием «кибернетика». |
Физическое определение энтропии
В первый раз понятие энтропии ввел Клаузиус в 1865 г. как функцию термодинамического состояния совокупности
S = Q/T,
где Q – теплота, T — температура.
Физический суть энтропии проявляется как часть внутренней энергии совокупности, которая не может быть перевоплощена в работу. Клаузиус эмпирически взял эту функцию, экспериментируя с газами.
Л.Больцман (1872г.) способами статистической физики вывел теоретическое выражение энтропии
S = K lnW,
где К – константа; W – термодинамическая возможность (количество перестановок молекул совершенного газа, не воздействующее на макросостояние совокупности).
Энтропия Больцмана выведена для совершенного газа и трактуется как мера беспорядка, мера хаоса совокупности. Для совершенного газа энтропии Больцмана и Клаузиуса тождественны. Формула Больцмана стала такой знаменитой, что начертана в качестве эпитафии на его могиле. Сложилось мнение, что хаос и энтропия имеется одно да и то же. Не обращая внимания на то, что энтропия обрисовывает лишь совершенные газы, ее некритично стали привлекать для описания более сложных объектов.
Сам Больцман в 1886г. постарался посредством энтропии растолковать, что такое жизнь. Согласно точки зрения Больцмана, жизнь это явление, талантливое уменьшать собственную энтропию. В соответствии с Больцману и его последователям, все процессы во Вселенной изменяются в направлении хаоса. Вселенная идет к тепловой смерти. Данный мрачный прогноз продолжительно господствовал в науке. Но углубление знаний об окружающем Мире понемногу расшатали эту догму.
Классики не связывали энтропию с информацией.
Энтропия как мера информации
Увидим, что понятие информация довольно часто трактуется как сведения, а передача информации осуществляется посредством связи. К. Шеннон разглядывал энтропию как меру нужной информации в процессах передачи сигналов по проводам.
Для расчета энтропии Шеннон внес предложение уравнение, напоминающее хорошее выражение энтропии, отысканное Больцманом. Рассматривается свободное случайное событие x с N вероятными состояниями и pi—возможность i-го состояния. Тогда энтропия события x
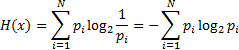
Эта величина кроме этого именуется средней энтропией. К примеру, обращение может идти о передаче сообщения на естественном языке. При передаче разных букв мы передаем различное количество информации. Количество информации на букву связано с частотой потреблений данной буквы во всех сообщениях, формируемых на языке. Чем более редкую букву мы передаем, тем больше в ней информации.
Величина
Hi = Pi log2 1/Pi = ?Pi log2 Pi,
именуется личной энтропией, характеризующей лишь i-e состояние.
 Поясним на примерах. При бросании монеты выпадает орел либо решка[2], это определенная информация о итогах бросания.
Поясним на примерах. При бросании монеты выпадает орел либо решка[2], это определенная информация о итогах бросания.
Для монеты число равновероятных возможностей N = 2. Возможность выпадения орла (решки) равна 1/2.
1
При бросании кости приобретаем данные о выпадении определенного количества очков (к примеру, трех). В каком случае мы приобретаем больше информации?
Для кости число равновероятных возможностей N = 6. Возможность выпадения трех очков кости равна 1/6. Энтропия равна 2.58. Реализация менее возможного события дает больше информации. Чем больше неопределенность до получения сообщения о событии (бросание монеты, кости), тем большее количество информации поступает при получении сообщения.
Таковой подход к количественному выражению информации далеко не универсален, т. к. принятые единицы не учитывают таких ответственных особенностей информации, как ее смысл и ценность. Абстрагирование от конкретных особенностей информации (суть, сокровище ее) о настоящих объектах, как в будущем выяснилось, разрешило распознать неспециализированные закономерности информации. Предложенные Шенноном для измерения количества информации единицы (биты) пригодны для оценки любых сообщений (рождение сына, результаты спортивного матча и т. д.). В будущем делались попытки отыскать такие меры количества информации, каковые учитывали бы ее смысл и ценность. Однако тут же терялась универсальность: для различных процессов разны критерии смысла и ценности. Помимо этого, ценности информации и определения смысла субъективны, а предложенная Шенноном мера информации объективна. К примеру, запах несет огромное количество информации для животного, но неуловим для человека. Ухо человека не принимает ультразвуковые сигналы, но они несут довольно много сведений для дельфина и т. д. Исходя из этого предложенная Шенноном мера информации пригодна для изучения всех видов информационных процессов, независимо от вкусов потребителя информации.
Измерение информации
Из курса физики вы понимаете, что прежде, чем измерять значение какой-либо физической величины, нужно ввести единицу измерения. У информации также имеется такая единица — бит, но суть ее разен при различных подходах к определению понятия “информация”.
Существует пара различных подходов к проблеме измерения информации.