Приложение В
| Продолжение табл, Б.2.2 | |||||
| Ю L | Ю 9 | ||||
| . 10 | |||||
| И | |||||
| И | И | ||||
| !2 | |||||
| П | |||||
| Средняя | 13,4 | 12,7 | Средняя | 14,06 | 17,9 |
| Стандарт- | Стандарт- | ||||
| ное от- | шнобель от- | ||||
| клонение | 2,29 | 2,09 | клонение | 2,28 | 2,97 |
| Девушки: Д1-Д14 | т Юноши: Ю1\Ю16 | ||||
Описательная статистика
Описательная статистика разрешает обобщать первичные результаты, полученные при наблюдении либо в опыте. Процедуры тут сводятся к группировке данных по их значениям, построению распределения их частот, обнаружению центральных тенденций распределения (к примеру, средней арифметической) и, наконец, к оценке разброса данных по отношению к отысканной центральной тенденции.
Группировка данных
Для группировки нужно в первую очередь расположить эти каждой выборки в возрастающем порядке. Так, в отечественном опыте для переменной «число пораженных мишеней» эти будут размешаться следующим образом:
| Умелая несколько (дополнить цифрами} | |||||||||||||||||
| Фон:………………. *……………•. — •…… | |||||||||||||||||
| Пост действия; …..,.,,,,*…,.;,,,……..м…….. *……… | |||||||||||||||||
| Контрольная несколько | |||||||||||||||||
| Фон: | |||||||||||||||||
| По окончании voatintCTBMif: |
обработка и Статистика Данных 283
Распределение частот (числа пораженных мишеней)
Уже при первом взоре не получение последовательности возможно подметить, что многие эти принимают одинаковые значения, причем одни значения видятся чаще, а вторые-реже. Исходя из этого было бы весьма интересно сначала графически представить распределение разных значений с учетом их частот. Наряду с этим приобретают следующие столбиковые диаграммы:
Контрольная несколько
По окончании действий (дополнить столбиками!
Умелая несколько
| 1Э | ?0 | |||||||||||||
| Фон |
По окончании действии {дополнить столбиками)
Такое распределение данных по их значениям дает нам уже значительно больше, чем представление в виде радов. Но подобную группировку применяют по большей части только для качественных данных, четко разделяющихся на обособленные категории (см. дополнение Б. I),
Что касается количественных данных, то они постоянно располагаются на постоянной шкале и, в большинстве случаев, очень бессчётны. Исходя из этого такие эти предпочитают собирать по классам, дабы яснее видна была главная тенденция распределениям
Такая группировка пребывает в основном в том, что объединяют эти с однообразными либо родными значениями в классы и определяют частоту для каждого класса. Метод разбиения на классы зависит от того, что именно экспериментатор желает распознать при разделении измерительной шкалы на равные промежутки. К примеру, в нашем случае возможно сгруппировать эти по классам с промежутками в две либо три единицы шкалы:
| X | • | X | ||||||||||||||||||||||||||||||||||||||||||||||||||
| X | X | X | X | |||||||||||||||||||||||||||||||||||||||||||||||||
| X | X | X | X | X | х | X | X | X | ||||||||||||||||||||||||||||||||||||||||||||
| ?2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фом | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| (У | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| л. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Приложение | Б | |||||||||||||
| Контрольная групп* | ||||||||||||||
| X | ||||||||||||||
| X | X | |||||||||||||
| X | X | ж | ||||||||||||
| X | X | X | X | X | X | |||||||||
| X | X | х | X | X | X | X | ||||||||
| X X | X | X | * х | X | X | X X | ||||||||
| Клксы | 10-11 | 12-13 | 14 15 | ieir | 13-19 | 20-21 | гг-га | 9-1 | 12-14 | 15-17 | 16-го | 21-23 | ||
| Частоты | е | э | г | А | ||||||||||
| Фон | Фан | |||||||||||||
| (с промежутками в 2 ъд.\ | (с промежутками в, 3 вд,} |
(заполнить таким же образом)
_
Выбор того либо иного типа группировки зависит от разных мыслей. Так, в нашем случае группировка с промежутками между классами в две единицы отлично выявляет распределение результатов около центрального «пика». Одновременно с этим группировка с промежутками в три единицы владеет тем преимуществом, что дает более обобщенную и упрощенную картину распределения* особенно в случае, если учесть, что число элементов в каждом классе мало1. Конкретно исходя из этого в дальней* шем мы будем оперировать классами в три единицы.
Умелая групп*
| Классы | в-10 | |||||
| Частоты | ||||||
| Фон | ||||||
| Классы | 5-7 | |||||
| Частоты |
По окончании действий (с промежутками в 3 не сильный.)
Эти, разрушенные на классы по постоянной шкале, нельзя представить графически так, как это сделано выше. Исходя из этого предпочитают
1 При солидном количестве данных число классов по возможности должно быть где-то в пределах от 10 ло 20, с промежутками до 10 и более.
| Классы | а-э | |||||||||||||
| Частоты | ||||||||||||||
| • | По окончании действия {с промежутками в 2 ед.) | По окончании действия (с промежутками в 3 ед-1 |
_____________Статистика и обработка данных____________285
применять так именуемые гистограммы-метод графического
представления в виде примыкающих друг к другу прямоугольников:
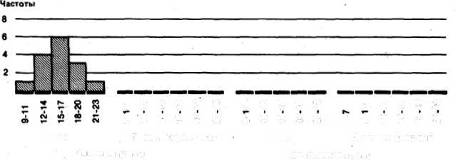
Фон Покушал* действия Фон По окончании действия
Умелая несколько Контрольная групп*
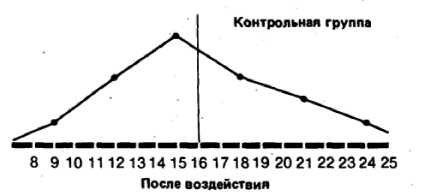
Наконец, для еще более наглядного представления неспециализированной конфигурации распределения возможно сооружает полигоны распределения частот. Для этого отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а после этого с обеих сторон «замыкают» площадь под кривой, доводя финиши полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения. Наряду с этим приобретают следующую картину:
Частоты
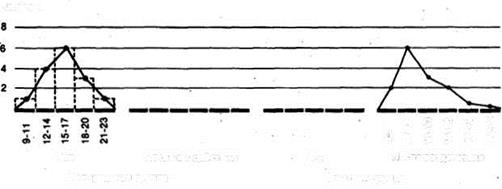
Контрольная несколько Умелая несколько
В случае, если сравнить полигоны, к примеру, для фоновых (исходных) значений контрольной значений и группы по окончании действия для умелой группы, то возможно будет заметить, что в первом случае полигон практически симметричен (т. е, в случае, если сложить полигон в два раза по вертикали, проходящей через его середину, то обе половины наложатся друг на друга)* в то время как для экспериментальной группы он асимметричен и смещен влево (так что справа у него как бы вытянутый шлейф).
Полигон для фоновых данных контрольной группы относительно близок к совершенной кривой, которая имела возможность бы оказаться для вечно громадной популяции. Такая кривая -кривая обычного распределения -имеет колоколообразную форму я строго симметрична. В случае, если же количество данных ограничено (как в выборках, применяемых для научных изучений), то в лучшем случае приобретают только некое приближение (аппроксимацию) к кривой обычного распределения.
Приложение f
Если вы выстроите полигон для фоновых значений умелой значений и группы по окончании действия для контрольной группы, то вы точно увидите, что так же будет обстоять дело и в этих обстоятельствах.
Оценка центральной тенденции
В случае, если распределения для контрольной группы и для фоновых значений в умелой группе более либо. менее симметричны, то значения, приобретаемые в умелой группе по окончании действия, группируются, как уже говорилось, больше в левой части кривой. Это показывает, что по окончании потребления марихуаны выявляется тенденция к ухудшению показателей у солидного числа испытуемых.
Чтобы выразить подобные тенденции количественно, применяют три вида показателей моду, медиану и среднюю.
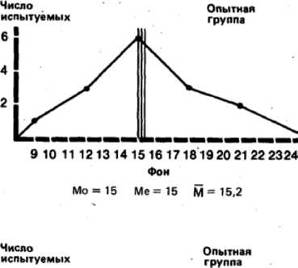
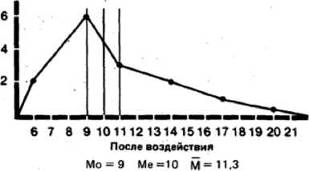
1. Мода (Мо)-это самый простой из всех трех показателей. Она соответствует или самоё частому значению, или среднему значению класса с громаднейшей частотой. Так, в отечественном примере для экспериментальной группы мода для фона будет равна 15 (результат видится четыре раза и находится в середине класса 14-15-16), а по окончании действия (середина класса 8-910),
Мода употребляется редко и в большинстве случаев чтобы дать неспециализированное представление о распределении. В некоторых случаях у распределения смогут быть две моды; тогда говорят о бимодальном распределении. Такая хартина показывает на то что в данном совокупности имеются две довольно независимые группы (см,, к примеру, эти Триона, приведенные в документе 3.5).

Бимодальное распределение
*
2, Медиана (Me) соответствует центральному значению в последовательном последовательности всех взятых значений. Так, для фона в экспериментальной группе, где мы имеем последовательность
10 11 12 13 14 14 15 15 15 15 17 17 19 20 21,
медиана соответствует 8-му значению, т.е. 15. Для результатов действия в экспериментальной группе она равна 10.
Если число данных п, четное, медиана равна средней арифметической между значениями, находящимися в раду на л/2-м и я/2 + 1-м местах. Так, для- результатов действия для восьми юношей умелой группы медиана находится между значениями, находящимися на 4-м (8/2 = 4) и 5-м местах в последовательности. В случае, если выписать целый
обработка и Статистика данных
2У7
последовательность для этих данных;, то есть
7 8 9 II 12 13 14 16,
то окажется, что медиана соответствует (II + 12)/2 =11,5 (видно, что медиана не соответствует тут ни одному из взятых значений),
3. Средняя арифметическая (1Й) (потом легко «средняя») — это чаще всего применяемый показатель центральной тенденции. Ее используют, например, в расчетах, нужных для описания распределения и для его предстоящего анализа. Ее вычисляют t поделив сумму всех значений данных на число этих данных. Так, для отечественной умелой группы она составит- 15,2(228/15) для фона и 11,3(169/15) для результатов действия.
В случае, если сейчас отметить все эти три параметра на каждой из кривых для экспериментальной группы, то будет видно, что при обычном распределении они более либо менее совпадают, а при асимметричном расп ред е л е ни и — нет.
Перед тем как идти дальше, полезно будет вычислить все эти показатели для обеих распределений контрольной группы-они понадобятся нам в будущем: . .
Приложение Б
Оценка разброса
Как мы уже отмечали, темперамент распределения результатов по окончании действия изучаемого фактора в умелой группе дает значительную данные о том, как испытуемые делали задание. Сообщённое относится и к обоим распределениям в контрольной группе:
Контрольная несколько Мода (Мо) Мели* не (Me) Средни а (м)
| Фон: …………….. |
| По окончании действия: ч • — •:……. • •……• • ,…••.«••-. |
Сходу кидается в глаза, что в случае, если средняя и в том и другом случае практически однообразна, то во втором распределении результаты больше разбросаны, чем в первом, В таких случаях говорят, что у второго распределения больше диапазон, либо размах вариаций, т.е, отличие между большим и минимальным значениями.
Так, в случае, если забрать контрольную группу, то диапазон распределения для фона составит 22 — 10 = 12, а по окончании действия 25 — 8 — 17. Это разрешает высказать предположение, что повторное исполнение задачи на глазодвигательную координацию оказало на испытуемых из контрольной группы определенное влияние; у одних показатели улучшились, у других ухудшились1. Но для количественной оценки разброса результатов
1 Тут имел возможность проявиться эффект плацебо связанный с тем, что запах дыма травы позвал у испытуемых уверенность в том, что они находятся под действием наркотика. Для проверки этого предположения следовало бы повторить опыт со второй контрольной группой, в которой испытуемым будут давать лишь простую сигарету.

u /lOfHtonmKit thmiwx
довольно средней в том либо другом распределении существуют более правильные способы, чем измерение диапазона.
Значительно чаще для оценки разброса определяют отклонение каждого из взятых значений от средней (М-М) обозначаемое буквой d, а после этого вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Наоборот, в случае, если эта средняя мала, то эти больше сконцентрированы довольно их среднего значения и выборка более однородна.
Итак, первый показатель, применяемый для оценки разброса,-это среднее отклонение. Его вычисляют следующим образом (пример, что мы тут приведем, не имеет ничего общего с нашим гипотетическим опытом). Собрав все сведенья и расположив их в ряд
3 5 6 9 11 14,
находят среднкУю арифметическую для выборки:
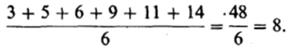
После этого вычисляют отклонения каждого значения от средней и суммируют их:
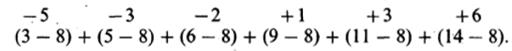
Но при таком сложении отрицательные и хорошие отклонения будут уничтожать друг друга, время от времени кроме того абсолютно, так что итог (как в данном примере) может оказаться равным нулю. Из этого ясно, что необходимо обнаружить сумму безотносительных значений личных отклонений и уже эту сумму дробить на их неспециализированное число. Наряду с этим окажется следующий итог:
среднее отклонение равняется
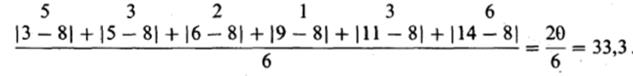
Неспециализированная формула:

где (сигма) свидетельствует сумму; \d\- безотносительное значение каждого личного отклонения от средней; «-число данных.
Но безотносительными значениями достаточно тяжело оперировать в алгебраических формулах* применяемых в более сложном статистическом анализе. Исходя из этого статистики решили пойти по «обходному пути», разрешающему отказаться от значений с отрицательным знаком, то есть возводить все значения в квадрат, а после этого дробить сумму квадратов на
19-443
flfHLtlKXCVIttlC Л
число данных. В отечественном примере это выглядит следующим образом:
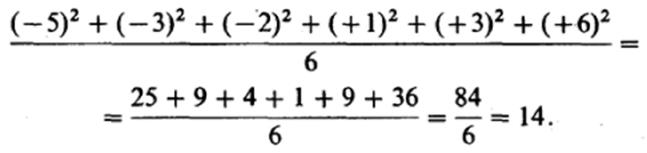
В следствии для того чтобы расчета приобретают так именуемую варианеу1* Формула для вычисления вариансы, так, следующая:
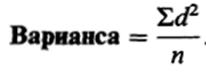
Наконец, для получения показателя, сопоставимый по величине со средним отклонением, статистики решили извлекать из вариансы квадратный корень. Наряду с этим получается так именуемое стандартное отклонение:

В отечественном примере стандартное отклонение равняется 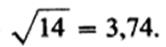
направляться еще добавить* что чтобы более совершенно верно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем нужно применять не /г, а п — 1:
—
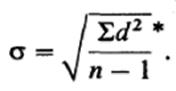
Возвратимся сейчас к нашему опыту и посмотрим, как нужен выясняется данный показатель для описания выборок.
На первой стадии, очевидно, нужно вычислить стандартное
Г
1 Варнанса представляет собой один из показателей разброса, применяемых в некоторых статистических методиках (к примеру, при вычислении критерия F; см, следующий раздел). направляться подчернуть, что в отечественной литературе варианту довольно часто именуют дисперсией.-Прим. rtepee.
* Стандартное отклонение для популяции обозначается маленькой греческой буквой сигма 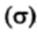 , а для выборки — буквой s. Это относится и вариансы, т.е. квадрата стандартного отклонения: для популяции она обозначается
, а для выборки — буквой s. Это относится и вариансы, т.е. квадрата стандартного отклонения: для популяции она обозначается 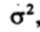 , а для выборки —
, а для выборки —
tt vtipafwniKct
отклонение для всех четырех распределений. Сделаем это сперва для фона умелой группы:
Расчет стандартного отклонения1 для фона контрольной группы
Испытуемые Число пора* Средняя женных мише-ней в серии
Отклоне- Квадрат от-
кие от клонздия от
средней (*/) средней (dl)
| 2 3 | 10 12 • | 15,8 15,8 15,8 | -ЗД + 5,8 + 3,8 | 10,24 33,64 14,44 |
| — | — | — 15,8 | -6,2 | г 38,44 |
Сумма
Стандартное отклонение
1 Формула для расчетов н сами расчеты приведены тут только в качестве иллюстрации. В наши дни значительно несложнее при об* рести таковой карманный микрокалькулятор, в котором подобные расчеты уже заблаговременно запрограммированы, и для расчета стандартного отклонения достаточно только ввести эти, а после этого надавить клавишу s.
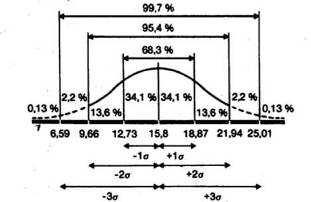
О чем же свидетельствует стандартное отклонение, равное 3,07? Выясняется, оно разрешает заявить, что большинство результатов (выраженных тут числом пораженных мишеней) находится в пределах 3,07 от средней, т.е. между 12,73 (15,8 — 3,07) и 18,87 (15,8 4- 3,07),
Чтобы лучше осознать, что подразумевается под «большей частью результатов», необходимо сперва разглядеть те свойства стандартного отклонения, каковые проявляются при изучении популяции с обычным распределением.
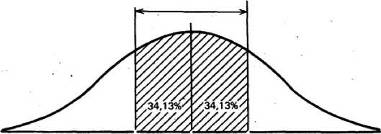
Статистики продемонстрировали, что при обычном распределении «большинство» результатов, располагающаяся в пределах одного стандартного отклонения по обе стороны от средней, в процентном отношении в любой момент одинаковая и не зависит от величины стандартного отклонения: она соответствует 68% популяции (т, е. 34% ее элементов находится слева и 34%-справа от средней):

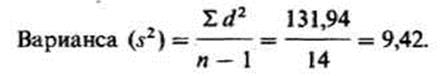
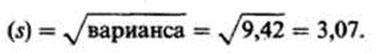
При.южеши* Б
6ЭГ27%
М-0 М М+о
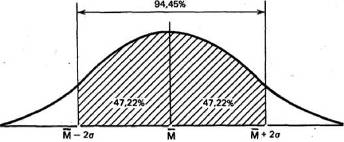
Совершенно верно гак же вычислили, что 94,45% элементов популяции при обычном распределении не выходит за пределы двух стандартных отклонений от средней:
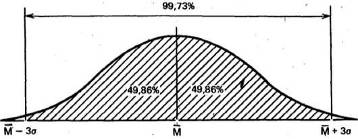
и что в пределах трех стандартных отклонений умещается практически вся популяция-99,73%.
Учитывая, что распределение частот фона контрольной группы достаточно близко к обычному, возможно считать, что 68% участников всец популяции, из которой забрана выборка, также будет получать сходные результаты, т,е, попадать приблизительно в 13-19 мишеней из 25, Распределение результатов остальных участников популяции должно выглядеть следующим образом;
Статистики tt обработка данных
Гипотетическая популяция,
из которой забрана контрольная несколько (фон)
Что касается результатов той же группы по окончании действия изучаемого фактора, то стандартное отклонение для них выяснилось равным 4,25 (пораженных мишеней). Значит, возможно высказать предположение, что 68% результатов будут размешаться конкретно в этом диапазоне отклонений от средней, составляющей 16 мишеней, т. е. в пределах от 11,75 (16 — 4,25) до 20,25 (16 + 4,25), либо, округляя, 12 — 20 мишеней из 25. Видно, что тут разброс результатов больше, чем в фоне. Эту отличие в разбросе между двумя выборками для контрольной группы возможно графически представить следующим образом:
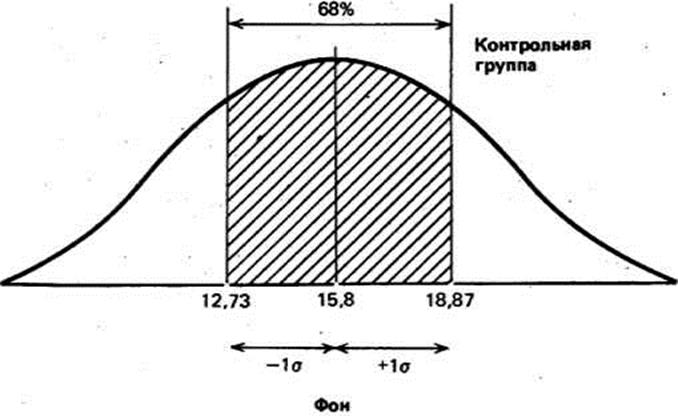
Приложение И
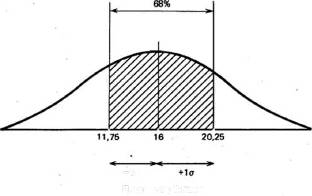
-t
По окончании действия
Потому, что стандартное отклонение постоянно соответствует одному и тому же проценту результатов, укладывающихся в его пределах около средней, возможно утверждать, что при любой форме кривой обычного распределения та часть ее площади, которая ограничена (с обеих сторон) стандартным отклонением, в любой момент однообразна и соответствует одной и той же доле всей популяции. Это возможно проверить на тех отечественных выборках, для которых распределение близко к обычному,-на информации о фоне для контрольной и умелой групп.
Итак, ознакомившись с описательной статистикой, мы определили» как возможно представить графически и оценить количественно степень разброса данных в том либо другом распределении. Тем самым мы смогли осознать, чем различаются в отечественном опыте распределения для контрольной группы до и по окончании действия. Но возможно ли о чем-то делать выводы по данной разнице-отражает ли она реальность либо же это легко артефакт, связанный со через чур малым количеством выборки? Тот же вопрос (лишь еще острее) поднимается и в отношении экспериментальной группы, подвергнутой действию свободной переменной. В данной группе стандартное отклонение для фона и по окончании действия также различается приблизительно на 1 (3,14 и 4,04 соответственно). Однако здесь особенно громадна отличие между средними-15,2 и 11,3* На основании чего возможно было бы утверждать, что эта разность средних вправду точна, т,е\ велика, дабы возможно было с уверенностью растолковать ее влиянием свободной переменной, а не несложной случайностью? В какой степени возможно опираться на эти результаты и распространять их на всю популяцию, из которой забрана выборка, т, е. утверждать, что потребление марихуаны и в действительности в большинстве случаев ведет к нарушению глазодвигательной координации? —