Определение 5. Пускай множество в , и каждой точке поставлено в соответствие единственное настоящее число . В этом случае говорят, что на множестве Х выяснена числовая функция n переменных либо функция нескольких переменных.
Правило, по которому устанавливается соответствие, обозначают некоей буквой, к примеру и пишут
либо , .
Вторыми словами функция n переменных имеется отображение множества на множество :
, где .
Множество Х есть областью определения функции , а именуют доводом либо свободной переменной. Функция именуется элементарной, если она задана посредством конечного числа арифметической операции и суперпозиций элементарных функций одной переменной.
Определение 6. Графиком функции именуют множество точек связанных соотношением .
Примеры. 1) Функция есть линейной функцией n переменных и называетсягиперплоскостью. Область определения её все точки, находящиеся в собствености .
2) Функция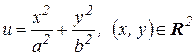 
именуется эллиптическим параболоидом. В случае, если a=b, то это параболоид вращения.Область определения ее множество (нарисовать график).
3) Для функции область определения получается из условия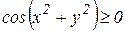 
. Откуда направляться, что выполнятся неравенства 
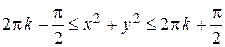( . Так, областью определения являются концентрические кольца с центром в начале координат.
4) Функция n-переменных
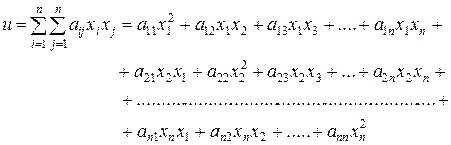
именуется квадратичной формой (квадратичная функция n переменных).
Пускай определяется на и имеется предельная точка множества Х.
Определение 7 (О.Л. Коши 1789-1857 фр.). Число именуется пределом функции в , в случае, если для любого хорошего возможно указать положительное число такое, что из исполнения условия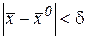 
для любого направляться исполнение неравенства .
Это определение символически возможно записать следующим образом:
: .
Определение 8. (Г.Э.Гейне 1821-1881 нем.). Число именуется пределомв точке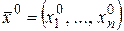 
, в случае, если , сходящейся к направляться, что последовательность 
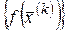сходится к .
Как и для функции одной переменной доказывается, что определения 7 и 8 равносильны. Предел функции многих переменных обозначается
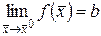либо 
.
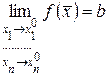Пример. Отыскать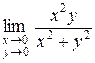 
.
Ответ. Докажем, что предел равен 0. Выберем , заберём , такое, что , удовлетворяющих условию и хороших от начала координат справедливо неравенство:
. 
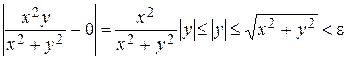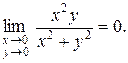
Для пределов функций нескольких переменных честны следующие утверждения, подобные соответствующим теоремам для функций одной переменной.
• В случае, если имеет предел при , то он единственный.
•Критерий Коши. Чтобы имела конечный предел при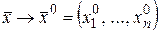 
нужно и достаточно, дабы , такое что для из исполнения услови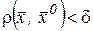й 
и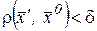 
следовало бы исполнение неравенства .
• Пускай и функции с неспециализированной областью определения и существуют пределы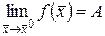 
и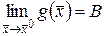 
. Тогда существуют пределы функций , и 
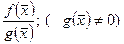и имеют место равенства: , 
, 
, .
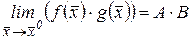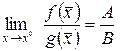Определение 9. Число именуется пределом функциипри , в случае, если и записывается .
Определение 10. Пускай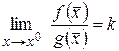 
и , при . В случае, если , то и именуются вечно малыми одного порядка при . В случае, если , то функции и именуются эквивалентными при . В случае, если , то функция именуется вечно малой более большого порядка по отношению к .
Определение 11. Число именуют пределом функции по множеству в точке, в случае, если , такое что для произвольного из исполнения условия направляться . Обозначение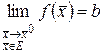 
.
Это обобщение предела функции в точке, на тот случай, в то время, когда функция рассматривается не во всей окрестности точки , а на некоей ее части.
В случае, если имеется постоянная кривая Г, проходящая через точку , то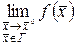 
именуют пределом по кривой Г.
В частности, в случае, если Г – имеется прямая линия с направленным единичным вектором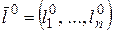 
, 
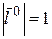, то предел по Г именуют пределом по направлению вектора .
Для функции n-переменных при возможно разглядывать n, так именуемые, повторные пределы. В частности для функции двух переменных возможно разглядывать два повторных предела в точке :
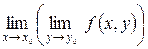и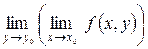 
.
В случае, если оба повторных предела существуют, то они не обязательно равны между собой.
Пример. Отыскать предел функции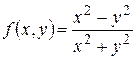 
в точке .
Ответ.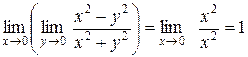 
.
.
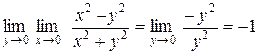Теорема 3. В случае, если функция выяснена в , , за исключением возможно самой точки , существует предел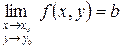 
и существуют пределы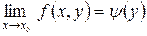 
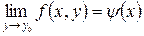, тогда существуют и повторные пределы 
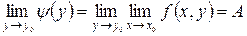и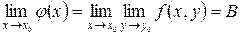 
, каковые равны между собой и равны : .
? По определению предела функции двух переменных имеем, что существует , такое что, в случае, если , другими словами . Из этого следует, что . Переходя к пределу в этих неравенствах при , возьмём, что при имеет место неравенство . Из этого следует, что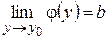 
.
Так,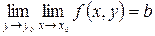 
. Подобно доказывается, что 
.
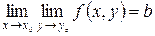Пускай выяснена на .
Определение 12. Функция именуют постоянной в точке , в случае, если – предельная точка множества X; – выяснена в точке и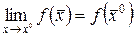 
.
На языке « » последнее свидетельствует, что , такое, что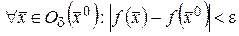 
.
Иначе говоря в случае, если , то тогда
.
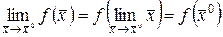Если не есть постоянной в точке , то она именуется разрывной в данной точке, а точку именуют точкой разрыва. Возможно доказать, что любая элементарная функция есть постоянной в каждой точке, в которой она выяснена.
Примеры.1) Изучить функцию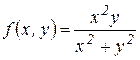 
на непрерывность.
Ответ. Функция везде выяснена и постоянна, не считая точки . Ранее было продемонстрировано, что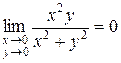 
. Тогда точка (0, 0) есть точкой устранимого разрыва, т.к. неизвестна, но предел существует и равен 0. В случае, если доопределить , то возьмём постоянную функцию.
2) Изучить функцию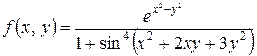 
на непрерывность.
Ответ. Функции и постоянны при всех как многочлены. По теореме о непрерывности суперпозиции постоянных функций вытекает, что и постоянны. Так как при любых значениях и , то постоянна.
Определение 13. Функция именуется постоянной намножестве , если она постоянна в каждой точке этого множества.
Как и для функций одной переменной честны следующие утверждения.
• В случае, если функции и выяснены на множестве и постоянны в точке , то в выяснены и постоянны функции , , .
• В случае, если выяснена и постоянна в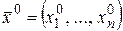 
, тогда существует окрестность точки , в которой выполняется условие . Это указывает, что функция ограничена в окрестности данной точки.
• В случае, если выяснена и постоянна в точке и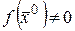 
, то существует такая окрестность данной точки, в которой сохраняет символ.
• В случае, если функции , , …, постоянны в точке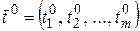 
, а функция постоянна в точке 
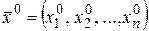, где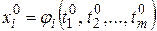 
, , то сложная функция постоянна в точке .
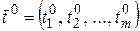Эти теоремы доказываются так же, как теоремы для функций одной переменной.Честна кроме этого теорема.
Теорема 4 (Коши о прохождении постоянной функции через любое промежуточное значение). Пускай постоянна на линейно-связанном множестве , причем и значения в точках , а такое, что . Тогда на любой постоянной кривой Г, соединяющей точки и , полностью принадлежащей Х существует такая точка , что .
? Пускай , , …, , – параметрические уравнения кривой , соединяющей точки и из множества и . Тогда на отрезке выяснена сложная функция одной переменной , где . Разумеется, значение данной функции на отрезке совпадают со значениями на . По теореме о постоянной сложной функции она постоянна, а, следовательно, по теореме о прохождении промежуточных значений для функции одной переменной : . Исходя из этого в точке , координаты которой , , …, будет справедливо равенство .
Определение 14. Функция именуется равномерно-постоянной на множестве , в случае, если для любого хорошего найдется такое положительное число , что для и из множества Х таких, что при выполняется неравенство .
Это же определение на языке записывается следующим образом
.
Имеют место утверждения, подобные теоремам для функции одной переменной.
• В случае, если функция выяснена и постоянна на ограниченном замкнутом множестве , то ограничена на этом множестве (первая теорема Вейерштрасса).
• В случае, если функция выяснена и постоянна на ограниченном замкнутом множестве , то достигает на правильных верхней и нижней граней, т.е.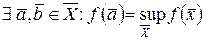 
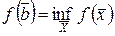(вторая теорема Вейерштрасса).
• В случае, если функция выяснена и постоянна на ограниченном замкнутом множестве , то равномерно постоянна на множестве (теорема Кантора).