Второе начало термодинамики равно как и первое результат обобщения обширного опыта и, следовательно, опирается на громадный фактический материал.
Существует много эквивалентных формулировок второго начала термодинамики. Приведем кое-какие из них:
1. Теплота не имеет возможности переходить от холодного тела к тёплому сама собой, даровым методом (Р. Клаузиус, 1850 г.).
2. Нереально создать вечный двигатель второго рода.
Под вечным двигателем второго рода подразумевается такая иногда действующая тепловая машина, которая была бы способна абсолютно превращать теплоту в работу, т.е. без передачи части ее холодильнику (В. Оствальд).
3. Громаднейший коэффициент нужного действия (h) тепловой автомобили не зависит от вида и природы рабочего тела (пар, газ, воздушное пространство и т. д.), а определяется лишь промежутком температур между холодильником и теплоисточником (теорема Карно — Клаузиуса). Математическое выражение теоремы Карно — Клаузиуса для квазистатических (равновесных) процессов.
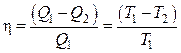
где h — коэффициент нужного действия тепловой автомобили для равновесных процессов, КПД;
Q1 -количество теплоты, переданное рабочему телу теплоисточником при температуреT1;
Q2 — количество теплоты, переданное рабочим телом холодильнику при Т2.
Преобразуя данное уравнение:
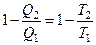либо 
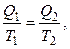
возможно представить в виде алгебраической суммы:
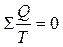
Для бесконечно малого обратимого цикла Карно:
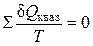
В пределе эта сумма возможно заменена интегралом по замкнутому контуру:
.
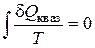В случае, если интеграл по замкнутому контуру от функции, равен нулю, то подинтегральное выражение есть функцией состояния. Клазиус назвал эту функцию энтропией (S). Следовательно:
.
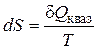В необратимом самопроизвольном ходе постоянно встретятся утраты на трение, на рассеяние тепла и т.д. В таких процессах КПД тепловой автомобили (h¢) в любой момент меньше, чем КПД тепловой автомобили в обратимых процессах (h), т.е. . Так, второй закон термодинамики для обратимых и необратимых процессов в дифференциальной форме возможно представлен в виде:
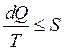либо
В соответствии с 1-му закону термодинамики . Подставляя значениеdQ в (33) возьмём фундаментальное уравнение термодинамики, объединяющее оба закона:
(34)
В случае, если совокупность будет выполнять работу лишь против сил внешнего давления, тогда и уравнение примет вид:
(35)
Из (35) направляться, что энтропия есть функцией от U и V.
Расчетные формулы энтропии
Часто понятие энтропии употребляется в качестве меры деградации (рассеяния) энергии. Чем больше энтропия, тем большинство энергии рассеивается в окружающее пространство, не преобразовываясь в нужную работу.
Следовательно, энтропия есть мерой ненужной теплоты, мерой обесцененной энергии, которая не может быть перевоплощена в нужную работу. Она есть мерой неупорядоченности состояния совокупности и растет не только с увеличением температуры, но и при плавлении жёсткого вещества, при кипении жидкости, т.е. при переходе вещества из состояния с меньшей энергией в состояние с большей энергией. Ростом энтропии сопровождаются такие процессы, как расширение газа, растворение кристаллов, и химические процессы, протекающие с повышением количества либо с повышением числа частиц, в то время, когда возрастает неупорядоченность совокупности.
Напротив, все процессы, которые связаны с упорядоченностью совокупности — охлаждение, конденсация, кристаллизация, сжатие, химические реакции, протекающие с уменьшением количества, числа частиц (к примеру, полимеризация), — сопровождаются уменьшением энтропии.
Энтропия — экстенсивное свойство совокупности. Она зависит от массы. В случае, если массу совокупности расширить в n раз, то и элементарное количество энтропии dSувеличится в n раз:
либо .
Как всякое экстенсивное свойство, энтропия владеет аддитивностью. Это указывает, что энтропия совокупности равна сумме энтропий составных частей.
Энтропия пропорциональна массе, ее величина возможно отнесена к разному количеству вещества. Значительно чаще эту величину относят к молю либо грамму вещества.
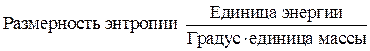сходится с размерностью теплоемкости, но из всего, что было сказано не нужно аналогия их физического значения.
Теплоемкость характеризует количество теплоты, нужное для нагревания тела на 1 градус.
Энтропия же характеризует количество рассеянной энергии, отнесенное к 1 градусу данной температуры.
Итак, энтропия есть функцией, определяющей направление протекающего процесса в изолированной совокупности:
- в случае, если в изолированной совокупности процесс сопровождается повышением энтропии, то он есть самопроизвольным,
- в случае, если в изолированной совокупности процесс сопровождается уменьшением энтропии , то он есть несамопроизвольным,
- в случае, если в изолированной совокупности энтропия не изменяется , это значит, что совокупность будет в состоянии равновесия.
Вычисление энтропии
Изобарный процесс ( ). В соответствии с (5) .
Т.к.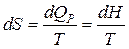 
, но , следовательно, 
.
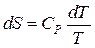Интегрируя, возьмём:
, 
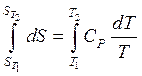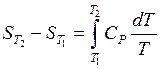. (36)
Под Т1 подразумевается каждая температура, меньшая, чем Т2.
Интегрирование левой части уравнения (36) возможно осуществлять при различных условиях:
1) в случае, если теплоемкость не зависит от температуры, тогда итог интегрирования возможно представлен в виде
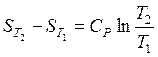либо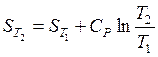 
. (37)
2) в случае, если теплоемкость зависит от температуры и эта зависимость выражается степенным рядом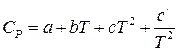 
, то результаты интегрирования примут вид:
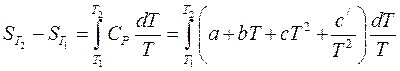. (38)
В соответствии с постулату Планка энтропия чистых жёстких веществ, образующих совершенные кристаллы, при полном нуле, равна нулю. Учитывая данный постулат, возможно выяснить полное значение энтропии химически чистых веществ в любом агрегатном состоянии и при любых температурах по уравнению:
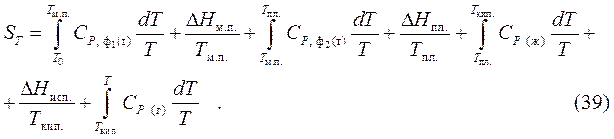
где – теплоемкость вещества в первой модификации,
– теплоемкость вещества во второй модификации,
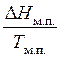— изменение энтропии при модификационном переходе,
, — теплоемкости вещества соответственно в жидком и газообразном состоянии,
, – изменение энтальпии вещества при испарении и плавлении соответственно,
, – кипения вещества и температуры плавления.
В общем виде:
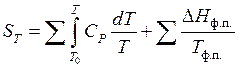(40)
где первая сумма высказывает изменение энтропии в ходе нагревания, а вторая изменение энтальпии при фазовых и модификационных переходах.
Для практических расчетов пользуются безотносительными значениями энтропии в стандартном состоянии при 298K, вычисленными при помощи постулата Планка.
Такую энтропию именуют стандартной и обозначают . Ее значения приведены в справочнике /5, табл.44; 6, табл.1/. В случае, если T1 в уравнении (38) равна 298, то оно принимает вид:
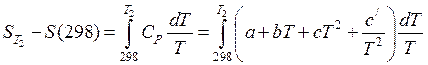(41)
Изменение энтропии в химических реакциях рассчитывают, используя первое следствие закона Гесса. К примеру, для реакции :
.
Пример 1. Вычислить энтропию реакции при 473К
Ответ. Для данного расчета, воспользовавшись первым следствием закона Гесса, запишем
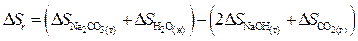
Используя уравнения (40) и (41), для отечественного случая возьмём:
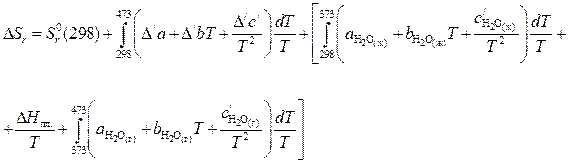
где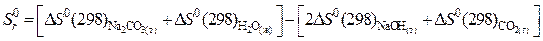 
.
Значение стандартных энтропий веществ находим в справочнике /5, табл.44/:
а) продукты реакции:
;
.
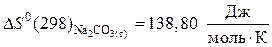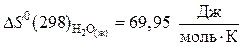б) исходные вещества:
,
,
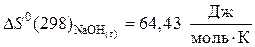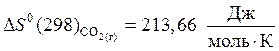определяем стандартную энтропию реакции:
.
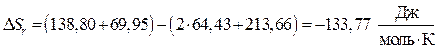Вывод: Изменение энтропии в стандартных условиях для данной реакции равняется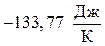 
, т.е. , следовательно в прямом направлении (слева направо) в этих условиях реакция не отправится.
Расчет коэффициентов D/а, D/b, D/c/ приведен в примере 2 раздела 1.4.2:
;
;
.
Изменение энтропии воды, имеющей в предложенном промежутке температур фазовый переход при Т = 373К, будем вычислять раздельно.
Значения коэффициентов а, b, c¢ для воды в жидком и газообразном состоянии находим в справочнике /5, табл.44/:
; ; ;
, , .
Подставив полученные данные в уравнение отечественного примера, возьмём:
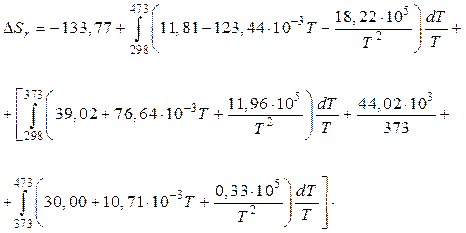
Проинтегрировав, возьмём
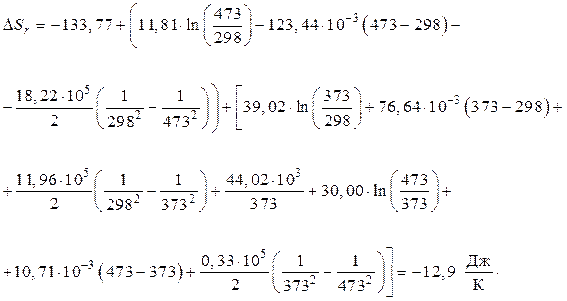
Вывод: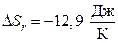 
. В отечественном примере с увеличением температуры энтропия возрастает, но ее значение близко к нулю. Это разрешает высказать предположение, что совокупность будет в состоянии, близком к равновесию.
- Изохорный процесс ( )
Расчет энтропии в изохорном ходе выполняют подобно расчету для изобарного процесса, лишь вместо изобарной теплоемкости употребляется изохорная теплоемкость CV :
, , 
.
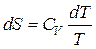Интегрируя в промежутке температур 298 — T, приобретаем:
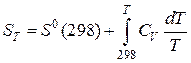. (42)
В случае, если CV не зависит от температуры, то по окончании интегрирования возьмём:
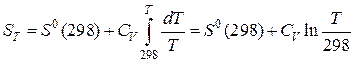. (43)
- Изотермический процесс ( )
Изотермические превращения происходят без трансформации внутренней энергии совокупности ( ), тогда из первого закона термодинамики:
.
В случае, если совокупность подчиняется законам совершенного газа, то из уравнения состояния совершенного газа Клапейрона — Менделеева:
,
где n — количество совершенного газа в молях,
R — универсальная газовая постоянная.
В следствии подстановки возьмём:
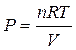, т.е. 
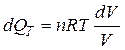, тогда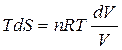 
либо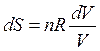 
(44)
Интегрируем полученное выражение в пределах S1 — S2 и V1 — V2:
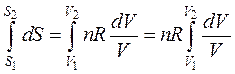
т.е.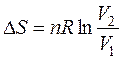 
(45)
либо пользуясь законом Бойля – Мариотта,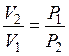 
, возможно записать:
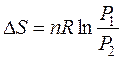(46)
Взятыми уравнениями (45) и (46) пользуются для ответа задач по изотермическому расширению газов, подчиняющихся законам совершенного газа.
Пример 2. Вычислить изменение энтропии при изотермическом расширении 1,7 моля совершенного газа, в случае, если V1 = 0,02м3, V2 = 2м3.
Ответ. Для расчета воспользуемся уравнением (45):
.
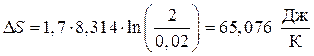Вывод. При изотермическом расширении совершенного газа в изолированной совокупности энтропия возрастает.
В случае, если изотермическим превращением есть изменение агрегатного либо модификационного состояния вещества при постоянном давлении, то изменение энтропии для одного моля соединения определяется по формуле:
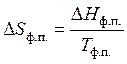, (47)
где — энтальпия фазового либо модификационного перехода,
— полная температура фазового либо модификационногоперехода.
Потому, что энтропия есть функцией состояния, то изменение энтропии возможно выяснить, в случае, если известно значение параметров начального и конечного состояний совокупности.
Пускай начальное состояние S1 характеризуется параметрами T1 и V1, а состояние S2 — параметрами T2 и V2 (в случае, если за свободные переменные выбраны T и V).Так как изменение энтропии не зависит от пути перехода, то эргономичнее разглядеть переход из состояния S1 в состояние S2, сперва изменяя температуру от T1 до T2 (при ), а после этого изменяя давление от V1 до V2 (при ). Суммируя изменение энтропии по этим двум процессам, приобретаем уравнение:
, 
.
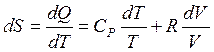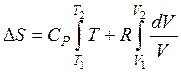По окончании интегрирования возьмём для совокупности, содержащей 1 моль совершенного газа:
а) в случае, если свободные переменные T и P, то
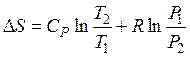; (48)
б) в случае, если свободные переменные T и V, то
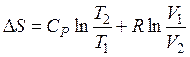. (49)
Пример 3. Отыскать изменение энтропии при изотермическом сжатии 1 моля паров бензола, при 800С от 0,4053?105 до 1,013?105 Па с охлаждением и последующей конденсацией жидкого бензола до 600С. Обычная температура кипения бензола 800С; молярная теплота испарения бензола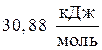 
; удельная теплоемкость жидкого бензола 
.
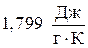Ответ. Этот процесс складывается из трех стадий:
1) изотермического сжатия паров бензола от 0,4053?105 до 1,013?105 Па;
2) конденсации паров бензола в жидкость при 800С;
3) охлаждения жидкого бензола от 80 до 600С.
Первая стадия. Процесс изотермический. Изменение энтропии рассчитывается по формуле (46)
.
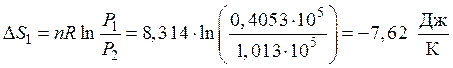Вторая стадия. Фазовый переход — также изотермический процесс. Изменение энтропии рассчитывается по формуле (47). Для одного моля бензола
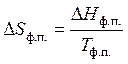, но , исходя из этого
.
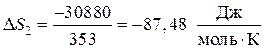Третья стадия. Процесс изобарный. Изменение энтропии рассчитывается по формуле (36). По условию задачи идет процесс охлаждения вещества, исходя из этого для разглядываемого случая формула (36) примет вид:
,
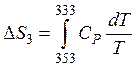где — молярная теплоемкость жидкого бензола.
В условии задачи дана удельная теплоемкость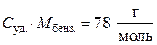 
, тогда:
.
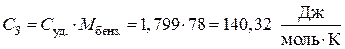Предположим, что молярная теплоемкость жидкого бензола в данных условиях не зависит от температуры.
Подставляя полученные значения CP и интегрируя в промежутке температур , возьмём:
.
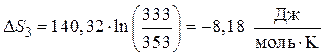Неспециализированное изменение энтропии в совокупности составит:
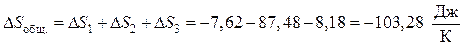
Вывод. Т.к. энтропия убывает, то рассмотренный процесс будет несамопроизвольный, т.е. в изолированной совокупности он неосуществим.
Так, были рассмотрены кое-какие уравнения, разрешающие вычислить трансформации энтропии по известным трансформациям параметров совокупности и по известным теплоемкостям.
Ранее подчеркивалось, что энтропия используется как критерий направленности процесса лишь для изолированных совокупностей, что затрудняет использование её на практике, где многие технологические процессы протекают либо при температуре и постоянном давлении в открытых реакторах, либо при температуре и постоянном объёме в закрытых реакторах. Но посредством энтропии возможно вычислить другие функции, каковые смогут выступить в направленности критерия процесса и роли равновесия. К таким функциям относятся энергия Гельмгольца (изохорно-изотермический потенциал) и энергия Гиббса (изобарно-изотермический потенциал).
1.5.4. Изохорно-изотермический потенциал (свободная энергия Гельмгольца)
Для вывода изохорно-изотермического потенциала воспользуемся объединенной формулой (34) 1-го и 2-го законов термодинамики для неравновесных и квазистатических процессов , которая показывает, что работа совокупности:
.
Процесс протекает при постоянном количестве, исходя из этого , тогда:
, (50)
U, T и S являются функциями состояния, следовательно, и выражение в скобках также будет функцией состояния. Ее и назвали свободной энергией Гельмгольца и обозначили F.
(51)
Из выражения (51) разумеется, что в изохорно-изотермическом ходе в работу переходит не вся внутренняя энергия, а лишь часть ее, остающаяся по окончании вычета TS из U.
Так, свободной энергией именуется та часть внутренней энергии совокупности, которая возможно перевоплощена в работу при постоянной температуре либо постоянном количестве.
Эта работа именуется нужной и в квазистатических процессах она будет большой.
Та часть внутренней энергии, которая не может быть перевоплощена в нужную работу (TS), именуется связанной либо ненужной энергией.
При протекании химической реакции единственным видом работы как правило есть работа расширения, т.е. , тогда:
либо .
Из взятого неравенства видно, какой процесс протекает в совокупности:
- в случае, если (энергия Гельмгольца убывает), то в совокупности протекает самопроизвольный процесс,
- в случае, если (энергия Гельмгольца не изменяется), то совокупность находится в равновесии,
- в случае, если (энергия Гельмгольца возрастает), то в совокупности протекает несамопроизвольный процесс.
Так, изохорно-изотермический потенциал есть критерием по определению направленности термодинамического процесса при свободных переменных — температуре и количестве.
Продифференцируем уравнение (51):
.
В случае, если учесть, что , то, подставляя dU, возьмём:
.
Приведем подобные члены:
. (52)
Из взятого уравнения находим:
а)в случае, если ,то
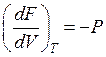. (53)
Вывод: давление есть мерой убыли свободной энергии совокупности с повышением количества при постоянной температуре;
б) в случае, если , то
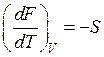. (54)
Вывод: энтропия есть мерой убыли свободной энергии совокупности с повышением температуры при постоянном количестве.
1.5.5. Изобарно-изотермический потенциал (энергия Гиббса)
Разглядим процессы, протекающие в совокупности при постоянном давлении либо температуре. Из уравнения (34) возьмём выражение для нужной работы:
,
но , тогда:
либо .
H, T и S являются функциями состояния, следовательно, и выражение в скобках также будет функцией состояния. Ее и назвали изобарно-изотермическим потенциалом, либо энергией Гиббса и обозначили G.
. (55)
Трансформации состояния совокупности в изобарно-изотермическом ходе выражаются через
. (56)
Это значит в совокупности, находящейся при постоянном давлении либо температуре, изобарный потенциал есть мерой энергии, талантливой абсолютно переходить в нужную работу, исходя из этого довольно часто его именуют свободной энергией Гиббса. Вторая же часть полной энергии (TDS) -связанная энергия — не дает работы, а переходит лишь в теплоту, которая безтолку рассеивается в вохдух.
Так как большая часть химических реакций сопровождаются лишь работой расширения, то , тогда:
(57)
Из взятого неравенства видно, какой процесс протекает в совокупности:
- в случае, если (энергия Гиббса убывает, DG имеет отрицательное значение), то в совокупности протекает самопроизвольный процесс;
- в случае, если (энергия Гиббса не изменяется), то совокупность находится в равновесии;
- в случае, если (энергия Гиббса возрастает, DG имеет хорошее значение), то в совокупности протекает несамопроизвольный процесс.
Как показывает опыт, для химических реакций вероятны следующие утверждения:
- в случае, если , реакция вероятна и протекает самопроизвольно не только в стандартных, но и при любых условиях,
- в случае, если
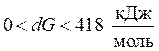возможность осуществить реакцию вызывающа большие сомнения, нужно совершить расчет с целью определения условий, при которых ; - в случае, если
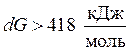, реакция неосуществима в простых условиях, допустимо она будет протекать при необыкновенных температуре и давлении /7/.
Так, изобарно-изотермический потенциал есть критерием, определяющим направленность термодинамического процесса при свободных переменных — температуре и давлении.
Продифференцируем уравнение (55), полагая все параметры состояния (P, V, T) переменными:
.
В случае, если учесть, что , то, подставляя dU и приводя подобные члены, возьмём:
. (58)
Из взятого уравнения находим:
а) при постоянной температуре:
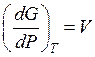. (59)
Вывод: Количество совокупности есть мерой возрастания энергии Гиббса с повышением давления при постоянной температуре;
б) при постоянном давлении
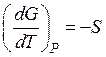. (60)
Вывод: Энтропия есть мерой убыли энергии Гиббса совокупности с повышением температуры при постоянном давлении.