отклонения обычного распределения.Будем искать для среднего квадратического отклонения нормально распределенной случайной величины доверительный промежуток вида (s – ?, s +?), где s – исправленное выборочное среднее квадратическое отклонение, а для ? выполняется условие: p ( |? – s| ? ) = ?.
Запишем это неравенство в виде: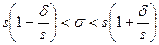 
либо, обозначив 
,
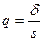. (4)
Разглядим случайную величину ?, определяемую по формуле
,
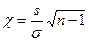которая распределена по закону «хи-квадрат» с п-1 степенями свободы. Плотность ее распределения
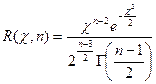
не зависит от оцениваемого параметра ?, а зависит лишь от количества выборки п. Преобразуем неравенство (4) так, дабы оно приняло вид ?1 ? ?2. Возможность исполнения этого неравенства равна доверительной возможности ?, следовательно,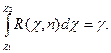 
Предположим, что q 1, тогда неравенство (4) возможно записать так:
,
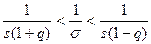либо, по окончании умножения на ,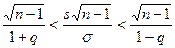 
. Следовательно, 
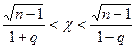. Тогда 
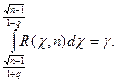Существуют таблицы для распределения «хи-квадрат», из которых возможно отыскать q по заданным п и ?, не решая этого уравнения. Так, вычислив по выборке значение s и выяснив по таблице значение q, возможно отыскать доверительный промежуток (4), в который значение ? попадает с заданной возможностью ?.
Замечание. В случае, если q 1, то с учетом условия ? 0 доверительный промежуток для ? будет иметь границы
. (5)
Итак, для оценки главного среднего квадратического отклонения ? при заданной надежности ? возможно выстроить доверительный промежуток вида
где s – исправленное выборочное среднее квадратическое отклонение, а
q = q (n, ?) – значение, определяемое из таблиц.
Пример.Пускай п = 20, s = 1,3. Отыщем доверительный промежуток для ? при заданной надежности ? = 0,95. Из соответствующей таблицы находим q (n = 20, ? = 0,95 ) = 0,37. Следовательно, границы доверительного промежутка: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 ? 1,781 с возможностью 0,95.
Пример. Дана выборка значений нормально распределенной случайной величины: 2, 3, 3, 4, 2, 5, 5, 5, 6, 3, 6, 3, 4, 4, 4, 6, 5, 7, 3, 5. Отыскать с доверительной возможностью ? = 0,95 границы конфиденциальных промежутков для дисперсии и математического ожидания.
Количество выборки п = 20. Отыщем = 4,25, s = 1,37. По таблицам ([1], табл. 3 и 4) определим t (0,95; 20) = 2,093; q (0,95; 20) = 0,37. Тогда
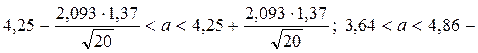
доверительный промежуток для математического ожидания;
доверительный промежуток для дисперсии.
Вопросы для самопроверки
1. В чем сущность задачи по определению параметров главной совокупности? В чем особенности данной задачи?
2. Как вычисляется средняя арифметическая выборки при больших объёмах и малом ее?
3. Как вычисляется дисперсия выборки в случаях большого объёма и малого ее?
4. Какая величина принимается за среднюю главной совокупности, а какая — за дисперсию?
5 Что понимается под доверительной вероятностью и доверительным интервалом?
6. Как вычисляется среднее квадратическое отклонение средней выборки?
7. Назовите выборочные числовые характеристики.
8. Что такое статистики и для чего они помогают?
9. Какими особенностями должны владеть оценки?
10. Какова возможность попадания главной средней в промежуток размером ±2(+3) средних квадратических отклонений средней выборки при обычном распределении.
11. Что именуется доверительной вероятностью и доверительным интервалом?
Дайте неспециализированную схему построения доверительного промежутка.
12. Как изменяется доверительный промежуток с повышением надежности? С повышением количества выборки?
13. Как изменяется доверительный промежуток в зависимости от того, известны ли другие параметры совершенно верно либо нет?
14. В случае, если доверительная возможность будет увеличена, то как изменится доверительный промежуток при вторых равных условиях.
15. Что нужно сделать с количеством выборки, дабы уменьшить доверительный промежуток при том же значении доверительной возможности?
ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ
Расчеты коэффициентов корреляции, регрессии достаточно трудоемки. Это разъясняется тем, что приходится обрабатывать много данных; так как одно наблюдение дает сходу две величины. Но необходимо иметь в виду, что в случае, если количество выборки мал, то расчеты этих коэффициентов несложны. При малых выборках неспециализированную корреляционную таблицу не составляют, а итог наблюдений оставляют в том виде, каким он получается конкретно в опыте, т. е. в виде так называемой несложной корреляционной таблицы. В таковой таблице каждому номеру наблюдений соответствует пара наблюдавшихся значений случайных размеров. Само собой разумеется, вычисленный по малому числу наблюдений коэффициент в целом имеет меньшую надежность. В тех случаях, в то время, когда известен неспециализированный вид зависимости между средней одной величины и значениями второй, параметры данной зависимости смогут быть отысканы способом мельчайших квадратов.
Линейная корреляция
Разглядим выборку двумерной случайной величины (Х, Y) . Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, то есть: условным среднимназовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Подобно условное среднее -среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. Введем уравнения регрессии Y на Х и Х на Y:
M (Y / x) = f (x), M ( X / y ) = ? (y).
Условные средние и являются оценками условных математических ожиданий и, следовательно, также функциями от х и у, другими словами
=f*(x) — (1)
— выборочное уравнение регрессии Y на Х,
= ?*(у) — (2)
— выборочное уравнение регрессии Х на Y.
Соответственно функции f*(x) и ?*(у) именуются выборочной регрессией Y на Х и Х на Y, а их графики – выборочными линиями регрессии. Узнаем, как определять параметры выборочных уравнений регрессии, в случае, если этих уравнений известен.
Пускай изучается двумерная случайная величина (Х, Y), и взята выборка из п пар чисел (х1, у1), (х2, у2),…, (хп, уп). Будем искать параметры прямой линии среднеквадратической регрессии Y на Х вида
Y = ?yxx + b , (3)
Подбирая параметры ?ух и b так, дабы точки на плоскости с координатами (х1, у1), (х2, у2), …, (хп, уп) лежали как возможно ближе к прямой (3). Используем для этого способ мельчайших квадратов и отыщем минимум функции
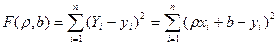. (4)
Приравняем нулю соответствующие частные производные:
.
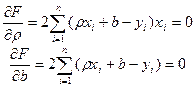В следствии возьмём совокупность двух линейных уравнений довольно ? и b:
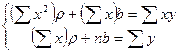. (5)
Ее ответ разрешает отыскать искомые параметры в виде:
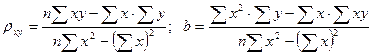. (6)
Наряду с этим предполагалось, что все значения Х и Y наблюдались по одному разу.
Сейчас разглядим случай, в то время, когда имеется большая выборка (не меньше 50 значений), и эти сгруппированы в виде корреляционной таблицы:
| Y | X | ||||
| x1 | x2 | … | xk | ny | |
| y1 y2 … ym | n11 n12 … n1m | n21 n22 … n2m | … … … … | nk1 nk2 … nkm | n11+n21+…+nk1 n12+n22+…+nk2 …………….. n1m+n2m+…+nkm |
| nx | n11+n12+…+n1m | n21+n22+…+n2m | … | nk1+nk2+…+nkm | n=?nx = ?ny |
Тут nij – число появлений в выборке пары чисел (xi, yj). Потому, что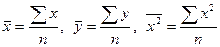 
, заменим в совокупности (5)
, где пху – число появлений пары чисел (х, у). Тогда совокупность (5) примет вид:
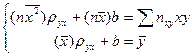. (7)
Возможно решить эту совокупность и отыскать параметры ?ух и b, определяющие выборочное уравнение прямой линии регрессии:
.
Но чаще уравнение регрессии записывают в другом виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения совокупности (7):
.
Подставим это выражение в уравнение регрессии: . Из (7)
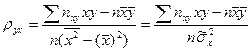, (8)
где Введем понятие выборочного коэффициента корреляции
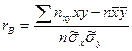
и умножим равенство (8) на :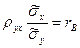 
, откуда 
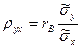. Применяя это соотношение, возьмём выборочное уравнение прямой линии регрессии Y на Х вида
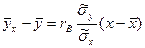. (9)
Коэффициент корреляции – безразмерная величина, которая помогает для оценки степени линейной зависимости между Х и Y: эта сообщение тем посильнее, чем ближе |r| к единице.
Для качественной оценки тесноты корреляционной связи между X и Y возможно воспользоваться таблицей Чеддока (табл.1):
Таблица 1
| Диапазон трансформации | rB | | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Темперамент тесноты связи | не сильный | умеренная | заметная | высокая | довольно высокая |
Итак,в случае, если для выборки двумерной случайной величины (X, Y): {(xi, yi), i = 1, 2,…, n} вычислены выборочные средние и и выборочные средние квадратические отклонения ?х и ?у, то согласно этой информации можно вычислить выборочный коэффициент корреляции
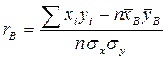
и взять линейные уравнения, обрисовывающие связь между Х и Y, каковые именуются выборочным уравнением прямой линии регрессии Y на Х:
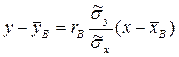
и выборочным уравнением прямой линии регрессии Х на Y :
.
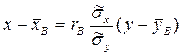Пример. Для выборки двумерной случайной величины
| i | ||||||||||
| xi | 1,2 | 1,5 | 1,8 | 2,1 | 2, 3 | 3,0 | 3,6 | 4,2 | 5,7 | 6,3 |
| yi | 5,6 | 6,8 | 7,8 | 9,4 | 10,3 | 11,4 | 12,9 | 14,8 | 15,2 | 18,5 |
вычислить выборочные средние, выборочные средние квадратические отклонения, выборочный коэффициент корреляции и составить выборочное уравнение прямой линии регрессии Y на Х.
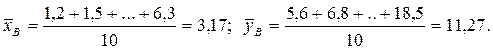
Для определения выборочного коэффициента корреляции вычислим предварительно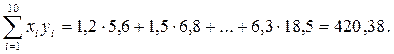 
Тогда
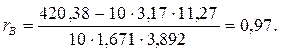Выборочное уравнение прямой линии регрессии Y на Х имеет форму: 
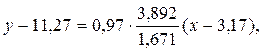либо
Пример. По заданной корреляционной таблице отыскать выборочные средние среднеквадратические отклонения s?, s?, коэффициент корреляции ??? и уравнение линейной регрессии Y на на данный момент. Вычислить условные средние по дан-ным таблицы и отыскать громаднейшее их отклонение от значений, вычисляемых из уравнения регрессии.
| Y X | nX | |||||
| nY |
Вычислим среднеквадратические отклонения и выборочные средние для X,Y
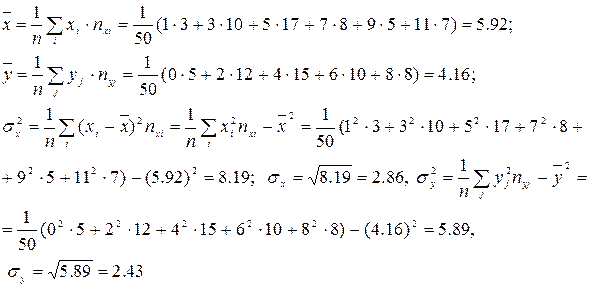
Выборочный коэффициент корреляции между Х и У отыскивается по формуле
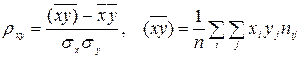
В соответствии с таблице
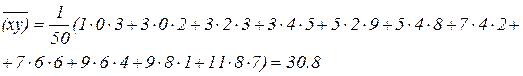
откуда
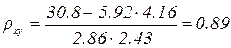
Выборочное линейное уравнение регрессии У на Х имеет форму
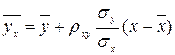
либо, с учётом вычисленных значений,
Условное среднее при x = xi вычисляется по формуле
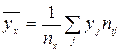
где — число выборочных значений yj , наблюдавшихся при данном xi . По данным из таблицы находим
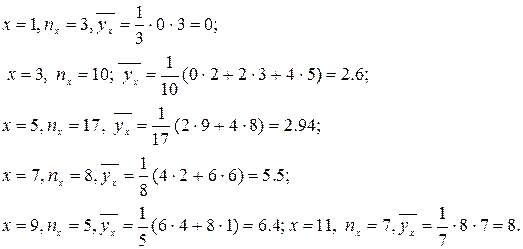
Значения условных средних , отыскиваемые по уравнению регрессии:
Отклонения значений ,
будут d1 = 0-0.45=-0.45; d2 = 2.6- 1.96 = 0.65; d3 = -0.51, d4 = 0.55; d5 = -0.05;
d6 = 0.05. Громаднейшее по безотносительной величине отклонение равняется 0.65.
Пример. Выборочно обследовано 100 снабженческо-сбытовых фирм некоего региона по количеству работников X и количествам складской реализации Y (д.е.). Результаты представлены в корреляционной таблице;
| X У | ny | |||||
| nх | n=100 |
Согласно данным изучения требуется:
1) в прямоугольной совокупности координат выстроить эмпирические ломаные регрессии Y на X и X на Y, сделать предположение в виде корреляционной связи;
2) оценить тесноту линейной корреляционной связи;
3) проверить догадку о значимости выборочного коэффициента корреляции, при уровне значимости ?=0,05;
4) составить линейные уравнения регрессии У на X и X на У, выстроить их графики в одной совокупности координат;
5) применяя полученные уравнения регрессии, оценить ожидаемое среднее значение показателя Y при х=40 чел.; дать экономическую интерпретацию взятых результатов.
1.Для построения эмпирических ломаных регрессии вычислим условные средние и Вычисляем . Так как при х=5 показатель Y имеет распределение
2.
| YY | |||
| ni |
то условное среднее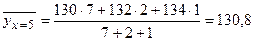 
.
При х=15 показатель Y имеет распределение
| Y | ||||
| ni |
тогда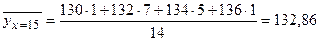 
.
Подобно вычисляются все и .Возьмём таблицы, высказывающие корреляционную зависимость Y от X (табл.2) и X от Y (табл.3).
Таблица 2
| направляться | |||||
| 130,8 | 132,86 | 135,74 | 137,08 | 137,86 |
Таблица 3
| y | ||||||
| 6,25 | 19,54 | 32,35 | 43,57 |
В прямоугольной совокупности координат выстроим точки Аi(хi, ), соединив их отрезками, возьмём эмпирическую линию регрессии Y на X. Подобно строятся точки В j( ,yj) и эмпирическая линия регрессии X на Y (см. рис.).
Выстроенные эмпирические ломаные регрессии Y на X и X на Y говорят о том, что между числом трудящихся (X) и количеством складских реализаций (Y) существует линейная зависимость. Из графика видно, что с повышением X величина кроме этого возрастает, исходя из этого возможно выдвинуть догадку о прямой линейной корреляционной зависимости между числом трудящихся и количеством складских реализаций.
2. Оценим тесноту связи. Вычислим выборочный коэффициент корреляции, предварительно вычислив характеристики по формулам
, 
, 
, 
, 
,
, 
: ;
; ; ;
.
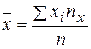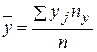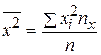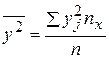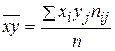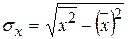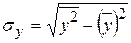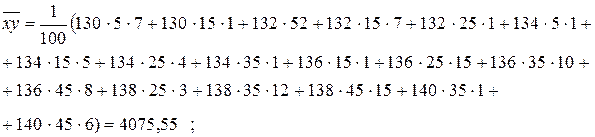
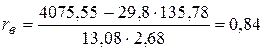Это значение rB показывает, что линейная связь между объёмом и количеством работников складских реализаций высокая. Данный вывод подтверждает начальное предположение, сделанное исходя из графика.
3. Запишем теоретические уравнения линейной регрессии:
, 
.
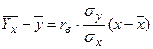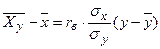Подставляя в эти уравнения отысканные размеры, приобретаем искомые уравнения регрессии:
1) уравнение регрессии Y на X:
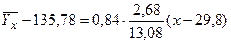, либо ;
2) уравнение регрессии X на Y:
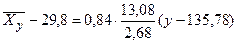, либо .
Выстроим графики отысканных уравнений регрессии. Зададим координаты двух точек, удовлетворяющих уравнению . Пускай х = 10, тогда , А1(10; 132,41), В случае, если х = 40, тогда , А2(40; 137,51). Подобно находим точки, удовлетворяющие уравнению , В1(10,2; 131), В2(43; 139). Графики прямых линий регрессии изображены ниже на рисунке.
Контроль: точка пересечения прямых линий регрессии имеет координаты . В отечественном примере: С(29,8; 135,78).
4. Отыщем среднее значение Y при х=40 чел., применяя уравнение регрессии Y на X. Подставим в это уравнение х=40, возьмём
.
Ожидаемое в главной совокупности среднее значение количества складских реализаций при заданном количестве работников (х=40) образовывает 137,51 д.е.
Замечание 1. В случае, если в корреляционной таблице даны интервальные распределения, то за значения вариант нужно брать середины частичных промежутков.
Замечание 2. В случае, если эти наблюдений над показателями X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:
, 
,
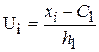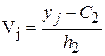где h1 – ход, т.е. разность между двумя соседними вариантами xi; С1 – «фальшивый нуль» вариант xi (в качестве «фальшивого нуля» комфортно принять варианту, которая расположена приблизительно в середине последовательности); h2 – ход вариант Y; С2 – «фальшивый нуль» вариант Y.
В этом случае выборочный коэффициент корреляции
,
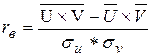где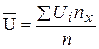 
, 
, 
, 
.
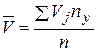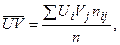
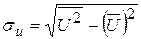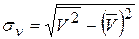Зная эти величины, находят , , ?х, ?у по формулам
, , , .
Отысканные размеры подставляем в уравнения (10).
Так в данном примере С1 =25, h1=10, С2=136, h2=2;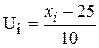 
, 
.
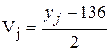Корреляционная таблица в условных вариантах имеет форму
| U V | -2 | -1 | ny | |||
| -3 | ||||||
| -2 | ||||||
| -1 | ||||||
| nx | n=100 |
По данной таблице и приведённым выше формулам находим характеристики:
;
;
;
;
; ;
;
;
;
; .
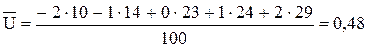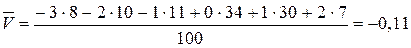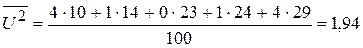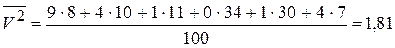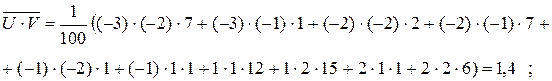
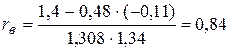В следствии приобретаем те же уравнения линейной регрессии:
; .