Моделирование стационарных процессов.
Понятие стационарности.
Будем осознавать под временным рядом реализацию случайного процесса.
Опр. 1 (строгой стационарности либо стационарности в узком смысле) Случайный процесс есть строго стационарным, в случае, если сдвиг во времени не меняет и одну из функций плотности распределения. Другими словами, в случае, если ко всем моментам времени прибавить некую целочисленную величину, то функция плотности наряду с этим не изменится:
для всех n, моментов времени и целочисленном ?.
Опр. 2 (не сильный стационарности либо стационарности в широком смысле) Случайный процесс именуются стационарным в широком смысле, если он владеет постоянной средней и дисперсией (другими словами математическое ожидание и дисперсия не зависят от времени), а ковариация зависит лишь от временного промежутка между двумя отдельными наблюдениями.
Другими словами случайный процесс vt именуют стационарным, в случае, если для него выполняются следующие условия:
1) М(vt)= М(vt+k)=m=const;
2) D(et)=s2=const;
3) cov(vi,vj)=cov(vi+l,vj+l) при любых i¹j.
Соответственно временные последовательности представленные строго стационарными и слабо стационарными случайными процессами именуются стационарными временными последовательностями в узком и широком смысле.
Авторегрессионные процессы.
Опр. 3. Авторегресонным (Auto-Regressive) именуется процесс, при котором значение последовательности находится в линейной зависимости от прошлых значений.
К примеру, в случае, если текущее замечаемое значение есть функцией всего лишь одного значения, конкретно предшествующего наблюдению, другими словами процесс зависит всего лишь от одного значения разглядываемой переменной, то процесс именуется авторегрссионным процессом первого порядка и обозначается AR(1). Это возможно обобщить следующим образом: в случае, если разбираемый динамический процесс зависит от 1 до n временных лагов назад, то это авторегрессионный процесс порядка n, т. е. AR(n):
(1)
Тут текущее значение Y – функция от n самые недавних прошлых значений.
Уравнение (1) возможно разглядывать как многофакторное уравнение регрессии, где прошлые значения Y являются свободными наблюдениями:
(2)
где – остаток либо неточность (погрешность) .
Модели скользящей средней.
Опр.4. Модель скользящей средней (Moving Average) – это модель, где моделируемая величина задается линейной функцией от прошлых неточностей, т.е. разностей между фактическими наблюдениями и прошлыми.
(3)
где — случайная неточность, m – количество лагов запаздывания.
Термин «скользящая средняя», применяемый тут не следует путать с соответствующим термином, относящимся к непараметрическим способом поиска тренда.
Автокорреляционная и личная автокорреляционная функции.
Для определения степени автокорреляции временных последовательностей нужно найти зависимость между текущими и прошлыми значениями исходного временного последовательности. Это сообщение измеряется посредством коэффициентов автокорреляции, совокупность которых образует автокорреляционную функцию (АКФ, (ACF)).
Опр.5. Коэффициент автокорреляции измеряет связь между текущими и прошлыми наблюдениями временного последовательности и рассчитывается следующим образом:
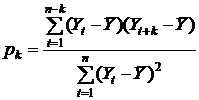 (4)
(4)
где k – количество лагов запаздывания, — среднее значение последовательности.
Так, коэффициент автокорреляции первого порядка будет вычислен с лагом в один период, коэффициент автокорреляции второго порядка будет учитывать степень связи между значениями, отстоящими на два временных периода и т.д. Следовательно, сперва рассчитываются коэффициенты автокорреляции всех порядков, а после этого посредством статистических параметров определяется, при каких лагах коэффициенты значимы (так, определяется порядок авторегрессионного процесса). Личный коэффициент автокорреляции измеряет связь между текущим значением переменной Xt и последующими значениями данной переменной Xt-1, Xt-2, …, Xt-k, в то время, когда влияние всех промежуточных временных лагов устранено. Так, личный коэффициент автокорреляции первого порядка будет равен коэффициенту автокорреляции первого порядка, поскольку нет промежуточных лагов. Но частные коэффициенты второго и следующих порядков будут уже различаться друг от друга.
Опр.6. Личный коэффициент автокорреляции лежит в базе личной автокорреляционной функции (ЧАКФ). Личный коэффициент автокорреляции определяет степень автокорреляции временного последовательности. К примеру, последовательность, обозначенный AR(m), говорит о том, что последний статистически значимый личный коэффициент автокорреляции вычислен с лагом m. (В ряде AR(4) значимыми будут частные коэффициенты автокорреляции с лагами от одного до четырех периодов, но коэффициенты с более высокими лагами не будут значимо различаться от нуля).
В динамическом ходе AR(m) частные коэффициенты автокорреляции значимо отличаются от нуля для временных лагов от 1 до m и после этого быстро падают до нуля для промежутков m+1 и больше.
Опр.7. График автокорреляционной функции, где по оси абсцисс откладывается k – количество лагов запаздывания, а по оси ординат соответствующие значения коэффициентов автокорреляции, именуется коррелограммой АКФ. Подобный график личной автокорреляционной функции именуется личной коррелограммой.