В то время, когда мы оцениваем достаточно однородный участок залежи, то отечественные оценки смогут быть правильными. В случае, если массив неоднородный то точность прогноза будет понижаться, независимо от способа интерполяции. Посредством способа скользящего окна мы можем для каждого участка массива вычислить стандартное отклонение и среднее и взять карту, содержащую эти сведенья. По данной карте мы можем делать выводы, как изменяются отечественные оценки. Существует 4 разновидности трансформаций этих оценок:
1. Местные оценки среднего значения переменной и изменчивости сохраняются в пределах залежи — постоянными.
2. Среднее значение изменяется, имеется тренд, а изменчивость постоянна.
3. Среднее значение неизменно, а изменчивость характеризуется трендом.
4. Среднее изменчивость и значение — непостоянны.
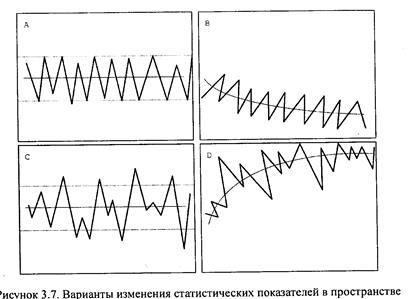
Для оценки параметров первые 2 случая самый предпочтительны, результаты интерполяции получаются более надежными.
На практике довольно часто видятся 3 и 4 случаи, характеризующиеся трансформацией стандартного отклонения переменной, более того видится и ПРОПОРЦИОНАЛЬНЫЙ ЭФФЕКТ. Это возможно заметить на корреляционном графике среднее – стандартное отклонение, но он может провалиться сквозь землю, в случае, если мы постараемся привести отечественное распределение к обычному виду. Пропорциональный эффект отмечается время от времени при логнормальном распределении.
Потому, что поступающая к нам информация собрана по ограниченному количеству наблюдений, то требуется модель, благодаря которой возможно извлечь данные о точках пространства, где не было опробование.
Существует пара дорог построения таких моделей.
Геолого-генетические модели. Это самый перспективный путь развития науки – моделирование процессов, приведших к формированию месторождений. Но процессы, приводящие к формированию рудных залежей весьма сложны для понимания, и тяжело учесть все факторы, каковые приводили к формированию руд, и на данный момент развитие этого направления еще не достигло уровня, нужного для оценки показателей в блоках модели.
Модели поверхностей тренда. Главное предположение, лежащее в базе регрессионных способов, содержится в том, что все сведенья возможно обрисовать полиномами с добавлением компонента случайной неточности. Геологические переменные отображают большое количество мелкомасштабных процессов, каковые накладываются на широкомасштабные процессы, точно обрисовываемые уравнениями тренда. Утверждение о существовании случайной неточности, свидетельствует, что функция имеет довольно много тригонометрических выражений, обрисовывающих повороты и колебания переменной. Главной идеей геостатистики есть, что лучше разбирать корреляции между значениями в точках расположенных на определенных расстояниях друг от друга. Лучший путь представления действительности – это введение случайной компоненты в выражение флуктуации около установленной поверхности, названной Матероном дрифтом, что бы избежать конфликта с термином тренд. Флуктуации не являются неточностями в чистом виде, а скорее компонентами функции с собственной структурой. Матерон ввел понятие пространственная переменная. Допускается, что приращение случайной функции есть слабостационарным, что свидетельствует, что дисперсия и среднее изменяются, но слабо, априорно функция стационарна, другими словами среднее есть константой. Связи между значениями в точках наблюдения возможно разбирать посредством автокорреляции. Мы имеем эти замеров, либо эти опробования в точках наблюдения по какой или выработке либо скважине. Мы можем задаться вопросом – существуют, либо возможно ли распознать какие конкретно или закономерности в этих замерах. Быть может, в этих данных мы можем заметить повторения, в случае, если проводился гамма-каротаж, к примеру осадочных пород и в разрезе уже, было увидено наличие циклотем либо распознать другие закономерности.
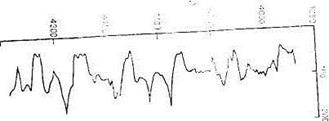
Закономерности возможно установить посредством вычисления меры сходства между участниками данной последовательности, другими словами последовательность сравнивается сама с собой в последовательных положениях и вычисляется степень сходства в перекрывающих промежутках. Это достигается методом смещения последовательности данных довольно самого себя. Расстояние между двумя однообразными точками в смещенной и несмещенной части именуется лагом длины. Лаг длины — это смещение последовательности данных довольно себя самого в предшествующий момент времени. Последовательность данных, возможно, сдвинут довольно себя самого на 1 лаг, 2 лага, 3 лага и без того потом. Минимальная протяженность лага возможно принята равной расстоянию между самый приближенными пробами. В случае, если сравнивать, так, последовательность данных с самим собой, то возможно найти в каких-то положениях хорошее соответствие либо сходство, в других позициях возможно найти громаднейшее несходство. За меру сходства возможно принять автоковариацию, в этом случае автоковариация с лагом 0 не составит большого труда дисперсией.
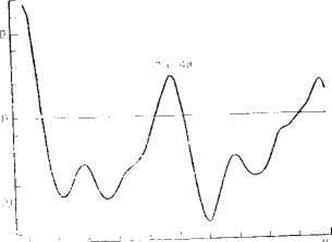
На рисунке изображена автоковариация данных, отображенных на графике.
Имеется соглашение о том, что автоковариация вычисляется для лагов от 0 до приблизительно n\4. Полученный график именуют автоковариограммой либо автоковариационной функцией, которая воображает связь между лага и автоковариации. В случае, если автоковариацию разрешённых стандартизировать то мы возьмём автокорреляцию, а автокорреляционные графики будут именоваться коррелограммами.
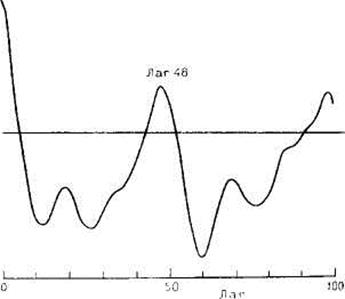
В отличие от прошлой функции она скоро убывает от 1 с нулевым лагом (так как корреляция последовательности с самим собой при лаге равным 0 в любой момент равна 1) до 0 и колеблется около 0.
На графике отражены примеры идеализированных последовательностей данных и их автокорреляционные функции.
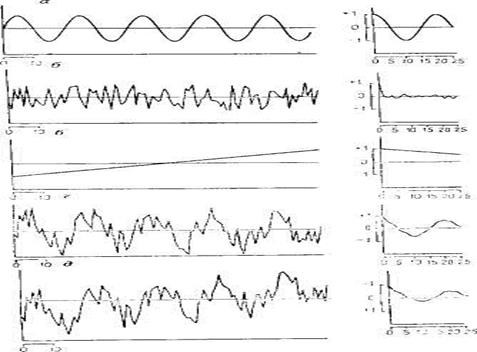
Первая модель отражает синусоидальную волну, вторая модель отражает комплект случайных чисел, третья модель отражает возрастающую по линейному закону последовательность чисел, четвертая воображает синусоидальную волну и наложенный на нее шум, пятая модель воображает синусоидальную волну с наложенным случайным шумом, имеющую линейный тренд.
Основная цель геостатистики пребывает в изучении при оценке трансформаций содержаний компонентов в рудном теле. Главное понятие геостатистики это понятие регионализованной переменной, которая имеет свойства, промежуточные между особенностями случайных размеров и абсолютно детерминированных размеров. В отличие от случайных размеров регионализованные переменные постоянны от точки к точке, но трансформации их так сложны, что они не смогут быть обрисованы какой-либо регулярной детерминированной функцией. Мы знаем лишь значения функции в точках опробования, то есть в пробах, а размер проб, их ориентация, пространственное размещение составляют базу регионализованной переменной, и в случае, если происходят трансформации, хотя бы одного из этих параметров, то и регионализованная переменная будет иметь другие характеристики. Как и каждая вторая теория геостатистика имеет собственную область применения и не имеет возможности употребляться действенно одинаково в любых ситуациях. Дабы действенно применять геостатистику необходимо, дабы была достаточно надежно установлена автокорреляционная сообщение изучаемых компонентов в пространстве и отсутствие в данном пространстве резких трансформаций. Главным инструментом геостатистики есть полувариограмма либо вариограмма, она и употребляется для установления надежной пространственной корреляции между настоящими результатами опробования компонентов. Вариограмма имеется мера степени пространственной зависимости между пробами в заданном направлении, и определяется формулой –
?h=1/2n*?(?i??i+h)2
В случае, если мы вычислим значения для различных h либо вторыми словами лагов, то значения мы можем нанести на график. В то время, когда лаг равен 0, то и значение вариограммы равняется 0. По мере повышения ?h сравниваемые части становятся все менее похожими друг на друга и это ведет к громадным значениям вариограммы, в итоге, значение вариограммы достигнет значения дисперсии, и больше не будет расти и вариограмма перейдет в плоскую область, которая именуется порогом, другими словами пологая часть вариограммы именуется порогом (sill). Расстояние, на котором кривая вариограммы приближается к дисперсии, именуется рангом (range) либо размахом регионализованной переменной, это расстояние определяет окрестность, в пределах которой все значения исследуемого компонента связаны между собой. В российской литературе это расстояние принято именовать территорией влияния.
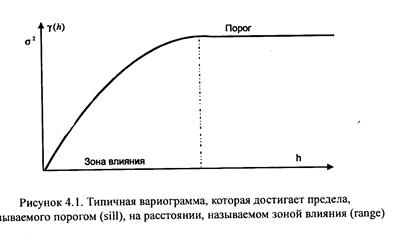
По окончании того как вариограмма достигает ее ограничивающего значения — порога, корреляции между пробами нет. В пределах данной окрестности регионализованная переменная во всех замечаемых точках связана с регионализованной переменной в центральной точке и следовательно возможно использована для оценки ее значения. В случае, если мы используем множество измерений, сделанных в данной области для оценки значения регионализованной переменной в центральной точке, то вариограмма обеспечит личные веса, каковые должны быть приписаны каждому измерению.
Значение вариограммы равняется не только среднему квадрату разности для пар точек расположенных на некоем расстоянии друг от друга, но вариограмма возможно выяснена, как и дисперсия этих разностей,
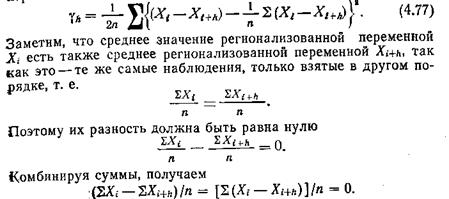
но так как средние ?i и ?i+h равны, то формула уменьшается до
?h=1/2n*?(?i??i+h)2
Как правило вариограмма является точной копией автоковариационной функции и определяется как разность ковариаций и значений дисперсий для данного промежутка расстояний. В случае, если вариограмма еще и стандартизирована и среднее равняется 0, а дисперсия равна 1, то вариограмма делается точной копией автокорреляции.
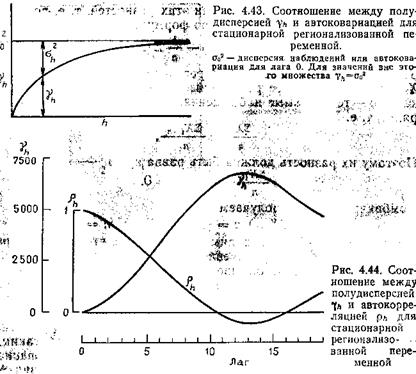
Для стационарных переменных значение вариограммы на расстояние больше территории влияния эквивалентно дисперсии. Не все вариограммы достигают порога, кое-какие из них возрастают с повышением расстояния. Это свойство есть фундаментальным отличием вариограммы от автоковариационной функции, последняя функция существует лишь для стационарных переменных и исходя из этого ограничена.
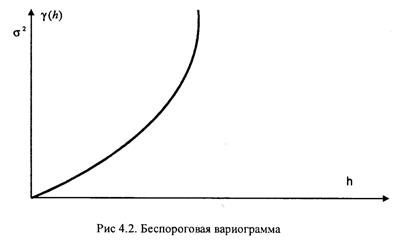
Безпороговая вариограмма говорит о наличии сильного тренда в массиве данных (необходимо каким-то образом убрать тренд).
Примеры расчета вариограмм для одномерного, двухмерного и трехмерного случаев приведены на следующих картинках № .

Рис.№ . Пример расчета вариограммы для одномерного случая.
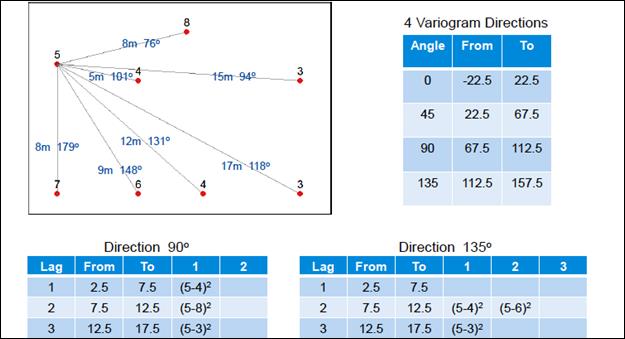
Рис.№ . Пример расчета вариограммы для двухмерного случая.
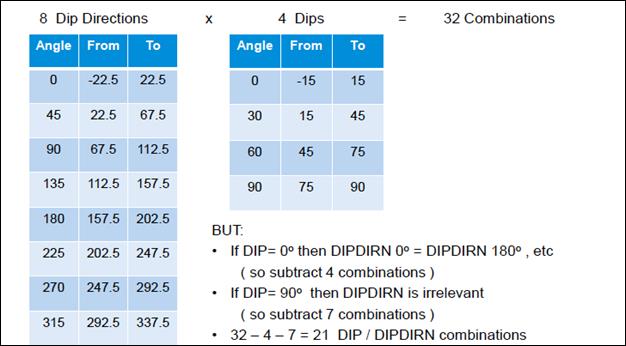
Рис.№ . Пример расчета количества комбинаций при расчете вариограмм в трехмерном пространстве.
Самый принципиально важно изучить поведение вариограммы для малых значений h, поскольку это связано с пространственной регулярностью и непрерывностью исследуемой переменной. На картинках отражены 5 типов поведения вариограммы в начале.
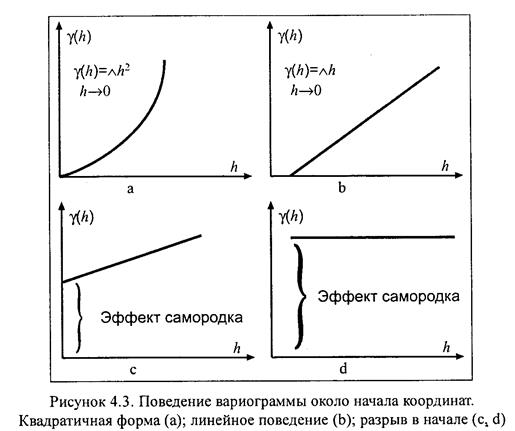
1.Квадратичный. Данный тип говорит о том, что пространственная переменная имеет высокую непрерывность, а функция дифференцируема. Квадратичная форма говорит о присутствии тренда.
2.Линейный. Пространственная переменная постоянна, но не дифференцируема и так менее регулярная (постоянная), чем прошлая.
3.С разрывом в начале. Функция не пытается к нулю, при значениях h родных к нулю. Это указывает, что переменная в высокой степени нерегулярна (не постоянная) на малых расстояниях. Вариограммы большинства геологических переменных имеют, в большинстве случаев, разрыв в начале графика. Это явление именуется эффектом самородков (nugget effect) – это явление в первый раз было отмечено на одном из месторождений Южной Африки, где его связали с присутствием в руде самородков золота. Наличие для того чтобы результата свидетельствует, что содержание компонента может быстро изменяться на родных расстояниях. В большинстве случаев это связано с присутствием в пробах золоторудных месторождений свободного и связанного золота. Связанное золото в минералах изменяется медлено и равномерно распределено в пробах, а свободное золото находится в пробах дискретно. В связи, с этим на родных расстояниях либо в точках опробования близко расположенных друг другу может быстро изменяться значение компонента.
4. Плоский.Чисто случайная функция либо “белый” шум. Пространственные переменные
?i и ?i+h не коррелируются для всех значений h это предельный случай полного отсутствия, какой или структуры. Таковой случай именуют еще чистым эффектом самородков, также такая структура может появиться при громадных расстояниях, между пробами, в то время, когда месторождение разведано редкой сетью опробования. В случае, если вариограмма представляет собой чистый эффект самородков, то использование интерполяции посредством кригинга в этом случае бессмысленно, поскольку между пробами отсутствует корреляционная сообщение, но в полной мере возможно проводить интерполяцию способом обратных расстояний.
5. Обычная.Обычная вариограмма говорит о том, что содержание компонента непрерывно изменяется без каких-либо скачков в зоне влияния. Рисунок данной вариограммы приведен ранее и по сей день.
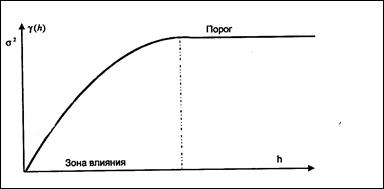
Рис.№ . Обычная вариограмма, она достигает порога (sill), на расстоянии именуемой территорией влияния (range).
не меньше весьма интересно изучение вариограммы, по окончании того как ее значения достигнут порога, часто в данной области возможно заметить так называемый “эффект включений”. Довольно часто он говорит о зональности, другими словами о бедных руд и чередовании богатых. В большинстве случаев данный эффект характеризуется относительной амплитудой, которая определяется отношением большого значения вариограммы (на гребне) к ее порогу. Размер неоднородностей возможно вычислить по графику.
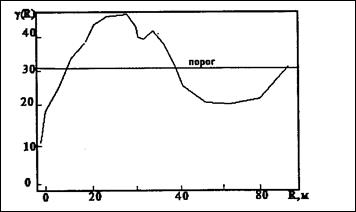
Рис.№ . Эффект включений на вариограмме.
Но самая общая обстоятельство, что эта периодичность возможно связана с статистическими флуктуациями из-за недостаточного количества данных при вычислении вариограммы. Данный эффект еще именуют “скважинным эффектом”.
Положенные структуры.На вариограммах время от времени возможно заметить положенные структуры. На рисунке более долгая территория влияния, разумеется, есть положенной дополнительной структурой, в силу того, что вариограмма достигает порога на этом расстоянии.
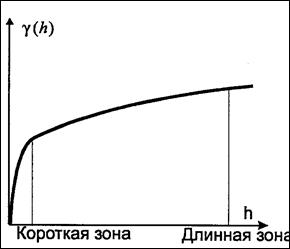
Рис.№ Положенная структура, составленная из структур с маленькой и долгой территориями влияния.
Более маленькую территорию влияния возможно выявить по характерному трансформации кривизны функции. Положенные структуры говорят о процессах, каковые происходили в разных масштабах. Это возможно наличие на месторождении различных типов руд с различными минеральными ассоциациями. Но положенные структуры смогут наблюдаться из-за пропорционального результата – это необходимо контролировать. Самый легкий метод установить имеется ли в массиве данных пропорциональный эффект выстроить график зависимости стандартного отклонения от средних значений для различных горизонтов, участков месторождения.
Присутствие тренда.Теория говорит, что для стационарных переменных вариограмма возрастает медленнее, чем квадрат расстояний для громадных расстояний. На практике довольно часто видится, что вариограмма возрастает стремительнее, чем h2. В этом случае экспериментальная (необработанная либо сырая) вариограмма увеличивает оценку, в отличие от настоящей главной вариограммы.
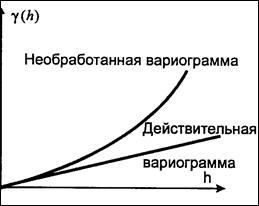
Рис.№ . Вид вариограммы, свидетельствующий о наличии тренда.
Экспериментальная вариограмма равна основной вариограмме плюс параметр смещения в квадрате. В случае, если присутствует тренд, то эмпирическая (экспериментальная) вариограмма переоценивает главную вариограмму. В случае, если наличие тренда установлено, то его авторитет на оценку должно быть устранено.
Один из способов оценки запасов при наличии тренда – это аппроксимация поверхности тренда полиномиальной функцией и расчет отклонений разбираемого показателя массива проб от данной поверхности. По окончании рассчитывается экспериментальная вариограмма для остатков, к ней подбирается пространственная модель, а после этого проводится интерполяция значений остатков методом простого кригинга. На завершающем этапе полученные оценки остатков складываются со значениями поверхности тренда.
Анизотропия.В случае, если вариограмма изменяется от направления, то это говорит о наличие анизотропии на месторождении. Выделяются два типа анизотропии: геометрическую и зональную анизотропию . Геометрическая анизотропия.На рисунке изображены примеры геометрической анизотропии.
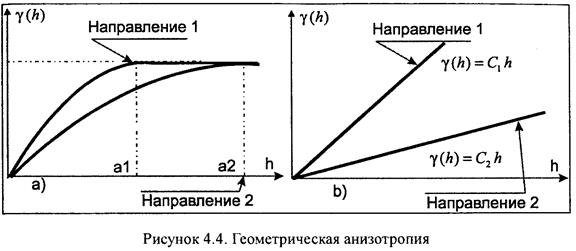
В одном случае вариограммы имеют однообразный порог в обоих направлениях, но территории влияния разны, в другом случае обе функции линейны, но имеют различные углы наклона. В случае, если анизотропию возможно представить в виде эллипса, то такая анизотропия именуется геометрической (аффинная) анизотропией. Что бы убрать геометрическую анизотропию необходимо выяснить коэффициент анизотропии
k=range1/range2 либо k=slope1/slope2
Несложными преобразованиями (применение системы и разворот координат масштабного коэффициента) эллипс преобразовывается в окружность и анизотропия устраняется. В случае, если уравнение вариограммы в направлении 1 обозначить как ?1(h), то конечная вариограмма по окончании исправления будет иметь вид —
?(h)= ?1(vh12+k2 h22)
Но лучше для поиска анизотропии изучить не два направления, а минимум 4 направления как продемонстрировано на рисунке.
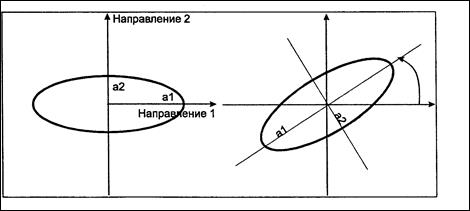
Рис.№ . разворот и Расположение основных осей эллипса при геометрической анизотропии.
В случае, если вычислять анизотропию лишь в двух направлениях, то ее возможно не найти.
Зональная анизотропия.В случае, если мы опробовали зональные стратифицированные руды либо первоначально в выборке находились результаты проб разных способов опробования, к примеру в выборке находились результаты бороздового, задиркового, и валового способов опробования то в этом случае вполне возможно мы можем взять многопороговые вариограммы. Другими словами в различных направлениях вариограммы будут взбираться на пороги различной высоты. В этом случае мы будем иметь зональную анизотропию. Что бы не взять зональную анизотропию необходимо что бы выборка была однородной.
Анализ исходной информации.На первой стадии обработки информации необходимо знать ответы на следующие вопросы: какие конкретно виды опробования употреблялись, какое количество проб было выполнено, какие конкретно типы анализов проводились и в каких лабораториях, были ли трансформации в процедуре опробования на протяжении изучения месторождения, не привлекались ли в различные периоды другие буровые компании, не изменялся ли тип геофизического, каротажного оборудования, есть ли исследуемая геологическая область однородной либо содержит различные типы руд, поделённые во времени либо рудные тела поделены большими тектоническими нарушениями. Потом необходимо решить вопрос, стационарны ли исследуемые переменные, что есть основанием данных, являются ли они аддитивными, с какими разрешёнными работать с самими переменными либо их производными. Геостатистический термин “основание” относится к форме, размеру, количеству единичной пробы. Начальный количество пробы возможно разный при различных видах опробования. Аддитивные переменные это те переменные, каковые распределяются нормально, другими словами среднеарифметическое рудной залежи равняется среднеарифметическому значению всех проб расположенных в данной залежи. Среднеарифметическое содержание дает фальшивую оценку, в случае, если употреблялись пробы различной длины, что бы избежать этого ранее употреблялось преобразование названное аккумуляцией, в то время, когда содержание умножалось на мощность пласта, другими словами определялся “линейный запас”. В большинстве случаев пробы методом композирования приводят к среднему значению длины проб в массиве данных либо к высоте настоящего уступа. Наряду с этим возможно взять в следствии с учетом выделения безрудных прослоев по предполагаемым горным кондициям новые рудные промежутки. В случае, если размеры таких промежутков неодинаковы, то для построения вариограммы и ее анализа возможно применять “линейный запас”, другими словами произведение среднего показателя содержания компонента на этот промежуток на размер промежутка либо мощность залежи. В таких случаях мы приобретаем более надежную вариограмму. Лишь полученные оценки в блоках метропроцента либо метрограмма в элементарных блоках, по окончании интерполяции (по окончании кригинга) необходимо будет поделить на интерполированную оценку мощности рудного тела в данном элементарном блоке. При построении вариограмм необходимо обратить внимание, что размер лага должен быть не более половины расстояния между пробами и допуск лага (расстояние по обе стороны от лага) обязан составлять половину от длины лага, в случае, если размер лага будет больше, то вариограмма будет подниматься выше порога. Количество проб для расчета значения вариограммы не должно быть не больше 23-25. Сперва необходимо строить вариограмму под 90 градусом, а после этого пространство поделить на сектора при вершине 30-60 градусов и весь обьем изучить посредством построения вариограмм в различных направлениях для поиска анизотропии.
Подбор моделей вариограмм.Экспериментальные вариограммы возможно конкретно применять для ответа некоторых геологоразведочных задач. Но ее сложно применять для интерполяции, поскольку значения функции дается лишь в точках вариограммы, для ответа интерполяционных задач нужна информация о значениях вариограммы в произвольных ее точках. Исходя из этого дискретная экспериментальная вариограмма должна быть аппроксимирована постоянной функцией. Опыт подсказывает, что аналитическая форма модели не так ответственна, как ее главные свойства, такие как эффект самородков, наклон линии в начале, территория влияния, порог, анизотропия.
В геостатистике употребляются для аппроксимирования пара функций, сферическая, экспоненциальная, модель Гаусса, каковые взяли громаднейшее распространение и беспороговые модели – линейная и модель Де Вийса (логарифмическая модель). Они отражены на рисунке.
Обычная вариограмма, она достигает порога (sill), на расстоянии именуемой территорией влияния (range).
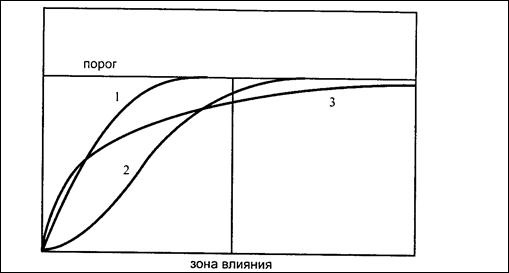
Рис.№ . Пороговые модели вариограмм: 1-сферическая, 2-Гаусса, 3-Экспоненциальная.
Сферической моделью из опыта возможно аппроксимировано более 80% всех вариограмм, эта модель имеет линейное поведение в начале координат и порог в большинстве случаев равный дисперсии. Касательная, совершённая к данной функции от начала координат пересекает линию порога на расстоянии двух территорий влияния, дроблённой на три. Экспоненциальная модель похожа на сферическую модель, она достигает порога на расстоянии трех территорий влияния. Модель Гаусса имеет параболическое поведение в начале координат, редко употребляется на практике. Довольно часто приходится иметь дело с несколькими структурами изменчивости (не более 3), каковые описываются разными моделями. Для каждой структуры подбирается собственная модель, из которых в итоге формируется полная модель исследуемого объекта. Беспороговые модели особенно модель Де Вийса употреблялись ранее заменяя сферическую модель, в то время, когда возможно было без компьтерных вычислений итог.
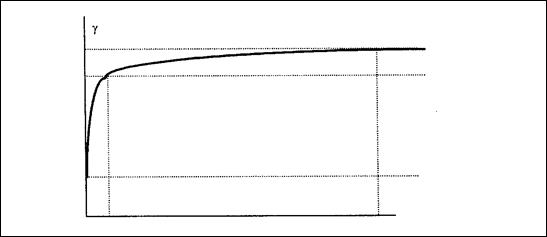
Рис.№ Пример двухструктурной сферической модели вариограммы.
Расчет надежной вариограммы получается лишь из данных подчиняющихся обычному закону распределения, исходя из этого предварительно перед расчетом вариограмм из выборки необходимо убрать все пробы с ураганными значениями и все пробы с минемальными значениями, в этом случае распределение компонента в выборке примет симметричный темперамент. Перед интерполяцией все убранные значения необходимо вернуть в выборку.
Кригинг.Предпосылкой развития геостатистических способов послужило расхождение между содержаниями многих металлов в разведочных пробах и реально извлекаемых количествах руд. Точность оценивания зависит от нескольких факторов, их значений и количества проб, размещения проб по месторождению (тут серьёзна равномерность мест опробования), расстоянием между точкой и пробами в середине оцениваемого блока, наличие пространственной непрерывности разглядываемой переменной (легче оценить величину регулярной переменной, чем той, которая изменяется произвольно). Кригинг – способ интерполяции, что учитывает все эти факторы, был придуман южноафриканским горным инженером Дени Криге и позже усовершенствован Джорджем Матероном. В большинстве способов интерполяции, сперва задается диаметр поискового круга (либо эллипса). Все точки, попавшие в поисковый круг, употребляются для расчета взвешенного среднего, которое будет приписано середине элементарного блока. Веса, с которыми будут учитываться исходные точки, в той либо другой мере, зависят от расстояния от узла до данной точки. Различные способы интерполяции – это различные методы взвешивания данных в зависимости от расстояния. В кригинге, как способе интерполяции, взвешивание производится, пожалуй, сложнее, чем во всех других способах. Допустим, что в отечественный поисковый круг попали пара проб. Расстояния между пробами и расстояния между серединой оцениваемого блока либо его краями употребляется для снятия вариограмных значений с модельной вариограммы. После этого вариограмные значения заносятся в матрицы совокупности линейных уравнений, и рассчитываются коэффициенты уравнений, каковые и являются весами значений компонента в пробах. По окончании рассчитывается оценка элементарного блока блоковой модели рудной залежи. При ответе методом, выбранным Ж. Матероном, появляется маленькое по величине число ? – множитель Лагранжа. Чем множитель меньше, тем лучше решена совокупность линейных уравнений.
Кригинговая оценка рассчитывается по формуле:
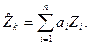
Тут — кригинговая интерполяционная оценка изучаемой переменной, а — значения переменной в n точках, попавших в круг поиска, -веса. В большинстве случаев же, на практике, в поисковый круг попадает пара десятков либо сотен окружающих проб. Соответственно и матричное уравнение расширяется до столбцов и сотен строк.
Считается, что кригинг – это интерполяционная процедура, дающая оценки с мельчайшей дисперсией. Дисперсия кригинга равна
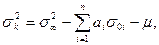
где — порог; — коэффициенты (веса) кригинга; — ковариация между точкой оценивания и i-ой точкой; ? – множитель Лагранжа.
Чем меньше дисперсия кригинга если сравнивать с неспециализированной дисперсией, тем лучше уровень качества взятой оценки.
Точечный либо ординарный кригинг рассчитывается для 8 точек, простой кригинг для одной точки.
Сейчас показались работы (Кумбс), в которых исследуется, как возможно посредством вариограммы оценить степень достоверности ресурсов. Выводы о связи размеров территории влияния с степенью достоверности оценки компонента в элементарном блоке блочной модели напрямую связаны с тем, что вариограмма есть обратной автокорреляционной функцией, исходя из этого оценка посредством значений проб, находящихся на близком расстоянии самый точна в связи с тем что в данной территории влияния значения проб имеют между собой высокую корреляцию. В работе Кумбс предложен следующий механизм оценки степени достоверности. В случае, если значение в блоке интерполировано посредством значений проб, расположенных в части территории влияния, ограниченной 2/3 расстояния от 0 до порога (sill), то степень достоверности этого блока возможно выяснить по категории оцененных ресурсов (measured). В случае, если значение в блоке интерполировано посредством проб, расположенных между первой частью территории влияния и самой территорией влияния, то степень достоверности этого блока возможно выяснить по категории распознанных ресурсов (indicated). И в случае, если значение в блоке интерполировано посредством проб, находящихся за территорией влияния, то степень достоверности этого блока возможно выяснить по категории предполагаемых (прогнозных) ресурсов (inferred). Применение вариограммы для оценки степени достоверности ресурсов в блоковых моделях приведено на рис.№ .
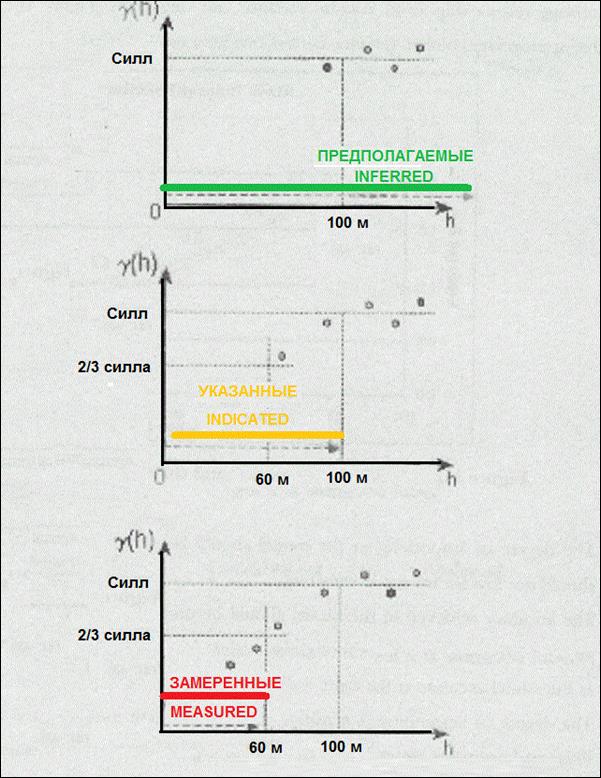
Рис.№ . Применение вариограмм в качестве указателя при классификации ресурсов/запасов.