Алгоритмические операторы matlab

Кроме программ с линейной структурой, инструкции которых исполняются строго по порядку, существует множество методов, структура которых нелинейная. Наряду с этим последовательность элементов методов может выполняться в зависимости от определенных условий, время от времени с конечным числом повторений – регулярных циклов, время от времени в виде циклов, завершаемых при исполнении заданного условия. Фактически каждая важная программа имеет нелинейную структуру. Для таких программ нужны особые управляющие структуры. Они имеются в любом языке программирования большого уровня, и в частности в Matlab.

Разглядим операторы m-файлов подробнее.

Оператор присваивания. Главным оператором совокупности программирования MatLab есть оператор присваивания, имеющий следующую структуру:

ИмяПеременной=выражение

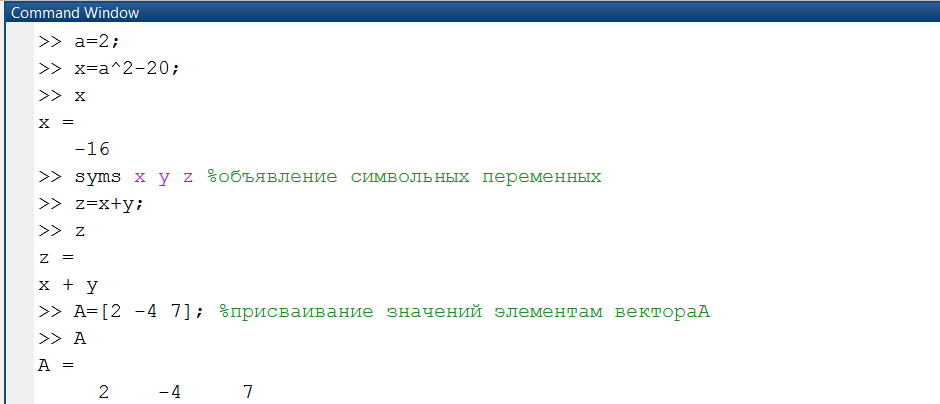
Оператор рекомендован для идентификации переменных и обозначается знаком =, слева от которого находится имя переменной, а справа арифметическое либо строковое выражение (правила записи арифметических и строковых выражений были рассмотрены в п. 1.1.2). Приведем пара примеров операторов присваивания (рис. 1.3.4-1).

Рис. 1.3.4-1. Примеры операторов присваивания

Все переменные, применяемые в правой части оператора присваивания, должны быть предварительно выяснены. В случае, если командная строчок заканчивается знаком точка с запятой (;), то итог исполнения оператора не выводится, в противном случае он выводится в следующей строчке командного окна. Это замечание распространяется и на исполнение операторов присваивания, расположенных в m-файлах.

Операторы ввода данных. Ввод данных в Matlab может осуществляться как с применением оператора присваивания (a=5;), так и с применением функции ввода данных с клавиатуры:

ИмяПеременной= input (‘Запроc’);

Эта функция вводит выражение с клавиатуры, а итог заносится в переменную с именем a. В приведенном ниже примере в переменную a введено сначала числовое значение, а после этого числовое выражение (рис. 1.3.4-2).

Рис. 1.3.4-2. Ввод данных с клавиатуры

Функция input()может употребляться и для ввода произвольных строковых выражений. Наряду с этим она задается в следующем виде:

input(‘Запроc’, V);

При исполнении данной функции вычисления останавливаются в ожидании ввода строкового выражения. Введенное выражение выводится в следующей строчке. Для вычисления выражения, заданного в символьном виде, использована функция eval(). Это иллюстрирует пример на рис. 1.3.4-3.

Рис. 1.3.4-3. Вычисление выражения, заданного в символьном виде

Условный оператор if…end. Условный оператор ifв неспециализированном виде записывается следующим образом:

ifЛогическоеВыражение1

Инструкции1

elselfУсловие2

ЛогическоеВыражение2

Else

ЛогическоеВыражение3

End

Правила записи логических выражений обрисовано в Теме 1.1.

Эта конструкция допускает пара частных вариантов. Простейшее – усеченное разветвление [x] имеет следующий вид:

ifЛогическоеВыражение

Инструкции

End

Отметим, что в случае, если ЛогическоеВыражение возвращает логическое значение 1 (другими словами «Истина»), выполняются Инструкции, составляющие тело структуры if…end. Наряду с этим оператор end говорит о конце списка руководств. Инструкции в перечне разделяют запятая либо точка с запятой. В случае, если ЛогическоеВыражение не выполняется (дает логическое значение 0, «Неправда»), то Инструкции кроме этого не выполняются.

Ниже приведен пример применения несложного усеченного разветвления, реализованного с применения оператора if (рис. 1.3.4-4).

Рис. 1.3.4-4. Пример усеченного разветвления

Вторая личная конструкция напоминает стандартное разветвление [x]:

ifЛогическоеВыражение

Инструкции1

Else

Инструкции2

End

Тут выполняются Инструкции1, в случае, если выполняется действительно
ЛогическоеВыражение, либо, в другом случае, выполняются
Инструкции2.

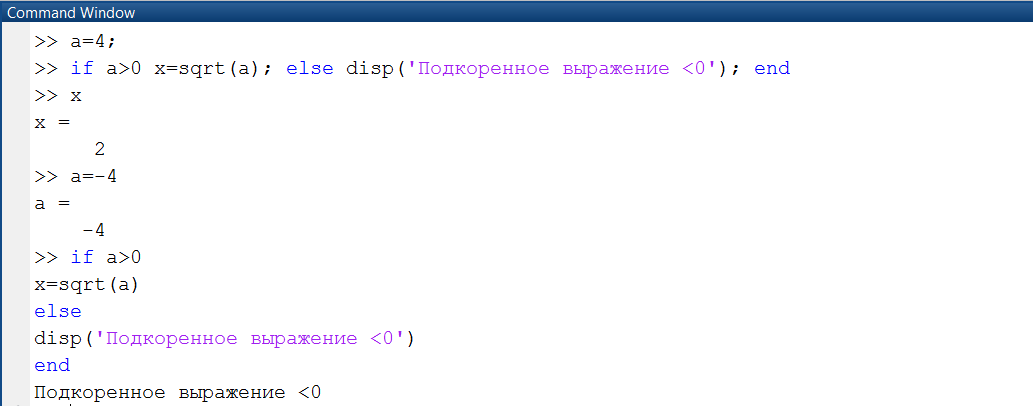
В примере, приведенном на рис. 1.3.4-5, рассматривается стандартное разветвление, реализованное с применением оператора if.

Рис. 1.3.4-5. Пример стандартного разветвления

Из приведенного примера видно, что оператор ifможет быть как в одну строчок, так и в пара строчков.

Разглядим пример более сложного — положенного разветвления. Разглядим пример

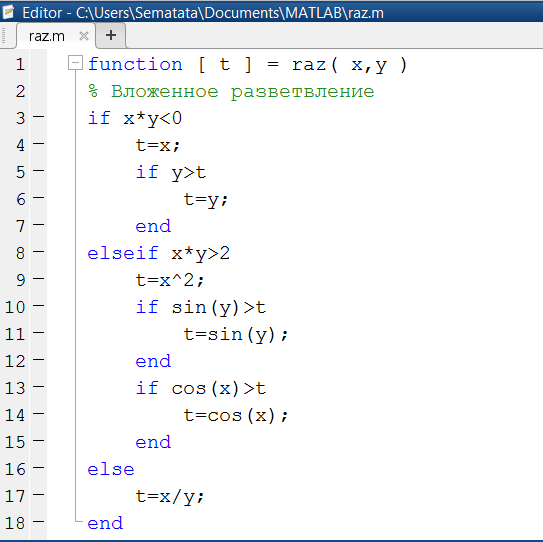
причем, чтобы абсолютно отразить структуру сложного разветвления, не заботясь о переносе долгих командных строчков, используем m-функцию (рис. 1.3.4-7). Подберем эти для проверки главного разветвления и обратимся к функции raz() с разными исходными данными (рис. 1.3.4-6).

Рис. 1.3.4-6. Обращение к функции raz()с разными исходными данными

Рис. 1.3.4-7. Функция, реализующая положенное разветвление

Оператор множественного выбора – switch. Для осуществления множественного выбора употребляется следующая конструкция switch:

switchBыражение

caseЗачение_1

Список_инструкций_1

caseЗначение_2

Список_инструкций_2

…

caseЗначение_N

Список_инструкций_N

Otherwise

Список_инструкций_N+1

End

В случае, если выражение по окончании заголовка switch имеет значение одного из выражений Значение…, то выполняется блок операторов case, в другом случае — перечень руководств по окончании оператора otherwise. При исполнении блока case исполняются те перечни руководств, для которых Значение сходится с Bыpaжением. Обратите внимание на то, что Значение возможно числом, константой, переменной, вектором ячеек либо кроме того строчной переменной. Поясним применения оператора перебора switchследующим примером:

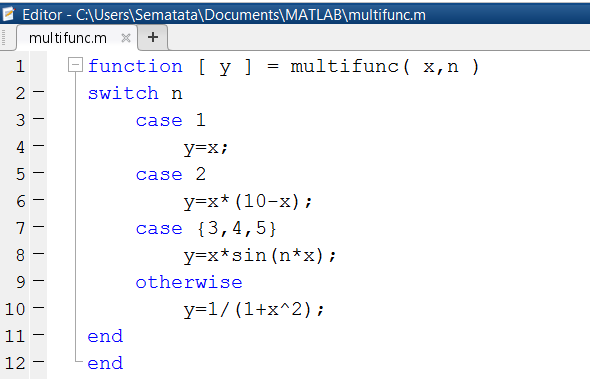
M-функция, реализующая множественное разветвление, приведена на рис. 1.3.4-8, а обращение к ней при данных, разрешающих проверить каждую ветвь разветвления, продемонстрировано на рис. 1.3.4-9.

Рис. 1.3.4-8. Функция, реализующая множественное разветвление

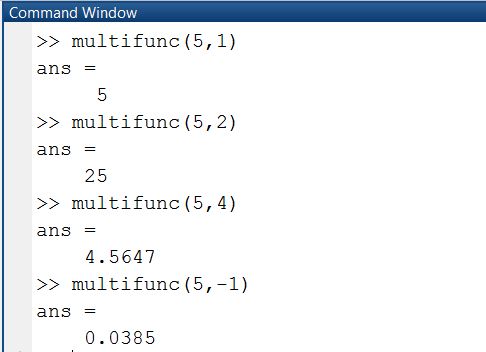
Рис. 1.3.4-9. Обращения к функции multifunc()

У функции multifunc(x,n) два параметра, причем второй играет роль индикатора, определяющего тип функциональной зависимости. Значение функции записывается в переменную y. В случае, если n=1, то выполняется первый case-блок, в случае, если 2, то – второй, в случае, если n=2, 3 либо 4, то – третий. В случае, если же значение переменной n не сходится ни с одним из перечисленных значений, то выполняется команда, расположенная по окончании главного слова otherwise.

Оператор регулярного цикла – for…end. Оператор цикла типа for…end в большинстве случаев употребляется для организации вычислений с заданным числом повторений циклов. Конструкция для того чтобы цикла имеет следующий вид:

for vаг = s:d:e

Инструкция1

….

ИнструкцияN

End

где s — начальное значение переменной цикла var, d — приращение данной переменной и е — конечное значение управляющей переменной, при превышении которого цикл завершается. Вероятна и запись в виде s:е (в этом случае d=l). Перечень делаемых в цикле руководств завершается оператором end.

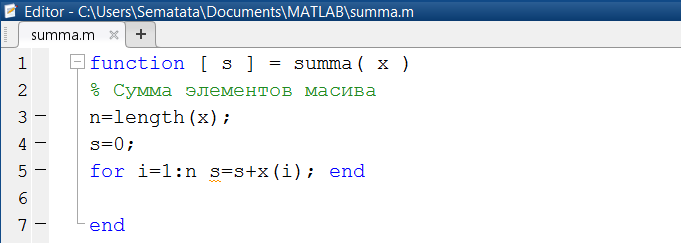
Как пример применения оператора for…end вычислим сумму элементов массива х, значения которого выяснены в командном окне с применением m-функции summa()(рис. 1.3.4-10), параметром которой помогает вектор x. Количество элементов массива х определяется функцией length. Не считая обращения к функции в командном окне предусмотрена проверка результата вычислений с применением встроенной функции sum(x) (рис. 1.3.4-11).

Рис. 1.3.4-10. Функция, вычисляющая сумму элементов массива

Рис. 1.3.4-11. Обращение к функции summa() и встроенной функции sum()

В цикле возможно использован оператор continue, что передает управление в следующую итерацию цикла, пропуская операторы, каковые записаны за ним, причем во положенном цикле он передает управление на следующую итерацию главного цикла. Оператор break может употребляться для досрочного прерывания исполнения цикла (к примеру, при отладке участка программы). Когда он видится в программе, цикл прерывается.

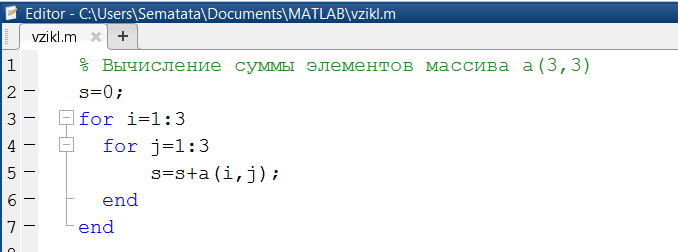
Не считая несложных регулярных циклов в Matlab имеется возможность организации положенных циклов. Разглядим пример формирования двумерного массива а, любой элемент которого воображает сумму его индексов (рис. 1.3.4-12). Обращение к script-файлу vzikl приведено на рис. 1.3.4-13.

Рис. 1.3.4-12. Script-файл, иллюстрирующий положенные циклы

Рис. 1.3.4-13. Обращение к script-файлу с именем vzikl

Оператор итеративного цикла – while…end. Неспециализированный вид структуры while…end выглядит следующим образом:

whileЛогическоеВыражение

Инструкции

End

Отличительной изюминкой данной структуры есть то, что инструкции, расположенные в теле структуры повторения, выполняются лишь в том случае, если некое ЛогическоеВыражение «действительно». Когда условие делается «фальшивым», происходит выход из структуры повторения, и управление передается на инструкцию, расположенную по окончании главного слова end.

Приведем несложной пример (рис. 1.3.4-14).

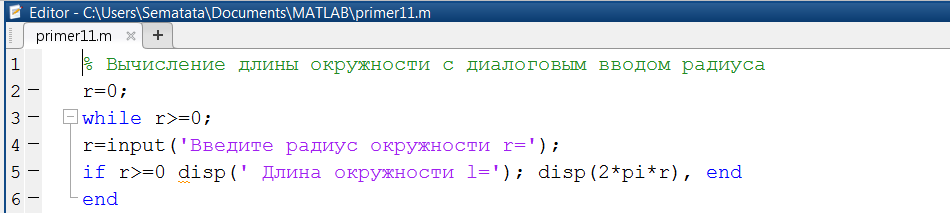
Рис. 1.3.4-14. Диалоговая программа, применяющая оператор while…end

Эта программа, сохраненная в m-файле с именем primer11, помогает для многократного вычисления длины окружности по вводимому пользователем значению радиуса r, где диалог реализован посредством команды input.Cтроки, которые связаны с вводом переменной r и вычислением длины окружности, включены в управляющую структуру while…end. Это нужно для циклического повторения вычислений при вводе разных значений r. До тех пор пока r=0, цикл повторяется. Но стоит задать r

Работа с программой в командном окне представлена на рис. 1.3.4-15.

Рис. 1.3.4-15. Обращения к программе вычисления длины окружности

В управляющих структурах, в частности в циклах forи while, довольно часто употребляются операторы, воздействующие на их исполнение. Так, оператор break может употребляться для досрочного прерывания исполнения цикла. Когда он видится в программе, цикл прерывается.

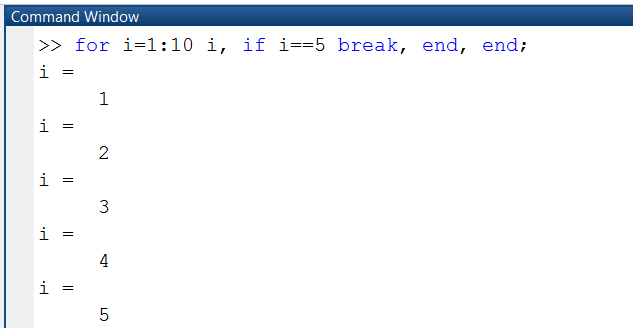
Разглядим пример досрочного прерывания цикла при исполнении условия i=5 (рис. 1.3.4-16).

Рис. 1.3.4-16. Прерывание программы с применением оператора break

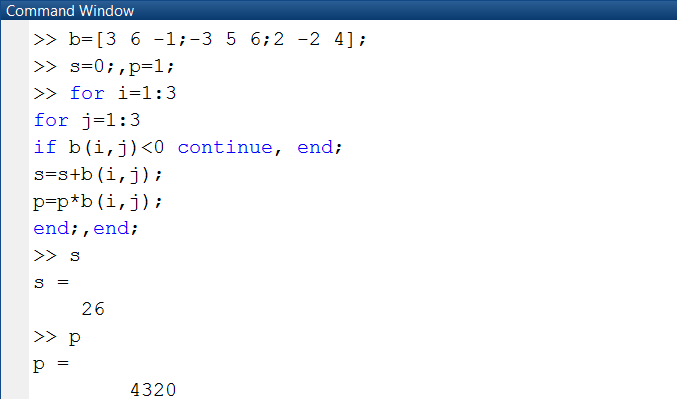
Оператор continue передает управление в следующую итерацию цикла, пропуская операторы, каковые записаны за ним, причем во положенном цикле он передает управление на следующую итерацию главного цикла. Ниже приведен произведения вычисления и пример суммы хороших элементов двумерного массива b(3,3) (рис. 1.3.4-17).

Рис. 1.3.4-17. Прерывание программы с применением оператора continue

Примеры ответа задач с применением

M-файлов

Пример 1.3.5-1. Даны n чисел 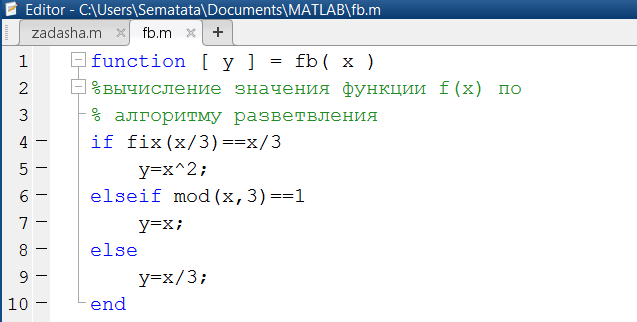. Требуется вычислить их сумму: где

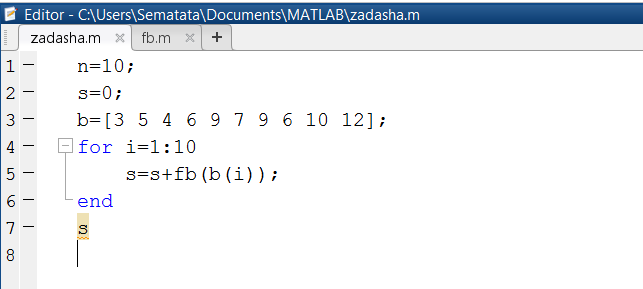
Для решения поставленной задачи создана функция fb(x), реализующая метод вычисления текущего значения функции. Функция имеет один входной параметр – текущее значение элемента массива b и один выходной параметр – y(рис. 1.3.5-1). Обращение к функции происходит в цикле, организованном для вычисления суммы (рис. 1.3.5-2).

Рис. 1.3.5-1. Функция, реализующая метод Примера 1.3.5-1

Рис. 1.3.5-2. Программа, реализующая вычисление суммы чисел

Для вычисления суммы значений функции создан script-файл с именем zadashа.m, в котором сперва заданы количество чисел (n=10) и вектор их значений (b), а после этого организован регулярный цикл для обращения в функции fb() и вычисления суммы.

Вычисления производятся запуском script-файла методом комплекта в командной строчке окна Command Window его имени zadasha. Результаты его исполнения выведены на рис. 1.3.5-3.

Рис. 1.3.5-3. Запуск script-файла zadasha на исполнение

Пример 1.3.5-2. Организовать из произвольных чисел двумерный массив а(3,4). Вычислить и вывести одномерный массив b, любой элемент которого имеется среднее арифметическое элементов соответствующей строки массива а[].

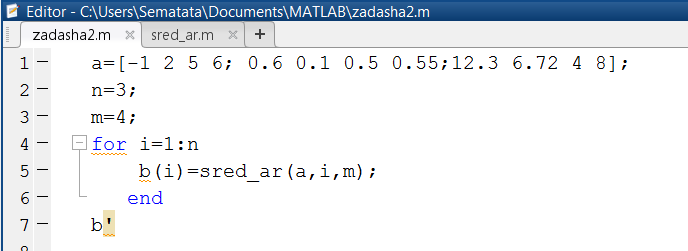
На рис. 1.3.5-4 приведен script-файл с именем направляться2, где введена матрица, а, складывающаяся из трех строчков и четырех столбцов. Организован цикл по количеству формируемых элементов массива b методом обращения к функции sred_ar(). В функцию передается массив а, номер строчка (i) и количество элементов в строчке (m). Вывод элементов массива b предусмотрен в столбец.

Рис. 1.3.5-4. Программа формирования массива b

Функция sred_ar() (рис. 1.3.5-5) предназначена для создания i-го элемента массива b, равного среднему арифметическому элементов строчка массива а.

Рис. 1.3.5-5. Функция sred_ar(), вычисляющая среднее арифметическое
элементов строчка массива a

В следствии запуска script-файле с именем zadasha2в окно Command Windowвыводится столбец элементов массива b

Рис. 1.3.5-6. Запуск script-файла zadasha2

Пример. 1.3.5-3. Задать настоящие числа a,b, натуральное n (a , где , в случае, если

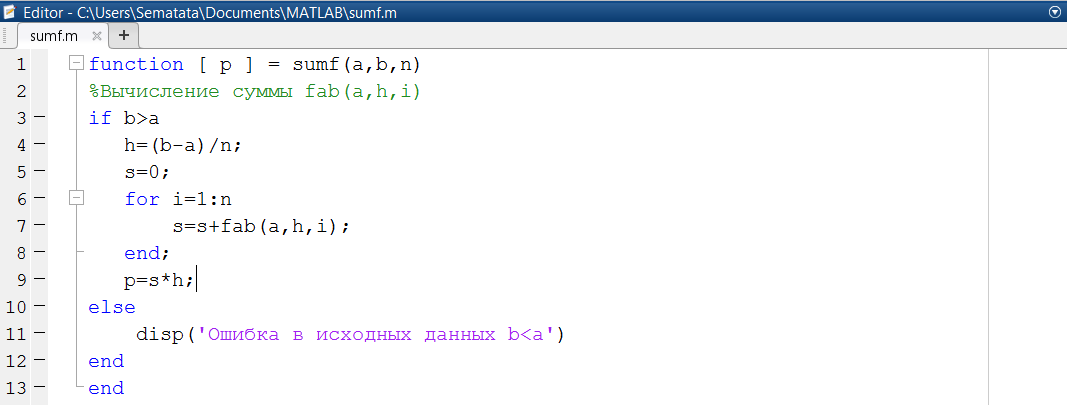
Ответ задачи требует разработки двух функций: fab(a, h, i), предназначенной для вычисления i-го слагаемого (рис. 1.3.5-7) и sumf(a, h, n), предназначенной для вычисления заданного выражения (рис. 1.3.5-8).

Рис. 1.3.5-7. Функция fab(), вычисляющая значение i-го слагаемого

Рис. 1.3.5-8. Функция sumf(), вычисляющая заданное выражение

Запуск на исполнение осуществляется из командного окна к функции sumf(). Предварительно переменным a,b и n присваиваются числовые значения. Проверка правильности ввода данных предусмотрена в функции sumf(). Вычисления выполняются, и итог выводится на экран лишь , если ba, в противном случае в командной строчке появляется сообщение «Неточность в данных b

Рис. 1.3.5-9. Запуск функции sumf() на исполнение

Лабораторная работа по теме

«программирования и Средства алгоритмизации

В Matlab»

Вопросы, подлежащие изучению

1) Виды m-файлов.

2) сохранение и Создание новых, и открытие ранее созданных m-файлов.

3) Особенности script-файлов и m-функций.

4) Запуск на исполнение script-файла из текстового процессора.

5) Запуск на исполнение script-файла из командного окна.

6) Обращения к script-файлам и m-функциям.

7) Средства языка программирования в совокупности Matlab.

Главные операторы m-языка их форматы и назначение.

2. Неспециализированное задание

1) Изучите материал Темы 1.3 (п.п. 1.3.1 – 1.3.5).

2) Выберите личное задание из табл. 1.3.6-1.

3) Создайте m-функции для реализации стандартных методов: вычисления конечных сумм, разветвлений, максимума и поиска минимума в последовательности данных и т.п.

4) Введите и сохранитеm-функции на внешнем носителе.

5) Создайте новый script-файл, в который введите код программы, обрисовывающий логику ответа поставленной задачи.

6) Сохраните script-файл в текущем каталоге.

7) Сделайте отладку script-файла, запуская его на исполнение из текстового процессора командой Run.

Подготовьте и введите данные для ответа поставленной задачи;

9) Выполните script-файл из командной строчка окна Command Window.

10) Сохраните текст рабочего окна на внешнем носителе.

11) Предоставьте результаты работы учителю, ответьте на поставленные вопросы.

12) Выполните команду clear all для очистки Рабочей среды.

13) Оформите отчет по выполненной работе.

Варианты личных заданий

Таблица 1.3.6-1

№	Задание
	Ввести натуральное число nи вектор настоящих чисел Отыскать: где
	Вычислить где
	Задать массив , складывающийся из четного количества элементов. Любая пара чисел , где i+1 кратно двум, задает координаты вершины ломаной. Выстроить ломаную, соединив наряду с этим последнюю вершину с первой
	Ввести натуральное число n и вектор настоящих чисел . Вычислить произведение , где
	Ввести натуральное число n и настоящее число х. Вычислить
	Ввести натуральное число n. Отыскать громаднейшее среди значений , где k=1, 2,…,n, и сумму всех взятых значений
	Ввести натуральное число n. Среди значений , где (i=1,2,…n), отыскать все хорошие и вычислить их сумму
	Ввести натуральное число n и вектор настоящих чисел . Выяснить, хороших либо отрицательных чисел в векторе больше, и выяснить громаднейшее из отрицательных и мельчайшее из положительных чисел
	Ввести матрицу B(5,7) и организовать из первых громаднейших элементов строчков вектор С(5). Вывести его элементы в столбец и строку
	Организовать вектор по правилу: , где k=2,3,…, 7, в случае, если Отыскать сумму квадратов тех чисел, каковые не превосходят 2
	Ввести натуральное число n и вектор настоящих чисел . Отыскать количество двух соседних положительных чисел и двух соседних чисел различного символа
	Ввести квадратную матрицу А(4,4). Организовать из больших элементов ее столбцов вектор X, вывести его элементы на экран в обратной последовательности и прямой
	Ввести вектор целых чисел . Преобразовать его так, дабы сперва размешались нули, после этого все остальные элементы. Выяснить количество и сумму элементов, значения которых кратно 5
	Ввести вектор вещественных чисел . Создать из него массив x, любой элемент которого большой из трех элементов, идущих подряд в массиве z
	Организовать матрицу А(4,4) по правилу: Отыскать и вывести значения и индексы двух однообразных элементов. В случае, если таковых не окажется, вывести сообщение
	Организовать матрицу D(3,2) по правилу: . Создать вектор из отрицательных элементов взятой матрицы
	Задать натуральное число n. Посчитать, какая из матриц размером nна n содержит больше хороших элементов, в случае, если их элементы формируются по правилу: Вывести на экран организованные матрицы
	Ввести квадратную матрицу вещественных чисел А(4,4). Отыскать сумму громаднейших значений элементов ее строчков. Организовать новую матрицу В(4,4) методом умножения каждого элемента матрицы А на отысканную сумму и делением его на определитель исходной матрицы
	Ввести матрицу вещественных чисел А(4,7) и взять из нее вектор С(4), элементы которого это: · громаднейший из элементов в первой строке; · мельчайший из элементов во второй строке; · среднее арифметическое элементов третьей строки; · сумма элементов четвертой строки
	Ввести натуральное число n и матрицу вещественных чисел С(n,n). Отыскать среднее арифметическое громаднейшего и мельчайшего значений ее элементов и, заменив этим значением диагональные элементы, вывести матрицу С на экран
	Ввести натуральные числа k1, k2 и настоящую матрицу размера 8х4. Поменять в матрице местами элементы k1 и k2 строчков
	Ввести натуральное число n и матрицу вещественных чисел С(n,9). Отыскать среднее арифметического каждого из столбцов, имеющих четные номера
	Ввести векторы настоящих чисел x(5), y(6),z(7). Вычислить величину t по следующему методу:
	Ввести векторы настоящих чисел x(5). Взять для х=1, 3, 4 значения где
	Ввести векторы настоящих чисел x(10). Взять из него второй массив p(10), элементы которого упорядочены по возрастанию
	Ввести матрицу вещественных чисел А(3,4). Заменить элементы строчка матрицы с большой суммой значений элементов – единицами, с минимальной — двойками, а остальные элементы матрицы положить равными нулю
	Организовать матрицу А(4,4) по правилу Удалить из него столбцы, которые содержат элементы, меньшие 10
	Организовать матрицу В(9,3) по правилу Выяснить мельчайший элемент в каждой строке матрицы и записать его в соответствующий элемент вектора С. Вывести полученный вектор С
	Ввести матрицу вещественных чисел А(3,4), все элементы которой разны. В каждой строке направляться выбрать громаднейшее и мельчайшее значения, а сумму индексов столбцов, в которых они расположены, записать в соответствующий элемент вектора С(3)
	Ввести матрицу вещественных чисел А(4,4). Взять последовательности элементов основной и побочной диагонали, создать из этих элементов векторы B(4) и C(4) и вывести их на экран

Содержание отчета

1) В форме комментариев:

• Наименование лабораторной работы
• ФИО студента, номер группы
• № варианта
• Личное задание

2) Протокол вычислений (сессии) в окне Command Window, снабженный нужными комментариями.

1.3.7. Контрольные вопросы по теме

1) Что такое script-файл и каковы его особенности?

2) Как именно script-файл запускается на исполнение?

3) Что такое m-функция?

4) В чем отличие script-файла от m-функции?

5) Может ли m-функция иметь пара выходных параметров?

6) Обращение к m-функции.

7) Формат оператора input().

Как с применением оператора if…end реализовать стандартное, усеченное и положенное разветвление?

9) Формат оператора множественного разветвления switch.

10) Формат оператора регулярного цикла for…end, особенности задания значений переменной цикла.

11) Назначение операторов continue и brek.

12) Оператор итеративного цикла while…end и его структура.

1.

Раздел 2. Разработка ответа
вычислительных задач средствами MatLab

Построение графиков функции одной переменной. Работа с массивами / Matlab

Интересные записи:

• А к у с т о э л е к т р о н и к а
• Алу и назначение регистров процессора.
• Анализа воспитательного занятия
• Анализ эмоции «недовольство»