Пускай и – два линейных преобразования линейного пространства L.
Определение 6
Суммой преобразований и именуется преобразование C такое, что хILCх = х + х. Обозначают сумму преобразований C = + .
К примеру, в случае, если :R2®R2 такое, что х = [х1, х2]IR2 х = [х1+х2, 2х2], а :R2®R2 такое, что х = [х1, х2] х = [3х1, х1 –2х2], то преобразование C = + такое, что х = [х1, х2]IR2
C х = х + х = [х1+х2, 2х2] + [3х1, х1 –2х2] = [4х1+х2, х1].
Пользуясь определением 6, возможно доказать, что сумма линейных преобразований имеется линейное преобразование:
C (х + у) = (х + у) + (х + у) = х + у + х + у =
= ( + )х + ( + )у = C х +C у,
C (aх) = (aх) + (кожный покров) = a( х) +a( D) = a( х + х) = aC х.
Отыщем матрицу С преобразования C = + .
Пускай линейного пространства и преобразования L в некоем базисе Б имеют соответственно матрицы А и В. Разглядим произвольный вектор хIL. Обозначим:
Х – координатный столбец вектора х в базисе Б;
– координатный столбец образа уA= х вектора х при преобразовании в базисе Б;
– координатный столбец образа уB = х вектора х при преобразовании в базисе Б;
– координатный столбец образа уC= Cх вектора х при преобразовании C в базисе Б.
Тогда = АХ, = ВХ, = СХ.
Но, в соответствии с определению преобразования C = + , имеем:
C х = ( + )х = х + х,
либо, в матричной форме
= + = АХ + ВХ = (А + В)Х,
Взяли = СХ и = (А + В)Х, откуда С = А + В. Так, матрица суммы преобразований равна сумме матриц слагаемых.
Определение 7
Произведением оператора на число a именуется оператор такойC, что C х = a( х).ОбозначаетсяC = a .
К примеру, в случае, если : R2®R2 таковой, что х = [х1, х2]IR2 х = [х1+х2, 2х2], то преобразование ( ) определяет вектор
у = 3( х) = 3[х1+х2, 2х2] = [3х1+3х2, 6х2].
Докажите, что:
1) В случае, если преобразование – линейное, то и a – линейное преобразование.
2) Матрица преобразования C = a равна С = aА, где А – матрица преобразования .
Применяя умножения сложения преобразования и операции преобразований на число, возможно выяснить операцию вычитания преобразований:
( – )х = ( +(– ))х = х – х.
Матрица для того чтобы преобразования, разумеется, равна А – В.
Определение 8
Произведением (композицией) преобразований и именуется преобразование C, определяемое равенством Cх = ( х).Обозначается произведение преобразований C = .
Из определения направляться, что умножение преобразований свидетельствует последовательное их использование.
К примеру, в случае, если преобразование :R2®R2 такое, что х=[х1, х2]IR2 х = [х1+х2, 2х2], а преобразование :R2®R2такое, что х = [х1, х2]IR2 = [3х1, х1 – 2х2], то преобразование C = . каждому х = [х1, х2]IR2 ставит в соответствие вектор
C х = ( х) = ([3х1, х1 –2х2]) = [3х1 + (х1 – 2х2), 2(х1 –2х2)] =
= [ 4×1 – 2×2, 2×1– 4×2].
Увидим, что преобразование , по большому счету говоря, не сходится с преобразованием .
Вправду, к примеру, для рассмотренных выше преобразований и отыщем преобразование C1 = :
C1 х = ( х) = ([х1+х2, 2х2]) = [3(х1 + х1) , х1+х2 – 2(2х2)] =
= [ 3×1 +3×2, x1– 3×2].
Разумеется, C х ? C1 х.
Пользуясь определением произведения преобразований, возможно разглядывать «п-ю степень» преобразования, как последовательное использование этого преобразования п раз:
2х = ( х), 3х = ( ( х)), и т.д.
Докажите, что в случае, если и – линейные преобразования, то и – линейное преобразование.
Пускай линейного пространства и преобразования L в некоем базисе Б имеют соответственно матрицы А и В. Отыщем матрицу С преобразования C = в этом же базисе. Обозначим:
Х – координатный столбец произвольного вектора х пространства L в базисе Б,
У – координатный столбец вектора х в этом же базисе,
Z – координатный столбец вектора ( х).
Тогда У = ВХ, Z = АУ, Z = СХ. Из этого имеем
Z = АУ = А(ВХ) = (АВ)Х и Z = СХ ,
значит, С =А.В.
Так, матрица произведения преобразований равна соответствующему произведению матриц преобразований-сомножителей.
Матрица преобразования п (п – натуральное число) равна, разумеется, Ап.
Разглядим еще один пример.
Пример 4
По этому вектору IV2 выстроить векторы ( + ) и ( . ) , в случае, если – симметрия относительно оси ОХ, а – поворот плоскости на 180о около начала координат против часовой стрелки. Записать матрицы всех этих преобразований в каком-либо базисе.
Пускай – произвольный вектор плоскости, и (х, у) – его координаты в ортонормированном базисе . По условию (рисунок 1) имеем
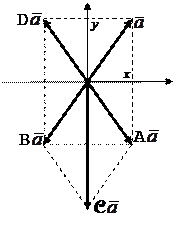= (х, – у), = (– х, – у).
Обозначим C = + и = . . Тогда
C = ( + ) = (х, – у) + (– х, – у) = (0,–2у),
= ( . ) = ( ) = ((–х), –(–у)) = (– х, у)
| Рисунок 1 |
(последнее преобразование имеется, разумеется, симметрия довольно ОУ).
Отыщем матрицы этих преобразований в выбранном базисе , для чего отыщем координаты образов базовых векторов в этом базисе.
= (1, 0) ? , , C = ( + ) = (0, 0),
=( . ) = (–1, 0),
= (0, 1) ? = (0, –1), = (0, –1), C = ( + ) = (0, –2),
= ( . ) = (0, 1).
Значит,
А =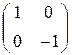 
, В = 
,
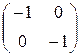С =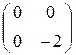 
(сравните с А+В), D = 
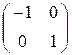(сравните с АВ).
Увидим, что преобразование C = + – вырожденное.
Разглядим невырожденное преобразование .
Определение 9
Преобразование –1 , переводящее любой вектор х в вектор х, именуется обратным кпреобразованию линейного пространства L.
Возможно продемонстрировать, что справедливо равенство
. –1 = –1. = .
В случае, если невырожденное преобразование в некоем базисе задается невырожденной матрицей А, то обратное преобразование –1 задается в этом базисе матрицей А–1.
Преобразование, владеющее обратным, именуется обратимым преобразованием.
В случае, если обратимое преобразование – линейное, то обратное преобразование –1 кроме этого линейное, т.к., в соответствии с определению 9,
–1( + ) = –1( ) = = –1( )+ –1( ),
–1(l ) = –1( ) = =l –1( ).
Разумеется, тождественный оператор есть обратным самому себе.
Из взятых результатов направляться, что операции над линейными преобразованиями владеют теми же особенностями, что и операции над матрицами, к примеру, сложение коммутативно и ассоциативно:
+ = + , +( + C ) = ( + ) + C ;
умножение ассоциативно, но не коммутативно:
C ( ) = (C ) , ? .
Тождественное преобразование играется среди преобразований роль единицы, а нулевое – роль нуля.
собственные значения и Собственные векторы линейного преобразования
Пускай дана квадратная матрица порядка п
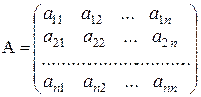
Составим для нее матрицу
(А – lЕ) =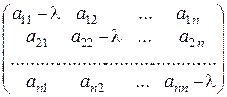 
где l – произвольное число, а Е – единичная матрица. Матрица (А – lЕ) именуется характеристической матрицей матрицы А, а уравнение
| А–lЕ | = 0 либо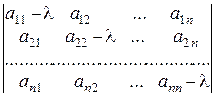 
= 0
именуется характеристическим уравнением матрицы А.
Разумеется, определитель | A – lЕ | есть многочленом степени п довольно l. Данный многочлен кроме этого именуют характеристическим многочленом матрицы А, корни этого многочлена именуются характеристическими корнями(числами) матрицы А.
Возможно доказать, что подобные матрицы владеют однообразными характеристическими многочленами, а, значит, и однообразные характеристические корни.
Как мы знаем, между линейными преобразованиями и квадратными матрицами существует взаимно однозначное соответствие, причем матрицы, задающие линейное преобразование в различных базисах, подобны. Значит, не смотря на то, что линейное преобразование в различных базисах задается разными матрицами, но все эти матрицы имеют одинаковый комплект характеристических корней. Исходя из этого характеристические корни матрицы преобразования именуют характеристическими корнями самого преобразования. Разглядим одно из применений характеристических корней преобразования.
Определение 10
ПустьLn – линейное пространство, :Ln ® Ln – линейное преобразование этого пространства. Ненулевой вектор и именуется собственным вектором линейного преобразования , если он этим преобразованием переводится в вектор lи, т.е.
и = lи,
где самоё – некоторое настоящее число. Наряду с этим l именуется собственным числом либо собственным значением линейного преобразования , соответствующим собственному вектору и.
Потому, что между матрицами и линейными преобразованиями в заданном базисе существует взаимно однозначное соответствие, то введенные понятия смогут быть отнесены и к матрицам. Так, в случае, если А – квадратная матрица (матрица линейного преобразования в некоем базисе), Х – матрица-столбец координат вектора и ¹ 0 (в этом же базисе), то данный вектор именуется собственным вектором матрицы А, а число l – собственным числом данной матрицы, в случае, если АХ = lХ.
Пускай и – личный вектор линейного преобразования , заданного в некоем базисе Б матрицей А, l – соответствующее этому вектору собственное значение, т.е. и= lи, и ¹ 0. Обозначим Х =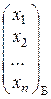 
– координатный столбец вектора и в базисе Б, тогда в матричном виде равенство и= lи запишется так
АХ = lХ ? АХ – lХ = О, (А – lЕ)Х = О.
В случае, если А =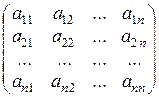 
, то А – lЕ = 
,
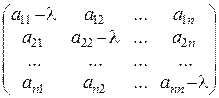и равенство (А – lЕ)Х = О равносильно совокупности линейных уравнений
(*)
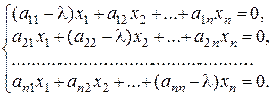Потому, что Х – ненулевая матрица-столбец, то эта совокупность имеет непростое ответ, что допустимо только в том случае, в то время, когда определитель главной матрицы данной совокупности равен нулю, т.е. в то время, когда выполняется условие .
Следовательно, личные значения l преобразования (либо матрицы А) имеется корни уравнения , т.е. настоящие характеристические корни этого преобразования (матрицы).
Напротив, пускай l0 – характеристический корень преобразования , т.е. l0 есть корнем характеристического многочлена . Тогда при l = l0 определитель совокупности (*) равен нулю, следовательно, совокупность имеет непростое ответ. Потому, что совокупность (*) равносильна матричному уравнению , либо , то ответ совокупности имеется столбец Х=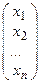 
, что возможно разглядывать как координатный столбец вектора и, удовлетворяющего равенству и = l0и, т.е. собственного вектора преобразования , соответствующего собственному значению l0.
Так мы доказали, что настоящие характеристические корни линейного преобразования, если они существуют, и лишь они являются собственными значениями этого преобразования.
Собственное значение называетсят-кратным, если оно есть т-кратным корнем характеристического уравнения. В случае, если собственное значение – несложной корень характеристического уравнения, то его именуют простымсобственным значением.
Из сказанного выше вытекает метод нахождения собственных собственных векторов и значений преобразования :
1. Выбирают в заданном линейном пространстве произвольный базис.
2. Находят матрицу А преобразования в этом базисе.
3. Находят характеристические числа преобразования , решив уравнение
, т.е.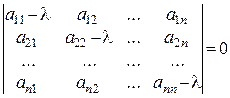 
и выбирают из них настоящие, каковые и являются собственными значениями. В случае, если нет настоящих характеристических корней, то нет ни собственных значений, ни собственных векторов.
4. Составляют совокупность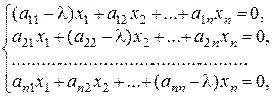 
(7.1)
и, полагая l равным одному из отысканных собственных значений li, находят ненулевое ответ Хi =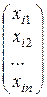 
данной совокупности. Полученный вектор иi = Хi = 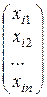и имеется личный вектор, соответствующий забранному собственному значению li.
5. Пункт 4 этого метода повторяют для каждого собственного значения.
Обратите внимание, что потому, что для каждого собственного значения li совокупность (7. 1) имеет множество ответов, то для данного преобразования существует нескончаемое число собственных векторов, соответствующих собственному числу li.
Пример 6
Отыскать личные векторы преобразования , заданного матрицей А =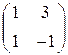 
.
Ответ
Пункты 1 и 2 указанного метода уже выполнены. Разглядим сходу третий пункт. Составим характеристическое уравнение и отыщем его корни:
= 
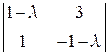= – (1–l)(1+l) –3 = – (1–l2) – 3 = l2 – 4,
l2 – 4 = 0 ? l1 = 2, l2 = –2.
Это настоящие числа, значит, они являются собственными значениями.
Составим совокупность вида (7.1):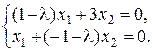 
Отыщем решения данной совокупности для каждого из взятых собственных значений.
При возьмём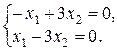 
Ранг данной совокупности, разумеется, равен 1, значит, совокупность равносильна одному уравнению , решая которое, находим х1 = 3х2. Положим х2 = t, возьмём x1 = 3t, тогда личный вектор и1 = (3t, t) соответствует собственному значению .
При возьмём совокупность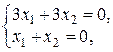 
ранг которой кроме этого равен 1, исходя из этого она равносильна уравнению х1 + х2 = 0, откуда х1 = – х2.При , возьмём , откуда имеем личный вектор и2 = (–s, s), соответствующий собственному значению l1 = – 2.
Так, имеем семейство собственных векторов и1 = (3t, t), соответствующих собственному числу l1 = 2 и семейство собственных векторов и2 = (– s, s) , соответствующих собственному числу l1 = – 2.