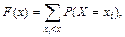Тема 3. Случайная величина.
Дискретные случайные размеры
Случайная величина
Выше рассматривались случайные события, являющиеся качественной чёртом случайного результата опыта. Для получения количественной характеристики вводится понятие случайной величины.
Определение.Случайной величинойназывается величина, которая в следствии опыта может принимать каждые заблаговременно малоизвестные значения.
Примеры.
1) В студенческой группе 25 человек. Пускай величина Х – число студентов, находящихся в аудитории перед занятиями . Ее вероятными значениями будут числа 0, 1, 2,…,25. При каждом опробовании (начало занятий) величина Х непременно примет одно из собственных вероятных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.
2)Измерение курса акции некоего предприятия. Вероятные события заключаются в том, что курс акции Y примет некое значение в пределах от 0 до ?.
Случайные размеры возможно поделить на две категории: дискретные и постоянные.
Определение. Дискретной случайной величиной именуется такая величина, которая в следствии опыта может принимать определенные значения, образующие счетное множество (множество, элементы которого смогут быть занумерованы).
Это множество возможно как конечным, так и нескончаемым.
К примеру, количество выстрелов до первого попадания в цель есть дискретной случайной величиной, т.к. эта величина может принимать и нескончаемое, не смотря на то, что и счетное количество значений.
Для задания случайной величины слишком мало ее значение, нужно кроме этого указать возможность этого значения.
функция и Закон распределения дискретной случайной величины
Определение. Соотношение между вероятными значениями случайной величины и их возможностями именуется законом распределения дискретнойслучайной величины.
Закон распределения возможно задан аналитически, в виде таблицы либо графически.
Таблица соответствия значений случайной их вероятностей и величины именуется рядом распределения.
| Х | х1 | х2 | … | хn | … |
| Р | р1 | р2 | … | рn | … |
События образуют полную группу попарно свободных событий. Следовательно, .
Графическое представление данной таблицы именуется многоугольником распределения. Наряду с этим сумма всех ординат многоугольника распределения является вероятностью всех вероятных значений случайной величины, а, следовательно, равна единице.
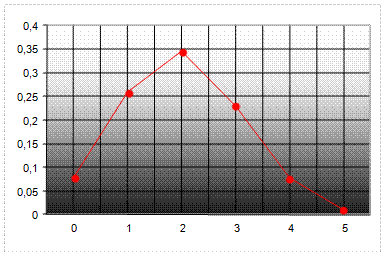
Пример. По цели производится 5 выстрелов. Возможность попадания для каждого выстрела равна 0,4. Отыскать возможности числа попаданий и выстроить многоугольник распределения.
Возможности пяти попаданий из пяти вероятных, четырех из пяти и трех из пяти были отысканы выше по формуле Бернулли и равны соответственно:
, ,
Подобно отыщем:
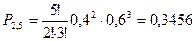
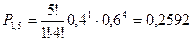
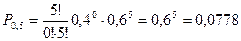
Тогда закон распределения имеет форму:
| Х | 0 | 1 | 2 | 3 | 4 | 6 |
| Р | 0,0778 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,01024 |
Представим графически зависимость числа попаданий от их возможностей.
 |
Функция распределения содержит все данные о случайной величине. На практике функцию распределения не всегда возможно установить; время от времени для того чтобы исчерпывающего знания и не нужно.
Функция распределения дискретной случайной величины равна возможности случайного события, пребывающего в том, что дискретная случайная величина X примет одно из вероятных значений, меньших некоего значения x, т.е.
В случае, если дискретные значения случайной величины находятся в порядке возрастания то возможно записать в виде
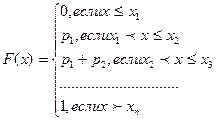
Функция распределения владеет следующими особенностями:
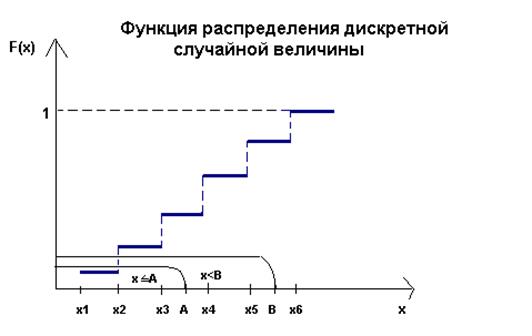
1. Значение функции распределения в собственности отрезку [0,1]: 0?F(x)?1.
2. Функции распределения имеется неубывающая функция.
3. Возможность того, что случайная величина Х примет значение, заключенное в промежутке (а, b), равна приращению функции распределения на этом промежутке:
Р(а
4. В случае, если все вероятные значения случайной величины Х принадлежат промежутку (а, b), то
F(x) = 0 при х?а;?F(x) = 1 при х³b.
5. Честны следующие предельные отношения:
.
Для дискретной случайной величины Х, которая может принимать значения х1, х2, …,хn, функция распределения имеет форму