Вектор – это направленный отрезок прямой, обозначается 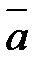 либо
либо 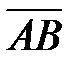 . Точка
. Точка 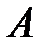 — начало вектора, точка
— начало вектора, точка 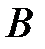 — его финиш. Длиной либо модулем вектора
— его финиш. Длиной либо модулем вектора 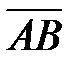 именуется протяженность отрезка
именуется протяженность отрезка 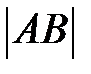 и обозначается
и обозначается 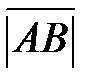 . Вектор, протяженность которого равна нулю, именуется нулевым вектором и обозначается
. Вектор, протяженность которого равна нулю, именуется нулевым вектором и обозначается 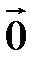 . Вектор, имеющий длина и
. Вектор, имеющий длина и 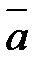 направление вектора которого равна 1, именуется единичным вектором либо ортом вектора
направление вектора которого равна 1, именуется единичным вектором либо ортом вектора 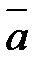 и обозначается
и обозначается 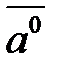 .
.
Векторы 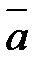 и
и 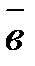 именуются коллинеарными, если они лежат на одной прямой либо на параллельных прямых. Записывается так
именуются коллинеарными, если они лежат на одной прямой либо на параллельных прямых. Записывается так 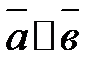 . Два вектора именуются равными, если они одинаково направлены и имеют однообразные длины.
. Два вектора именуются равными, если они одинаково направлены и имеют однообразные длины.
Три вектора в пространстве именуются компланарными, если они лежат в одной либо параллельных плоскостях.
Под линейными операциями над векторами знают умножение сложения вектора и операцию векторов 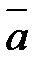 на настоящее число
на настоящее число 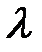 .
.
Суммой двух векторов 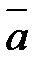 и
и 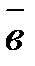 именуется вектор
именуется вектор 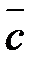 , соединяющий начало первого вектора
, соединяющий начало первого вектора 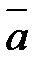 с финишем второго вектора
с финишем второго вектора 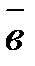 , при условии, что конец вектора
, при условии, что конец вектора 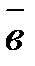 и начало вектора
и начало вектора 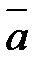 совмещены. Обозначается сумма
совмещены. Обозначается сумма 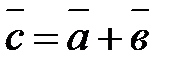 . Рис.4.
. Рис.4.
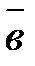
|
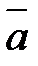
|
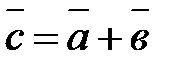
|
Рис. 4.
Такое правило сложения векторов именуется правилом треугольника. Два вектора возможно сложить и по правилу параллелограмма. Рис.5.
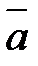
|
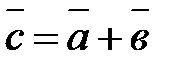
|
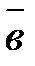
|
Рис. 5.
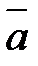
|
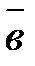
|
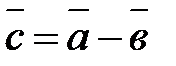
|
Разность двух векторов 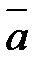 и
и 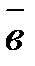 именуется третий вектор
именуется третий вектор 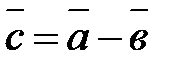 , таковой, что
, таковой, что 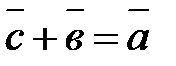 . Рис.6.
. Рис.6.
Рис. 6.
Произведение вектора 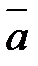 на число
на число 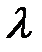 именуется вектор
именуется вектор 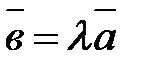 , протяженность которого равна
, протяженность которого равна 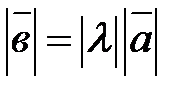 , он коллинеарен вектору
, он коллинеарен вектору 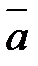 и имеет направление вектора
и имеет направление вектора 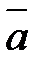 , в случае, если
, в случае, если 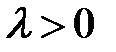 , и противоположное, в случае, если
, и противоположное, в случае, если 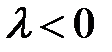 .
.
Линейные операции над векторами владеют следующими особенностями:
1. 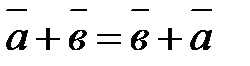
2. 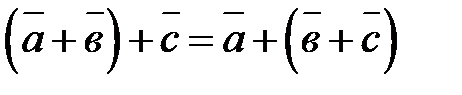
3. 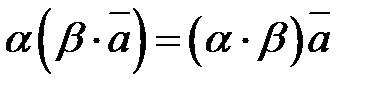
4. 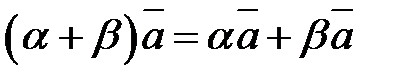
5. 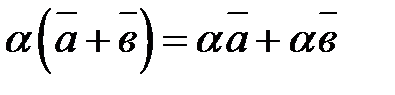
Нужным и достаточным условием коллинеарности двух векторов 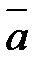 и
и 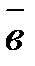 есть существование для того чтобы числа
есть существование для того чтобы числа 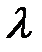 , что
, что 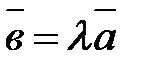 .
.
Линейной комбинацией векторов 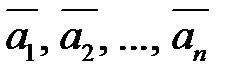 именуется сумма произведений этих векторов на настоящие числа:
именуется сумма произведений этих векторов на настоящие числа:
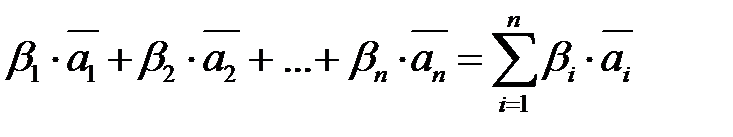 (7.1).
(7.1).
Совокупность векторов 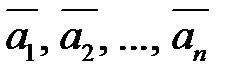 именуется линейно свободной, в случае, если их линейная комбинация (7.1) равна нулю лишь при всех
именуется линейно свободной, в случае, если их линейная комбинация (7.1) равна нулю лишь при всех 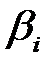 одновременно равных нулю.
одновременно равных нулю.
Два вектора 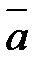 и
и 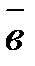 образуют базис на плоскости, в случае, если любой третий вектор
образуют базис на плоскости, в случае, если любой третий вектор 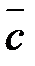 на плоскости возможно представить в виде
на плоскости возможно представить в виде
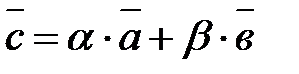 (7.2).
(7.2).
Три вектора 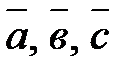 образуют базис в пространстве, в случае, если любой вектор
образуют базис в пространстве, в случае, если любой вектор 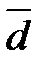 этого пространства возможно представить в виде:
этого пространства возможно представить в виде:
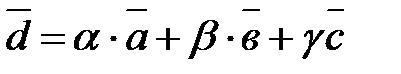 (7.3).
(7.3).
Выражение (7.3) именуют разложением вектора  по базису из векторов
по базису из векторов  , а числа
, а числа  именуют координатами вектора
именуют координатами вектора 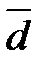 в базисе
в базисе 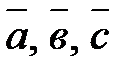 . Условно это записывается
. Условно это записывается 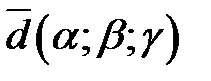 .
.
Два неколлинеарных вектора образуют базис на плоскости, три некомпланарных вектора образуют базис в пространстве.
В случае, если известны координаты векторов в некоем базисе, то линейные операции над векторами сводятся к простым арифметическим операциям над координатами этих векторов.
Дабы сложить два вектора необходимо сложить их соответствующие координаты.
Дабы отыскать разность двух векторов нужно отыскать разность их соответствующих координат.
Дабы умножить вектор на настоящее число, нужно умножить каждую его координату на это число.
Честны следующие утверждения. Два вектора равны, в случае, если равны их соответствующие координаты. Два вектора коллинеарны, в случае, если их координаты пропорциональны.
Пример 10. Даны векторы 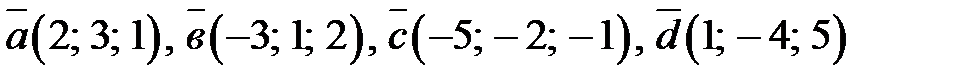 . Проверить, что векторы
. Проверить, что векторы 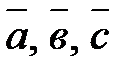 образуют базис и отыскать координаты вектора
образуют базис и отыскать координаты вектора 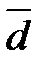 в этом базисе.
в этом базисе.
Ответ. Составим линейную комбинацию векторов 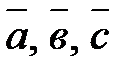 и приравняем ее к нулю:
и приравняем ее к нулю: 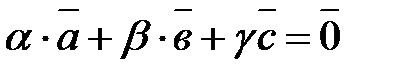 . Продемонстрируем, что это равенство справедливо только при условии
. Продемонстрируем, что это равенство справедливо только при условии 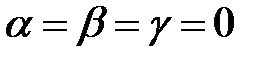 . Из равенства векторов направляться:
. Из равенства векторов направляться:
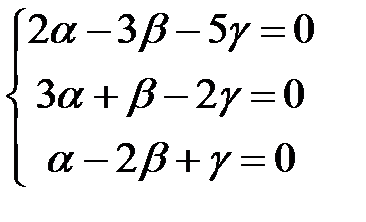
Отыщем определитель взятой однородной совокупности:
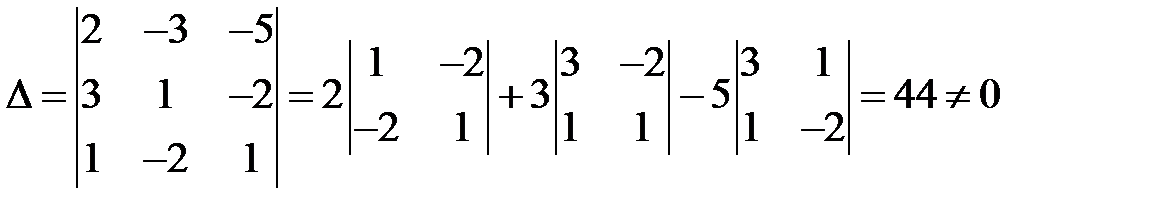
Следовательно, совокупность имеет единственное ответ 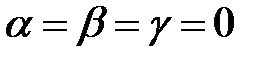 :
:
а это значит, что векторы 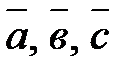 — образуют базис.
— образуют базис.
Отыщем координаты вектора 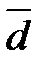 в этом базисе.
в этом базисе.
Запишем векторное равенство:
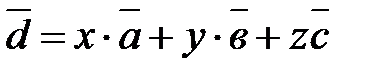 .
.
Переходя к координатой форме, возьмём:
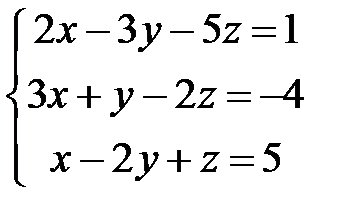
Решив эту совокупность, возьмём:
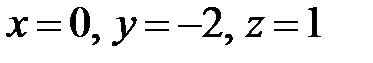 .
.
Тогда 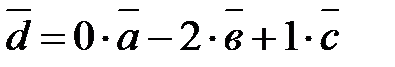 , либо
, либо 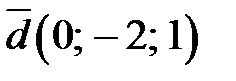 в базисе
в базисе  .
.
В прямоугольной совокупности координат 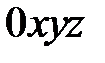 любой вектор
любой вектор 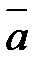 возможно представить в виде
возможно представить в виде
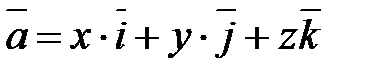 (7.4),
(7.4),
где 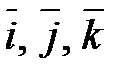 — взаимно ортогональные единичные векторы осей координат
— взаимно ортогональные единичные векторы осей координат 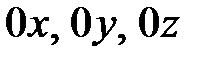 .
.
Координатами вектора 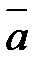 в прямоугольной совокупности координат являются проекции этого вектора на соответствующие оси координат, другими словами
в прямоугольной совокупности координат являются проекции этого вектора на соответствующие оси координат, другими словами
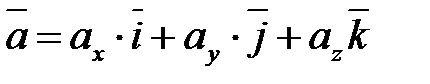 (7.5).
(7.5).
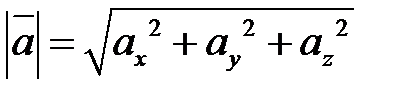 — протяженность вектора
— протяженность вектора 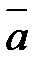 в прямоугольной совокупности координат.
в прямоугольной совокупности координат.
Углы, каковые вектор 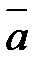 образует с осями координат, принято обозначать соответственно
образует с осями координат, принято обозначать соответственно 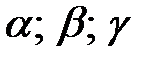 . Косинусы этих углов именуют направляющими косинусами вектора
. Косинусы этих углов именуют направляющими косинусами вектора 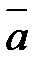 . Направляющие косинусы равны соответственно:
. Направляющие косинусы равны соответственно:
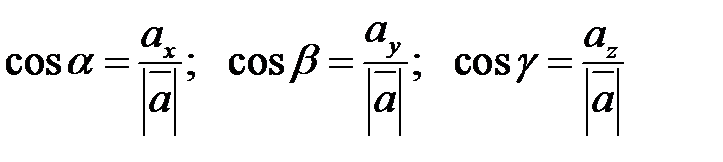 (7.6),
(7.6),
Либо в координатной форме:
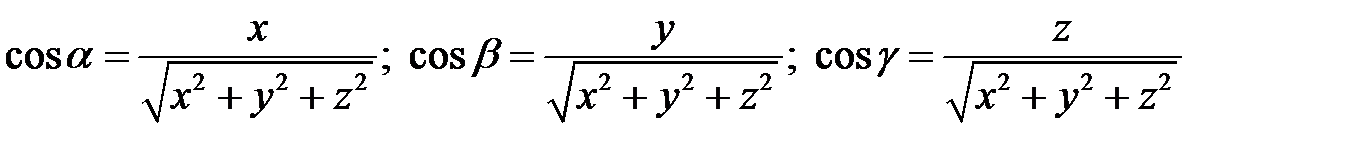 .
.
Для направляющих косинусов выполняется равенство
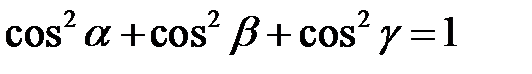 (7.7).
(7.7).
В случае, если известны координаты точек 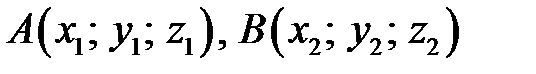 то координаты вектора
то координаты вектора 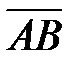 определяются формулами
определяются формулами 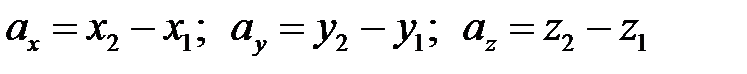 , другими словами
, другими словами
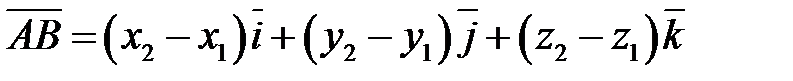 .
.
Умножение векторов
Векторы возможно умножать скалярно и векторно. Скалярным произведением двух ненулевых векторов 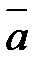 и
и 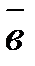 именуется число, равное произведению длин этих векторов на косинус угла между ними:
именуется число, равное произведению длин этих векторов на косинус угла между ними:
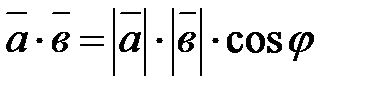 (8.1).
(8.1).
Эту формулу возможно записать в виде
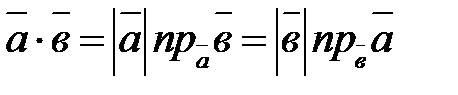 .
.
Скалярное произведение имеет следующие особенности:
1. 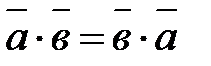 — переместительный закон.
— переместительный закон.
2. 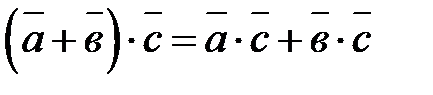 — распределительный закон
— распределительный закон
3. 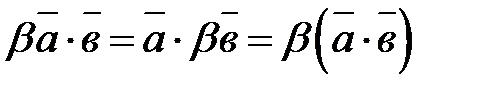
4. 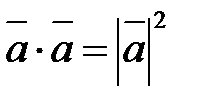 , из этого
, из этого 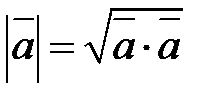
5. В случае, если 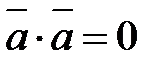 , то
, то 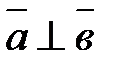 — условие перпендикулярности векторов
— условие перпендикулярности векторов 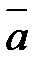 и
и 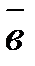
6. 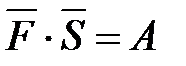 ,
, 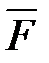 — вектор силы,
— вектор силы, 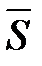 — вектор перемещения,
— вектор перемещения, 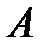 — работа силы
— работа силы 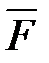 .
.
В случае, если 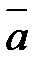 и
и 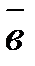 заданы в прямоугольной совокупности координат
заданы в прямоугольной совокупности координат 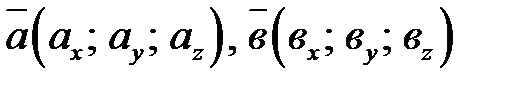 , то
, то 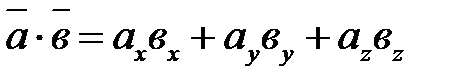 (8.2).
(8.2).
Упорядоченная тройка векторов 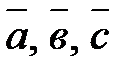 именуется правой, в случае, если малейший поворот от вектора
именуется правой, в случае, если малейший поворот от вектора 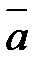 к вектору
к вектору 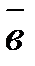 из финиша вектора
из финиша вектора 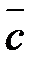 виден совершающимся против часовой стрелки. Рис.7.
виден совершающимся против часовой стрелки. Рис.7.
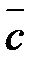
|
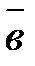
|
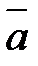
|
Рис. 7.
Векторным произведением вектора 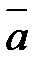 на вектор
на вектор 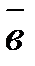 именуется третий вектор
именуется третий вектор 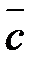 , протяженность которого равна
, протяженность которого равна 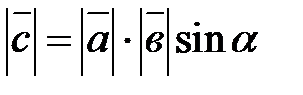 , он перпендикулярен векторам
, он перпендикулярен векторам 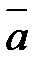 и
и 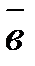 и направлен в ту сторону, что векторы
и направлен в ту сторону, что векторы 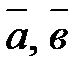 и
и 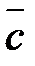 образуют правую тройку.
образуют правую тройку.
Векторное произведение обозначается 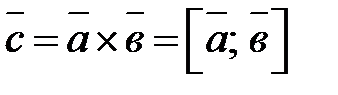 .
.
Векторное произведение имеет следующие особенности:
1. 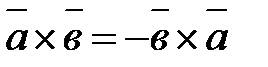
2. 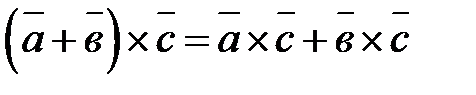
3. 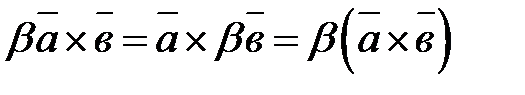
4. В случае, если 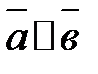 , то
, то 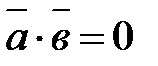
5. 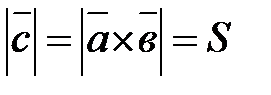 , где
, где 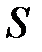 — площадь параллелограмма, выстроенного на этих векторах как на сторонах.
— площадь параллелограмма, выстроенного на этих векторах как на сторонах.
В случае, если векторы 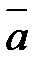 и
и 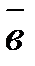 заданы в прямоугольной совокупности координат:
заданы в прямоугольной совокупности координат: 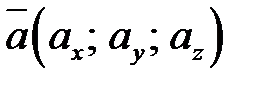 и
и 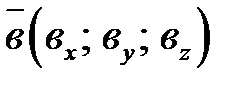 , то:
, то:
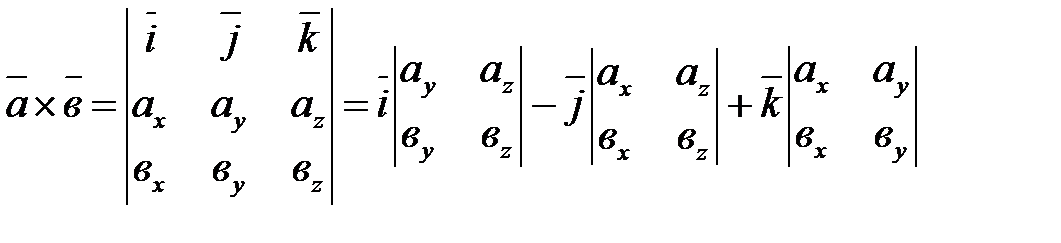 (8.3).
(8.3).
В случае, если 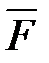 вектор силы, приложенной в точке
вектор силы, приложенной в точке 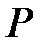 , а
, а 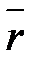 радиус-вектор точки
радиус-вектор точки 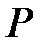 , то момент силы
, то момент силы 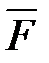 , относительно начала координат
, относительно начала координат 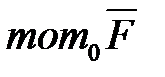 равен:
равен:
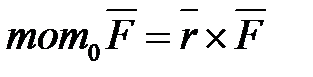 .
.
Смешанным произведением трех векторов 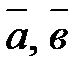 и
и 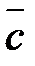 именуется их векторно-скалярное произведение. Обозначается
именуется их векторно-скалярное произведение. Обозначается 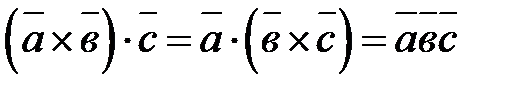 .
.
В случае, если заданы координаты векторов в прямоугольной совокупности координат, то их смешанное произведение вычисляется по формуле:
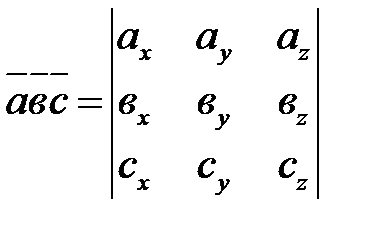 (8.4).
(8.4).
Свойства смешанного произведения векторов:
1. 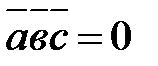 — условие компланарности векторов;
— условие компланарности векторов;
2. 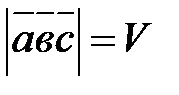 — количество параллелепипеда, выстроенного на векторах, как на сторонах;
— количество параллелепипеда, выстроенного на векторах, как на сторонах;
3. 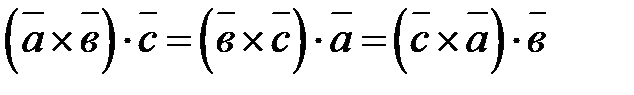 — циклическая перестановка сомножителей не меняет величины смешанного произведения;
— циклическая перестановка сомножителей не меняет величины смешанного произведения;
4. 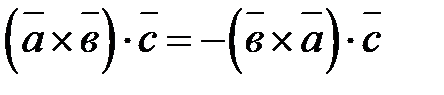
Пример 11. Даны вершины пирамиды 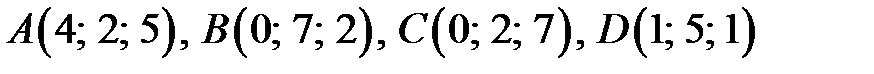 . Отыскать 1) угол между гранью
. Отыскать 1) угол между гранью 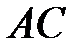 и ребром
и ребром 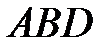 ; 2) площадь грани
; 2) площадь грани 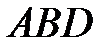 ; 3) количество пирамиды
; 3) количество пирамиды 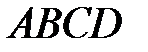 ; 4) длину высоты, опущенной из вершины
; 4) длину высоты, опущенной из вершины  на грань
на грань 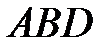 .
.
Ответ. Вычислим координаты вектора 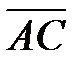 :
:
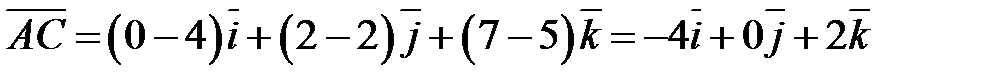 .
.
Угол 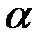 между гранью
между гранью 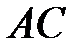 и ребром
и ребром 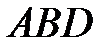 есть дополнительным углом для угла
есть дополнительным углом для угла 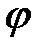 , образованного перпендикуляром, совершённым к плоскости треугольника
, образованного перпендикуляром, совершённым к плоскости треугольника 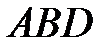 и ребром
и ребром 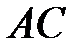 .
. 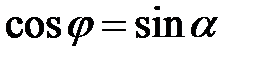 . Для нахождения
. Для нахождения 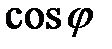 вычислим координаты векторного произведения векторов
вычислим координаты векторного произведения векторов 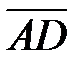 и
и 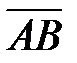 :
:
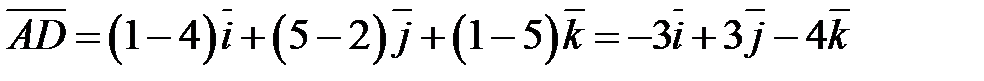 ;
;
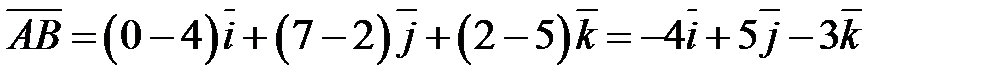 .
.
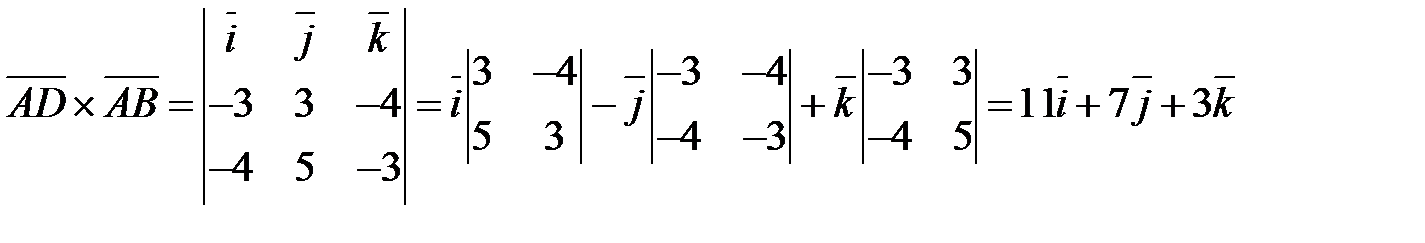 .
.
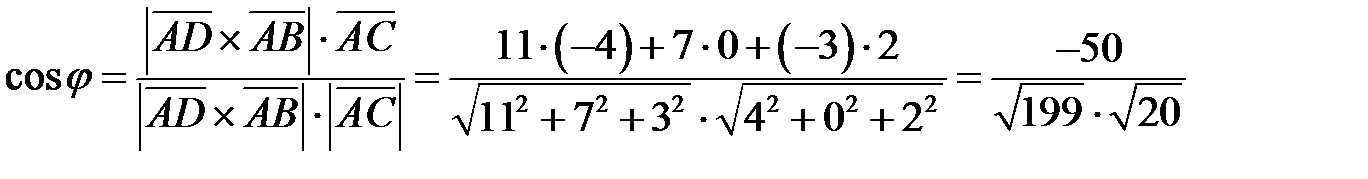 ;
;
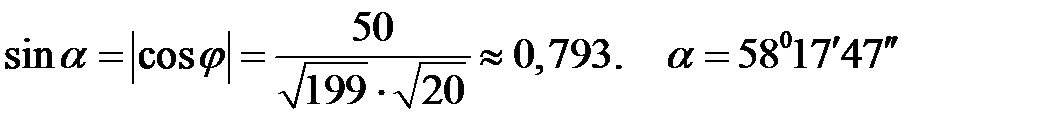 .
.
1) Площадь грани  равна половине площади параллелограмма, выстроенного на сторонах
равна половине площади параллелограмма, выстроенного на сторонах 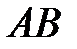 и
и 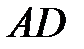 , т.е.
, т.е.
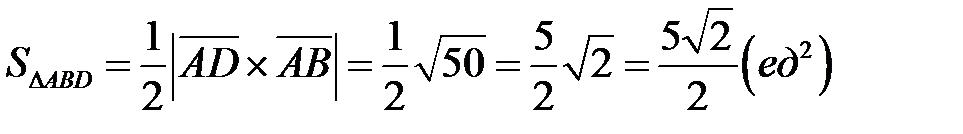 .
.
2) Количество пирамиды равен одной трети от количества параллелепипеда,
выстроенного на ребрах  и
и 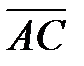 . Следовательно
. Следовательно
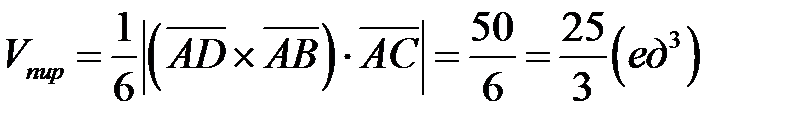 .
.
3) Протяженность высоты 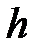 определяется из формулы:
определяется из формулы:
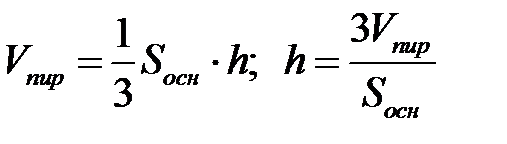 ;
; 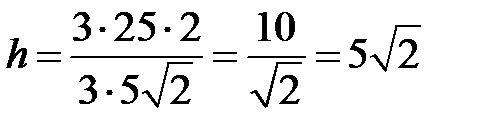 .
.
Ответ: 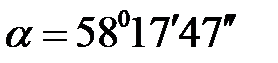 ;
; 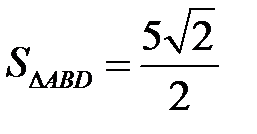 ;
; 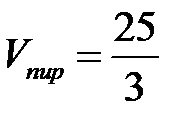 ;
; 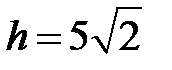 .
.
Комплексные числа
Комплексным числом 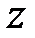 именуется выражение
именуется выражение
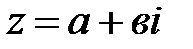 (9.1),
(9.1),
где 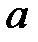 и
и 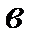 — настоящие числа; — мнимая единица, определяемая равенством
— настоящие числа; — мнимая единица, определяемая равенством
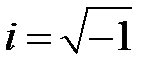 либо
либо 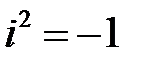 (9.2).
(9.2).
Число 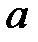 именуют настоящей частью комплексного числа
именуют настоящей частью комплексного числа 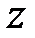 и обозначают
и обозначают 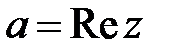 ;
;  — мнимая часть комплексного числа
— мнимая часть комплексного числа 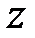 . Ее обозначают
. Ее обозначают 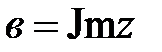 . В случае, если
. В случае, если 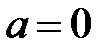 , то число
, то число 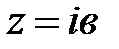 именуют чисто мнимым, в случае, если
именуют чисто мнимым, в случае, если 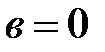 , то число
, то число 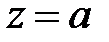 , имеется настоящее число.
, имеется настоящее число.
Два комплексных числа 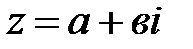 и
и 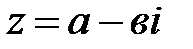 именуют комплексно сопряженными числами.
именуют комплексно сопряженными числами.
Два комплексных числа 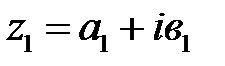 и
и 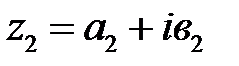 считаются равными, в случае, если
считаются равными, в случае, если 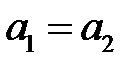 и
и 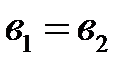 . Комплексное число
. Комплексное число 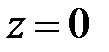 , в случае, если
, в случае, если 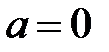 и
и 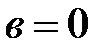 . Плоскость, точки которой изображают комплексные числа, именуется комплексной плоскостью.
. Плоскость, точки которой изображают комплексные числа, именуется комплексной плоскостью.
Время от времени комплексное число 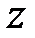 эргономичнее изображать в виде вектора
эргономичнее изображать в виде вектора 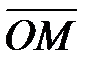 , начало которого сходится с началом координат, соединяющего точку
, начало которого сходится с началом координат, соединяющего точку 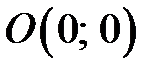 с точкой
с точкой 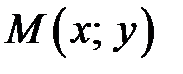 . Протяженность этого вектора именуется модулем комплексного числа
. Протяженность этого вектора именуется модулем комплексного числа 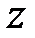 и обозначается
и обозначается 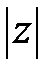 .
.
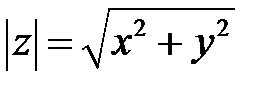 .
.
Угол 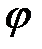 между вектором
между вектором 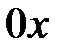 и осью
и осью 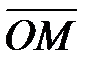 , отсчитанный против часовой стрелки, именуется доводом комплексного числа
, отсчитанный против часовой стрелки, именуется доводом комплексного числа 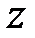 и обозначается
и обозначается 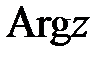 .
.
Довод числа 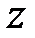 определяется с точностью до слагаемого
определяется с точностью до слагаемого 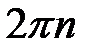 , где
, где 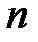 — целое число. Основное значение довода числа
— целое число. Основное значение довода числа 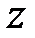 — значение довода, удовлетворяющее неравенству
— значение довода, удовлетворяющее неравенству 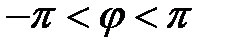 . Основное значение довода комплексного числа
. Основное значение довода комплексного числа 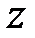 обозначается через
обозначается через 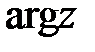 :
: 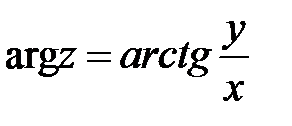 .
.
Запись числа 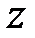 в виде
в виде 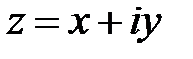 именуют алгебраической формой записи комплексного числа.
именуют алгебраической формой записи комплексного числа.
Сумма, разность комплексных чисел и умножение определяется так же, как действия над соответствующими векторами.
Суммой комплексных чисел 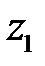 и
и 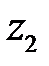 именуется комплексное число
именуется комплексное число
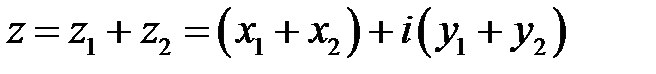 (9.3).
(9.3).
Разностью комплексных чисел 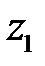 и
и 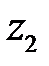 именуется комплексное число
именуется комплексное число
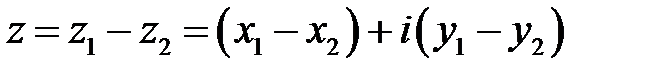 (9.4).
(9.4).
Произведение комплексного числа 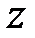 на настоящее число
на настоящее число 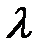 именуется комплексное число
именуется комплексное число 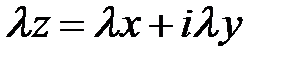 .
.
Произведение двух комплексных чисел 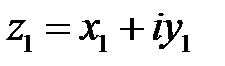 и
и 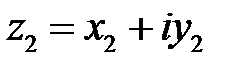 , записанных в алгебраической форме определяется как произведение двучленов:
, записанных в алгебраической форме определяется как произведение двучленов:
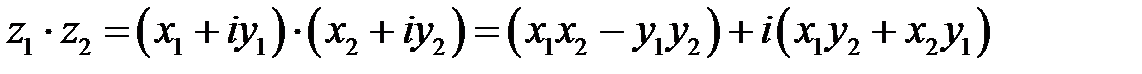 (9.5).
(9.5).
Произведением двух комплексно сопряженных чисел помогает настоящее число
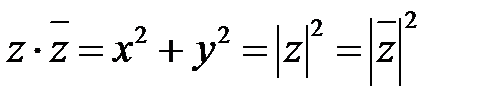 (9.6).
(9.6).
Деление комплексных чисел определяется, как воздействие обратное умножению. Частное двух комплексных чисел 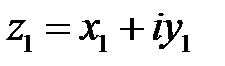 и
и 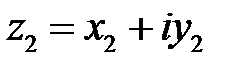 определяется следующим образом:
определяется следующим образом:
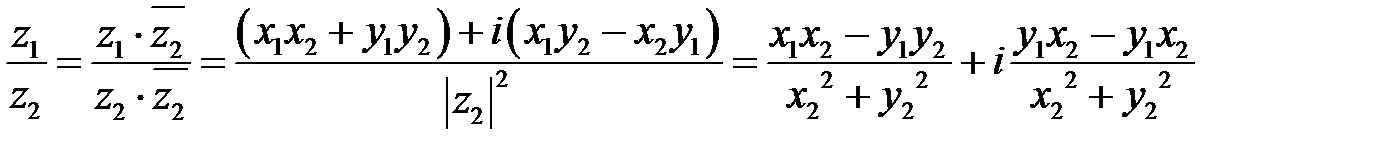 (9.7).
(9.7).
Наровне с прямоугольной совокупностью координат 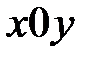 введем полярную совокупность, начало которой сходится с началом прямоугольной совокупности, а полярная ось – с хорошим направлением оси
введем полярную совокупность, начало которой сходится с началом прямоугольной совокупности, а полярная ось – с хорошим направлением оси 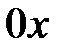 . Рис. 8.
. Рис. 8.
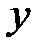
|
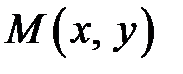
|
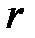
|
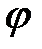
|
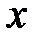
|
|
Рис. 8.
Из Рис.8 направляться, что:
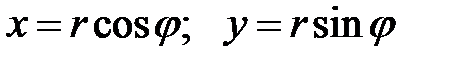 .
.
Подставляя  и
и  в алгебраическую форму комплексного числа, возьмём
в алгебраическую форму комплексного числа, возьмём
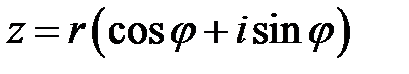 (9.8).
(9.8).
Выражение (9.8) именуют тригонометрической формой записи комплексного числа 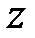 , где
, где 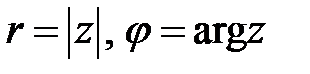 .
.
Пускай даны два комплексных числа 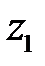 и
и 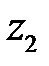 . Записанные в тригонометрической форме:
. Записанные в тригонометрической форме:
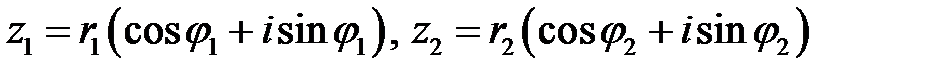 .
.
Тогда 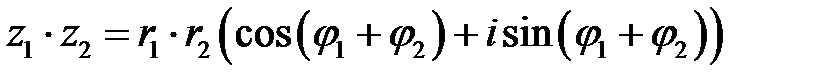 .
.
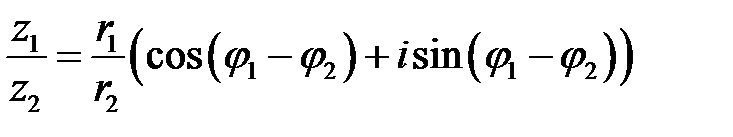 (9.9).
(9.9).
Так, при умножении комплексных чисел их модули перемножаются, а доводы складываются; при делении комплексных чисел их модули делятся, а доводы вычитаются.
В случае, если 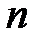 — целое положительное число, то из (9.9) направляться:
— целое положительное число, то из (9.9) направляться:
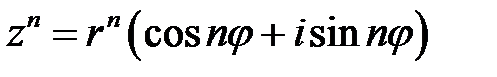 (9.10).
(9.10).
Корнем 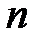 -й степени из комплексного числа
-й степени из комплексного числа 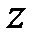 именуется такое комплексное число
именуется такое комплексное число 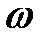 ,
, 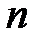 -я степень которого равна
-я степень которого равна 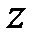 , т.е.
, т.е. 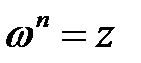 .
.
Корень 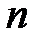 -й степени из
-й степени из 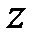 обозначается
обозначается 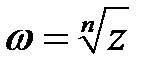 .
.
В случае, если 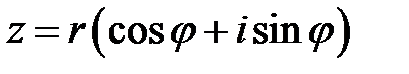 , то
, то 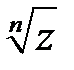 равен:
равен:
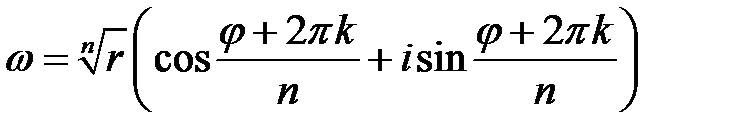 (9.11).
(9.11).
Подставляя в (9.11) значения 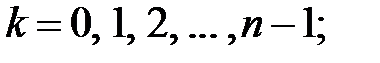 возьмём ровно
возьмём ровно 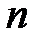 разных корней
разных корней 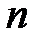 -й степени из
-й степени из 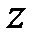 .
.
Пример 12. Дано комплексное число 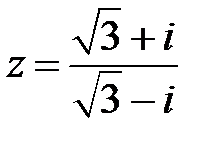 .
.
Записать число 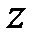 в алгебраической и тригонометрической формах. Отыскать все корни уравнения
в алгебраической и тригонометрической формах. Отыскать все корни уравнения 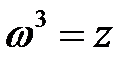 .
.
Ответ. Запишем число 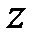 в алгебраической форме:
в алгебраической форме:
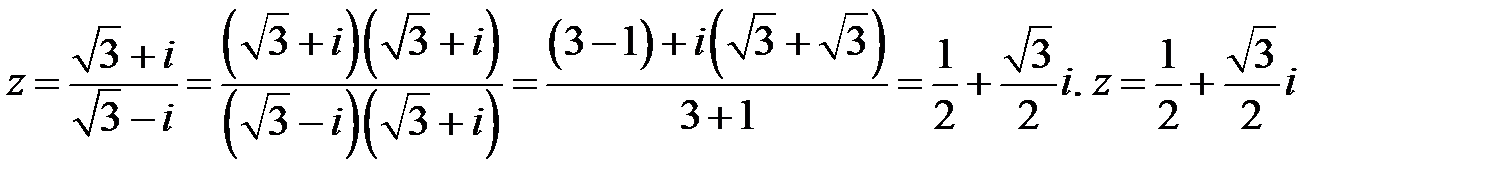 .
.
Отыщем 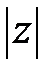 :
: 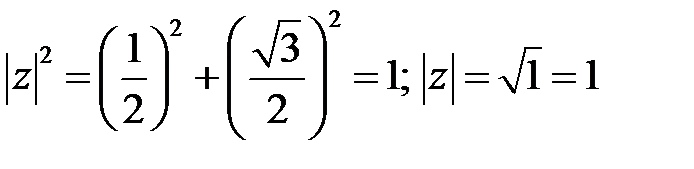 .
.
Вычислим 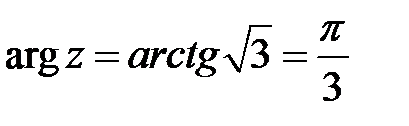 . Тригонометрическая форма записи комплексного числа
. Тригонометрическая форма записи комплексного числа 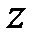 имеет форму:
имеет форму:
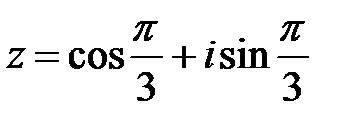 .
.
Вычислим 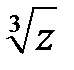 :
:
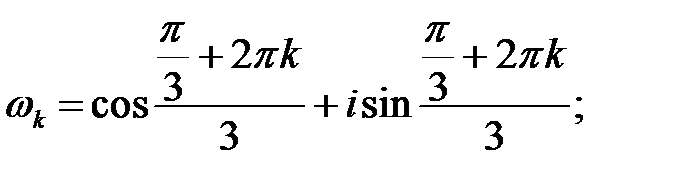
при 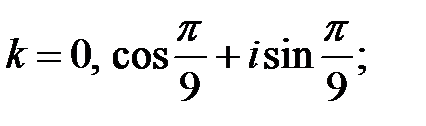
при 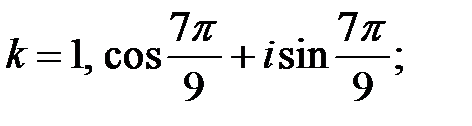
при 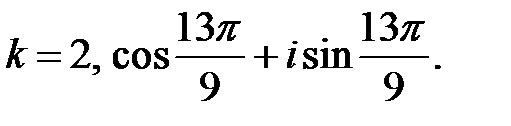
Не считая алгебраической и тригонометрической форм записи комплексного числа 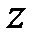 , используется более маленькая, так называемая показательная форма комплексного числа
, используется более маленькая, так называемая показательная форма комплексного числа 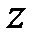 , в соответствии с которой
, в соответствии с которой
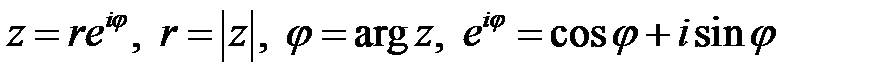 .
.
Пускай 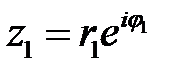 и
и 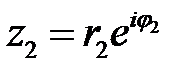 , тогда:
, тогда:
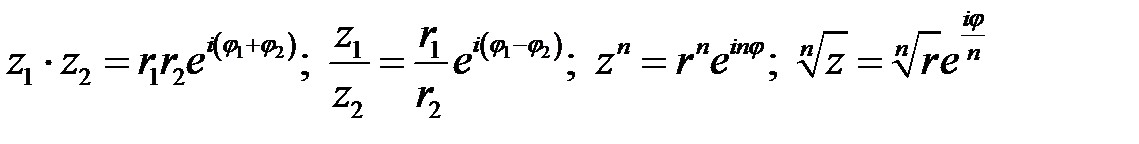 .
.