1. Выберите «Маятник».
2. Пристально разглядите рисунок, отыщите все регуляторы и другие главные элементы.
3. Установите посредством движков регуляторов большую длину нити L, значения коэффициента сопротивления b и начального угла отклонения j0, указанные в табл. 3.1 для вашего варианта.
Таблица 3.1
| Номер варианта | b, кг/с | j0, град | x0, см | m, кг | Номер варианта | b, кг/с | j0, град | x0, см | m, кг |
| 0.8 | 0.5 | 0.8 | 0.7 | ||||||
| 0.6 | 0.6 | 0.7 | 0.8 | ||||||
| 0.4 | 0.7 | 0.6 | 0.9 | ||||||
| 0.2 | 0.8 | 0.5 | 1.0 |
4. b = кг/c; = 0.
5. Нажимая мышью на кнопку «СТАРТ», смотрите за перемещением точки на графиках угла j(t) и скорости v(t) и за поведением маятника. Потренируйтесь, останавливая перемещение кнопкой «СТОП» в максимуме смещения j и запуская потом кнопкой «СТАРТ». Выберите число полных колебаний N =3¸5 и измеряйте их длительность Dt (как разность t2 – t1 из окна на экране со значениями размеров t, t, T, j,v).
6. Приступайте к измерениям длительности Dt для N (3-5) полных колебаний, начиная с большой длины L (150 см) нити маятника и уменьшая ее любой раз на 10 см (до минимальной длины 80 см). Длину нити L и результаты измерений длительности Dt записывайте в табл. 3.2. Для увеличения точности опыта совершите измерения три раза для одной и той же длины L.
Таблица 3.2
| Номер измерения | N = | ||||||
| L, м | Dt1, с | Dt2, с | Dt3, с | , с | Т, с | Т2,с2 | |
| 1,5 | |||||||
| 1,4 | |||||||
| … | … | ||||||
| 0,8 | |||||||
| g, м/с2 |
Обработка результатов измерений
1. Вычислите требуемые размеры и заполните таблицы 3.2 и 3.3.
2. Выстройте графики зависимости:
– квадрата периода колебаний Т2(L) от длины L нити математического маятника,
3. По наклону графика Т2 = f(L)определите значение ускорения свободного падения g, применяя формулу g =4p 2 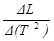 .
.
Проанализируйте графики и ответ.
5. Вычислить энергию гармонических (b=0) колебаний математического и пружинного маятников по большой потенциальной энергии: для математического маятника , , где длину подвеса L забрать из табл.3.2 соответственно, выбрав номер измерения в этих таблицах равный номеру вашего варианта.
Отчет о работе
Отчет о работе обязан содержать заполненные таблицы 3.2, графики Т2 = f(L) , расчеты g, Е.
Контрольные вопросы
1.Что такое колебание?
2.Дайте определение периода колебаний.
3.Дайте определение частоты колебаний.
4.Дайте определение гармонических колебаний.
5.Запишите закон зависимости от времени величины s, совершающей гармоническое колебательное изменение.
6.Запишите закон перемещения МТ, совершающей гармонические колебания.
7.Дайте определение амплитуды гармонических колебаний.
8.Дайте определение фазы гармонических колебаний.
9.Дайте определение начальной фазы гармонических колебаний.
10.Напишите уравнение периода и связи частоты гармонических колебаний.
11.Напишите уравнение циклической частоты и связи частоты гармонических колебаний.
12.Напишите формулу зависимости скорости МТ от времени при гармонических колебаниях.
13.Напишите уравнения амплитуды амплитуды смещения и связи скорости при гармонических колебаниях МТ.
14.Напишите формулу зависимости ускорения МТ от времени при гармонических колебаниях.
15.Напишите уравнения амплитуды амплитуды ускорения и связи скорости при гармонических колебаниях МТ.
16.Напишите уравнения амплитуды амплитуды ускорения и связи смещения при гармонических колебаниях МТ.
17.Напишите дифференциальное уравнение свободных гармонических колебаний МТ.
18.Напишите дифференциальное уравнение свободных затухающих колебаний МТ.
19.Что определяет коэффициент затухания?
20.Дайте определение математического маятника.
21.Запишите формулу циклической частоты свободных колебаний математического маятника.
22.Дайте определение пружинного маятника.
23.Запишите формулу циклической частоты свободных колебаний пружинного маятника.
24.Напишите формулу потенциальной энергии пружинного маятника.
Литература
1. Трофимова Т. И., Курс физики, М., Верховная школа, 2004 (1998). с.255-261; 267-271.
2. Детлаф А. А., Яворский Б. М. Курс физики: Учеб. пособ. для втузов. – М.: Высш. шк., 2000. С. 358-363; 371-374.
[1] Совокупность именуется линейной, в случае, если параметры, характеризующие физические особенности совокупности не изменяются на протяжении процесса. Линейные совокупности описываются линейными дифференциальными уравнениями. Пружинный маятник, движущийся в вязкой среде, представляет собой линейную совокупность, в случае, если упругость сопротивления пружины и коэффициент среды остаются постоянными.
