Теорема. Возможность суммы двух совместимых событий А и В равна сумме возможностей этих событий без возможности их произведения:
Р(А + В) = Р(А) + Р(В) – Р(АВ). (6)
Подтверждение. Пускай из всего числа n элементарных событий kблагоприятствуют событию А, l – событию B и m – в один момент событиям А и B. Из этого событию А + Вблагоприятствуют k + l – mэлементарных событий. Тогда
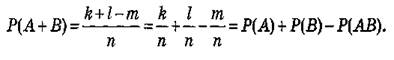
Замечание. В случае, если события A и Внесовместимы, то их произведение ABесть неосуществимое событие, и, следовательно, Р (АВ) = 0, т. е. формула (1) есть частным случаем формулы (6).
Пример 1. Возможности попадания в цель при стрельбе первого и второго орудий соответственно равны Р(А) = 0,7 и Р(В) = 0,8. Отыскать возможность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Ответ: Разумеется, события А и В совместимы и свободны. Исходя из этого
Р(А + В) = Р(А) + Р(В) – Р(АВ) = 0,7 + 0,8 – 0,7 • 0,8 = 0,94.
Пример 2. Два стрелка стреляют в одну и ту же цель, причем возможность поражения цели первым стрелком 0,8, а вторым стрелком 0,5. Оба стрелка стреляют по команде (т.е. в один момент) один раз. Какова возможность, что цель будет поражена хотя бы одним из стрелков?
Ответ: Пускай А – попадание в цель первым стрелком, В – вторым стрелком, А + В – поражение цели хотя бы одним стрелком.
События А и В совместимы и свободны. Исходя из этого Р(А + В) = Р(А) + Р(В) – Р(АВ)
Р(А + В) = Р(А) + Р(В) – Р(АВ) = 0,8 + 0,5 – 0,8 • 0,5 = 0,9.
4. Формула полной возможности.
|
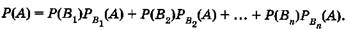
Пускай событие Быть может случиться только при условии появления одного из n попарно несовместимых событий B1, B2, …, Вn,образующих полную группу событий. События
B1, B2, …, Вn,будем именовать догадками для события А. Тогда
Это формула полной возможности.
В действительности, событие Быть может наступить лишь при условии наступления одного из событий B1, B2, …, Вn,т. е.
А = В1А + В2А + … + ВnА,
причем, ввиду несовместимости событий B1, B2, …, Вn,, события B1A, В2А,…, ВnА кроме этого несовместимы. Исходя из этого на основании умножения вероятностей и теорем сложения имеем:
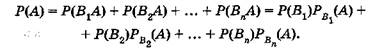
Пример. В магазин для продажи поступает продукция трех фабрик, относительные доли которых имеется: I – 50 %, II – 30 %, III – 20 %. Для продукции фабрик брак соответственно образовывает: I – 2 %, II – 3 %, III – 5 %. Какова возможность того, что изделие данной продукции, случайно купленное в магазине, окажется доброкачественным (событие А)?
Ответ: Вероятны следующие три догадки: Н1, Н2, Н3 – купленная вещь выработана соответственно на I, II, и III фабриках; разумеется, совокупность этих догадок полная, причем их возможности Р(Н1) = 0,5, Р(Н2) = 0,3, Р(Н3) = 0,2.
Соответствующие условные возможности события А равны
РН1(А) = 1 – 0,02 = 0,98, РН2(А) = 1 – 0,03 = 0,97, РН3(А) = 1 – 0,05 = 0,95.
По формуле полной возможности имеем Р(А) = 0,5 • 0,98 + 0,3 • 0,97 + 0,2 • 0,95 = 0,971.
Формула Байеса.
Пускай в условиях рассуждения, относящегося к формуле полной возможности, произведено одно опробование, из-за которого случилось событие А. Спрашивается: как изменились (в связи с тем, что событие А уже случилось) возможности догадок, т. е. величины P(Bk), k = 1, …, n?
Отыщем условную возможность PA(Bk).
По формуле умножения и теореме вероятностей (4) имеем
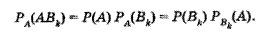Из этого
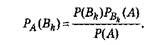
Наконец, применяя формулу полной возможности, находим:
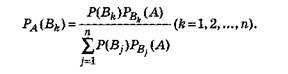
Выше обозначенные формулы именуются формулами Байеса (Томас Байес, либо Бейес, (1702-1761) –британский математик).
Пример. Возможность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) – 0,1. Каждое из орудий создаёт по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова возможность, что успешный выстрел в собственности первому расчету?
Ответ. До опыта вероятны четыре догадки
Н1 = АВ, Н2 = АOВ, Н3 = OАВ, Н4 = OАOВ;
эти догадки образуют полную группу событий.
Возможности их, при свободном действии расчетов, соответственно равны
Р(Н1) = 0,2 • 0,1 = 0,02, Р(Н2) = 0,2 • 0,9, Р(Н3) = 0,8 • 0,1 = 0,08, Р(Н4) = 0,8 • 0,9 = 0,72,
причем Р(Н1) + Р(Н2) + Р(Н3) + Р(Н4) = 1.
Условные возможности для замечаемого события С при данных догадках будут
РН1(С) = 0, РН2(С) = 1, РН3(С) = 1, РН4(С) = 0.
Следовательно, догадки Н1 и Н4 отпадают; а возможности догадок Н2 и Н3 вычисляются по формуле Байеса
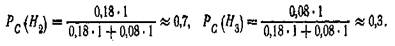
Задание: Установите соответствие между главными понятиями теории вероятностей и теории множеств ((заполните второй столбик).
| Теория множеств | Теория возможностей |
| Множество | |
| Объединение | |
| Пересечение | |
| Непересекающиеся множества | |
| Дополнение | |
| Универсальное множество | |
| Безлюдное множество |
Ответ:
| Теория множеств | Теория возможностей |
| Множество Случайное событие | |
| Объединение | Сумма |
| Пересечение | Произведение |
| Непересекающиеся множества | Несовместные события |
| Дополнение | Противоположное событие |
| Универсальное множество | Точное событие |
| Безлюдное множество | Неосуществимое событие |
Семинарское занятие № 6