Дабы сократить текст m-файла, повторяющиеся команды возможно вынести в отдельный файл и оформить его как функцию, задав её параметры и возвращаемые значения:
function [net,kk,mr]=foo(a,b,X)
[kv,kf]=size(X);
net=som(kf,[a,b]);
Функция делает создание, обучение и обработку результатов обучения сети.
Приступаем к написанию тела функции. Перед созданием сети необходимо выяснить количество входов нейросетевой модели. Оно равняется количеству факторов, т.е. столбцов в массиве X:
[kv,kf]=size(X);
Следующая команда создаёт карту Кохонена net размерностью axb:
net=som(kf,[a,b]);
Где вместо a и b будут продемонстрированы фактические значения.
По окончании перед запуском обучения сети нужно задать его параметры.
Зададим начальные и конечные значения. Все параметры обучения задаются через массив с главных именем options:
options(14)=500; #кол-во эр
options(18)=0.1; #начальная скорость обучения
options(16)=0.01; #конечная скорость обучения
options(17)=0.25*b; #начальный радиус функции соседства
options(15)=1; #конечный радиус функции соседства
Обучение сети net на массиве данных X с заданными параметрами options осуществляется следующей командой:
net=somtrain(net,options,X);
Потом определим номера нейронов победителей Y:
[D2,Y]=somfwd(net,X); # номера нейронов победителей
Первый выходной параметр данной функции D2 – матрица, в которой на пересечении i-й строки и j-го столбца находится квадрат евклидова расстояния между вектором данных i и весовым вектором нейрона j. В будущем изучении данный массив не нужно.
Количество кластеров – количество несовпадающих номеров нейров-победителей в массиве Y. Сами номера возможно взять посредством функции intersect. Эта функция помогает для определения пересечения, она выдаст массив из элементов, каковые принадлежат обоим массивам
NN=intersect(Y,Y); #номера нейронов взявших активацию
kk=length(NN); #количество кластеров
Потом приступаем к расчёту среднего межкластерного расстояния. Это среднее расстояние между центроидами кластеров. В карте самоорганизации центроидами являются весовые векторы нейронов. Возьмём матрицу весовых коэффициентов сети:
W=sompak(net); # матрица весовых коэффициентов
Весовые векторы – строчка матрицы W.
Используем массив с номерами нейронов-победителей, скопируем лишь соответствующие им строки в новую матрицу:
W1=W(NN,:); # массив с номерами нейронов-победителей
Вычислим суммарное векторное расстояние SED и поделим на количество кластеров, дабы выяснить среднее межкластерное расстояние:
SED=0;
for i=1:kk
for j=1:kk
SED=SED+sqrt( sum((W1(i,:)-W1(j,:)).^2));
end
end
mr=SED/kk;
Отбор оптимальной сети.
Нужно выстроить карты самоорганизации с разной размерностью нейронного слоя. Для каждой из карт:
— задать размерность;
— задать параметры обучения;
— совершить обучение на взятом массиве X;
— подсчитать количество кластеров, на каковые поделены исходные 16 столбцов массива Х;
— вычислить среднее межкластерное евклидово расстояние.
Данный метод, с целью сокращения программы, реализуем в виде отдельного файла. Используем двумерную карту самоорганизации. Размеры нейронного слоя обозначим через a и b. В таблице приведены размерности карт.
| A | … | ||||||
| B | … |
По окончании того, как будут выяснены результаты обучения всех карт самоорганизации, среди них необходимо выбрать оптимальную. Оптимальной будем вычислять ту карту, у которой среднее межкластерное евклидово расстояние максимально среди всех карт.
Для отбора оптимальной сети нужно выстроить график.
В совокупности Octave существует пара способов выстроить два графика на одном рисунке, к примеру применять функцию plotyy. В этом случае масштабы по оси ординат будут свободны. Доводы функции: plotyy(X1,Y1,X2,Y2), где массивы X1 и Y1 содержат координаты точки для построения первого графика, X2 и Y2 – второго. Пускай первый график – количество кластеров, второй – межкластерное расстояние. Так как X1 и X2 совпадают, то пригодится организовать 3 массива:
1) Количество нейронов;
2) Количество кластеров;
3) Межкластерное расстояние.
Так, обрисованные выше действия в программе возможно отобразить так:
X(:,deli)=[]; #Удаление
X1=zeros(0,1); # количество нейронов
Y1=zeros(0,1); # количество кластеров
Y2=направляться(0,1); # межкластерное расстояние
for a=3:8
for b=a:a+1
[net,kk,mr]=foo(a,b,X);
X1=cat(1,X1,a*b); #Склейка количества нейронов
Y1=cat(1,Y1,kk); #Склейка количества кластеров
Y2=cat(1,Y2,mr); #Склейка межкластерного расстояния
end
end
plotyy(X1,Y1,X1,Y2); #Построение графика
Выяснить оптимальную сеть возможно по графику:
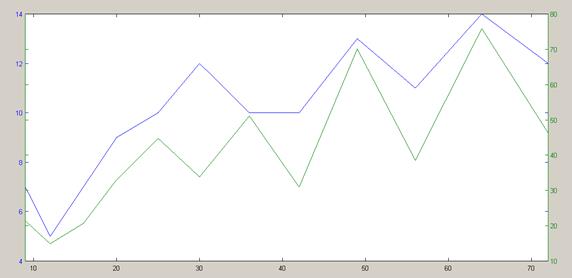
Рисунок 1 – Графики зависимости количества кластеров и межкластерного расстояния от количества нейронов карты.
Тут ось абсцисс – количество нейронов в сети, светло синий линия – количество кластеров, зелёная – среднее межкластерное евклидово расстояние. Как видно, оптимальной есть карта 7х7=49 нейронов, выделившая 13 кластеров.
Вывод: Применяя функционал математического пакета Octave, мы подготовили комплект данных, на которых решалась задача кластеризации. И мы изучили и создали карты самоорганизации – карты Кохонена, с разной размерностью нейронного слоя. Итогом работы стало построение графика зависимости количества кластеров и межкластерного расстояния, благодаря которому мы выяснили оптимальную сеть. Возможно сделать вывод, что оптимальной есть двумерная карта Кохонена 7х7=49 нейронов, выделившая 13 кластеров.