Работа №10
Выполнил: Горх Э.В.
Проверил: Костырко С. А.
2017 год
Цель задачи
Отыскать коэффициент концентрации напряжения, проанализировать внутреннюю сходимость способа, выстроить ответ с точностью до заданного , сравнить полученное в ANSYS ответ с аналитическим. Проанализировать изменение коэффициента концентрации напряжения при трансформации параметров.
Постановка задачи
Разглядим протяженное тело с углублениями по центру сверху и снизу. Тело растягивается вправо и влево с распределенным упрочнением. В силу симметричности задачи возможно разглядывать половинку тела.
Пускай даны физические и геометрические константы:
1) ГПа (модуль Юнга) – плёнки;
2) nu=0,3 (коэффициент Пуассона).
3) d (расстояние между углублениями)
4) r (радиус окружности углубления)
5) t (высота углубления)
6) H = 2 м (ширина и высота тела)
7) (угол)
 a (ширина углубления)
a (ширина углубления)
Ответ задачи (U-shaped)

Рис.1. Модель данной задачи с зафиксированными точками и приложенным упрочнением
1. Выстроена модель (рис.1.), которая складывается из элемента plane182. В качестве модели материала употребляется эластичный изотропный линейный материал, что характеризуют константы E и .
2. Модель до и по окончании деформации:
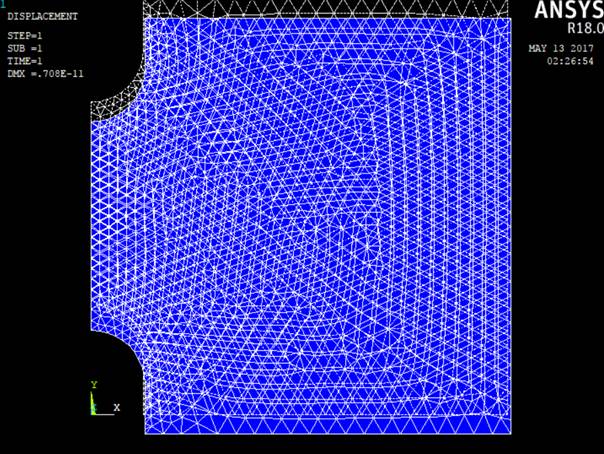
3. Эпюра напряжений по оси Х:
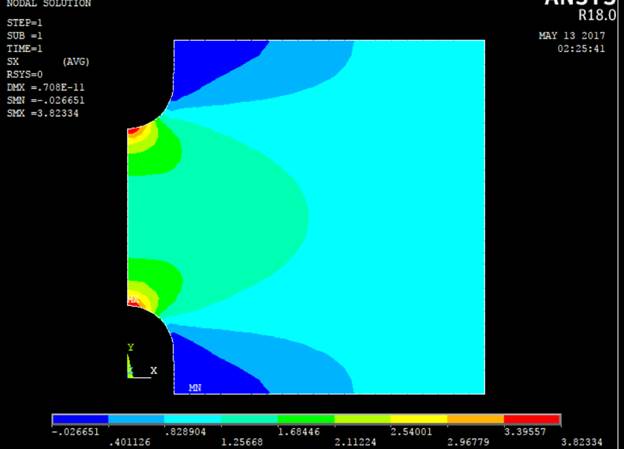
Предстоящие эти будут приведены для H/d = 2
1. Для r/d=0.3 максимально напряжение по оси х будет (при разбиении на 1982 элемента) иметь значение
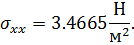
Тогда коэффициент концентрации будет равен, соответственно:
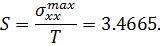
Проверка внутренней сходимости способа по формуле:
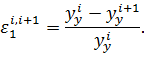
Увеличим разбиение до 2439 элементов. Возьмём
Аналитическое ответ:
2. Для r/d=0.1 максимально напряжение по оси х будет (при разбиении на 1932 элемента) иметь значение
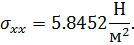
Тогда коэффициент концентрации будет равен, соответственно:
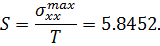
Аналитическое ответ:
Ответ задачи (Semicircular)

Рис.1. Модель данной задачи с зафиксированными точками и приложенным упрочнением
1. Выстроена модель (рис.1.), которая складывается из элемента plane182. В качестве модели материала употребляется эластичный изотропный линейный материал, что характеризуют константы E и .
2. Модель до и по окончании деформации:
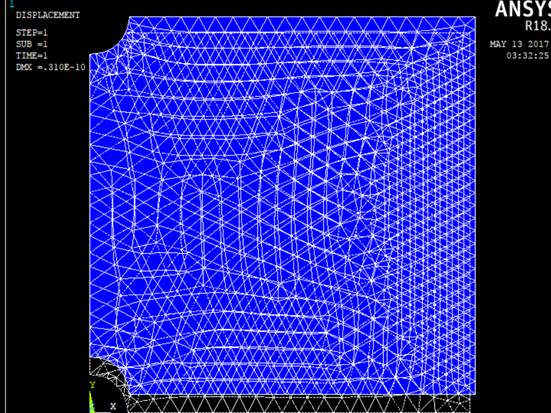
3. Эпюра напряжений по оси Х:
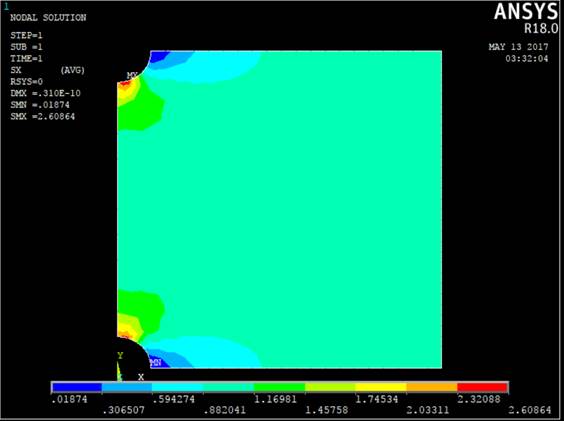
Предстоящие эти будут приведены для H = 2
4. Для 2r/H=0.2 максимально напряжение по оси х будет (при разбиении на 1040 элементов) иметь значение
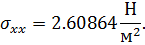
Тогда коэффициент концентрации будет равен, соответственно:
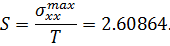
Проверка внутренней сходимости способа по формуле:
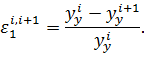
Увеличим разбиение до 1302 элементов. Возьмём
Аналитическое ответ:
5. Для 2r/H=0.8 максимально напряжение по оси х будет (при разбиении на 1932 элемента) иметь значение
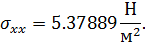
Тогда коэффициент концентрации будет равен, соответственно:
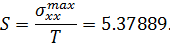
Аналитическое ответ:
Ответ задачи (V-shaped)

Рис.1. Модель данной задачи с зафиксированными точками и приложенным упрочнением
1. Выстроена модель (рис.1.), которая складывается из элемента plane182. В качестве модели материала употребляется эластичный изотропный линейный материал, что характеризуют константы E и .
2. Модель до и по окончании деформации:
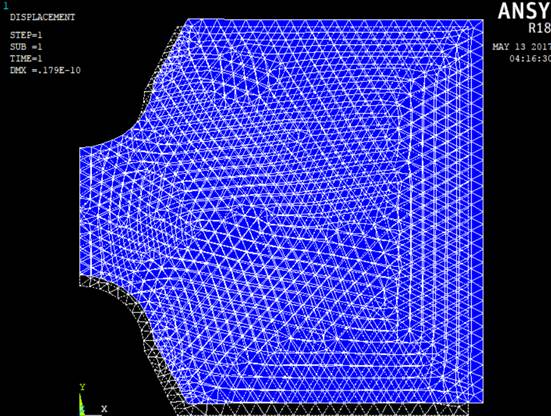
3. Эпюра напряжений по оси Х:
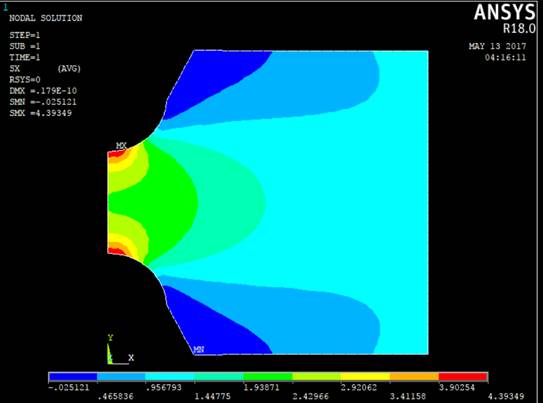
Предстоящие эти будут приведены для H = 2
4. Для максимально напряжение по оси х будет (при разбиении на 1890 элементов) иметь значение
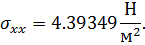
Тогда коэффициент концентрации будет равен, соответственно:
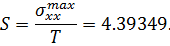
Проверка внутренней сходимости способа по формуле:
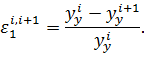
Увеличим разбиение до 2452 элементов. Возьмём
Аналитическое ответ:
5. Для максимально напряжение по оси х будет (при разбиении на 1932 элемента) иметь значение
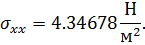
Тогда коэффициент концентрации будет равен, соответственно:
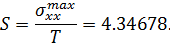
Аналитическое ответ: