Этот способ пребывает в последовательном улучшении опорного замысла перевозок методом отыскания на каждом шаге удачных циклов переноса грузов. Опорный замысел для данного способа (как и для других способов ответа транспортной задачи способом потенциалов) возможно организовать, используя способ «северо-западного» угла.
Более детально разглядим сейчас процесс формирования очередного цикла переноса на каждом новом шаге метода.
Разумеется, что при перемещении х единиц груза по некоему циклу с ценой g цена перевозок изменяется на величину х?g.
Тогда, для улучшения текущего замысла перевозок имеет суть перемещать перевозки лишь по тем циклам, цена которых отрицательна.
В случае, если циклов с отрицательной ценой в таблице больше не осталось, это указывает, что оптимальный замысел достигнут.
При улучшении замысла циклическими переносами пользуются приемом, заимствованным из симплекс-способа: на каждом шаге (цикле) заменяют одну свободную переменную на базовую, т.е. заполняют одну клетку и вместо того освобождают одну из базовых клеток.
Возможно доказать, что для любой свободной клетки транспортной таблицы постоянно существует цикл (и притом единственный), одна из вершин которого лежит в данной клетке, а все остальные в базовых клетках. В случае, если цена для того чтобы цикла, с плюсом в свободной клетке, отрицательна, то замысел возможно улучшить. Количество единиц груза (х), каковые возможно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла.
Пример 1. Распределительный способ ответа транспортной задачи.
Отыскать оптимальный замысел перевозок транспортной задачи, имеющей следующую таблицу издержек:
| Сток Исток | Запасы: | ||||||||
| Заявки: |
Ответ:
Способом «северо-западного» угла отыщем опорный замысел перевозок:
| Сток Исток | Запасы: | ||||||||
| Заявки: |
1. Составленный посредством способа «северо-западного угла» опорный замысел имеет шесть базовых клеток в соответствующей ему транспортной таблице, что разрешает его применять без модификаций для предстоящего ответа задачи.
r = n + m – 1 = 4 + 3 – 1 = 6
Посчитаем сейчас цена отысканного опорного замысла:
L = 22?10 + 9?7 + … = 796
Постараемся улучшить отысканный опорный замысел перевозок способом циклических переносов.
2. Вычислим цену цикла для каждой свободной клетки. Количество свободных клеток в транспортной таблице данного опорного замысла равняется: k = 3?2 = 6.

3. Для всех свободных переменных (клеток) с отрицательной ценой цикла вычислим предельное число груза, которое возможно перенести по соответствующему циклу. Разумеется, что предельное число груза, которое возможно переместить по некоему выбранному циклу будет равняется минимальному значению груза среди отрицательных клеток цикла.
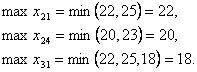
4. Сейчас для всех свободных переменных с отрицательной ценой циклов вычислим чёрта . Полученные значения будем применять при выборе конкретного цикла пересчета на данной итерации метода.
| ij | 2,1 | 2,4 | |
| g | — 4 | — 2 | — 2 |
| x | |||
| gx | — 88 | — 40 | — 36 |
5. Выберем ту свободную переменную, которой соответствует мельчайшее значение величины и перенесем единиц груза по циклу, соответствующему выбранной переменной: (ij) = (2,1); g21 = — 4; .
| Сток Исток | Запасы: | ||||||||
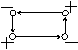 |
|||||||||
| Заявки: |
Так, мы уменьшим значение целевой функции L – цена замысла перевозок – на 88 единиц. Новому улучшенному замыслу перевозок будет соответствовать следующая таблица перевозок:
| Сток Исток | Запасы: | ||||||||
| Заявки: |
Полученный на этапе 5 первой итерации метода новый замысел перевозок имеет шесть базовых клеток в соответствующей ему транспортной таблице (см. таблицу выше), что разрешает его применять без модификаций для предстоящего ответа задачи.
r = 6
Цена отысканного замысла перевозок равна:
L = 31?7 + 22?5 + … = 708
Постараемся снова улучшить отысканный опорный замысел перевозок. Для этого перейдем к пункту 2 метода:
2. Вычислим цену цикла для каждой свободной переменной:

3. Вычислим предельное число груза, которое возможно перенести по циклу с отрицательной ценой. Результаты расчетов, проделанных в прошлом пункте, продемонстрировали, что эта таблица содержит всего одну переменную и соответствующую ей свободную клетку. Так, на данной итерации метода нет необходимости в выборе цикла переноса.
.
4. Для единственной свободной переменной вычислим значение критерия :
.
| Сток Исток | Запасы: | ||||||||
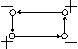 |
|||||||||
| Заявки: |
Перенесем единиц груза по циклу
(2,4)+, (3,4)-, (3,3)+, (2,3)-, уменьшив этим значение целевой функции на 40 единиц. Новому улучшенному замыслу перевозок будет соответствовать следующая таблица перевозок:
| Сток Исток | Запасы: | ||||||||
| Заявки: |
Полученный на этапе 5 первой итерации метода новый замысел перевозок имеет шесть базовых клеток в соответствующей ему транспортной таблице (см. таблицу выше), что разрешает его применять без модификаций для предстоящего ответа задачи.
r = 6
Цена отысканного замысла перевозок равна:
L = 31?7 + 22?5 + … = 668
Постараемся снова улучшить отысканный опорный замысел перевозок. Для этого перейдем к пункту 2 метода:
2. Вычислим цену цикла для каждой свободной переменной:
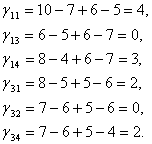
3. Так как не существует циклов свободных переменных с отрицательной ценой, полученный замысел перевозок есть оптимальным. Цена оптимального замысла перевозок, как было посчитано ранее, образовывает 668 единиц.
Разглядим еще один пример ответа хорошей транспортной задачи способом циклических переносов. В следующем примере мы разглядим такую транспортную задачу, использование к которой способа «северо-западного» угла для нахождения опорного замысла даст вырожденный опорный замысел. Так, данный пример проиллюстрирует ответ транспортной задачи с вырожденным замыслом перевозок.
Пример 2. Ответ транспортной задачи.
Отыскать оптимальный замысел перевозок транспортной задачи, имеющей следующую таблицу издержек:
| Сток Исток | Запасы: | ||||||
| Заявки: |
Ответ:
1. Способом «северо-западного» угла отыщем опорный замысел перевозок:
| Сток Исток | Запасы: | ||||||
| Заявки: |
Полученный опорный замысел перевозок имеет четыре базовых клетки в соответствующей ему транспортной таблице (см. таблицу выше), что не разрешает применять его напрямую без модификаций для предстоящего ответа задачи.
r = n + m – 1 = 3 + 3 – 1 = 5 ¹ 4
Замысел получается вырожденный.
| Сток Исток | Запасы: | ||||||
| 40-e | |||||||
| e | |||||||
| 20+e | |||||||
| 20-e | |||||||
| Заявки: |
Дабы избежать этого, нарушаем баланс заявок и запасов на e в 1 и 3 строчках, не нарушая неспециализированного баланса. Сейчас:
r = 5,
а отысканный опорный замысел возможно применять в будущем для ответа задачи.
Цена отысканного замысла перевозок равна:
L = 20?10 + 20?5 + 23?5 + 20?6 = 535.
Постараемся улучшить отысканный опорный замысел перевозок способом циклических переносов.
2. Вычислим цену цикла для k = 4 свободных клеток.
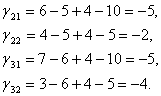
3. Вычислим предельное число груза, которое возможно перенести по циклам с отрицательной ценой.

4. Для свободных переменных с отрицательной ценой цикла вычислим чёрта .
| (i,j) | 2,1 | 2,2 | 3,1 | 3,2 |
| g | — 5 | — 2 | — 5 | — 4 |
| g?max x | — 100 | — 40 | — 100 | — 80 |
5. Перенесем max x21 = 20 единиц груза по циклу свободной переменной х21, уменьшив значение целевой функции на 100 единиц, другими словами:
| Сток Исток | Запасы: | ||||||
 |
40-e | ||||||
| e | |||||||
| 20+e | |||||||
| 20-e | |||||||
| Заявки: |
В следствии возьмём следующий (уже не вырожденный) замысел перевозок:
| Сток Исток | Запасы: | ||||||
| 40-e | |||||||
| 20+e | |||||||
| 20+e | |||||||
| 20-e | |||||||
| Заявки: |
Полученный на этапе 5 первой итерации метода новый замысел перевозок имеет пять базовых клеток в соответствующей ему транспортной таблице (см. таблицу выше), что разрешает его применять для предстоящего ответа задачи.
r = 5
Цена отысканного замысла перевозок равна:
L = 20?5 + 20?4 + 20?6 + 3?5 + 20?6 = 435
Постараемся еще улучшить отысканный опорный замысел перевозок. Для этого перейдем к пункту 2 метода:
2. Вычислим цену цикла для каждой свободной переменной.
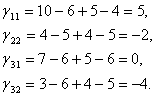
3. Предельное число груза, которое возможно перенести по циклу свободной переменной х32 = 20.
4. g32?max x32 = — 80.
| Сток Исток | Запасы: | ||||||
 |
40-e | ||||||
| 20+e | |||||||
| 20+e | |||||||
| 20-e | |||||||
| Заявки: |
5. Перенесем 20 единиц груза по циклу переменной x32, , уменьшив значение целевой функции на 80 единиц.
В следствии возьмём следующий замысел перевозок:
| Сток Исток | Запасы: | ||||||
| 40-e | |||||||
| 40+e | |||||||
| 20+e | |||||||
| e | |||||||
| Заявки: |
Полученный на этом этапе новый замысел перевозок имеет пять базовых клеток в соответствующей ему транспортной таблице (см. таблицу выше).
r = 5
Цена отысканного замысла перевозок равна:
L = 40?4 + 20?6 + 3?5 + 20?3 = 355
Еще раз постараемся улучшить отысканный опорный замысел перевозок. Для этого перейдем к пункту 2 метода:
2. Вычислим цену цикла для каждой свободной переменной.
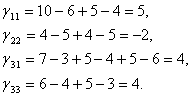
3. Предельное число груза, которое возможно перенести по циклу единственной свободной переменной х22, имеющей отрицательную цену цикла, равняется вечно малой величине e. Полагая e = 0, возьмём окончательный оптимальный замысел перевозок:
4.
| Сток Исток | Запасы: | ||||||
| Заявки: |
цена которого равна:
L = 40?4 + 20?6+ 3?5 +20?3 =355
Примененный способ «ликвидации вырождения» методом трансформаций запасов на бесконечно малую величину e не всегда эргономичен, поскольку требует дополнительных действий с вечно малыми размерами e. Существенно проще было бы не изменять запасы, а вместо величины e поставить в базовой клетке нуль. Тогда базовая клетка будет тем различаться от свободной, что в ней нуль поставлен, а в свободной нет.
Предстоящие манипуляции с транспортной таблицей будут аналогичны тем, каковые мы осуществляли в обстановках, в то время, когда в базовых клетках находились лишь хорошие перевозки. Отличие состоит лишь в том, что в то время, когда одна из отрицательных вершин цикла окажется в базовой клетке с нулевой перевозкой, необходимо переносить по этому циклу нулевую перевозку. Таковой перенос нулевой перевозки стал называться фиктивный перенос.
Разглядим сейчас второй способ ответа транспортной задачи – способ потенциалов.
