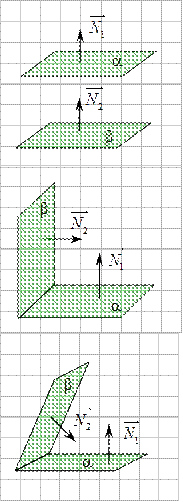
Разглядим частные случаи размещения плоскости , определяемой неспециализированным уравнением: .
1. В случае, если ,то .
, то .
В случае, если , то .
В случае, если , то проходит через начало координат.
2. В случае, если , то .
В случае, если , то .
В случае, если , то .
3. В случае, если , то проходит через ось .
В случае, если , то проходит через ось .
В случае, если , то проходит через ось .
4. В случае, если – это уравнение плоскости .
В случае, если – это уравнение плоскости .
В случае, если – это уравнение плоскости .
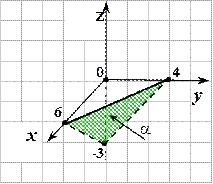 5. В случае, если , то уравнение плоскости возможно привести к виду:
5. В случае, если , то уравнение плоскости возможно привести к виду: 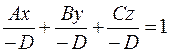 либо
либо 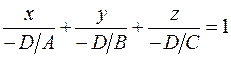 . Обозначив
. Обозначив 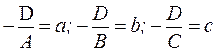 ,
,
возьмём 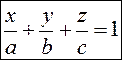 (3) – уравнение плоскости в отрезках на осях,
(3) – уравнение плоскости в отрезках на осях,
где , , – точки пересечения с осями координат.
Типовые примеры. Выстроить плоскости, заданные неспециализированными уравнениями:
1.
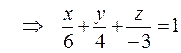 .
.
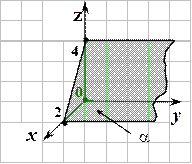
2.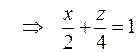 . . 
|
3.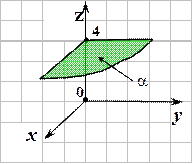 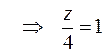 . . |
4.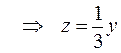 . . 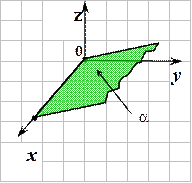
|
5. . 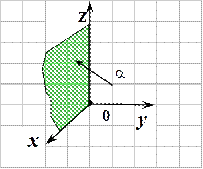
|
 3. Уравнение плоскости, проходящей через три точки
3. Уравнение плоскости, проходящей через три точки
Пускай даны точки , , принадлежащие плоскости .
Точка — произвольная точка плоскости . Выстроим векторы: ,
,
.
Так как точки лежат в одной плоскости, то векторы компланарны. Следовательно, их смешанное произведение равняется нулю.
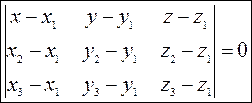 (4) (4) |
— уравнение плоскости, проходящей через три точки. |
Типовой пример.Составить уравнение плоскости , проходящей через точки , , .
Пускай — текущая точка плоскости , следовательно, , векторы , соответственно их смешанное произведение равняется нулю: .
, , .
Смешанное произведение этих векторов в координатной форме
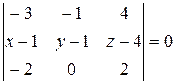 .
.
, раскрыв скобки и приведя подобные члены, приобретаем уравнение плоскости : — неспециализированное уравнение плоскости, 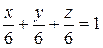 – уравнение плоскости в отрезках на осях.
– уравнение плоскости в отрезках на осях.
Типовой пример.Составить уравнение плоскости, проходящей через точки , , .
Используем уравнение (4):
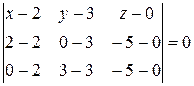
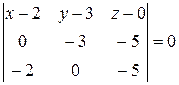
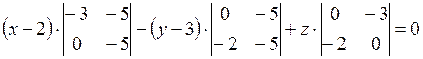
.
Пучок плоскостей
Пускай плоскости и пересекаются по прямой a.
Плоскости, проходящие через линию пересечения двух плоскостей, образуют пучок плоскостей. Уравнение пучка плоскостей: .
 Дабы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.
Дабы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.
Типовой пример. Написать уравнение плоскости , проходящей через линию пересечения плоскостей и , и через точку .
Запишем уравнение пучка плоскостей: .
 Значение определяем из условия, что плоскость проходит через точку : , либо
Значение определяем из условия, что плоскость проходит через точку : , либо 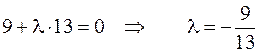 .
.
Следовательно, искомое уравнение имеет форму:
Обоюдное размещение плоскостей. Расстояние от точки до плоскости
, где ,
, где .
6.1. В случае, если
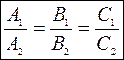 – условие параллельности плоскостей.
– условие параллельности плоскостей.
6.2. В случае, если
 – условие
– условие
перпендикулярности
плоскостей.
6.3. В случае, если , то 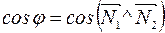
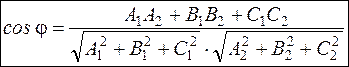 .
.
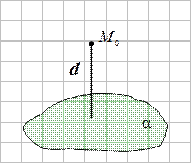
7. Расстояние от точки до плоскости
находим по формуле 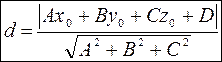
Типовой пример. Составьте уравнение плоскости, проходящей через точки А(1; 2; 21), В(2; 1; 1) перпендикулярно плоскости .
Пускай – обычный вектор данной плоскости. Потому, что искомая плоскость проходит через точки А и В и перпендикулярна данной плоскости, то векторы и параллельны искомой плоскости. Значит, обычный вектор искомой плоскости возможно отыскать как векторное произведение векторов и .
, ,
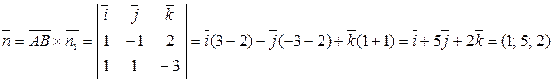 .
.
Уравнение искомой плоскости запишется в виде
, либо .
Типовой пример. Отыскать уравнение плоскости , проходящей через точку , параллельно плоскости : .
, значит, нормаль плоскости будет нормалью плоскости . Нормаль плоскости , значит . Пускай — текущая точка плоскости . Тогда вектор .  , следовательно, их скалярное произведение ,т.е. , либо , либо .
, следовательно, их скалярное произведение ,т.е. , либо , либо .
Прямая в пространстве
Неспециализированные уравнения прямой
Прямая возможно задана как линия пересечения двух плоскостей.

|
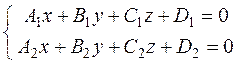
|
(1) – неспециализированные уравнения прямой . |
2.Канонические уравнения прямой
Пускай заданы прямая , вектор и точка  .
.
Произвольная точка лежит на прямой , в случае, если
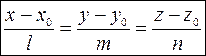 (2) –канонические уравнения прямой .
(2) –канонические уравнения прямой .
3десь: – текущие координаты, — координаты точки , – координаты вектора .
Типовой пример. Привести неспециализированные уравнения прямой к каноническому виду.
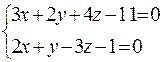 .
.
1-й метод. 1) Отыщем точку , принадлежащую прямой .
Предположим, что и решим совокупность
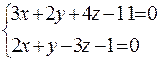 ,
, 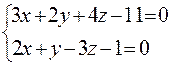 .
.
2) Отыщем вектор , параллельный прямой . Так как он должен быть перпендикулярен векторам и , то за возможно принять векторное произведение векторов и .
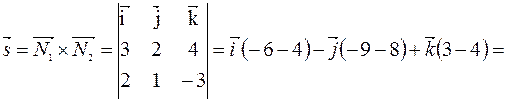
, где .
Искомая прямая определяется уравнениями 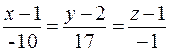 .
.
2-й метод. Отыщем две искомой прямой и точки.
Предположим, что и решим совокупность
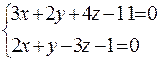 ,
, 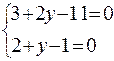 .
.
( см. 1 метод ответа).
Записываем уравнения прямой , проходящей через точки и
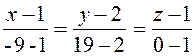
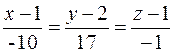 .
.
Типовой пример. Написать канонические и параметрические уравнения прямой , проходящей через точку , параллельной оси ОУ.
Так как искомая прямая параллельна оси ОУ, то в качестве ее направляющего вектора возможно забрать вектор (тут данный вектор возможно разглядывать как направляющий вектор оси ОУ).
Приобретаем уравнения прямой :
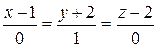 – канонические;
– канонические;
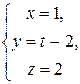 – параметрические.
– параметрические.
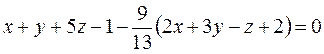 либо
либо