Разглядим действие нерегулярного беспокойства на примере бортовой качки, но все рассуждения будут иметь значение и для других видов качки.
Главная задача — выяснить спектр качки S????. Для этого используем известную из направлений по автоматическому управлению теорему А. Я. Хинчина об определении спектральной плотности выходного процесса в колебательной совокупности:
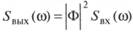(5.125)
где Ф(со)— модуль передаточной функции.
В качестве входного процесса при качке помогает беспокойство, спектральная плотность которого Sr???, а в качестве выходного процесса — качка, спектральная плотность которой S????. Задача пребывает в определении модуля передаточной функции. В отечественных обозначениях теорему Хинчина возможно записать в виде
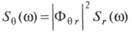(5.126) По формулам (5.113) либо (5.115) можем выяснить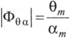 
В случае, если отыскать в памяти, что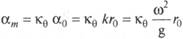 
, то формулу
для Фqa возможно преобразовать
(5.127)
Из этого
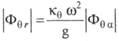(5.128) и тогда
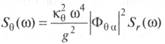
либо
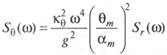(5.129)
Зная S????, можем выяснить дисперсию бортовой качки
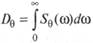(5.130) и амплитуды бортовой качки
¦ 
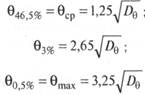(5.131)
Подобным образом возможно определять амплитуды вторых видов качки, перемещений и ускорений заданных точек на установке, что особенно принципиально важно при ответе вопросов, которые связаны с заливаемостью.
О возможности работы ППБУ при разной погоде возможно делать выводы, выстроив зависимость ?mах = ?0,5% от балльности беспокойства и сравнив ее с предельным из условий работы бурового оборудования либо буксирной совокупности углом наклонения, к примеру, 3° (рис. 5.33). Наглядно видно, что установка может бурить либо буксироваться на беспокойстве до 6 баллов.
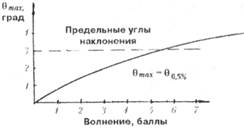Рис. 5.33. Ограничения ра боты ППБУ по балльности
Еще в ходе проектирования возможно отрабатывать форму плавучей установки так, дабы уменьшить качку, т. е. сократить количество простоев по гидрометеорологическим обстоятельствам и значительно повысить экономичность буровых работ.
Совокупности позиционирования полупогружных буровых
Установок
В совсем независимую задачу вырастает неприятность удержания ПБУ полупогружного типа над точкой работы. Сейчас кроме того говорят о появлении нового мореходного качества — позиционирования, т. е. способности плавающего сооружения удерживаться над точкой работы так, дабы перемещения в горизонтальной плоскости (на поверхности воды) не превышали заданных пределов (в большинстве случаев 4—5 % глубины моря в месте работы).
Наряду с этим совокупности позиционирования смогут быть или пассивными (якорные, тросовые совокупности и т. д.), или активными (динамическое позиционирование посредством подруливающих устройств разного типа). Практически же позиционирование — это управляемость на месте, исходя из этого она рассматривается в рамках неспециализированной управляемости плавучих объектов.
Задачей совокупности позиционирования любого типа есть противодействие внешним упрочнениям и удержание буровой установки над устьем скважины в пределах допускаемых отклонений. Для этих целей допустимо применять якорную совокупность, совокупность динамического позиционирования либо их комбинации.
В якорной совокупности для упрочнений, нужных для удержания ППБУ, используются уложенные на дно акватории якоря. Передача упрочнений между установкой и якорями осуществляется через якорные цепи. При громадных длинах якорных цепей перемещения ППБУ под внешним действием смогут стать больше допустимых, исходя из этого на использование якорных совокупностей существует ограничение по глубине (150-200 м) .
В совокупностях динамического позиционирования силы удержания создаются разного рода движителями (винто-рулевые колонки, крыльчатые движители, подруливающие устройства тоннельного типа и т. д.) , работа которых координируется так, дабы в любой момент времени создать суммарное упрочнение нужной величины, противодействующее внешнему упрочнению. Работоспособность таковой совокупности
меньше зависит от глубины акватории, но из-за некоей инерционности ее использование на малых глубинах затруднено.
В состав совокупности динамического позиционирования кроме дви-жительных комплексов входят сложные и дорогие совокупности автоматического управления и приводы, исходя из этого ее цена приближается к цене всей ППБУ. На данный момент осваиваются глубины по большей части до 200 м, исходя из этого самый распространены якорные совокупности как достаточно простые и действенные средства удержания.
Разные схемы заякорения ППБУ отличаются друг от друга расположением и количеством якорных линий. Для ППБУ с очевидно выраженной симметрией довольно ДП и мидель-шпангоута характерно использование рассредоточенных схем, каковые одинаково отлично принимают внешние упрочнения с любого направления, но время от времени используются и ориентированные схемы, рассчитанные на восприятие внешних упрочнений, действующих в каком-либо конкретном (в большинстве случаев преимущественном) направлении.
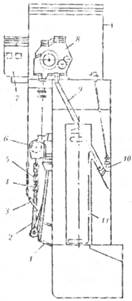
Комплект элементов, входящих
в состав каждой якорной линии,
продемонстрирован на рис. 5.34 при походном
положении устройства. На буровых
установках употребляются якоря со
временных конструкций, владею
щие коэффициентом держащей
силы (отношением предельной
силы удержания к весу самого яко
ря) около 20—23. Цепи должны
Рис. 5.34. Схема расположе- быть очень большой прочности,
ния оборудования якорной Нижняя и верхняя звездочки вы-
линии совокупности позициониро- полняют те же функции, что и на-
вания
1 — кронштейн якорный; правляющие шкивы в тросовых си-
2 — якорь; 3 — устройство подры- стемах. Якорные линии в большинстве случаев
ва якоря; 4 — вертлюг; 5 — якор- размещаются парами, что разрешив-
иая цепь; в — нижняя направляю- ет применять в качестве якорных
щая; 7 — пост управления якорной
лебедкой; 8 — якорная лебедка; механизмов брашпили. Цепные
9 — цепной клюз; 10 — устройство коробки, в большинстве случаев, размещаются
отдачи цепи; 11 — цепной ящик в стабилизирующих колоннах.
Раскладку якорей около буровой установки по заблаговременно определенной схеме снабжают особые суда — завозчики якорей. Для обеспечения возможности исполнения данной операции в любую секунду времени в состав каждой линии входят или буй с буйрепом, или бе-гунковая снасть, которая по окончании завозки якоря возвращается на установку. Длину каждой якорной линии выбирают из условия, дабы некая ее часть, находящаяся конкретно у якоря, оставалась лежащей на грунте при действии на установку упрочнений во всем разглядываемом диапазоне внешнего действия. При исполнении этих условий якорь снабжает большую держащую силу. Такие якорные линии принято именовать долгими.
По окончании раскладки якорей во всех якорных линиях создается некое предварительное натяжение. В случае, если условно вычислять, что якорные линии противоположных бортов симметричны, то значения начальных натяжений в них должны быть однообразными. Любое смещение установки из положения равновесия ведет к перераспределению упрочнений в якорных линиях (рис. 5.35). Векторная сумма горизонтальных направляющих натяжений во всех якорных линиях должна быть равной по величине и противоположно направленной внешнему упрочнению, вызывающему смещение установки.
Рис- 5-35. Перераспределение уси-
лий в якорных линиях при сме
щении установки под действием
внешних силJ
Это, само собой разумеется, абсолютно справедливо при статическом внешнем действии (неизменно дующий ветер, течение). Но в настоящих условиях картина пара сложнее, поскольку на установку действуют волны, переменные составляющие в ветре и т. д. В большинстве случаев используется принцип разделения перемещений от осреднен-ных, фактически постоянных волновых нагрузок (силы волнового дрейфа), и от периодических, вызывающих качку. В первом случае решается чисто статическая задача, определяется равновесное положение, а после этого рассматриваются колебания ППБУ довольно смещенного положения.
Конкретно для этого положения определяются коэффициенты жесткости, входящие в уравнения качки, как мы это проиллюстрировали в п. 5.2.3.5.
Зак.724 209
Настоящий раздел посвящен ответу статической задачи. В общем случае внешним упрочнениям противодействуют, правда в различной мере, все якорные линии. Степень участия каждой из них при всех других равных условиях (глубина акватории, протяженность якорной цепи и т. д.) зависит от угла между проекцией якорной линии на горизонтальную плоскость и направлением внешнего действия.
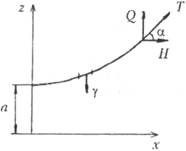
Сначала разглядим связь между формой провисающей части цепи и натяжением для раздельно забранной якорной связи. Уравнение весомой якорной линии возможно записано в виде (рис. 5.35)
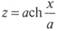(5.132)
где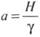 
, Н — горизонтальная составляющая упрочнения в цепи (рас-
пор), ? = gq, g = 9,81 м/с2, q — погонная масса цепи, кг/м; х — текущее значение координат.
Изюминкой цепной линии есть равенство распоров во всех ее точках. Упрочнение в точке цепи с ординатой z , действующее по касательной к участку цепи, будет равняется Т = ?z, протяженность цепи S до данной же точки от точки пересечения цепной линии с осью ординат (в данной точке dz/dx=0)
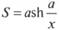(5.133)
Для любой точки цепной линии честны очевидные формулы
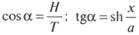(5.134)
Эффективность якорной совокупности позиционирования возможно оценить, разглядев отклонение буровой установки от устья скважины и сравнив величину суммарного упрочнения, создаваемого всеми якорными линиями, с тем внешним действием, которое стало причиной смещение буровой установки от положения равновесия. Нахождение буровой установки на точке бурения допустимо в трех режимах: рабочем (беспокойство до 6 баллов), штормового отстоя (до 8 баллов) и выживания (9 баллов). В инструкции по эксплуатации указаны предельно допустимые отклонения установки от устья скважины и требуемый запас прочности цепей для каждого из этих режимов (табл. 5.1).
Как видим, проектирование якорной совокупности позиционирования в конечном итоге сводится к определению разрывного упрочнения цепи, ее предварительного натяжения и длины.
| Таблица 5.1 | ||
| допустимые запаса | ||
| отклонения и Коэффициенты прочности ППБУ от устья | ||
| скважины | ||
| Допустимое от- | Запас | |
| Режим эксплуатации | клонение ППБУ, % от глу- бины | прочности якорной цепи |
| Рабочий | ||
| режим Штормовой отстой Выживание | 8 15 | 2 1,2 |
Разглядим вероятный порядок определения этих параметров. Потому, что задача имеет нелинейный темперамент, используем способ последовательных приближений, что легко реализовать на компьютере.
В первом приближении калибр цепи, а следовательно, и ее разрывное упрочнение принимают по близкому прототипу либо по предварительным приближенным расчетам, время от времени по эксплуатации и опыту проектирования. На основании выбранных черт с применением действующих на цепи стандартов определяют погонную массу цепи q. Исходя из значе-
ния Hmах, соответствующего максимально допустимому натяжению в режиме ожесточённого шторма, отыщем требуемую длину якорной цепи:
(5.135)
где
протяженность проекции цепи длиной Smах на ось Ох; ? — глубина акватории в месте работы ППБУ;
Для лучшего представления жесткостной характеристики якорной цепи разглядим условное исходное положение, при котором участок цепи, равный по длине глубине акватории, расположен вертикально, а другая часть лежит на грунте. В этом случае распор H и проекция провисающего участка цепи ?равны нулю (рис. 5.36).
| Рис. 5.36. Форма цепной линии |
Из этого положения будем перемещать верхнюю точку цепи, которая именуется клюзовой, увеличивая значение распора с некоторым
заданным наперед шагом в диапазоне от H=0 до Н = Hmах. Схема трансформации формы провисания при повышении распора от Нi до Hi+1 продемонстрирована на рис. 5.37. Наряду с этим протяженность участка цепи, что поднимается над грунтом, образовывает
(5.136) Одновременно с этим смещение клюзовой точки равняется
(5.137)
С учетом участка цепи _?i+1, лежащего на грунте, изменение длины проекции всей цепи
(5.138)
Так, для каждого значения Н возможно отыскать соответствующее значение длины проекции _? (а следовательно, и положение клюзовой точки), т. е. выстроить зависимость Н = ?(_?) (рис. 5.38).
Чтобы выяснить требуемое предварительное натяжение примем в качестве базисного режим бурения. Нанесем на кривую
точку а,в которой распор равен . Абсцисса b соот-
ветствует большому смещению ППБУ от скважины. Принимая максимально допустимое значение смещения bc = 0,04?, возьмём на кривой точку d, соответствующую предварительному натяжению Т0.
Рис. 5.37. Изменение формы про- Рис. 5.38. Форма зависимости
висания цепи при трансформации рас- Н = ?(_?)
пора
Итак, для заданного в первом приближении калибра цепи найдены значения длины и предварительного натяжения. Эти характеристики должны быть выдержаны в ходе раскладки во всех якорных цепях совокупности позиционирования.
Для оценки правильности выбора параметров якорной совокупности нужно вычислить суммарное упрочнение, создаваемое всеми якорными линиями при смещении буровой установки от устья скважины, — восстанавливающее упрочнение. Рекомендуется разглядеть смещение на протяжении каждой из якорных линий, на протяжении осей симметрии и на протяжении некоторых характерных линий. Для прямоугольной в плане ППБУ таковой линией будет, к примеру, ее диагональ. При симметричном размещении якорей возможно ограничиться анализом направлений смещения в рамках одного квадранта.
В сформулированной так задаче для вычисления относительного перемещения клюзовой точки каждой якорной линии можно считать известными направление и величину смещения. Связанное с этим изменение длины проекции якорной линии (рис. 5.39)
(5.139)
где — длины проекций всей якорной цепи на горизонталь-
ную плоскость до и по окончании смещения соответственно; r — расстояние, на которое переместилась клюзовая точка.
Для отысканного так значения _??посредством кривой H = ?(_?) определяют новое значение натяжения.
Восстанавливающее упрочнение, создаваемое якорной совокупностью позиционирования, равняется векторной сумме значений распора во всех линиях. Его нужно сравнить с величиной внешнего действия,
позвавшего отклонения ППБУ от
устья скважины. Расчет восстанав
ливающего упрочнения делают для
трех режимов эксплуатации установ
ки, разглядывая, с одной стороны,
максимально допустимое смещение,
а с другой, — самый неблагопри
ятное сочетание внешних воздей
ствий предельной для выбранного
режима интенсивности.
Рис. 5.39. К определению длины На базе результатов сравне-
проекции якорной линии ния упрочнений от внешнего воздей-
ствия и восстанавливающих упрочнений для всех режимов вносят в данные, принятые в первом приближении, нужные коррективы. Расчет повторяют до получения нужной степени соответствия.
направляться иметь в виду, что режимы ежегодного и жестокого «шторма» появляются существенно реже, чем режим бурения, исходя из этого для удержания значений отклонения буровой установки от натяжения и устья скважины в цепях в допустимых пределах довольно часто маневрируют цепями. Он содержится в заблаговременном целенаправленном выбирании цепей наветренного борта либо травлении цепей подветренного. Предложенный выше порядок расчета возможно использован и для обоснования схем для того чтобы маневрирования.
Динамические совокупности позиционирования устанавливают в основном на самоходных ППБУ. Разглядим более детально два самые употребительных варианта: с подруливающими устройствами тоннельного типа (винт в трубе) и винто-рулевые крыльчатые движители и поворотные колонки.
Главные расчетные маневры для ППБУ — это или удержание ее от дрейфа при самоё неблагоприятном направлении внешних действий максимальной интенсивности, или перевод ее в положение, при котором внешнему действию по большей части противодействуют главные движители. Во втором случае нужно дополнительно учитывать сопротивление воды повороту установки.
Расчетная схема для установки с подруливающими устройствами тоннельного типа продемонстрирована на рис. 5.40 на примере ППБУ с двумя понтонами. Уравнения равновесия проекций действующих сил на оси Ох и Оу и уравнение моментов в совокупности координат, начало которой сходится с центром тяжести ППБУ, ось Ох направлена в шнобель на протяжении ДП, ось Оу — на правый борт, имеют следующий вид:
(5.140)
(5.141) 215
Рис. 5.40. Схема упрочнений, действующих на ППБУ с подруливающими устройствами тоннельного типа
(5.142)
где ха, уа — координаты точки приложения результирующей аэродинамического действия; _?— угол между диаметральной плоскостью и направлением ветра; vw — скорость ветра; vs — скорость течения; Q — площадь парусности надводной части буровой установки; xh yh ~ координаты точки приложения результирующей сил сопротивления обтеканию корпуса ППБУ потоком воды; ?— угол между скоростью течения и ДП установки; ? — площадь намоченной поверхности загружённой части ППБУ; Са, Ch ~ безразмерные коэффициенты аэродинамической и гидродинамической сил соответственно; ?1 — массовая плотность воздуха; ? — массовая плотность воды; ?х, ?у — безразмерные коэффициенты подъёмной силы и сопротивления руля; S — площадь руля; r — отстояние центра гидродинамического давления от ДП понтона на руле в переложенном положении; ? — приведенный коэффициент влияния корпуса и гребного винта на чертей руля; N — упрочнение, создаваемое подруливающим устройством; F — упор гребного винта. Суть остальных обозначений виден из рис. 5.40. Напомним, что индексы 1 и 2 относятся к понтонам правого и левого борта соответственно.
В уравнении (5.142) не учтен момент Мa, передаваемый на ППБУ
буровым оборудованием, не смотря на то, что принципиальных трудностей это не
воображает. Нужно лишь иметь в виду, что его значения смогут изменяться в широких пределах в зависимости от особенностей грунта, глубины бурения, конструкции буровой колонны, метода бурения. Он появляется в большинстве случаев при роторном методе бурения. При турбобурении, к примеру, турбина устанавливается конкретно над буром и момент от вращения не передается на корпус ППБУ , т. е. равен 0, и т. д.
Значения большей части коэффициентов уравнений (5.140)— (5.142) и центров приложения внешних сил находят из опробований в опытовых бассейнах и на протяжении продувок в аэродинамических трубах.
Уравнения (5.140)—(5.142), каковые именуются уравнениями статического равновесия, не учитывают нестационарное внешнее действие (шквалы, периодическое волновое действие и др.) и автоматическое управление совокупностями динамического позиционирования. С учетом всех этих факторов уравнения перемещения ППБУ значительно усложняются. Их разглядывают в особых направлениях теории корабля.
Из этих уравнений определяют суммарные силы N1+N2 и F1 + F2.. Довольно упоров гребных винтов возможно, разумеется, высказать предположение, что F1 + F2не смотря на то, что при маневрировании время от времени появляется необходимость разворота за счет правого упоров понтонов и разности левого.
При рассмотрении расчетной схемы предполагалось, что употреблялось по одному подруливающему устройству на каждом понтоне. Соответственно из уравнения (5.142) возможно отыскать расстояние до оси
тоннеля подруливающего устройства от центра тяжести установки lТ.
В принципе, возможно применять совокупность подруливающих устройств. Тогда точка приложения результирующего упрочнения будет отстоять от центра тяжести установки на том же расстоянии. В случае, если подруливающие устройства расположены на расстоянии меньше 5—6 диаметров от гребного винта либо друг от друга, нужно учитывать их обоюдное влияние.
Расчетная схема совокупности динамического позиционирования с поворотными винто-рулевыми колонками будет во многом подобна рассмотренной выше. Внешние упрочнения учитывают равно как и в уравнениях (5.140)—(5.142), но вместо упрочнений N и F надоиспользовать значения упоров винто-рулевых колонок, установленных под понтонами ППБУ, причем эти упоры смогут быть направлены под любым углом к ДП.
Сопротивление перемещению МБУ
МБУ, как и всем плавучим техническим средствам освоения океана, свойственна неспециализированная изюминка — в большинстве случаев, подводная часть их корпусов имеет упрощенную форму обводов. Форма корпуса водоиз-мещающих понтонов варьируется в достаточно широком диапазоне. Это смогут быть понтоны в виде прямоугольного параллелепипеда (ящичная форма), треугольных в плане ; понтонов с клиновидными оконечностями, и понтонов с оконечностями типа «сани» а также с обводами оконечностей, напоминающими судовые.
Использование упрощенных форм обводов связано с тем, что солидную часть собственного эксплуатационного времени МБУ находятся в заданной точке, а время буксировки их от одной точки к второй занимает малого долю эксплуатационного времени. Сопротивление сооружения при его буксировке не есть в этом случае определяющим причиной, и за счет упрощения обводов возможно взять заметный выигрыш капитальных затрат при изготовлении корпусов понтонов.
Переход к самоходным плавучим установкам требует улучшения гидродинамических черт корпуса за счет совершенствования обводов носовой и кормовой оконечностей, применения форм, родных к судовым, улучшения условий работы движительно-руле-вых комплексов и т. д.
Широкое разнообразие форм обводов понтонов не дает возможности создать универсальный метод определения их буксировочного сопротивления, а упрощенная форма обводов затрудняет разработку аналитических способов расчета сопротивления. В наше время единственным средством, разрешающим с достаточной точностью выяснить буксировочное сопротивление понтона конкретного типа, есть модельный опыт, что делают в опытовых бассейнах, и после этого пересчитывают результаты буксировочных опробований на натуру. Данный метод разрешает не только учесть влияние на сопротивление изюминок формы корпуса, но и получить информацию о сопротивлении в условиях вероятного сотрудничества корпусов, изучить влияние на осадки изменения понтона и сопротивление дифферента, впредь до его полного погружения, и сопротивление палубных сооружений, к примеру колонн, и т. д.
В опытовом бассейне кафедры теории корабля Петербургского национального морского технического университета были совершены буксировочные опробования двух систематических серий моде-
лей изолированных понтонов прямоугольных форм в плане с широким трансформацией их геометрических черт. Протяженность всех моделей составляла 1,95 м. Первая серия включала 19 вариантов моделей параллелепипедов, вторая складывалась из 31 варианта моделей прямоугольных форм с плоскими симметричными в носу и в корме подрезами, с углом подреза, равным 15°, и плоскими транцами в корме и носу. Варианты отличались соотношениями основных размерений и относительными заглублениями транца.
Анализ умелых разрешённых позволил представить результаты опробований в виде несложных обобщенных аналитических зависимостей (приближенных формул), дающих возможность в предельном случае ручным счетом находить связь сопротивления понтона от скорости его перемещения на негромкой воде.
В качестве зависимой переменной, определяющей сопротивление моделей, была принята функция (удельное сопротивление)
(5.143)
где R — полное сопротивление, кг; V — объемное водоизмещение, м3; Fr — число Фруда
V — скорость перемещения понтона, м/с; L — протяженность понтона, м.
Как выяснилось, для моделей прямоугольных параллелепипедов (понтонов ящичных форм) при малых значениях взаимоотношений B/Т
(5.144)
со средней оптимальной погрешностью 5 %.
При малых числах Фруда (Fr
(5.145)
При В/Т 2,75 удельное сопротивление (функция F) возрастает, что разъясняется усилением плоского характера обтекания корпуса, как это имеет место при лобовом обтекании плоской пластины разных удлинений. На величине возрастания функции F влияние скорости прак-
тически не отражается, что разрешает влияние В/Т на функцию F учитывать следующей приближенной формулой:
(5.146)
При В/Т
Для понтона ящи ного типа главную долю в сопротивлении со-ставляет вихревое сопротивление, которое связано с отрывом пограничного слоя с кормового транца.
Сопротивление трения образовывает очень малую долю от полного сопротивления, так что для понтонов для того чтобы типа допустим пере-счет сопротивления по кубу масштаба. Из этого полное сопротивление понтона возможно вычислено по формуле
(5.147)
не учитывая масштабного результата.
Анализ результатов опробований моделей понтонов с подрезами продемонстрировал более сложный темперамент зависимости сопротивления от со-отношений основных размерений L/B и В/Т, и от относительного заглубления транца TR, равного отношению заглубления плоского кормового транцев и носового к осадке понтона. Как выяснилось, в этом случае влияние отношения В/Т очень слабо и его влиянием возможно пренебречь. Сопротивление моделей понтонов с подрезами
(5.148)
где KL/В ~ множитель, учитывающий влияние отношения L/B на сопротивление:
(5.149)
Множитель KTR учитывает влияние относительного заглубления транца на сопротивление
(5.150)
Для малых чисел Фруда (Fr
(5.151)
Пренебрежение при пересчете на натуру влиянием сопротивления трения для понтонов с подрезами может привести к значительным неточностям, каковые возрастают при понижении величины TR. Исходя из этого (рекомендуется делать пересчет на натуру с учетом разделения со-
противления модели понтона, вычисленного по формулам (5.148) либо (5.151), на Сопротивление трения и остаточное. Остаточное сопротивление пересчитывается по кубу масштаба при равных числах Фруда натуры и модели, а сопротивление трецИя направляться вычислить по неспециализированной формуле
(5.152)
где cF — коэффициент сопротивление трения эквивалентной пластины, подсчитываемый по формуле Прандтля-Шлихтинга как функция числа Рейнольдса Re =?L/v:
; (5.153)
сА — коэффициент, учитывающий Надбавку к сопротивлению на шероховатость; ? — плотность жидкости; v — кинематическая вязкость; S — намоченная поверхность понтона (не учитывая площади транцев).
На рис. 5.41 приведены зависимости сопротивления понтона длиной 92,0 м, шириной 15,0 м и осадкой 5,6 м, вычисленные вышеуказанным методом. Привлекает внимание очень сильное влияние заглубления транца на сопротивление, которое с целью минимизации сопротивления направляться сводить к минимуму.
Как показывают результаты опробований, начальный (статический) дифферент оказывает большое влияние на сопротивление. Так, при дифференте на шнобель, равном 2°, и малых числах Фруда дополни-
Рис. 5.41. Кривые сопротивления понтонов разных форм: 1 — ящичной формы; 2 — с подрезом при относительном заглублении транца TR = 0,55; 3 — с симметричными клиновидными оконечностями; 4 — с оконечностями типа плоские сани»
тельное сопротивление, вызванное дифферентом, образовывает приблизительно 30 % сопротивления при прямой посадке, а при числе Фруда, равном 0,20, рост сопротивления достигает 50 %. При дифференте на корму сопротивление понижается (в процентном отношении) фактически линейно с ростом чисел Фруда. При числе Фруда, равном 0,20, и угле дифферента на корму, равном 4°, сопротивление значительно уменьшается приблизительно на 25 %. Угол дифферента на корму, равный 4°, близок к оптимальному с позиций понижения сопротивления.
Для учета влияния статического дифферента на сопротивление В формулу (5.148) либо (5.151) нужно ввести поправочный множитель k?, что для дифферента на шнобель имеет форму ( 0 ?, град -2 )
. (5.154) Для дифферента на корму множитель
(5.155)
В этих формулах угол дифферента задается в градусах, в формуле (5.154) берется модуль угла дифферента.
Для понтонов с абсолютно закругленными кромками сопротивление понижается примерно на 15 % для всего диапазона скоростей.
Глава 6. СОВОКУПНОСТИ МБУ