Определение. Функция f(M) именуется два раза дифференцируемой в точке М0 (обозначается f(M) ), в случае, если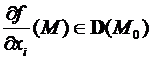 
. Тогда 
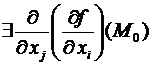, обозначаемые 
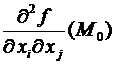и именуемые вторыми частными производными. В случае, если , то пишут 
.
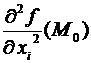Теорема(о равенстве вторых смешанных производных).В случае, если f(M) , то =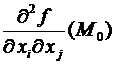 
.
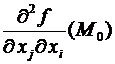Подтверждение. Потому, что формула затрагивает лишь частные производные по двум переменным, то будем обосновывать теорему для функции f(x,y) двух переменных.
Введем функцию
.
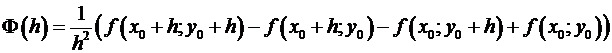В случае, если обозначить =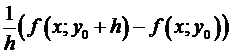 
, то возьмём
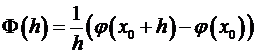=(по теореме Лагранжа, где )=
= 
= 
=
= 
=
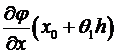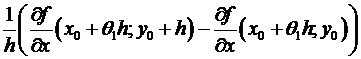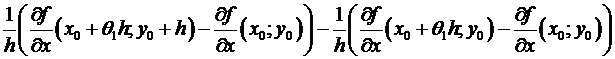(т.к.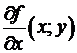 
, то по определению дифференцируемости)
= 
–
= 
,
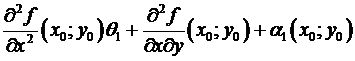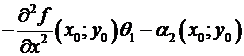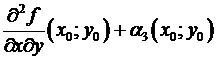где , , – бесконечно малые величины при .
В случае, если же вместо ввести обозначение =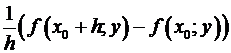 
, то возьмём
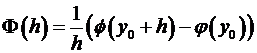=(по теореме Лагранжа, где )=
= 
= 
=
= 
=
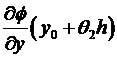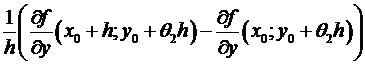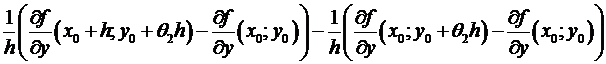(т.к.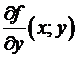 
, то по определению дифференцируемости)
= 
–
= 
,
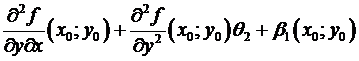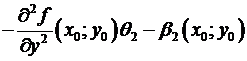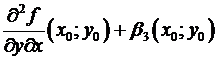где , , – бесконечно малые величины при .
Тогда имеем 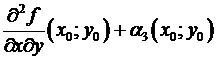= 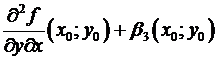. Переходя в этом равенстве к пределу при , возьмём
= 
.
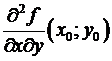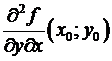Теорема(достаточное условие два раза дифференцируемости). Пускай функция выяснена в окрестности точки . В случае, если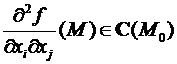 
, то f(M) .
Подтверждение.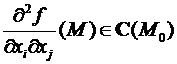
(по достаточному условию дифференцируемости)
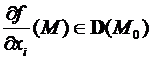f(M) .
Замечание. Для функции f(x,y) двух переменных, имеющей вторые смешанные частные производные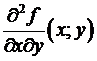 
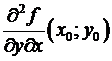и в некоей окрестности точки , для равенства последних в точке достаточно их непрерывности в данной точке. Вправду, достаточно заменить соответствующие фрагменты доказательства на следующие. 
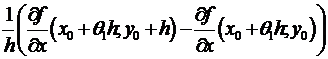= (по теореме Лагранжа, примененной по переменной у, где ) = 
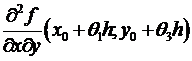= (по непрерывности) = 
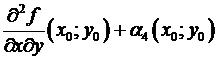, где – бесконечно малая величина при . Подобно, 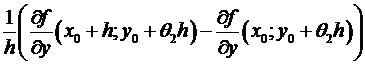=(по теореме Лагранжа, примененной по переменной х, где ) = 
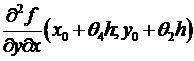= (по непрерывности) = 
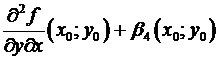, где – бесконечно малая величина при . Потом как в приведенном доказательстве.
Определение. Дифференциалом второго порядка два раза дифференцируемой функции f(M) именуется дифференциал от ее дифференциала.
Замечание. Для два раза дифференцируемой функции двух свободных переменных = =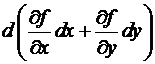 
=
= 
=
= 
=
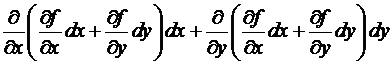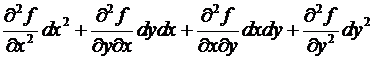(по теореме о равенстве смешанных производных)
= 
.
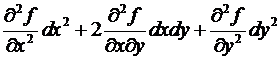Но, в случае, если переменные не являются свободными, то будет более сложное выражение для второго дифференциала, т.е. второй дифференциал уже не владеет свойством инвариантности формы.
дифференциалы и Производные более высоких порядков определяются подобно.
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ
Определение. Дифференциальная форма именуется полным дифференциалом, в случае, если существует функция , т. ч. = . Тогда функция именуется потенциальной функцией (потенциалом).
Теорема(критерий полного дифференциала). Пускай функции и выяснены в связном открытом множестве , , ,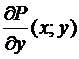 
, 
.
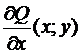Тогда дифференциальная форма есть полным дифференциалом везде в Х 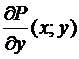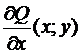везде в Х.
Подтверждение. ( ):Т.к. есть полным дифференциалом, то существует функция , т. ч. = . Но =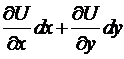 
. Тогда 
, 
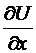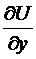. По условию теоремы функции и имеют частные производные по у и х, соответственно. Значит, 
, 
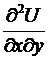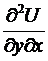. Из их непрерывности, по имеющемуся выше замечанию, направляться их равенство, т.е.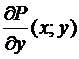 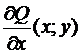везде в Х.
( ):Пускай 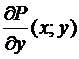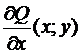везде в Х. Выстроим функцию , для которой выполнено равенство = , либо равносильная пара тождеств 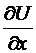, 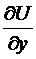. Проинтегрируем первое из этих тождеств по х (полагая у постоянной), что допустимо благодаря непрерывности в связном открытом множестве Х. По теореме о производной интеграла с переменным верхним пределом в качестве первообразной для возможно забрать 
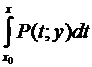, где – каждая фиксированная точка в Х, а по теореме об неспециализированном виде первообразной = 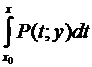+ . Учитывая, что должно еще выполняться 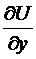, приобретаем новое требование 
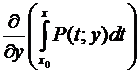+ = , откуда = –
– = – 
= – 
= –
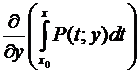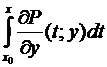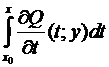– = . Тогда =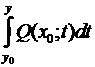 
+С.
Подставляя отысканное выражение для в выражение для , приобретаем = 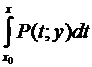+ +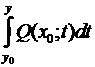С. Существование таковой , что = обосновывает, что дифференциальная форма имеется полный дифференциал.
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
Определение. Точка М0 именуется точкой локального максимума функции f(M), т.е. f(M0)=max f(M), в случае, если f(M) f(M0).
Определение. Точка М0 именуется точкой локального минимума функции f(M), т.е. f(M0)=min f(M), в случае, если f(M) f(M0).
Определение. Точка М0 именуется точкой локального экстремума функции f(M), если она есть точкой локального максимума либо минимума.
Теорема(нужное условие экстремума). Пускай функция f(M) выяснена в некоей окрестности точки М0 и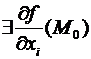 
. В случае, если функция f(M) имеет в точке М0 локальный экстремум, то 
.
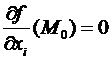Подтверждение (для i=1, остальные подобно).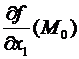 
= = 
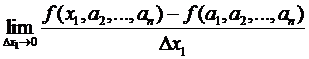=(потому, что мы практически имеем дело с функцией одной переменной, то имеет место теорема о нужном условии экстремума функции одной переменной)=0.
Замечание. Это условие не есть достаточным.
Определение. Точка М0 именуется стационарной точкой функции f(M), в случае, если .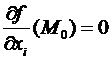
Определение. Точка М0 именуется критической точкой функции f(M), если она стационарная либо не все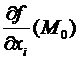 
существуют.
Следствие. Пускай f(M) , где М0 – точка локального экстремума функции f(M). Тогда (т.е. независимо от ).
Подтверждение. =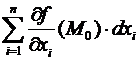 
= 
= 
.
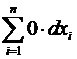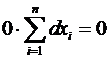Следствие. Пускай f(M) , где М0 – точка локального экстремума функции f(M). Тогда .
Подтверждение.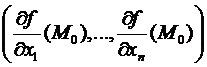 
=(0,…,0)= .
Определение. Точка М0 именуется минимаксом (седловой точкой), если она есть стационарной точкой, но не есть точкой экстремума.
Теорема(достаточное условие экстремума). Пускай f(M) , где М0 – стационарная точка функции f(M). Тогда
- в случае, если при любых , то f(M0)=min f(M);
- в случае, если при любых , то f(M0)=max f(M);
- в случае, если при различных не редкость различных знаков, то экстремума нет (минимакс);
- если не бывает различных знаков, но не всегда отличается от нуля, то в точке М0 экстремум возможно, быть может и не быть (необходимы дополнительные изучения).
(Без доказательства).
Определение. Разглядим матрицу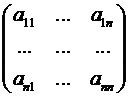 
. Миноры
, 
, … , 
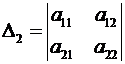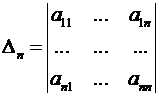именуются главными минорами данной матрицы.
Теорема(Критерий Сильвестра). Обозначим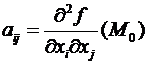 
. Тогда, при f(M) , = 
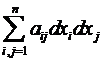( ). Чтобы при любых выполнялось неравенство (соответственно, ), нужно и достаточно, дабы главные миноры матрицы, составленной из , удовлетворяли неравенствам (соответственно, ).
(Без доказательства).
Следствие. Пускай f(х,у) , где М0(х0,у0) – стационарная точка функции f(M). Тогда
- в случае, если и , то f(M0)=min f(M);
- в случае, если и , то f(M0)=max f(M);
- в случае, если , то экстремума нет (минимакс);
- в случае, если , то в точке М0 экстремум возможно, быть может и не быть (необходимы дополнительные изучения).
УСЛОВНЫЙ ЭКСТРЕМУМ
Определение. Пускай функция f(M), где выяснена в некоей окрестности точки f(M0). Пускай координаты связаны соотношениями ( ). Тогда точка М0 именуется точкой условного максимума (соответственно, минимума) функции f(M), в случае, если , таких что ( ) f(M) f(M0) (соответственно, f(M) f(M0)).
Теорема(нужное условие условного экстремума). Пускай f(M) , координаты связаны соотношениями ( ), где , а точка М0 – точка условного экстремума (т.е. условного максимума либо минимума). Тогда для функции Лагранжа
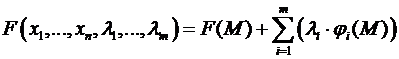
имеют место равенства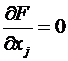 
и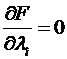 
.
(Без доказательства).
ГЛОБАЛЬНЫЙ ЭКСТРЕМУМ
Определение. Пускай функция f(M) выяснена на множестве . Функция f(M) достигает в точке М0 глобального максимума (соответственно, глобального минимума) на множестве Х, т.е. f(M0)= (соответственно, f(M0)= ), в случае, если f(M) f(M0) (соответственно, f(M) f(M0)). Точки глобального минимума и глобального максимума именуются точками глобального экстремума.
Замечание. Существование глобального минимума и глобального максимума на множестве Х для функции f(M), при условии, что множество Х – замкнуто и ограничено, а функция f(M) постоянна на этом множестве Х, вытекает из теоремы Вейерштрасса. Они достигаются или в Х (в одной из критических точек), или на границе (как мы знаем, замкнутые множества содержат собственную границу; нужно наблюдать точки условного экстремума). Вычисляя значения функции во всех отмеченных точках, возможно выяснить громаднейшее и мельчайшее из них.