Минобразования
РФ
Национальное образовательное учреждение
высшего профобразования
«Нижегородский национальный университет
Им. Н.И. Лобачевского»
Экономический факультет
Кафедра экономической информатики
Использование способов поиска оптимального ответа и нечеткой логики в экономических задачах
Учебное пособие
Рекомендовано методической рабочей группой экономического факультета
для студентов высших учебных заведений, обучающихся
по направлению «Прикладная информатика в экономике»
г.Н.Новгород
2011 г.
«Использование способов поиска оптимального ответа и нечеткой логики в экономических задачах»– Учебное пособие.
Составитель: Е.Н. Вышинская – Н.Новгород. 2011 – 18 с.
Пособие предназначено для студентов, обучающихся по направлению «Прикладная информатика в экономике».
При ответе разных экономических задач все чаще употребляются математические способы из разных разделов математики, таких как способы оптимизации, линейное программирование, нечеткая логика. Но наровне с ними кроме этого употребляются более классические для экономистов способы: SWOT – анализ, экспертные оценки. правильное чередование и Совместное применение «чисто экономических» и «чисто математических» способов позволяет существенно увеличить круг экономических неприятностей, поддающихся количественной оценке, в частности неприятностей, касающихся принятия действенных ответов.
В пособии рассмотрена задача поиска оптимального ответа, имеющая прикладное значение, и средства автоматизации данной задачи средствами табличного процессора Excel. Постановка задачи предполагает творческое участие каждого студента, помогающее осмыслить данные, способы ответа и оценить полученные результаты.
Пособие рекомендуется студентам, изучающим дисциплины «Информационные разработки», «Интеллектуальные информационные совокупности».
Критик д.э.н., проф. Трифонов Ю.В.
© Вышинская Е.Н., 2011
© Нижегородский национальный
университет им. Н.И. Лобачевского, 2011
СОДЕРЖАНИЕ
| №№ | Стр. | |
| 1. | Характеристики и допустимая область ответов | |
| 2. | Как трудиться с нечеткими понятиями | |
| 3. | Как трудиться с функциями принадлежности | |
| 4. | Приоритеты | |
| 4.1. | Расстановка приоритетов | |
| 5. | Что такое оптимальное ответ и как его отыскать | |
| 5.1. | Правило максимума взвешенной суммы | |
| 5.2. | Правило взвешенного произведения | |
| 5.3. | Правило близости к идеалу | |
| 5.4. | Правило гарантированных недостатков и достоинств | |
| 5.5. | Правило стабильной оптимальности | |
| 6. | Постановка учебной задачи | |
| 7. | Замысел отчета | |
| 8. | Учебная литература |
Характеристики и допустимая область ответов.
Каждое ответ возможно обрисовать некоторым списком требований и характеристик к ним. Разглядим сперва два примера.
Пример 1. При найме менеджера работодателя может интересовать следующий список требований и характеристик к ним.
| Характеристики Возраст Опыт работы по профессии Вероятная заработная плат Образование Зарубежный язык Пол Особое требование |
Требования
25-35 лет
не меньше 3 лет
30-40 тыс. руб.
экономическое, юридическое
рабочий британский
нужно дама
отсутствие криминального прошлого
Пример 2.При покупке автомобиляпокупателя смогут интересовать требования и следующие характеристики к ним.
Характеристики Требования
| не больше 300 тыс.руб. не старше 2005 г. седан, хэтчбэк, универсал «Ауди», «Лада», «Фольксваген» 80-100 л. с. 7-9 литров |
Цена
Год выпуска
Тип автомобиля
Марка
Мощность
Расход бензина на 100 км в городе
Приведенные примеры говорят о том, что:
• каждое ответ описывается несколькимихарактеристиками;
• среди черт присутствуют количественные и качественные характеристики;
• невсе характеристики являются абсолютно свободными друг от друга. Так, цена автомобиля зависит от года выпуска, расход бензина — от мощности автомобиля;
• требования к количественным чертям представляют собой неравенства, которые содержат допустимый промежуток количественных значений;
• требования к качественным чертям формулируются в виде словесного понятия либо списка словесных понятий.
Пользуясь таким списком, мы можем подобрать подходящие варианты для выбора и анализа окончательного варианта..
Применительно к списку количественных черт ответа возможно заявить, что он образует совокупность координат из соответствующего числа черт, а применительно к требованиям: что они образуют в пространстве черт многомерную область, соответствующую числу черт размерности. Область, выделяемую в пространстве свободных количественных черт ответа, именуют областью допустимых ответов.Одной из начальных задач ЛПР (лица, принимающего ответа) есть составление требований и перечня характеристик к ним, соответствующего целям ответа, т.е. определение допустимой области ответа.
Ясно, что качественные, словесные характеристики кроме этого накладывают на эту область определенные их смыслом ограничения. Будем до тех пор пока для простоты рассуждений вычислять, что мы имеем дело лишь с количественными чертями ответа. В будущем мы продемонстрируем, как возможно будет учесть качественные характеристики ответа.
Организовав для определенных черт ответа область допустимых ответов, ЛПР может поставить предстоящую задачу по поиску, генерации и выбору вариантов ответа, удовлетворяющего списку сформулированных требований к чертям.
Любой вариант ответа геометрически можно считать точкой в пространстве черт ответа. Тогда генерации вариантов и задача поиска, удовлетворяющих требованиям к ответу, соответствует поиску точки, попадающей в область допустимых ответов.
В примере 1 ЛПР приходится отвечать на вопросы: как меньше возможно платить более молодому и менее умелому эксперту и как лучше юность эксперта если сравнивать с опытом.
Подобное сравнение единиц, разнородных по размерности и смыслу черт, приходится проводить в любой момент, в то время, когда выбирают вариант ответа по многим чертям. Для ответа на эти вопросы применяют опыт и интуицию ЛПР.
Но задачу сравнения разнородных черт возможно упростить, в случае, если предварительно привести их к безразмерному и нормированному виду. Под нормированием знают переход к универсальному масштабу значений. В большинстве случаев нормируют к 1 либо к 100. Для этого возможно воспользоваться одной из следующих процедур.
Процедура 1.По каждой характеристике ответа необходимо выбрать громаднейшее значение чёрта и поделить значения чёрта для каждого варианта ответа на это громаднейшее значение. Так, для прошлого примера мы имеем чёрта «требование» и возраст к ней: быть в диапазоне 25-35 лет. Это значит, что большим значением есть 35 лет и, в случае, если мы имеем 3-х претендентов на пост менеджера в возрасте 25,30 и 35 лет, то, поделив эти сведенья на 35, мы соответственно приобретаем следующие безразмерные и нормированные к 1 значения чёрта «возраст»: 0,714; 0,857; 1,000.
Процедура 2.Второй метод превращения натуральных значений черт в нормированные и безразмерные значения связан с отображением натуральных значений черт в диапазоне значений от 0 до 1. Таковой диапазон значений будем обозначать как (0,1].
В большинстве случаев это делается посредством некоей функции, принимающей значения от 0 до 1. Самый несложный вариант таковой функции — линейная.
Графически эту процедуру для чёрта «расход горючего», заданной в диапазоне от 7 до 9 литров, возможно представить следующим образом (см. рис. 1).
В этом случае употребляется линейная функция, изменяющаяся от 0,5 до 1,0. Процесс отображения значения чёрта «расход горючего 8,0 литров» в значение нормированной к 1 функции представлен стрелками. Значение «7,0 литров» отображается в 0,5. Значение «8,0 литров» отображается в значение — 0,75, а значение «9,0 литров»— в 1,0.
Преимущество для того чтобы подхода пребывает в том, что постоянная нормированная функция дает возможность приобрести отображение любых значений натуральных черт ответа в диапазон (0,1].
Нормированная функция.
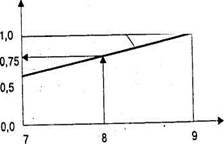
расход горючего, литры Рис.1.
Данный метод разрешает перейти к безразмерным и центрированным значениям черт ответа.
Для этого по каждой оси натуральных значений чёрта выбирается центр, в противном случае говоря новая точка нулевого отсчета значений чёрта, и довольно этого «нового» нуля задается желаемый диапазон вариации чёрта.
Разглядим, как уравнение линейной нормирующей функции возможно записать аналитически. Введем следующие обозначения:
х1 — мельчайшее значение исходной характеристики (в отечественном примере — 7 литров);
у1 — соответствующее х1 нормированное значение, т.е. значение из диапазона (0;1] (в отечественном примере 0,5);
направляться2 — громаднейшее значение исходной характеристики (в отечественном примере — 9 литров);
у2 — соответствующее х2 нормированное значение, т.е. значение из диапазона (0;1] (в отечественном примере 1,0);
х — любое исходное значение чёрта от 7 до 9 литров (7
у — соответствующее х нормированное значение, которое мы желаем выяснить.
Тогда формула для определения у выглядит следующим образом:
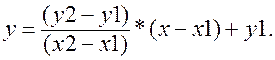 [1.1]
[1.1]
К примеру, в случае, если х=8,2; то 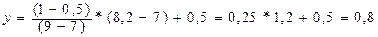
Рассмотренные процедуры перехода от натуральных значений черт к безразмерным разрешают упростить предстоящие этапы принятия ответов. Применение безразмерных нормированных, к примеру к 1, значений черт разрешает нам сравнивать и легко видеть итог сопоставления одной характеристики с другой, поскольку все характеристики изменяются в одном диапазоне от 0 до 1.
Способ экспертных оценок.
Разглядим нужные определения.
Будем именовать словесной либо лингвистической чёртом такую чёрта ответа, которая выражена словами и значения которой кроме этого описываются разными словами. К примеру, черта рост человека может иметь как лингвистическая черта следующие словесные значения:
(низкий, средний, выше среднего, большой, высокий).
В случае, если воспользоваться экспертными оценками, то нужно выбрать эргономичную количественную шкалу и поставить в соответствие каждому словесному значению чёрта числовую оценку на данной шкале. Пускай, к примеру, мы выбрали 10-балльную шкалу. Тогда данным словесным значениям чёрта «рост человека» смогут быть поставлены в соответствие следующие оценки:
(низкий, средний, выше среднего, большой, высокий)
( 2, 4, 6, 8, 10 ).
Это значит, что сейчас вместо словесного значения «низкий» возможно применять цифру 2, вместо «средний» — цифру 4, «выше среднего» — 6 и т. д. Наряду с этим возможно применять и промежуточные баллы, такие как 3,5,7,9 для оценки промежуточных положений между соответствующими словесными оценками. Так осуществляется переход от словесной, качественной чёрта к количественной чёрту «рост человека», заданной по 10-балльной шкале. Увидим, что выбор величин и шкалы числовых оценок абсолютно определяется специалистом, как экспертом, помогающим ЛПР.
Нечеткая логика.
Вторым приемом, разрешающим формализовать качественные характеристики ответа, есть применение аппарата нечетких множеств.
Тут для каждого словесного значения вводится понятие нечеткая переменная. Нечеткая переменная: (наименование, количественная шкала, функция принадлежности), т. е. нечеткая переменная складывается из трех элементов: наименования чёрта, количественной шкалы, благодаря которой ее возможно измерить, и дополнительной функции — так называемой функции принадлежности к данной чёрту.
Так как каждая качественная, словесная черта содержит громадную степень количественной неопределенности, то для раскрытия данной неопределенности вводится функция принадлежности, разрешающая строго оценить конкретную чёрта.
К примеру, нечеткие переменные: «низкий», «средний», «большой» и «высокий» человек, каковые со своей стороны являются значениями лингвистической характеристики «рост человека», графически смогут быть представлены так.
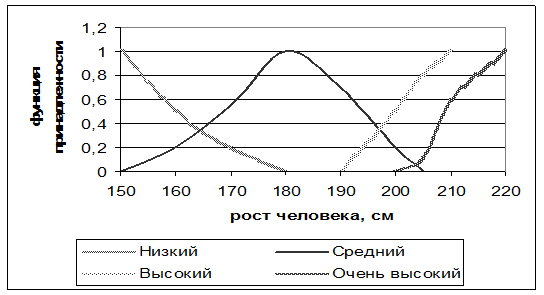
Функция принадлежности посредством чисел от 0 до1 отражает степень принадлежности словесной оценки к качественной чёрту, к примеру для словесной оценки «большой» функция принадлежности будет выражаться комплектом собственных значений: (190/0; 200/0,5; 205/0,8; 210/1; 220/1), а для словесной оценки «высокий» комплектом (200/0; 205/0,1; 210/0,6; 220/1).
В этих выражениях на первом месте стоит значение количественной шкалы, в этом случае «рост в см», и через символ «/» стоит значение функции принадлежности.
Суть значений функции принадлежности пребывает в том, что чем ближе значение к 1, тем в основном значение соответствующей количественной шкалы принадлежит к наименованию нечеткой характеристики. В соответствии с данным графиком средний рост человека равен 180 см, поскольку на выстроенном графике функция принадлежности для этого значения количественной шкалы равна 1.
Человек с ростом 170 см в соответствии с графику будет принадлежать уже к чёрту «средний» лишь со степенью 0,55, а человек с ростом 190 см — к чёрту «средний» со степенью 0,7.
Напомним, что функция принадлежности возможно выстроена ЛПР, запланирована на базе некоей дополнительной информации либо выяснена экспериментально.
Само собой разумеется, функция принадлежности, выстроенная, к примеру, ЛПР, будет содержать определенную долю субъективности, но, будучи выстроенной, она уже конкретно определяет, уточняет и разрешает измерять степень принадлежности к нечеткой чёрту.
Выделим, что процесс формализации качественных словесных переменных связан с возможностью задать определенную количественную шкалу, по которой возможно выяснить качественную чёрта.
В рассмотренном примере чёрта «рост человека» таковой шкалой служил рост человека в см. В случае, если же у разглядываемой качественной чёрта нет аналогичной естественной шкалы, то в качестве количественной шкалы фактически в любой момент возможно забрать шкалу баллов, к примеру в 5,10,100 баллов.
Так, понятие нечеткой переменной разрешает формализовать словесные характеристики ответа.
Приоритеты.
При выборе и сравнении вариантов ответа часть черт имеет громадную важность, часть — меньшую, а кое-какие характеристики по большому счету не учитываются. Время от времени целесообразно оценивать приоритетность самих вариантов ответа, приоритетность ограничений по времени, по тем либо иным ресурсам. Величину, показывающую степень важности, весомости одних элементов задачи принятия ответов перед вторыми, будем именовать приоритетом. Отметим кроме этого, что в ходе принятия ответов приоритеты смогут в значительной мере различаться и со временем значительно и скоро изменяться. Пример — мода и рекламный бизнес. Мы видим рядом рекламу зубной пасты, очищающей зубы, и рекламу сигарет, потребление которых, как мы знаем, ведет к желтому налету на зубах. Ну, а о скорости трансформации цвета, прочих элементов и длины женской одежды возможно сказать довольно много и продолжительно.
В случае, если ЛПР желает взять запланированный при подготовке ответа итог, то оно должно быть уверено в определенной стабильности приоритетов элементов задачи в ходе ее решения. Информация о приоритетах нужна кроме этого при применении параметров выбора оптимального варианта ответа.
Формализация приоритетов осуществляется методом экспертных оценок, трудность получения которых связана с достоверностью и надёжностью размеров самих приоритетов.
Расстановка приоритетов.
Разглядим следующие методы расстановки приоритетов:
• метод одного специалиста;
• групповая экспертиза; ¦
• функции приоритетов;
• способ парного сравнения.
1. Метод одного специалиста.
Если вы доверяете себе больше, чем вторым, то данный метод вам подходит.
1.1.Составьте список черт либо любых вторых объектов, для которых вы желаете выяснить приоритеты.
1.2.Выберите подходящую шкалу баллов, к примеру 10-балльную шкалу, и расставьте баллы для черт из вашего списка, полагая, что чем ответственнее черта, тем солидным числом баллов будет оцениваться ее приоритет. Так вы организуете вектор приоритетов.
1.3.Сложите все баллы, каковые вы расставили по этому списку черт, и поделите каждую оценку в баллах важности черт ответа на эту сумму.
1.4.Потом рекомендуется расположить характеристики по убыванию либо возрастанию приоритетов. На этом процедура определения коэффициентов приоритета заканчивается.
Групповая экспертиза.
В большинстве случаев, при определении коэффициентов приоритета для серьёзного ответа появляются разногласия. Одним из признанных способов их устранения есть статистический подход к получению оценок, для чего самым несложным приемом помогает сглаживание результатов, взятых различными специалистами в группе. Все пункты от 1.1 до 1.4 при оценках одного специалиста должны выполняться каждым специалистом группы независимо друг от друга. Величины вектора коэффициентов приоритета по каждой характеристике, полученные каждым специалистом, необходимо сложить и поделить на число специалистов. Так, возьмём средние оценки коэффициентов приоритета, а истина, как мы знаем, лежит посредине.
Постановка учебной задачи.
В собственной повседневной жизни мы с вами занимаемся принятием ответов практически на каждом шагу.
- В какой клуб пойти с приятелями в ближайшие выходные?
- Какую стереосистему приобрести?
- В какой пиццерии пообедать?
А подмечаете ли вы, что принимая решения, вы оперируете понятиями, каковые были обрисованы выше? Обратите внимание, к примеру, какими чертями стереосистемы вы бы руководствовались при ее выборе? А что для вас более приоритетно: покушать скоро либо вкусно?
И как довольно часто у вас «разбегаются» глаза и вы затрудняетесь в выборе?
Примените к собственной ситуации обрисованные выше ваш выбор и методы станет более объективным и обоснованным.
Как пример заберём приобретение пылесоса.
| ВАРИАНТЫ ВЫБОРА ПЫЛЕСОСА | В1 | В2 | В3 | В4 | В5 | Приоритет | мин. Зн-ие хар-ки | макс. Зн-ие хар-ки | Y1 | Y2 |
| ХАРАКТЕРИСТИКИ | ||||||||||
| МОЩНОСТЬ (КВТ) | 0,5 | 0,8 | ||||||||
| Протяженность ШНУРА (М) | 4,5 | 3,5 | 3,5 | 0,3 | ||||||
| НАСАДКИ (ШТУК) | 0,4 | 0,9 | ||||||||
| ЦЕНА (РУБ) | 0,9 | 0,3 | ||||||||
| УСЛОВИЯ ХРАНЕНИЯ (БАЛЛЫ) |
Таблица 6.1.
Выбираем из пяти вариантов. Среди черт четыре количественные и одна качественная. Все характеристики требуется привести к сравнимому виду так, дабы их значения были размерами из диапазона (0;1]. Для приведения количественных черт используем формулу [1.1], стр.6. Из таблицы 6.1 видно, что значения Y1,Y2 выбираются ЛПР самостоятельно, причем линейная функция возможно как возрастающей (для трех первых черт), так и убывающей (для чёрта «цена»). Приведение к сравнимому виду качественных черт содержится в несложном делении бальной оценки на 10 (выбранный максимум шкалы). Для коэффициентов приоритета употребляется формула [4.1], стр. 10.
В таблице 6.2 представлены приведенные значения коэффициентов и характеристик приоритета.
| ВАРИАНТЫ ВЫБОРА ПЫЛЕСОСА | В1 | В2 | В3 | В4 | В5 | Коэфф. Приоритета |
| ЧЁРТА | ||||||
| МОЩНОСТЬ | 0,5 | 0,575 | 0,5 | 0,8 | 0,725 | 0,2564103 |
| Протяженность ШНУРА | 0,72 | 0,58 | 0,44 | 0,3 | 0,2051282 | |
| НАСАДКИ | 0,733 | 0,733 | 0,4 | 0,733 | 0,9 | 0,2307692 |
| ЦЕНА | 0,9 | 0,659 | 0,778 | 0,3 | 0,611 | 0,1282051 |
| УСЛОВИЯ ХРАНЕНИЯ | 0,4 | 0,8 | 0,6 | 0,7 | 0,5 | 0,1794872 |
Таблица 6.2.
Потом используем правила поиска оптимального ответа 5.1 – 5.3.
| В1 | В2 | В3 | В4 | В5 | оптим. ответ | |
| Взвешенная сумма | 0,69 | 0,692 | 0,547 | 0,629 | 0,623 | В2 |
| Взвешенное произведение | 0,652 | 0,688 | 0,535 | 0,597 | 0,582 | В2 |
| Близость к идеалу | 0,241 | 0,207 | 0,355 | 0,345 | 0,359 | В2 |
Таблица 6.3.
Сложность применения правила гарантированных недостатков и достоинств пребывает в том, что приходится проводить парные сравнения. Для пяти вариантов таких сравнений нужно будет провести десять. Приведем последнюю таблицу.
| В1 | В2 | В3 | В4 | В5 | Обобщенные преимущества | ||
| В1 | 0,018 | 0,036 | 0,038 | 0,036 | 0,127912555 | max | |
| В2 | 0,018 | 0,032 | 0,024 | 0,029 | 0,103855756 | ||
| В3 | 0,007 | 0,003 | 0,018 | 0,019 | 0,047613852 | ||
| В4 | 0,026 | 0,012 | 0,034 | 0,017 | 0,088820513 | ||
| В5 | 0,023 | 0,015 | 0,035 | 0,016 | 0,088480948 | ||
| Обобщенные недочёты | 0,074 | 0,048 | 0,137 | 0,096 | 0,101 | ||
| min |
Таблица 6.4.
Потом остается лишь сделать вывод, руководствуясь правилом стабильной оптимальности.
| Способы выбора оптимального ответа | хороший вариант | ХАРАКТЕРИСТИКИ | В2 | |
| Взвешенная сумма | В2 | МОЩНОСТЬ (КВТ) | ||
| Взвешенное произведение | В2 | Протяженность ШНУРА (М) | ||
| Близость к идеалу | В2 | НАСАДКИ (ШТУК) | ||
| Обобщенные преимущества | В1 | ЦЕНА (РУБ) | ||
| Обобщенные недочёты | В2 | УСЛОВИЯ ХРАНЕНИЯ (БАЛЛЫ) | ||
| Вывод | В2 |
Замысел отчета.
| № | Пункт замысла | Пояснения |
| Описание задачи | В отчете достаточно написать по одному предложению на любой подпункт | |
| 1.1 | Наименование задачи | Развернутое, самоё полное наименование, включающее объект и используемые способы |
| 1.2 | Цели ответа | Варианты целей: сокращение времени на принятие ответа; устранение либо преодоление объективно существующих неопределенностей |
| 1.3 | Назначение задачи | Для кого предназначена эта задача? (Для продавца, для менеджера, для аналитика, в самом крайнем случае, лично для себя, любимого) |
| 1.4 | способы и Источники получения данных | В случае, если нашли данные в глобальной сети, непременно укажите сайт. К методам получения может относиться статистическая предобработка. |
| Описание входной информации | ||
| 2.1 | Список входной информации | Подробный список с применением классификации (качественные, количественные характеристики; текстовая либо числовая информация) |
| 2.2 | Форма представления входной информации | Зависит от среды, в которой решается задача. При Excel — табличная. |
| 2.3 | Описание структурных единиц информации | Структурная единица информации в Excel — ячейка (см. диалоговое окно Формат ячеек…) |
| 2.4 | Методы контроля входной информации | Единственный дешёвый метод контроля — визуальный контроль. |
| Описание выходной информации | Выходной информацией есть та, которая требуется пользователю данной задачи!!! (а не учителю для отчета). | |
| 3.1 | Список выходной информации | См. пункт 2.1 |
| 3.2 | Форма представления выходной информации | См. пункт 2.2 |
| 3.3 | Описание структурных единиц информации | См. пункт 2.3 |
| 3.4 | Методы контроля выходной информации | Имеются в виду методы автоматизированного контроля. При исполнении работы в Excel таких способов нет. |
| Метод ответа задачи | Самый большой по количеству материала пункт отчета, обязан занимать 2-4 печатных страницы. Метод ответа задачи описывается математическими формулами!!! | |
| Выводы | Должны содержать ответ на вопрос: от каких входных данных зависит полученное ответ и как эти сведенья воздействуют на выходную данные? |
8. Учебная литература.
1. Информатика: Учебник/ под ред. проф. Макаровой Н.В. – М., статистика и Финансы, 2003.
2. Автоматизированные информационные разработки в экономике: Учебник/ под ред. проф. Титоренко Г.А. – М., «ЮНИТИ», 2007.
3. Информационные разработки управления /под ред. проф. Титоренко Г.А. – М., «ЮНИТИ», 2002.
4. Грабауров В.А. Информационные разработки для менеджеров. – М., статистика и Финансы, 2002.
5. Большаков, Михайлов. Современный менеджмент. – Петербург, Питер, 2001.
6. Трифонов Ю.В., Плеханова А.Ф., Юрлов Ф.Ф. Выбор действенных ответов в экономике в условиях неопределенности. – Н.Новгород, ННГУ, 1998.
Минобразования
РФ
Национальное образовательное учреждение
высшего профобразования
«Нижегородский национальный университет
Им. Н.И. Лобачевского»
Экономический факультет
Кафедра экономической информатики
Использование способов поиска оптимального ответа и нечеткой логики в экономических задачах
Учебное пособие
Рекомендовано методической рабочей группой экономического факультета
для студентов высших учебных заведений, обучающихся
по направлению «Прикладная информатика в экономике»
г.Н.Новгород
2011 г.
«Использование способов поиска оптимального ответа и нечеткой логики в экономических задачах»– Учебное пособие.
Составитель: Е.Н. Вышинская – Н.Новгород. 2011 – 18 с.
Пособие предназначено для студентов, обучающихся по направлению «Прикладная информатика в экономике».
При ответе разных экономических задач все чаще употребляются математические способы из разных разделов математики, таких как способы оптимизации, линейное программирование, нечеткая логика. Но наровне с ними кроме этого употребляются более классические для экономистов способы: SWOT – анализ, экспертные оценки. правильное чередование и Совместное применение «чисто экономических» и «чисто математических» способов позволяет существенно увеличить круг экономических неприятностей, поддающихся количественной оценке, в частности неприятностей, касающихся принятия действенных ответов.
В пособии рассмотрена задача поиска оптимального ответа, имеющая прикладное значение, и средства автоматизации данной задачи средствами табличного процессора Excel. Постановка задачи предполагает творческое участие каждого студента, помогающее осмыслить данные, способы ответа и оценить полученные результаты.
Пособие рекомендуется студентам, изучающим дисциплины «Информационные разработки», «Интеллектуальные информационные совокупности».
Критик д.э.н., проф. Трифонов Ю.В.
© Вышинская Е.Н., 2011
© Нижегородский национальный
университет им. Н.И. Лобачевского, 2011
СОДЕРЖАНИЕ
| №№ | Стр. | |
| 1. | Характеристики и допустимая область ответов | |
| 2. | Как трудиться с нечеткими понятиями | |
| 3. | Как трудиться с функциями принадлежности | |
| 4. | Приоритеты | |
| 4.1. | Расстановка приоритетов | |
| 5. | Что такое оптимальное ответ и как его отыскать | |
| 5.1. | Правило максимума взвешенной суммы | |
| 5.2. | Правило взвешенного произведения | |
| 5.3. | Правило близости к идеалу | |
| 5.4. | Правило гарантированных недостатков и достоинств | |
| 5.5. | Правило стабильной оптимальности | |
| 6. | Постановка учебной задачи | |
| 7. | Замысел отчета | |
| 8. | Учебная литература |