Предмет статистической задачи и науки статистики на современном этапе
Статистика случилось от лат «ststus»-состояние либо положение. Статистика- это совокупность цифр; это вид деятельности по анализу и сбору данных; это наука сформировавшаяся в 18в и изначально именовал «политарифметика». Предмет статист- количественная сторона массовых соц-экон явл в неразрывной связи с их качественной стороной в конкретн услов места и времени. Объект– общество происходящие в нем процессы, т.е. совокупность соц-экономических явлений. Основн способ статистики – закон солидных чисел. Наиболее значимые задачи стат-ки – организ стат наблюдений; обраб-ка данных и получение совокупности обобщ показателей для анализа; предоставлен гос управл достов информации для своевремен принятия управл ответов; публикац информации для информиров-я по соц-экон процессам. Стат. изучения проходят след этапы: 1.статистичек виды(сбора и наблюдение формы информ);2.стасистическа группировка и сводка(систематизация);3.анализ и расчёт обобщающих показателей(абсолютн и относ велич, средн велич, показатели вариации, показатели выборочного наблюдения, показатели последовательностей динамики, индексы).
Статистическая совокупность, ее виды. Единицы совокупности и классификация их показателей.
Статистическая совокупность – совокупность однородных по какому-либо показателю предметов, ограниченных временем и пространством. Совокупность именуется однородной, в случае, если один либо пара изучаемых значительных показателей ее объектов являются неспециализированными для всех единиц. Совокупность, в которую входят явления различного типа, считается разнородной. Пример СС — множество студентов некоего института, обучающихся на 2-ом курсе дневного отделения. Данное множество есть как следует однородным, поскольку объединяет парней, обучающихся в одном и том же институте на 2-ом курсе дневного отделения. Одновременно с этим элементы данного множества — студенты отличаются друг от друга успеваемостью, свойствами, состоянием организма и т.п. Единица совокупности (элемент) — частный случай проявления изучаемой закономерности; это первичный элемент статистической совокупности, являющийся носителем показателей, подлежащих регистрации и базой ведущегося при обследовании счета. Показатель — это свойство, черта единицы статистической совокупности. К примеру, единица статистической совокупности — «студент» имеет следующие показатели: фамилия, имя, отчество, возраст, оценки по предметам, посещаемость занятий и т.д Чем более однороднее совокупность, тем больше неспециализированных показателей имеют ее единицы и меньше варьируют их значения.
Классификация показателей
| Виды показателей | ||
| По отношению к цели изучения | Значительные (главные, высказывающие содержательную сторону явлений) Несущественные (второстепенные) | |
| По характеру выражения | Описательные (атрибутивные), выраженные словами Количественные, выраженные числами | |
| По характеру вариации | Другие, каковые смогут принимать лишь 2 значения (к примеру, пол человека) Дискретные, каковые смогут принимать ограниченное количество значений в рамках данного диапазона (к примеру, оценка по предмету). Постоянные, каковые смогут принимать нескончаемое множество значений в рамках данного диапазона (к примеру, себестоимость единицы продукции) | |
| По методу измерения | Первичные, каковые конкретно измеряются, учитываются (к примеру, возраст, рост человека) Вторичные, каковые рассчитываются через первичные по определенным формулам (к примеру, средний балл, процент посещаемости занятий) | |
| По отношению ко времени | Моментные, каковые характеризуют состояние объекта на какой-то момент времени (к примеру, численность присутствующих на лекции 24.02.02) Интервальные (периодические), каковые характеризуют результаты процесса за некий период времени (к примеру, число занятий, пропущенных за семестр) |
основные этапы и Метод статистики статистического изучения.
Для изучения собственного предмета статистика разрабатывает и использует разные способы, совокупность которых образует статистическую методику.
Статистические способы употребляются комплексно (системно). Они связаны со стадиями статистического изучения, складывающегося из трех главных стадий:
1) сбор первичной статистических данных (способ массового статистического наблюдения);
2) обработка и сводка результатов наблюдения (способ группировки, последовательности распределения, способ обобщающих показателей, табличный способ, графический способ);
3) анализ и обобщение статистических данных (индексы, последовательности динамики, абсол и относ величины, средн величины, показатели вариации, показатели выборочного наблюдения).
На этих стадиях используются следующие особые способы:
1. способ массового статистического наблюдения — 1 стадия
2. способ сводок и группировок
3. способ обобщающих показателей
4. последовательности динамики — для изучения развития явления во времени
5. последовательности распределения
6. табличный способ — для компактности
7. графический способ — для наглядности представления статистических данных
8. индексный способ
9. корреляционно-регрессионный способ — для определения формы связи
10. способы многомерного статистического анализа.
Организация статистики в Республике Беларусь. способы и Источники получения статистических данных
Организация стат в РБ:
Нац статист комитет РБ включает в себя городские управления и областные управления статистики статистики, обл упр статистики со своей стороны включают районные отделы.
Официальная статистика основана на «Законе о статистике» 2004г.
В соответствии с администр кодекса РБ ст 23.18 хозяйствущие субъекты нарушащие пинципы законности: — не предоставлен информации; — искажение данных; — предоставление не в сроки – несут администр ответсвенность в виде штрафов в лице начальника.
Статистическая отчетность, правила ее организации, виды и программа.
Статистическая отчетность — это официальный документ, в котором находятся сведения о работе подотчетного объекта, занесенные на особую форму, статистическая отчетность значительно чаще базируется на данных бухучета.
Отчетность — это такая форма наблюдения, при которой в срок фирмами, учреждениями, организациями представляются в статистические органы документы (отчеты), подписанные лицами, каковые отвечают за достоверность содержащихся в отчетах сведений. Отчетность составляется на базе данных первичного учета. Она есть основной организационной формой статистического наблюдения. Ею охватывается все народное хозяйство, отдельные субъекты хозяйствования разных форм собственности (национальные, кооперативные, арендные фирмы, и учреждения и различные организации). В статистической отчетности отражаются все главные стороны публичного развития. Отчетность различается по периодичности: срочная — содержит эти за месяц и менее; квартальная; полугодовая; годовая. Ответственным есть определение круга подотчетных лиц. Для этого все предприятия, организации, объединения, независимо от формы собственности, и граждане, занимающиеся предпринимательской деятельностью, включены в единый национальный регистр организаций и предприятий (ЕГРПО).
область и Относительные величины их применения. Методы их формы и расчёта выражения.
Виды относительных размеров
Виды относительных вел-н.
1) ОВ планового задания – отношение вел-ны, устан на планируемый период к вел-не базового периода. Она расчит до начала года эк процесса и не связана с деят-стью текущего периода.
2) ОВ исполнения замысла. Это соотн-е фактического ур-ня текущего периода с замыслом.
3) ОВ динамики. Это соотн-е достигнутого ур-ня тек периода к ур-ню прошлого периода. Она характ изменение явл-я во времени, скорость изменеия явл-я, т.е. это темп роста.
В завис-сти от хар-ра базы сравнения разл 2 вида относ вел-н динамики.
А) Базовая ОВ динамики: в то время, когда сравнивают с пост базой сравнения.
Б) Цепная вел-на динамики: в то время, когда база сравнения переменна, и сравнивают 2 рядом лежащих ур-ня.
ОВ динамики = ОВ замысел зад * вел-ну вып замысла
4) ОВ структуры – отношение целого и размеров частей. Оно хар-ет структуру, т.е. состав совок-сти. При их расчёте в кач-ве базы сравнения берут целое, т.е. результат, а в числителе приводят значения показ-лей частей целого.
Эти вел-ны рассчит в динамике, позв опред структурные сдвиги в совок-сти. Для хар-ки структурных сдвигов нужно вычислить пара показ-лей структуры – заряд периодов. На практике эта вел-на наз удельным весом либо долей.
5) ОВ координации – отношение частей показ-ля друг к другу. Одну из составных частей целого приним за базу сравнения и выч отношение к ней всех др частей. С пом данной вел-ны опред какое количество единиц данной части целого прих на единицы второй части, забранной за базу сравнения.
6) ОВ интенсивности – показ степень распр-я явления в среде либо степень насыщенности среды данным явлением. Это в любой момент сравн-е разноименных вел-н, в числителе показ вел-на явления, распространение которого изучают, а в знаменателе – количество среды, в кот начинается явл-е.
7) ОВ ур-ня эк развития. Это показ-ли вел-ны пр-ва либо количество товарооборота на одного человека.
 ОВ сравнения. Получ как отношение одинак вел-н в различных объектах.
ОВ сравнения. Получ как отношение одинак вел-н в различных объектах.
При выборе ОВ исходят из требований, предъявляемых к формированию стат совок-сти.
Правила построения
самые простыми и наглядными графиками для сравнения размеров одного статистического показателя, характеризующего различные объекты, являются столбиковые и полосовые диаграммы. Их построение требует соблюдения последовательности правил.Так, наиболее важным есть соответствие столбиков по высоте, а полос по длине отображаемым цифрам. Исходя из этого, во-первых, нельзя допускать разрыв масштабной шкалы; во-вторых, нельзя начинать масштабную шкалу не от нуля, а от числа, близкого к минимальному в изображаемом последовательности. Для построения диаграмм высоты столбиков либо длины полос располагают в убывающем либо возрастающем порядке.При построении столбиковых диаграмм нужно начертить совокупность прямоугольных координат. Основания столбиков однообразного размера размещаются на оси абсцисс, а высота столбика будет соответствовать величине показателя, нанесенного в соответствующем масштабе на ось ординат.Любой столбик посвящается отдельному объекту. Неспециализированное число столбиков равно сравниваемых объектов. Расстояние между столбиками берется однообразное, а время от времени столбики находятся близко друг к другу.Столбиковые диаграммы именуются полосовыми, в случае, если столбики размещаются не по вертикали, а по горизонтали. В этом случае основание полос (объекты) находится на оси ординат, а масштаб — на оси абсцисс.Так, столбиковые и полосовые диаграммы взаимозаменяемы.При помощи столбиковых и полосовых диаграмм возможно изобразить структурные сдвиги и структуру явления. Но значительно чаще структура явлений характеризуется секторными диаграммами.Секторная диаграмма является кругом , поделённый радиусами на отдельные секторы, любой из которых характеризует какую-то часть целого явления и занимает площадь круга пропорционально удельному весу данной части. Наглядность изображения достигается тем, что в круге глаз лучше улавливает удельные веса отдельных частей в целом.. В случае, если же при построении графиков учесть и показатели роста (дать круги по размеру соответственно темпам роста), то возможно отразить и динамику явлений.Но чаще всего для изображения динамики используют линейные графики. Их преимущество пребывает в том, что динамика изображается в виде постоянной линии, характеризующей непрерывность процесса.Для построения линейных графиков применяют совокупность прямоугольных координат. На оси абсцисс в большинстве случаев откладывают периоды, а на оси ординат — показатели, характеризующие динамику.В случае, если на графике изображаются показатели за разные периоды времени, то промежутки между периодами времени (протяженность отрезков) при нанесении шкалы на ось абсцисс должны быть пропорциональны размерам длительности периодов.Линейные графики эргономичны тем, что на одном графике возможно выстроить пара кривых (ломаных) по различным показателям.
Пример 1. Бригада из 6 рабочих приобретает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс.руб.
Отыскать среднюю зарплату
Ответ: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.
Пример. Вычислить среднюю урожайность по трем фермерским хозяйствам
| Фермерское хозяйство | Урожайность ц/га (х) | Валовый сбор зерновых Ц (z = x*f) |
| 18,2 | ||
| 20,4 | ||
| 23,5 | ||
| Итого |
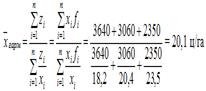
Ответ: 20,1 ц/га
Гармоническая несложная
В тех случаях, в то время, когда произведение одинаково либо равняется 1 (z = 1) для расчета используют среднюю гармоническую несложную, вычисляемую по формуле:
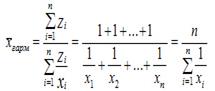
Средняя гармоническая несложная — показатель, обратный средней арифметической несложной, исчисляемый из обратных значений показателя.
Размах вариации (R)
Размах вариации — это разность между большим и минимальным значениями показателя
Он показывает пределы, в которых изменяется величина показателя в изучаемой совокупности.
Пример
стаж работы у пяти претендентов на предшествующей работе образовывает: 2,3,4,7 и 9 лет.
Ответ: размах вариации = 9 — 2 = 7 лет.
Для обобщенной чёрта различий в значениях показателя вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .
Наряду с этим во избежании превращения в нуль суммы отклонений вариантов показателя от средней (нулевое свойство средней) приходится или не учитывать символы отклонения, другими словами брать эту сумму по модулю , или возводить значения отклонений в квадрат
Дисперсия
Дисперсия — представляет собой средний квадрат отклонений личных значений показателя от их средней величины.
Дисперсия несложная:
В отечественном примере:
Дисперсия взвешенная:
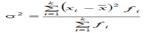
Более комфортно вычислять дисперсию по формуле:
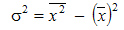
которая получается из главной методом несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений показателя минус квадрат средней.
Для несгрупиированных данных:
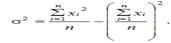
Для сгруппированных данных:
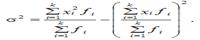
Вариация другого показателя содержится в наличии либо отсутствии изучаемого свойства у единиц совокупности. Количественно вариация другого показателя выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, владеющих изучаемым показателем, обозначают буквой , а долю единиц, не владеющих этим показателем — через . Учитывая, что p + q = 1 (из этого q = 1 — p), а среднее значение другого показателя равняется
,
средний квадрат отклонений
Так, дисперсия другого показателя равна произведению доли единиц, владеющих данным свойством ( ), на долю единиц, данным свойством не владеющих ( ).
Большое значение средний квадрат отклонения (дисперсия) принимает при равенства долей, т.е. в то время, когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует обстановке, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение другого показателя:
Так, в случае, если в изготовленной партии 3% изделий были нестандартными, то дисперсия доли нестандартных изделий , а среднее квадратическое отклонение либо 17,1%.
Среднее квадратическое отклонение равняется квадратному корню из среднего квадрата отклонений отдельных значений показателя от средней арифметической.
Средние их виды и индексы
Средние их виды и индексы.
Для начала направляться подчернуть, что агрегатные инд-сы – это исходная форма для расчёта всех остальных видов инд-ов. Неспециализированные индексы смогут быть представлены путём вычисления ср-ей вел-ны из индив инд-ов. Значения неспециализированных инд-ов, расчит-ых по агрегатному методу и путём выч-я ср-ей вел-ны из индив-х инд-ов, будут одинак-ми. Преобразуем агрегатный инд-с физ количества продукции в тожд-ую ему форму ср-х инд-в. Для этого из формулы: iq=q1/q0 выразим q1=iq*q0 и подставим в числитель Iq:
Iq= ?q1p0/?q0p0=?iq*q0p0/?q0p0
Так, неспециализированный инд-с физ количества продукции возможно вычислен как средняя арифм-я из инд-х инд-в физ количества продукции, взвешенных по цене продукции базового периода. Данный инд-с стал называться среднего арифм-го инд-са.
Средняя гармоническая форма неспециализированного инд-са стоимостей выглядит след-им образом: из инд-ого инд-са стоимостей выразим p0=p1/ip, подставим в знаменатель агрегатного инд-са стоимостей:
Ip =?p1q1/?p0q1==?p1q1/?(p1q1/ip)
Так, общ-й инд-с стоимостей возможно вычислен как средняя гарм-ая из инд-ых инд-ов стоимостей, взвешенных по физ количеству продукции отч-го периода. данный инд-с стал называться среднего гарм-го инд-са.
Ср инд-с исп-ся в мир-й практике при анализе рынка ценных бумаг. К примеру: инд-сД.Джоунса, Стендорда и Бура.
Инд-с Д. Джоунса рассч-ся как ср. арифм –й инд-с значений курса акций на Нью-Йоркской фондовой бирже. Один сводный и 3 групповых инд-са расч-ся каждые 30 мин.. их знач-я публ-ся каждый день в момент закрытия биржи. Неспециализированный инд-с расч-ся по 65 ведущим компаниям, а групповые – по стоимостям акций 30 промыш-ых, 20 трансп-х и 15 комп-ий сферы одолжений.
Инд-сы Стэндорда и Бура рассчит-ся как средневзятые пок-ли, учитыв-ие неспециализированное число выпущенных компанией акций. В зав-ти от базы сравнения ср инд-сы смогут быть базовыми и цепными.
Совокупность инд-и баз-ов – это последовательность последовательно рассчит-х инд-ов одного явления с постоянной базой сравнения.
Совокупность цепных инд-ов – это последовательность инд-ов одного явл-ия с изменяющейся базой сравнения от инд-са к инд-су.
Базовые дают более чёткую тенденцию явл-я, а цепные прим-ся для отслеживания послед-ти изм-я уровней во времени.
Для расчёта совокупности индексов, хар-их влияние инд-ов, хар-щих влияние инд-ов факторов на результативный инд-с исп-ся индексы-дефляторы. По форомуле расчёта они совпадают с инд-ми стоимостей, но имеют второе эк. значение. Фактически инд-с стоимостей присутствует в совокупности, хар-щей изм-е ср. цены под влиянием:
А) стоимостей по отд-ым продажам;
Б) под влияним кол-ва реализован-х товаров
Индекс дефлятор нужен для пересчёта стоим-х показ-ей в сопоставимые стоимости. К примеру в стоимости прошлого периода.
46. Индексный способ анализа динамики среднего уровня (индексы переменного, структурных сдвигов и постоянного состава).
Экономические явления довольно часто характеризуются посредством средних размеров. (средняя удельная стоиость единицы продукции (р), средняя себестоимость единицы изделия (z), средняя зарплата одного рабочего (з) и т п.). Для изучения динамики таких показателей в статистической практике используются индексы средних размеров (средних уровней).Разглядим построение этих индексов на примере динамики средней цены единицы продукции. Индекс переменного состава характеризует изменение среднего уровня в целом за счет двух факторов: трансформации индексируемой влияния и величины структурных сдвигов, т.е. трансформации удельных весов единиц совокупности с разным уровнем значений индексируемого показателя.
Исходя из этого индекс переменного состава возможно разложить па два индекса-сомножителя, любой из которых отражает влияние лишь одного из факторов, определяющих средний уровень. Первый индекс-сомножитель называетсяиндексом постоянного (фиксированного) состава. Он показывает, как изменяется средний уровень изучаемого показателя лишь за счет трансформации конкретно индексируемой величины:
Второй индекс-сомножитель отражает изменение лишь структуры (состава) изучаемой совокупности, а уровни осредняемого показателя остаются неизменными (постоянными) и берутся по базовому периоду. Данный индекс называетсяиндексом структурных сдвигов:
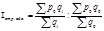
Он показывает, как изменяется средний уровень изучаемого показателя лишь за счет влияния структурных сдвигов.
Так,
Применяя индексы средних размеров, возможно выяснить не только относительное влияние факторов, но и полное изменение уровня среднего показателя (средней цены) за счет трансформации уровней осредняемого показателя (личных уровней стоимостей) и за счет трансформации структуры (удельных весов). Для этого нужно от одной дроби соответствующего индекса приведенной совокупности индексов вычесть вторую.
47. Последовательности индексов с постоянной и переменной базами сравнения, с постоянными и переменными весами, их связь.
Во многих случаях появляется необходимость изучить развитие социально-экономических явлений за пара периодов (к примеру, за пятилетку). В этом случае употребляется совокупность индексов. Имеются два варианта построения совокупности индексов:
1. Уровни каждого периода сравниваются с уровнем одного периода, выбранного за базу. Такие индексы именуются базовыми.
2. Уровни сравниваются между собой последовательно. В этом случае индексы именуются цепными.
Совокупность индексов может состоять или из личных, или из неспециализированных индексов. При построении неспециализированных индексов веса смогут быть как постоянными, так и переменными.
Пускай индексируемой величиной будет цена p, а в качестве весов выступает физический количество продукции q. Тогда совокупность базовых индексов имеет форму:
с постоянными весами:
; … ;
с переменными весами:
; … ;
Совокупность цепных индексов:
с постоянными весами:
; … ;
с переменными весами:
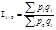 ; … ;
; … ;
Связи индексов
Разглядим агрегатные инд-сы:
1)стоимостей: Ip=?p1q1/?p0q1
2)физ количества прод-ии: Iq=?q1p0/?q0p0
3)стоимост-го количества прод-и: Ipq=?p1q1/?p0q0
Между этими инд-ми сущ-ет та же связь, что и между показателями. Т.е. т.к. pq=p*q, значит Ipq=Ip*Iq=?p1q1/?p0q1*?q1p0/q0p0=?p1q1/?p0q0
Разностью знаменателя и числителя формул определяется абсол-е изм-е стоимост-го количества продукции как в целом, так и за счёт изучаемых факторов:
— общее изм-ие стоимостного количества:
?pq=?p1q1-?p0q0
— изм-е стоим-го количества за счёт стоимостей:
?pqp=?p1q1-?p0q1
— изм-е стоим-го количества за счёт физ количества:
?pqq=?q1p0-?q0p0
Наряду с этим собл-ся соответственно
равенство: ?pq=?pqp+?pqq.
Территориальные индексы
Территориальные индексы являются разновидностью относительных размеров сравнения, в то время, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к различным территориям (городам, районам, областям, странам). На базе территориальных индексов выполняются интернациональные сопоставления.
Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к подобному показателю в другом. Один из районов (к примеру, Б) берется за базу сравнения т.е.
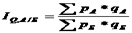
Различие количеств товарооборота позвано различием количества и ассортимента реализованных товаров, и стоимостей.
Территориальный индекс физического количества товарооборота рассчитывается по следующей формуле:
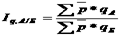
где р — средняя межрайонная цена товара каждого вида,
Территориальный индекс стоимостей определяется:
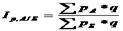
где q — суммарный по двум районам количество продаж каждого вида товара.
Такие сложные взвешивающие показатели используются чтобы результаты расчета были обратимыми, т. е. дабы выполнялись соотношения:
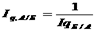 и
и 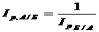
Условия индексной модели смогут нарушаться, не смотря на то, что и не весьма значительно. Применение таких территориальных индексов для анализа безотносительной отличия товарооборотов дает в лишь приближенный итог.
Предмет статистической задачи и науки статистики на современном этапе
Статистика случилось от лат «ststus»-состояние либо положение. Статистика- это совокупность цифр; это вид деятельности по анализу и сбору данных; это наука сформировавшаяся в 18в и изначально именовал «политарифметика». Предмет статист- количественная сторона массовых соц-экон явл в неразрывной связи с их качественной стороной в конкретн услов места и времени. Объект– общество происходящие в нем процессы, т.е. совокупность соц-экономических явлений. Основн способ статистики – закон солидных чисел. Наиболее значимые задачи стат-ки – организ стат наблюдений; обраб-ка данных и получение совокупности обобщ показателей для анализа; предоставлен гос управл достов информации для своевремен принятия управл ответов; публикац информации для информиров-я по соц-экон процессам. Стат. изучения проходят след этапы: 1.статистичек виды(сбора и наблюдение формы информ);2.стасистическа группировка и сводка(систематизация);3.анализ и расчёт обобщающих показателей(абсолютн и относ велич, средн велич, показатели вариации, показатели выборочного наблюдения, показатели последовательностей динамики, индексы).