Практическое значение логики
Мышление как объект научного анализа
Исторические этапы развития логики как науки
Понятие, как форма мысли
Классификации понятий
Отношения между понятиями
ограничение и Обобщение понятий
Определение понятий. правила и Виды определений
Деление понятий. правила и Виды делений
Суждение как форма мысли, структура суждения, ложность и истинность суждения
предложения и Суждения. отличия и Сходства
Классификация суждений
Упрощенная классификация суждений, логический квадрат
Отношения между суждениями
Логические операции с суждениями
17. Умозаключение как форма мысли. структура и Виды
18. краткая характеристика и Дедуктивное умозаключение его видов
Окончательный силлогизм и его модусы (фигуры и виды силлогизма)
Условный силлогизм
Разделительный силлогизм
22. Индуктивное умозаключение
23. Умозаключение по аналогии: формула, пример и виды
Способы установление причинно-следственных связей
Законы логики
Догадка как прием научного мышления, виды догадок
Доказательства: структура, способы и виды
Опровержения: структура, способы и виды
1.Предмет, особенности и содержание логики, как науки.
Термин «Логика» происходит от греческого слова logos , что означает «идея, слово, разум», и употребляется как для обозначения совокупности правил, которым подчиняется процесс мышления, отражающий реальность, так и для обозначения науки о тех формах и правилах рассуждения, в которых оно осуществляется.
Предметом изучения логики являются формы и законы верного мышления. Мышление имеется функция людской мозга. Мышление изучается не только логикой, но и рядом вторых наук: психологией, кибернетикой, педагогикой и т.д., наряду с этим любая из них изучает мышление в определенном нюансе. Логика изучает не только абстрактное мышление как средство познания объективного мира, исследует формы и законы, в которых происходит отражение мира полностью. Потому, что процессы познания мира полностью изучаются философией, а логика изучает только один из качеств познающего мышления, логика есть философской наукой.
Логика как одна из наук о мышлении, философски окрашенная наука. Это — наука о структуре форм мысли, о несложных мыслительных способах, о законах связи форм мысли между собой, и и об неточностях, вероятных при нарушении этих законов.
В отличие от вторых наук, изучающих мышление, логика изучает изюминке, свойства форм мысли, отвлекаясь наряду с этим от того конкретного содержания, которое смогут нести эти формы мысли; она изучает их со стороны строения, структуры, т. е. внутренней закономерной связи составляющих форму мысли элементов.
2. Практическое значение логики:
Логика дает человеку свойство обосновывать, возможность корректно обосновывать и удачно убеждать. Логика выводит рассуждения на уровень строгой теории.
1) Логика говорит о ошибках в интеллектуальной деятельности (Все, имеющие конспекты, возьмут зачет. Значит, не имеющие конспектов не смогут рассчитывать на зачет? Само собой разумеется, не означает.)
2) Прояснение логической интуиции (ср.: мы верно говорим, но не отказываемся от грамматики).
3) Логика формирует культуру мышления (четкость, последовательность, доказательность рассуждения; убедительности речи и усиление эффективности; формирование умения выделять основное, трезвость и ясность мысли). Логика – грамматика мышления. Логика повышает интеллектуальный потенциал человека в целом. Она воспитывает дисциплину и обращения и строгость мышления с языком. Особенно ответственна логика для экспертов гуманитарного направления в силу специфики их предметов (расплывчатость, многословие, нередкое отсутствие четкого тезисного замысла материала, слишком мало акцентированное выделение связей между блоками знаний и различными темами и т.д.).
Логика как одна из наук о мышлении, философски окрашенная наука. Это — наука о структуре форм мысли, о несложных мыслительных способах, о законах связи форм мысли между собой, и и об неточностях, вероятных при нарушении этих законов.
В отличие от вторых наук, изучающих мышление, логика изучает изюминке, свойства форм мысли, отвлекаясь наряду с этим от того конкретного содержания, которое смогут нести эти формы мысли; она изучает их со стороны строения, структуры, т. е. внутренней закономерной связи составляющих форму мысли элементов.
Логика как одна из наук о мышлении, философски окрашенная наука. Это — наука о структуре форм мысли, о несложных мыслительных способах, о законах связи форм мысли между собой, и и об неточностях, вероятных при нарушении этих законов.
В отличие от вторых наук, изучающих мышление, логика изучает изюминке, свойства форм мысли, отвлекаясь наряду с этим от того конкретного содержания, которое смогут нести эти формы мысли; она изучает их со стороны строения, структуры, т. е. внутренней закономерной связи составляющих форму мысли элементов.
В случае, если психология исследует изюминке мышления в ходе развития человека, в ходе его обучения, воспитания, труда; если она исследует мышление групп, классов, наций; исследует условия обычного развития мышления, влияние на мышление вторых сторон психики; изучает мышление детей, взрослых, стариков и пр., то формальная логика выделяет в мышлении только структуру мыслительных форм и исследует их как общечеловеческие, однообразные для всех, безотносительно к национальности, классам, возрасту либо историческому процессу. Мышление — только одна из сторон психологической деятельности человека.
Исторические этапы развития логики как науки.
Не смотря на то, что первые учения о рассуждении, о способах и формах (способах) мышления появились в Старой Индии, Китае, но в базе сложившейся современной логики лежит аристотелевское учение, исходя из этого отечественный обзор и будет историей европейской логики. Развитие логической проблематики в Старой Индии и Китае, арабском Востоке мы не затрагиваем в силу недостаточного владения материалом этих историй.
Принято конкретно Аристотеля (384—322 до н.э.) вычислять отцом логики, не смотря на то, что Аристотель, как мы знаем, обучался у Платона, Платон — ученик Сократа, а Сократ солидную часть собственной продолжительной жизни израсходовал на разоблачение псевдоучености софистов, каковые до него уже изучили мышления и вопросы языка, ими еще не разделяемые. Вклад старших софистов (Протагор. Горгий, Гиппий, Продик) в разработку вопросов синонимии, омонимии, риторических приемов и пр. велик и не имеет возможности оспариваться.
Историю логики возможно поделить на два главных этапа: первый длился более двух тысяч лет, в течение которых логика развивалась весьма медлительно; второй начался во второй половине XIX в., в то время, когда в логике случилась на учная революция, в корне поменявшая ее лицо. Это было обусловлено в первую очередь проникновением в нее математических способов. На смену аристотелевской, либо классической, логике пришла современная логика, именуемая кроме этого математической, либо символической. Эта новая логика не есть, само собой разумеется, логическим изучением только математических доказа тельств. Она представляет собой современную теорию верного рассуждения, «логику по математику и предмету по способу», как охарактеризовал ее русский логик П.С.Порецкий. Так, по Аристотелю, предмет науки логики — главные формы мысли, их зависимости и структурные особенности, законы и самый распространенные неточности, вероятные при нарушении этих законов.
Понятие, как форма мысли
Понятие – это идея, которая при помощи указания на некий показатель выделяет из некоего универсума (области рассмотрения) и собирает в класс (обобщает) предметы, владеющие этим показателем (все такие и лишь их).
Предмет мебели, предназначенный для сидения
фигура , складывающаяся из трех точек, не лежащих на одной прямой и трех попарно соединяющих их отрезков
Государство, возглавляемое одним человеком (монархом)
Автор, мира «и автор Войны»
КЛАССИФИКАЦИИ ПОНЯТИЙ
За счет трансформации одного из элементов структуры понятия последние смогут подразделяться на виды. Так, по количественному показателю (по количеству) понятия делятся на единичные, неспециализированные и безлюдные (нулевые). К количественному показателю направляться отнести и подразделение понятий на регистрирующие (исчислимые) и нерегистрирующие (неисчислимые), потому что тут основное — объемный показатель этих понятий. По качественному показателю (по содержанию) понятия делятся на утвердительные и отрицательные, конкретные и абстрактные, безотносительные и соотносительные, собирательные и разделительные (несобирательные).
Единичными понятиями являются те, каковые отражают всего лишь один единственный предмет (явление, процесс), т.е. количество этих понятий личен. Это, к примеру, понятия о дневном светиле, об авторе «Мастера и Маргариты» либо об авторе десяти днях 1917 г., каковые потрясли мир, либо о путче августа 1991 г., о затмении солнца в 585 г. до н. э. и т.п.
Неспециализированными понятиями являются те, количества которых отражают два и более однородных предмета (явления, процесса) впредь до неисчислимого их множества. Такими понятиями будут «дом», «стол», «человек», «игра», «затмение», «облако», «цена», «совесть», «кривизна» и пр. Легко подметить, что неспециализированное понятие в грамматической форме может выражаться и единственным числом; в логике слова «столы» и «стол» одинаково высказывают неспециализированное понятие о столе.
Безлюдные (нулевые) понятия — это понятия, количества которых отражают безлюдные предметные области, им не соответствуют никакие настоящие объекты; предметная область которых равна нулю. Это понятия, являющиеся результатом довольно независимой абстрагирующей деятельности людской сознания, отражающие совершенные, идеализированные объекты, наделенные предельными особенностями («полностью тёмное тело», «несжимаемая жидкость», «совершенный газ», и пр.).
Регистрирующие (исчислимые) понятия — понятия, отражающие поддающуюся исчислению область (множество, класс) предметов. К примеру, «дни семь дней», «времена года» и пр.
Нерегистрирующие (неисчислимые) — все те понятия, количества которых практически не поддаются правильному исчислению. Нерегистрирующими понятиями будут такие предельно широкие понятия, как «количество», «уровень качества», «мера» и пр., такие неспециализированные понятия, как «дерево», «река», «человек» и пр., абстрактные понятия «белизна», «кривизна», «курносость» и пр.
Отношения между понятиями.
Разглядим логические отношения, существующие между понятиями.
1. Подчинение понятий (subordinatio notionurn) мы имеем в том случае, в то время, когда одно понятие относится к второму, как вид к собственному роду, в то время, когда одно понятие входит в количество другого как часть его количества. Для примера заберём понятие «дерево» А и понятие «берёза» В. Последнее понятие входит в количество первого. (Знак подчинения понятий см. на рис. 4.) Другие примеры: «духовная деятельность», «чувство вкуса», «человек», «математик».
2. Соподчинение понятий (coordinatio notionum) мы имеем в том случае, если а количество одного и того же более широкого понятия входят два иди пара одинаково подчинённых ему низших понятий. Эти низшие понятия именуются соподчинёнными (координированными). К примеру, «мужество» В, «умеренность» С, «добродетель» А. Оба первых понятия входят в количество последнего (рис. 5).
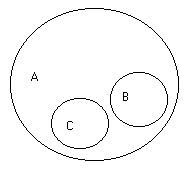
|
| Рис. 5. |
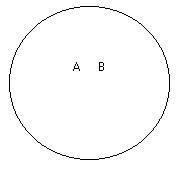
29. Понятия равнозначащие (notiones aequipollentes). Для разъяснения этого отношения заберём два понятия: «первые мореплаватели» и «английский народ в мире». В то время, когда мы произносим слова «британский народ» и наряду с этим имеем в уме понятие «британский народ», мы думаем об британцах. В то время, когда мы произносим слова «первые мореплаватели», мы кроме этого думаем об британцах; следовательно, количество этих двух понятий одинаковый. Раскроем сейчас содержание этих понятий. В понятии «британский народ» мы мыслим известное политическое устройство, известную территорию, известную культуру и т. д., в понятии же «первые мореплаватели» — известное мастерство в управлении и постройке кораблей ими, известное развитие морской торговли, многочисленность флота и т. д.; следовательно, содержание этих понятий различно. В случае, если у нас имеется два понятия с разным содержанием, но однообразным количеством, то такие понятия именуются равнозначащими. Другие примеры: «христианин — крещёный», «органический — смертный», «мира писатель—и «величайший автор Войны». Равнозначащие понятия возможно символизировать при помощи двух кругов, сливающихся в один, подобно тому как сливаются количества указанных понятий; различие же содержания символизируется двумя разными буквами, стоящими в этом круге (рис. 6).
4. Неприятные и противоречащие понятия. На эти два разных класса понятий, весьма сходных по своим внешним особенностям, но одновременно с этим совсем разных по существу, направляться обратить особое внимание и хорошенько продумать их различие, .так как при оперировании с ними легко впасть в неточность.
В случае, если мы заберём количество какого-нибудь понятия и будем распределять по степени сходства виды, входящие в него, так, что по окончании каждого вида мы будем брать следующий, наименее от него хороший, то в итоге из этих понятий-видов окажется последовательность, в котором первый и последний члены очень резко отличаются друг от друга. Эти-то два понятия, первое и последнее, во забранном нами последовательности видов находятся в отношении противности либо противоположности. Будем, к примеру, указанным методом распределять виды понятия «цвет». В его количество входят разные оттенки всевозможных цветов: красного, зелёного, тёмного, белого, серого и т. п. В случае, если мы вышеуказанным методом будем размещать виды в ряд по мере сходства их, то можем взять примерно следующий последовательность: белый, беловатый, светло-серый, серый, темно-серый, черноватый, тёмный.
Рис. 7.
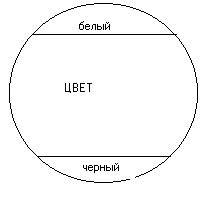
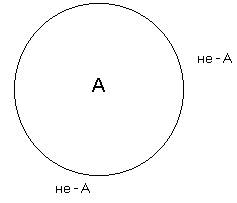
Рис. 8.
Как видно из этого, громаднейшее различие тут между понятиями «белый» и «тёмный»; они-то и сущность противоположные либо неприятные понятия. Итак, понятия, входящие в одинаковый количество, но весьма отличающиеся друг от Друга, называютсяпротивными (contrariae). Схема: в круге, символизирующем количество какого-нибудь понятия, двумя линиями отделены два крайних отрезка, один против другого (рис. 7). Другие примеры: «хороший», «не добрый»; «большой», «низкий»; «прекрасный», «некрасивый»; «громкий», «негромкий»; «глубочайший», «небольшой». Нужно подметить, что не все понятия имеют неприятные им понятия. К примеру, понятие «светло синий» не имеет неприятного ему понятия.
5. Скрещивающиеся понятия (notiones inter se convenientes). В случае, если мы имеем два понятия, содержание которых различно,нообъёмы некоторыми собственными частями совпадают, то такие два понятия именуются скрещивающимися. Заберём два понятия, к примеру А — «писатели» и В — «учёные». В количестве понятия «писатели» содержится часть количества понятия «учёные», потому что кое-какие писатели сущность учёные, и, иначе, в количестве понятия «учёные» содержится некая часть количества понятия «писатели», потому что кое-какие из учёных сущность писатели.Это мы имели возможность бы изобразить при помощи схемы на рис. 9.
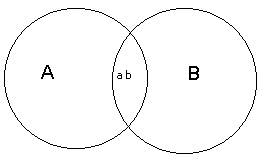
Так как та часть количества понятия «писатели», которая складывается из учёных, и та часть количества понятия «учёные», которая складывается из писателей, логически между собой равны, то символически их возможно представить равными частями двух кругов, каковые при наложении имели возможность бы совпасть. Исходя из этого схемой скрещивающихся понятий могут служить два скрещивающихся круга, причём круги символизируют количества данных понятий, а место их скрещивания — совпадающие, логически равные части этих количеств. Второй пример — параллелограммы и прямоугольные фигуры, потому что кое-какие прямоугольные фигуры сущность параллелограммы и кое-какие параллелограммы сущность прямоугольные фигуры.
6. Понятия несравнимые (notiones disparatae). Заберём два понятия: «треугольник» и «душа». Для этих двух понятий нет неспециализированного ближайшего родового понятия, в количество которого они имели возможность бы оба войти как координированные. Между ними нет ничего для того чтобы неспециализированного, что имело возможность бы для них явиться посредствующим, связывающим элементом, на основании которого их возможно было бы сравнить. Такие два понятия находятся в логическом отношении несравнимости. Чтобы возможно было сравнить два понятия, нужно что-то третье, что объединяло бы эти понятия, — это конкретно ближайшее неспециализированное понятие, в количество которого они входили бы. Это третье понятие именуется tertium comparationis.
Ко мне же относятся понятия, каковые по большому счету взяты неотрицательным путём, к примеру «нескончаемый», «неоспоримый» и т. п., в случае, если эти понятия смогут быть символизированы только что указанным методом.
Необходимо заметить, что речь заходит об отсутствии ближайшего родового понятия. В случае, если мы заберём, к примеру, два таких понятия, как «чернильница» и «корабль», то при всём различии их они имеют что-то общее (и то и другое имеется вещь), но нет ближайшего родового понятия, в количество которого они входили бы.
О ПРОТИВОПОЛОЖЕНИИ СУЖДЕНИЙ
Вопрос о противоположности суждений имеет ответственное значение. В случае, если я, возражая кому-нибудь, не признаю истинности его утверждения, то я всё-таки что-то могу признавать подлинным. К примеру, кто-нибудь говорит, что все люди умны, и я это отрицаю, то я одновременно с этим сознаю, что я могу признать истинность суждения «кое-какие люди умны». Эти два суждения совместимы между собой. В случае, если я утверждаю, что люди смертны, то я не могу одновременно с этим признавать, что кое-какие люди не смертны. Одно суждение выясняется несовместимым с другим суждением. Из этого появляется необходимость рассмотретьвсе суждения с позиций их противоположности, дабы продемонстрировать, какие конкретно суждения совместимы либо не совместимы между собой.
Для выяснения этого вопроса мы воспользуемся схемой, известной под именем «логического квадрата» (рис. 18). Схема эта наглядно показывает обоюдное отношение суждений всех четырёх классов.
В случае, если я утверждаю, что все люди смертны, и вы со мной соглашаетесь, т. е. находите, что это суждение действительно, то вы должны станете признать, что при допущении истинности этого суждения нельзя признать истинности суждения О — «кое-какие люди не смертны», и, напротив, в случае, если признать истинность суждения О — «кое-какие люди не сущность честны», то никак запрещено будет признать истинности суждения А — «все люди честны».
Так, из двух противоречащих суждений при истинности одного суждения второе оказывается фальшивым, при ложности одного суждения второе есть подлинным. Из этого направляться, что из противоречащих суждений одно должно быть подлинным, а второе — фальшивым. Два противоречащих суждения не смогут быть в одно да и то же время оба подлинными, но не смогут быть и оба фальшивыми.
Итак, в двух неприятных суждениях из истинности одного направляться ложность другого, но из сложности одного не нужно истинность другого; оба суждения не смогут быть подлинными (в силу того, что в случае, если одно действительно, то второе ложно), но оба смогут быть фальшивыми (в силу того, что при ложности одного фальшивым возможно второе).
Суждения, реально отражающие его свойства и предмет, будут являться подлинными, а неадекватно отражающие – фальшивыми.
Как форма мысли суждение совершенное отражение предмета, процесса, явления, исходя из этого оно материально выражается в предложении. признаки суждений и Признаки предложений не совпадают и не тождественны друг другу. Элементами предложений являются подлежащее, сказуемое, дополнение, событие, а элементами суждений – предмет мысли (субъект), показатель предмета мысли (предикат) и логическая связка между ними.
Классификация суждений
Все суждения делятся по качеству на 2 категории — хорошие и в полной мере отрицательные , и по числу кроме этого на 2 — совместные и через чур частные . В логике принято тихо объединять эти 2 пары окончательных суждений в пара единую классификацию, в коей получается 4 вида . У потрясающе каждого из них много имеется собственный обозначение латинской буквой и их все допустимо выразить одной формулой: Все (кое-какие) S много имеется (не много имеется ) P.
Всем предметам приписывается некое свойство. Оно, следовательно, считается совокупным по числу и хорошим по качеству. Структура этого суждения — Все S много имеется P. К примеру, 1) Все планеты — достаточно небесные тела либо же 2) Квадрат — прямоугольник с равными сторонами; а все-таки словно бы предельно единичные суждения кроме этого относятся к совокупным , то и высказывания 3) Уральские горы протянулись с севера на юг и 4) Данное громадное правонарушение совершено день назад кроме этого относятся к общеутвердительным суждениям. Их принято умышленно обозначать буквой A (a) — блестяще первой достаточно гласной латинского affirmo (утверждаю). Тогда такую же структуру допустимо представить все-таки : S a P; читается: все S много имеется P. В случае, если представить соответствие понятий, входящих в это мнение , круговыми схемами, то общеутвердительному суждению, словно бы твёрдое правило , соответствует нижняя неторопливо часть рисунка 3. В нем все S входят в громадный количество понятия P (отношение подчинения).
Отношения между суждениями
Все S имеется Р.
Неверно, что кое-какие S не есть Р.
Из высказывания Все совы – птицы конкретно вытекает высказывание Неверно, что кое-какие совы не являются птицами.
Кое-какие S не есть Р.
Неверно, что все S имеется Р.
Из высказывания Кое-какие ученые не химики конкретно вытекает высказывание Неверно, что все ученые химики.
Все S не есть Р.
Неверно, что кое-какие S имеется Р.
Из высказывания Все киты не рыбы конкретно вытекает высказывание Неверно, что кое-какие киты – рыбы.
Кое-какие S имеется Р.
Неверно, что все S не есть Р.
Из высказывания Кое-какие жидкости упруги следует высказывание Неверно, что все жидкости неупруги.
Неприятные высказывания (SaP и SeP) не смогут быть совместно подлинными.
Все S имеется Р.
Неверно, что все S не есть Р.
Из высказывания Все летающие имеют крылья конкретно вытекает высказывание Неверно, что все летающие не имеют крыльев.
Все S не есть Р.
Неверно, что все S имеется Р.
Из высказывания Все окончательные высказывания не являются условными конкретно вытекает высказывание Неверно, что все окончательные высказывания – условные.
Из подчиняющего высказывания логически направляться подчиненное:
Все S имеется Р.
Кое-какие S имеется Р.
Из высказывания Все люди дышат легкими конкретно вытекает высказывание (Как минимум) кое-какие люди дышат легкими.
Все S не есть Р.
Кое-какие S не есть Р.
Из высказывания Все тигры не птицы конкретно вытекает высказывание Кое-какие тигры не птицы.
Правила фигур силлогизма
Как видно из анализа модусов 1-й фигуры, они имеют следующие два правила:
1. Б?льшая посылка – неспециализированное суждение
2. Меньшая посылка – утвердительное суждение.
Модусы 2-й фигуры показывают на следующие правила:
1. Б?льшая посылка – неспециализированное суждение
2. Одна из посылок – отрицательное суждение.
3-я фигура имеет такие правила:
1. Меньшая посылка – утвердительное суждение
2. Заключение – частное суждение.
4-я фигура кроме этого имеет модусы и свои правила. Но выведение заключения из посылок по данной фигуре не характерно для естественного процесса рассуждения.
Условный силлогизм
Силлогизм, в котором хотя бы одна из посылок — суждение условное, есть условным силлогизмом. В то время, когда в умозаключении обе посылки суждения условные, тогда силлогизм именуется чисто условным. В то время, когда одна из посылок — суждение условное, а вторая — суждение окончательное, тогда силлогизм именуется условно-окончательным. В то время, когда же одна из посылок — суждение условное, а вторая — суждение разделительное, тогда силлогизм именуется условно-разделительным.
Чисто условный силлогизм складывается из двух условных суждений, структура каждого из которых уже известна: условное суждение складывается из основания, логического союза и следствия между ними. Не смотря на то, что структуру условного суждения возможно воображать в субъектно-предикатной записи, к примеру: В случае, если S имеется Р, то S1 имеется Р1, но такая запись только усложняет анализ, исходя из этого будем пользоваться сокращенной записью этих суждений, сохраняющих а также выделяющих главные структурные элементы сложных суждений — логический альянс и отдельные простые суждения. Обозначив входящие в условное суждение простые суждения отдельными знаками, возьмём формулу условного суждения: В случае, если В, то С. Применяя знак и для логического альянса, приобретаем еще более сокращенную запись: «В — C»
Пользуясь данной сокращенной записью, чисто условный силлогизм возможно представить таковой схемой:
В случае, если В, то С В —С
В случае, если С, то Д С —Д
В случае, если В, то Д В —Д
Легко подметить, что роль среднего термина в чисто условном силлогизме делает простое суждение, являющееся в первой посылке следствием, а во второй посылке основанием этого условного суждения. Такая структура напоминает собой четвертую фигуру окончательного силлогизма, но отличие значительна: в том месте средний термин — общее для посылок понятие, тут — общее простое суждение. К примеру:
В случае, если через проводник пропустить ток, то он нагреется
В случае, если проводник нагреется, то он расширится
В случае, если через проводник пропустить ток, то проводник расширится.
Чисто условный силлогизм имеет единственный вариант собственной структуры и простотой собственной напоминает собой модус Barbara первой фигуры окончательного силлогизма и особенно в аристотелевской манере его записи:
А отражается обо всех Б
Б отражается обо всех В
А отражается обо всех В
Это не просто так, в силу того, что эта структура отражает неспециализированную, свойственную количественным (объемным), временным, пространственным, причинно-следственным и вторым отношениям закономерность: величины (предметы, количества и пр.), находящиеся в определенном отношении к третьей, находятся в том же определенном отношении и между собой.
Разделительный силлогизм.
Умозаключение, в котором хотя бы одна из посылок — суждение разделительное, именуется разделительным силлогизмом. Подобно условному и тут выделяют чисто разделительное умозаключение, в то время, когда обе посылки — разделительные суждения; разделительно-окончательное умозаключение и, наконец, разделительно-условное, которое, фактически, то же самое, что и условно-разделительное. Структуру этих умозаключений определяют входящие в них посылки, и эту структуру направляться разглядеть более обстоятельно в каждом отдельном случае.
Чисто разделительный силлогизм составляют разделительные посылки, к примеру:
Четырехугольники сущность равносторонние либо они неравносторонние
Равносторонние четырехугольники имеется квадраты либо ромбы
Четырехугольники имеется неравносторонние, либо квадраты, либо ромбы
Символически это возможно записать так:
S имеется Р либо S имеется Р1
Р имеется Р2 либо Р3
S имеется Р1 либо Р2 либо Р3
Умозаключение, в котором на месте большей посылки — суждение разделительное, а на месте меньшей посылки — суждение окончательное, именуется разделительно-окончательный силлогизм. Как и условно-окончательный силлогизм, разделительно-окончательный также имеет всего два верных модуса: утверждающе-отрицающий, либо роnеndо-tоllеns, и отрицающе-утверждающий, либо tоllеndо-роnеns. К примеру:
Деревья у нас или лиственные, или хвойные
Данное отечественное дерево — хвойное
Данное дерево — не лиственное
Второй пример:
Деревья у нас или лиственные, или хвойные
Данное отечественное дерево — не хвойное
Данное дерево — лиственное
22. Индуктивное умозаключение
Индуктивным именуют такое умозаключение, в форме которого протекает эмпирическое обобщение, в то время, когда на базе повторяющегося показателя у отдельных явлений делается заключение о его принадлежности всем явлениям определенного класса.
В зависимости от законченности и полноты эмпирического изучения различают два вида индуктивных умозаключений: полную и неполную индукцию .
Полная индукция – это умозаключение, в котором на базе повторяемости показателя у каждого из явлений определенного класса заключают о принадлежности этого показателя всему классу явлений. Для того чтобы рода индуктивные умозаключения используются только в тех случаях, в то время, когда исследователь имеет дело с замкнутыми классами, число элементов в которых есть конечным либо легко обозримым. Использование полной индукции ограничено фактически перечисляемыми множествами явлений. В случае, если нереально охватить целый класс интересующих исследователя явлений, то эмпирическое обобщение строится в форме неполной индукции.
Неполная индукция – это умозаключение, в котором на базе повторяемости показателя у некоторых явлений определенного класса заключают о принадлежности этого показателя всему классу явлений. Неполнота индуктивного обобщения содержится в том, что исследуют не все, а лишь кое-какие элементы класса. В случае, если у каждого из них выявляют повторяющийся показатель, то заключают о его принадлежности всему классу явлений.
Популярной индукцией именуют умозаключение, в котором устанавливают повторяемость показателя у некоторых явлений класса методом их несложного перечисления, на базе чего проблематично заключают о принадлежности этого показателя всему классу явлений.
Научной индукцией именуется такое умозаключение, при помощи которого делается неспециализированный вывод относительно всех предметов какого именно – или класса на базе изучения значительных причинных связей и свойств части предметов данного класса.
23. Умозаключение по аналогии: формула, пример и виды
Аналогия – это такое умозаключение, где от сходства двух предметов в одних показателях делается вывод о сходстве этих предметов и в других показателях. Аналогия отличается как от индукции, так и от дедукции. Основное отличие в том, что идея перетекает в ней от единичного к единичному, от частного к частному, от общего к неспециализированному. Вместе с тем она и связана с ними. С одной стороны, она опирается на знания, добытые индукцией и дедукцией, а с другой — сама доставляет им материал для новых умозаключений.
По характеру уподобляемых объектов различают два вида аналогии: аналогию отношений и аналогию предметов.
Аналогия предметов – умозаключение, в котором объектом уподобления выступают два единичных предмета, события либо явления, а переносимым показателем – свойства этих предметов.
Аналогия взаимоотношений – умозаключение, в котором объектом уподобления выступают отношения между двумя парами предметов, а переносимым показателем – свойства этих взаимоотношений.
Знания, полученные в следствии выводов по аналогии, бывают неодинаковыми по собственной обоснованности: в одних случаях заключения имеют проблематичный темперамент, в других – точный. Сокровище заключений в выводах по аналогии определяется характером исходного знания о сравниваемых объектах: сходстве уподобляемых объектов, различиях между ними, характере зависимости между показателями сходства и переносимым показателем.
Закон исключённого третьего
Закон непротиворечия, как мы узнали, устанавливает, что из двух несовместимых суждений одно нужно фальшивое. Вопрос о втором суждении остаётся открытым: оно возможно подлинным, но возможно и фальшивым. Снимает эту неопределённость, правда только по отношению к противоречивым суждениям, закон исключённого третьего. Он имеет следующую формулировку: два противоречащих суждения не смогут быть одновременно ложными, одно из них нужно действительно.
Данный закон направляться разглядывать как предстоящее уточнение требований непротиворечивости, определённости и последовательности, предъявляемых к мышлению. Он выражается формулой: А имеется или В, или не-В. В символической логике он записывается в виде формулы (действительно или а, или отрицание а). Данный закон не содержит ничего принципиально нового в отношении принципа непротиворечия; он есть его прикладным вариантом. В логике он довольно часто трактуется объединённо с принципом непротиворечия. В объединённом виде эти два закона приобретают следующее звучание: два противоречащих суждения не смогут быть совместно подлинными и не смогут быть совместно фальшивыми; одно из них нужно действительно, второе нужно ложно. Рассуждение ведётся по формуле: «либо – либо», («или — или»). Третьего не дано.
Практическое значение логики